人教版三年级下册数学课件-第8单元数学广角—搭配(共93张PPT)
文档属性
| 名称 | 人教版三年级下册数学课件-第8单元数学广角—搭配(共93张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 15:10:49 | ||
图片预览








文档简介
(共93张PPT)
部编人教版三年级数学下册
第8单元数学广角—搭配
【全单元】
PPT课件
组
数
数学广角—搭配(二)
8
他们都是谁?
孙悟空这个角色更深入人心,深受大家喜爱,当唐僧将他从五指山救出之后,给他取名叫“孙行者”。
《西游记》改编自明代小说家吴承恩同名文学古典名著,是中国文学史上一部最杰出的充满奇思异想的神魔小说。
下面三个字可以有多少种不同的组合?
孙
行
者
同桌交流:把所有可能都写下来,然后举手回答。
孙行者
行孙者
者行孙
孙者行
行者孙
者孙行
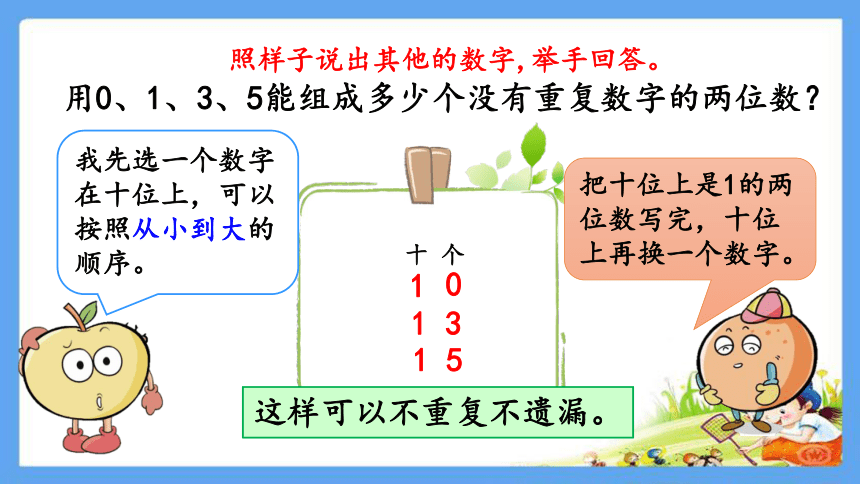
用0、1、3、5能组成多少个没有重复数字的两位数?
0
1
5
3
十位上不能是0。
小组交流:写下所有你能想到的数字。
十
个
把十位上是1的两位数写完,十位上再换一个数字。
1
0
1
3
1
5
这样可以不重复不遗漏。
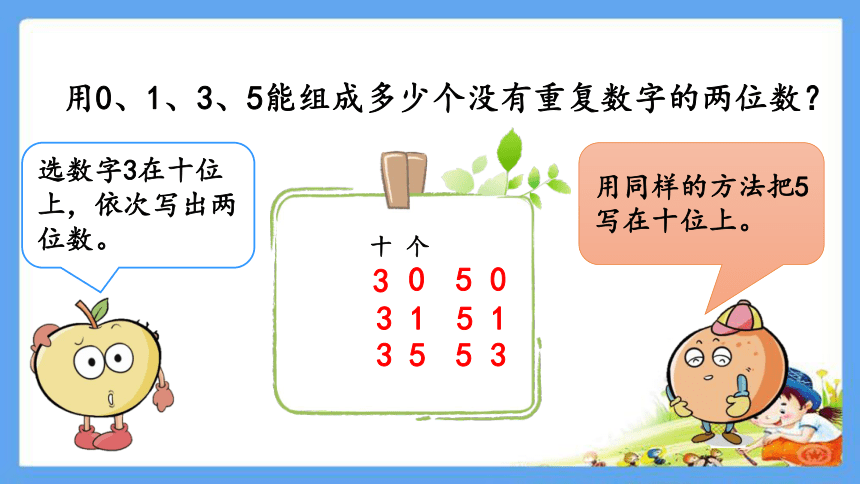
用0、1、3、5能组成多少个没有重复数字的两位数?
我先选一个数字在十位上,可以按照从小到大的顺序。
照样子说出其他的数字,举手回答。
十
个
用同样的方法把5写在十位上。
3
0
3
1
3
5
5
0
5
1
5
3
选数字3在十位上,依次写出两位数。
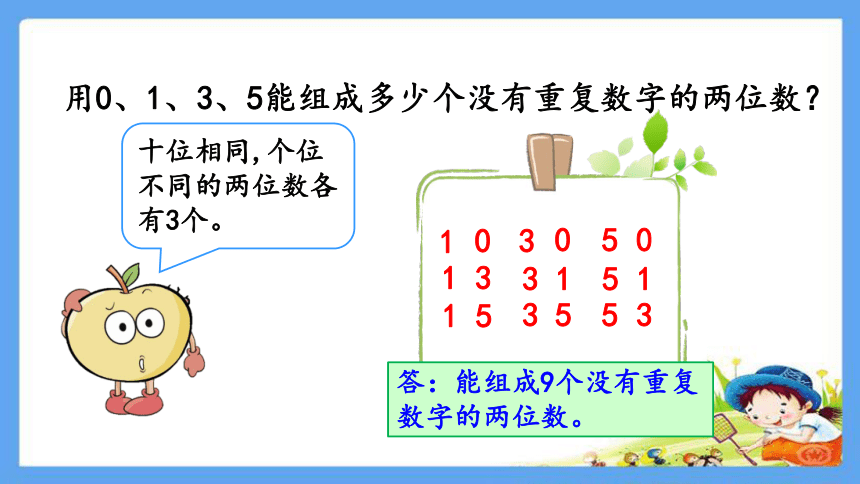
用0、1、3、5能组成多少个没有重复数字的两位数?
3
0
3
1
3
5
5
0
5
1
5
3
1
0
1
3
1
5
答:能组成9个没有重复数字的两位数。
十位相同,个位不同的两位数各有3个。
用0、1、3、5能组成多少个没有重复数字的两位数?
用2、4、6、8能组成多少个没有重复数字的两位数?
注意:按照一定顺序排列。
4
2
6
2
8
十
个
2
十
个
2
4
6
4
8
4
十
个
2
6
4
6
8
6
十
个
2
8
4
8
6
8
十位相同,个位不同的两位数各有3个,所以一共能组成12个两位数。
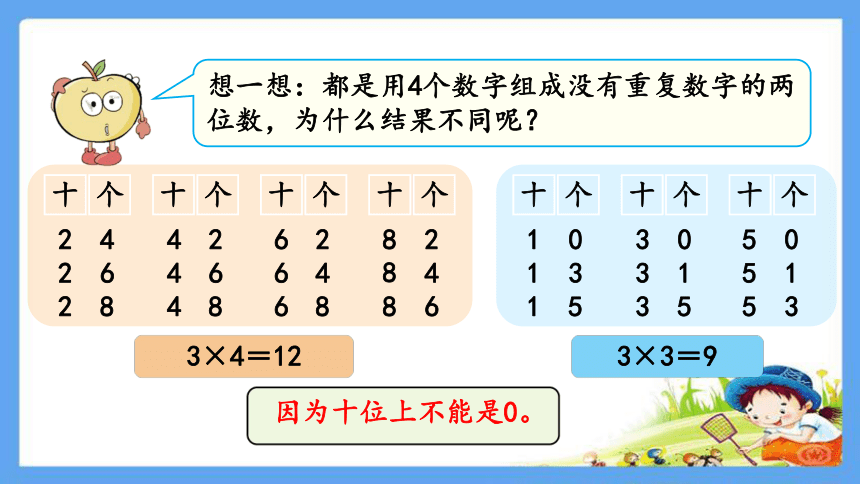
想一想:都是用4个数字组成没有重复数字的两位数,为什么结果不同呢?
4
2
6
2
8
十
个
2
十
个
2
4
6
4
8
4
十
个
2
6
4
6
8
6
十
个
2
8
4
8
6
8
0
1
3
1
5
十
个
1
十
个
0
3
1
3
5
3
十
个
0
5
1
5
3
5
因为十位上不能是0。
3×3=9
3×4=12
用2、1、0组成没有重复数字的两位数,分别是多少?
注意:0不能在十位上。
答:分别是21、20、12、10。
十
个
2
1
2
0
1
2
1
0
王强、小峰、小丽三个好朋友放学一起排队回家,他们有多少种不同的排法?
确定一名同学做第一名,把可能情况排完,然后再确定一名……
答:他们有6种不同的排法。
王强、小峰、小丽
王强、小丽、小峰
小峰、王强、小丽
小峰、小丽、王强
小丽、小峰、王强
小丽、王强、小峰
用0、2、4、6可以组成多少个没有重复数字的两位数?
确定除0以外的一个数字作十位,有3种排法,同样其它数字作十位也有3种排法。
答:可以组成9个没有重复数字的两位数。
3×3=9(个)
把5块巧克力全部分给小丽、小明、小红,每人至少分1块,有多少种分法?
列举找到所有可能性,做到不重复,不遗漏。
小丽
小明
小红
1
2
3
2
2
3
1
1
2
2
1
1
1
1
3
答:一共有6种分法。
方法一:
把5块巧克力全部分给小丽、小明、小红,每人至少分1块,有多少种分法?
1
1
2
2
小红
小明
小丽
小红
小明
小丽
小明
小丽
小红
小丽
答:一共有6种分法。
小明
小丽
小红
小丽
小明
小红
3
1
小明
小红
方法二:
0、1、2、3、4、5、6、7、8、9
0、1、2、3、4、5、6、7、8、9
10×10=100(种)
答:这个密码箱可以设置100种不同的密码。
两个数码孔可以分别为0~9中的一个数字,你知道这个密码箱可以设置多少种不同的密码吗?
把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
只有有害、厨余和可回收物垃圾桶才能摆在最左边
厨余、其它和可回收物垃圾桶三个摆一行有(
)种摆法。
①
②
③
④
有害
6
把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
有害、其它和可回收物垃圾桶三个摆一行有(
)种摆法。
①
②
③
④
厨余
6
把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
有害、其它和厨余垃圾桶三个摆一行有(
)种摆法。
①
②
③
④
可回收
6
把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
①
②
③
④
可回收物
有害、厨余和其它垃圾桶三个摆一行有(
)种摆法。
6
厨余
有害、其它和可回收物垃圾桶三个摆一行有(
)种摆法。
6
有害
厨余、其它和可回收物垃圾桶三个摆一行有(
)种摆法。
6
6+6+6=18(种)
答:一共有18种摆法。
组数问题
这节课你们都学会了哪些知识?
十个
3
0
31
35
50
51
53
1
0
13
15
用0、1、3、5能组成多少个没有重复数字的两位数?
解决数的排列问题,
可以用列举的方法,先考
虑高位,再考虑低位,有顺
序地依次排列,做到不重复不遗漏。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
搭
配
数学广角—搭配(二)
8
一、想一想,填一填。
1.用0、5、7三张卡片可以组成的两位数有(
)个,分别是(
)。
2.用3、0、5三张卡片可以组成的最大的三位数是(
),最小的三位数是(
),这两个数相差(
)。
举手回答!
4
50、57、70、75
530
305
225
二、排一排,有哪些不同的排法?再读一读。
不
怕
辣
不怕辣
可以组成的方案有:
不辣怕
怕辣不
怕不辣
辣不怕
辣怕不
一共有多少种穿法?
想一想:如何才能不重复、不遗漏的搭配呢?
每次上装和下装只能各穿1件。
一共有多少种穿法?
可以先确定一件上装,然后搭配不同的下装,再确定一件上装……
一共有6种穿法。
一共有多少种穿法?
我用
表示上装,
表示下装。
一共有6种穿法。
一共有多少种穿法?
一共有6种穿法。
我用A表示上装,B表示下装。
A1
A2
B1
B2
B3
搭配要有序,才能不重复,不遗漏。
A1
A2
B1
B2
B3
这两种方法都是先固定
,再选
。
上衣
裤子
先固定其中一种,再按顺序搭配。
搭配要有序,才能不重复、不遗漏。
对比观察,回答问题。
说一说:你发现了什么?
一件下装配2件上装,一共3个2种,2+2+2=6,有6种穿法。
想一想:先固定裤子,再固定上衣,有几种穿法?
答:可以有6种搭配方法。
乐乐餐饮店要推出新菜,荤菜有深海鱼头、豆瓣墨鱼仔,素菜有香菇素鸡、椒香莲藕、五彩蘑菇。每份饭有一荤一素两个菜,可以有多少种搭配方法?
用字母A代表荤菜。
用字母B代表荤菜。
A1
A2
B1
B2
B3
一组同学有10人,其中男生5人,女生5人,如果任意选中一位男生和一位女生,会有多少种不同的选法?
先确定一位男生,他可以和5个不同的女生组合,同样其它男生也可以和5个不同女生组合。
答:会有25种不同的选法。
5×5=25(种)
每个男生都有5种搭配方案,有5个男生。
拉动纸条,看看可以组成哪些两位数,记录下来。
当十位上是2时,组成的数有:
2
4
9
3
6
8
2
4
9
3
6
8
十位
个位
23、26、28
当十位上是4时,组成的数有:
43、46、48
当十位上是9时,组成的数有:
93、96、98
下面的早餐有多少种不同的搭配?
豆浆可以分别和下面4种点心搭配,牛奶也可以和下面4种点心搭配,则一共有4×2=8(种)。
豆浆
饮料和点心只能各选一种。
牛奶
蛋糕
油条
饼干
面包
如下图,小明从家到学校一共有多少种不同的路线?
先给不同的路进行编号。
答:小明从家到学校一共有4种不同的路线。
路线一:①③
小明家
图书馆
学校
①
②
③
④
路线二:①④
路线三:②③
路线四:②④
图中一共有多少个长方形?
①由一个长方形组成的:
4个
②由两个长方形组成的:
4个
③由四个长方形组成的:
1个
4+4+1=9(个)
答:一共有9个长方形。
搭配问题
这节课你们都学会了哪些知识?
A1
A2
B1
B2
B3
用图示法表示简单事物的组合,要按一定的顺序把要组合的事物两两相连,再数一数连了几条线,就可以得出结果。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
赛
场
数学广角—搭配(二)
8
国际足联世界杯简称“世界杯”,与奥运会并称为全球体育两大最顶级赛事。
这是什么?
大力神杯
2018年第21届世界杯在俄罗斯举行,第22届将在2022年卡塔尔举行。
世界杯开始前,每个地区会通过预选赛角逐出最终参赛的队伍,下面是亚洲杯的部分球队。
2011年亚洲杯足球赛A组球队如下。
每2个球队踢一场,一共要踢多少场?
卡塔尔
中国
韩国
乌兹别克斯坦
说一说你的思路。
2011年亚洲杯足球赛A组球队如下。
每个球队要和其他3个球队比赛,4×3=12(场)
卡塔尔
中国
韩国
乌兹别克斯坦
想一想:这样算对不对,说说你的想法。
一共要踢6场。
试着把任意两个球队连线。
①
④
⑤
⑥
③
②
想一想两队之间要连几条线?为什么?
两个球队之间连一条线就可以了,因为每两个队只比赛一次,不重复。
把4个球队摆成一排,再每个球队与其他3个球队分别连上线。
这条线要不要连呢?
第1队→第2队
第2队→第1队
每场比赛只与哪两个队有关,与两个队的顺序无关。
①
②
③
④
⑤
⑥
甲、乙、丙三支队伍参加排球赛,每两支队伍比赛一局,有几种不同的比赛方法?
答:有3种不同的比赛方法。
甲
乙
丙
每两个队进行连线,不要重复,不要遗漏。
答:有3种情况。
从3枚硬币中取出两个来,有多少种情况?
将3枚硬币编号。
①
②
③
任取两枚的情况有:①②、②③、①③。
7个小朋友在进行围棋比赛,每两个人都要赛一场,一共要进行多少场比赛?
将7个人用字母表示。
A
B
C
D
E
F
G
6+5+4+3+2+1=21(场)
答:一共要进行21场比赛。
6
5
4
3
2
1
有5个排球队进行比赛,每两队要踢一场比赛,一共要踢多少场?
答:一共要踢10场。
A
B
C
D
E
将5个排球队进行编号。
连线时要将其中一个球队与另外的每个球队连线,不要重复。
每次取2个,取出的钱共有哪几种情况?请写出来。
答:取出的钱有1元5分、1元5角、1元1角、5角5分、
1角5分,6角。
1元5分
1元5角
1元1角
5角5分
1角5分
6角
下面4个人每2个人通一次电话,一共要通多少次电话?
答:一共要通6次电话。
小刚、小红、小林、小丽
用字母代替4个人。
A
B
C
D
赛场问题
这节课你们都学会了哪些知识?
在解决排列、组合问题时,要按一定的顺序进行思考,在不重复、不遗漏的基础上把所有可能的情况找出来,可以借助直观连线法来解决。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
数学广角—搭配
8
练习二十二
用2、5、7、9组成没有重复数字的两位数,能组成多少个个位上是单数的两位数?
十
个
答:能组成9个个位上是单数的两位数。
可以先确定个位上的数字,然后依次跟剩余在十位上的数字组合。
5
单数有5、7、9。
2
7
5
9
5
个位上是5的两位数有3个,同样个位上是7、9的两位数也分别有3个。
先考虑低位,再考虑高位,有顺序地依次排列,一一列举出所有可能的数。
智慧老人告诉小黄开启智慧大门的密码是一个两位数。十位上是2、5、9中的一个,个位上是3、6、8中的一个,密码可能有几种情况?
可以用连线的方法解决。
答:密码可能有9种情况。
2
5
9
3
6
8
用图示法表示简单事物的组合,要按一定的顺序把要组合的事物两两相连,再数一数连了几条线,就可以得出结果。
甲、乙、丙、丁4个人参加乒乓球小组赛,每2人比赛一场,一共要比赛多少场?
答:一共要比赛6场。
甲
乙
丙
丁
先选定一个人,然后搭配其他人,接着再定一个人,去搭配还没有搭配过的人,以此类推。
用写有2、4、5、1的数字卡片,组成个位上是单数的两位数。能组成几种不同的两位数?
可以先确定个位上的数字,然后依次跟剩余在十位上的数字组合。
十
个
5
2
4
5
1
5
答:能组成6个个位是单数的两位数。
个位上是5的两位数有3个,同样个位是1的两位数也有3个。
唐僧师徒4人坐在椅子上。如果唐僧的位置不变,
其他人可以任意换位置,一共有多少种坐法?
一共有6种坐法
右图中一共有多少个长方形?
单个小长方形
2
2个小长方形组合
1
2+1=3
答:一共有3个长方形。
从鸟岛到狮虎山,共有多少条路线?
在统计路线时,只要路线之间不是完全重复,都可以算是一种新的路线。
①
②
③
④
⑤
⑥
路线一:①③⑤
路线二:①③⑥
路线五:②③⑤
路线六:②③⑥
路线三:①④⑤
路线四:①④⑥
路线七:②④⑤
路线八:②④⑥
答:共有8条路线。
用0、1、3、5可以组成多少个没有重复数字的两位数?
3×3=9(个)
答:可以组成9个没有重复数
字的两位数。
0不能作十位,先确定十位上的数字,再依次写出所有个位数字组合。
小丽、小红、小明、小强四位同学参加羽毛球赛,每2个人比赛一场,一共要比赛多少场?
用字母表示4个人。
答:一共要比赛6场。
A
B
C
D
从100到300的数中,有多少个十位和个位相同的数?
先确定百位数字,再看十位和百位相同的组合有多少种。
百位上是2时也是10个,再加上300这个数,共21个。
百
十
个
0
0
1
1
1
1
1
2
2
1
3
3
1
4
4
1
5
5
1
6
6
1
7
7
1
8
8
1
9
9
10
答:有21个十位和个位相同的数。
在解决排列、组合问题时,要按一定的顺序进行思考,在不重复、不遗漏的基础上把所有可能的情况找出来,可以借助直观连线法来解决。
这节课你们都学会了哪些知识?
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
数学广角——搭配(二)
我们的校园
8
校园里每天都会有许多问题要用数学来解决。
如果只有3000元的费用,请
你们提出换草皮的建议。
该换草皮了,这是草皮的价格表。
两块草坪同样大,长28米,宽16米。
有多少种不同的铺法?
分析:
如果东、西两块草坪铺不同的草,共有6种不同的铺法。
①
②
白三叶
高羊茅
天堂草
③
④
⑤
⑥
④⑤⑥与①②③的价钱相同。
分别算出每种方案的费用。
每块草坪的面积:28×16=448(平方米)
方案
白三叶费用(元)
高羊茅费用(元)
天堂草费用(元)
总费用(元)
1
2
3
2×448=896
3×448=1344
2240
2688
2×448=896
4×448=1792
3×448=1344
4×448=1792
3136
方案1和2都合理,方案3的费用超出了预算。
全部铺每平方米2元的白三叶最省钱。
还有其他方案吗,试着算一算!
全部使用高羊茅:
28×16×2×3=2688(元)
总费用:28×16×2×2=1792(元)
全部使用天堂草:
28×16×2×4=3584(元)
超过3000元
请你们帮体育老师设计一份赛程安排。要求如下:
比赛安排在15:00~16:30之间进行。
本周五下午课外活动时间,在东、西草坪举行三年级拔河比赛,请同学们去加油助威!
比赛地点是在东、西两块草坪。
三年级有4个班,先分组比赛,胜者再进行决赛。
每场比赛要用20分钟,准备10分钟。
可以用表格的形式通知比赛的时间和地点。
对阵
时间
地点
同学们还有其他的方法吗?
对阵
时间
地点
A组:三(1)—三(2)
15:10~15:30
东草坪
B组:三(3)
—三(4)
15:10~15:30
西草坪
A组胜者—B组胜者
15:40~16:00
东草坪
颁奖
16:10~16:20
西草坪
有多少不同的租法?
租车问题:学校计划在总费用3000元的限额内,利用汽车送234名学生和6名老师集体外出活动,现在有甲、乙、丙三种大客车,它们的载客量与租金如下表:
甲客车
乙客车
丙客车
载客量(人
/
辆)
50
40
30
租金(元
/
辆)
500
440
360
乘坐人数:234+6=240(人)
可以用列表法。
租车方案
租车费用
乘坐人数:234+6=240(人)
可以用列表法。
租车方案
租车费用
1
6辆乙客车
440×6=2640(元)
2
8辆丙客车
360×8=2880(元)
3
4辆甲客车+1辆乙客车
500×4+440×1=2440(元)
4
甲、乙、丙客车各2辆
(500+440+360)×2=2600(元)
……
……
同学们,可试着写出其它方案。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
部编人教版三年级数学下册
第8单元数学广角—搭配
【全单元】
PPT课件
组
数
数学广角—搭配(二)
8
他们都是谁?
孙悟空这个角色更深入人心,深受大家喜爱,当唐僧将他从五指山救出之后,给他取名叫“孙行者”。
《西游记》改编自明代小说家吴承恩同名文学古典名著,是中国文学史上一部最杰出的充满奇思异想的神魔小说。
下面三个字可以有多少种不同的组合?
孙
行
者
同桌交流:把所有可能都写下来,然后举手回答。
孙行者
行孙者
者行孙
孙者行
行者孙
者孙行
用0、1、3、5能组成多少个没有重复数字的两位数?
0
1
5
3
十位上不能是0。
小组交流:写下所有你能想到的数字。
十
个
把十位上是1的两位数写完,十位上再换一个数字。
1
0
1
3
1
5
这样可以不重复不遗漏。
用0、1、3、5能组成多少个没有重复数字的两位数?
我先选一个数字在十位上,可以按照从小到大的顺序。
照样子说出其他的数字,举手回答。
十
个
用同样的方法把5写在十位上。
3
0
3
1
3
5
5
0
5
1
5
3
选数字3在十位上,依次写出两位数。
用0、1、3、5能组成多少个没有重复数字的两位数?
3
0
3
1
3
5
5
0
5
1
5
3
1
0
1
3
1
5
答:能组成9个没有重复数字的两位数。
十位相同,个位不同的两位数各有3个。
用0、1、3、5能组成多少个没有重复数字的两位数?
用2、4、6、8能组成多少个没有重复数字的两位数?
注意:按照一定顺序排列。
4
2
6
2
8
十
个
2
十
个
2
4
6
4
8
4
十
个
2
6
4
6
8
6
十
个
2
8
4
8
6
8
十位相同,个位不同的两位数各有3个,所以一共能组成12个两位数。
想一想:都是用4个数字组成没有重复数字的两位数,为什么结果不同呢?
4
2
6
2
8
十
个
2
十
个
2
4
6
4
8
4
十
个
2
6
4
6
8
6
十
个
2
8
4
8
6
8
0
1
3
1
5
十
个
1
十
个
0
3
1
3
5
3
十
个
0
5
1
5
3
5
因为十位上不能是0。
3×3=9
3×4=12
用2、1、0组成没有重复数字的两位数,分别是多少?
注意:0不能在十位上。
答:分别是21、20、12、10。
十
个
2
1
2
0
1
2
1
0
王强、小峰、小丽三个好朋友放学一起排队回家,他们有多少种不同的排法?
确定一名同学做第一名,把可能情况排完,然后再确定一名……
答:他们有6种不同的排法。
王强、小峰、小丽
王强、小丽、小峰
小峰、王强、小丽
小峰、小丽、王强
小丽、小峰、王强
小丽、王强、小峰
用0、2、4、6可以组成多少个没有重复数字的两位数?
确定除0以外的一个数字作十位,有3种排法,同样其它数字作十位也有3种排法。
答:可以组成9个没有重复数字的两位数。
3×3=9(个)
把5块巧克力全部分给小丽、小明、小红,每人至少分1块,有多少种分法?
列举找到所有可能性,做到不重复,不遗漏。
小丽
小明
小红
1
2
3
2
2
3
1
1
2
2
1
1
1
1
3
答:一共有6种分法。
方法一:
把5块巧克力全部分给小丽、小明、小红,每人至少分1块,有多少种分法?
1
1
2
2
小红
小明
小丽
小红
小明
小丽
小明
小丽
小红
小丽
答:一共有6种分法。
小明
小丽
小红
小丽
小明
小红
3
1
小明
小红
方法二:
0、1、2、3、4、5、6、7、8、9
0、1、2、3、4、5、6、7、8、9
10×10=100(种)
答:这个密码箱可以设置100种不同的密码。
两个数码孔可以分别为0~9中的一个数字,你知道这个密码箱可以设置多少种不同的密码吗?
把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
只有有害、厨余和可回收物垃圾桶才能摆在最左边
厨余、其它和可回收物垃圾桶三个摆一行有(
)种摆法。
①
②
③
④
有害
6
把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
有害、其它和可回收物垃圾桶三个摆一行有(
)种摆法。
①
②
③
④
厨余
6
把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
有害、其它和厨余垃圾桶三个摆一行有(
)种摆法。
①
②
③
④
可回收
6
把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
①
②
③
④
可回收物
有害、厨余和其它垃圾桶三个摆一行有(
)种摆法。
6
厨余
有害、其它和可回收物垃圾桶三个摆一行有(
)种摆法。
6
有害
厨余、其它和可回收物垃圾桶三个摆一行有(
)种摆法。
6
6+6+6=18(种)
答:一共有18种摆法。
组数问题
这节课你们都学会了哪些知识?
十个
3
0
31
35
50
51
53
1
0
13
15
用0、1、3、5能组成多少个没有重复数字的两位数?
解决数的排列问题,
可以用列举的方法,先考
虑高位,再考虑低位,有顺
序地依次排列,做到不重复不遗漏。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
搭
配
数学广角—搭配(二)
8
一、想一想,填一填。
1.用0、5、7三张卡片可以组成的两位数有(
)个,分别是(
)。
2.用3、0、5三张卡片可以组成的最大的三位数是(
),最小的三位数是(
),这两个数相差(
)。
举手回答!
4
50、57、70、75
530
305
225
二、排一排,有哪些不同的排法?再读一读。
不
怕
辣
不怕辣
可以组成的方案有:
不辣怕
怕辣不
怕不辣
辣不怕
辣怕不
一共有多少种穿法?
想一想:如何才能不重复、不遗漏的搭配呢?
每次上装和下装只能各穿1件。
一共有多少种穿法?
可以先确定一件上装,然后搭配不同的下装,再确定一件上装……
一共有6种穿法。
一共有多少种穿法?
我用
表示上装,
表示下装。
一共有6种穿法。
一共有多少种穿法?
一共有6种穿法。
我用A表示上装,B表示下装。
A1
A2
B1
B2
B3
搭配要有序,才能不重复,不遗漏。
A1
A2
B1
B2
B3
这两种方法都是先固定
,再选
。
上衣
裤子
先固定其中一种,再按顺序搭配。
搭配要有序,才能不重复、不遗漏。
对比观察,回答问题。
说一说:你发现了什么?
一件下装配2件上装,一共3个2种,2+2+2=6,有6种穿法。
想一想:先固定裤子,再固定上衣,有几种穿法?
答:可以有6种搭配方法。
乐乐餐饮店要推出新菜,荤菜有深海鱼头、豆瓣墨鱼仔,素菜有香菇素鸡、椒香莲藕、五彩蘑菇。每份饭有一荤一素两个菜,可以有多少种搭配方法?
用字母A代表荤菜。
用字母B代表荤菜。
A1
A2
B1
B2
B3
一组同学有10人,其中男生5人,女生5人,如果任意选中一位男生和一位女生,会有多少种不同的选法?
先确定一位男生,他可以和5个不同的女生组合,同样其它男生也可以和5个不同女生组合。
答:会有25种不同的选法。
5×5=25(种)
每个男生都有5种搭配方案,有5个男生。
拉动纸条,看看可以组成哪些两位数,记录下来。
当十位上是2时,组成的数有:
2
4
9
3
6
8
2
4
9
3
6
8
十位
个位
23、26、28
当十位上是4时,组成的数有:
43、46、48
当十位上是9时,组成的数有:
93、96、98
下面的早餐有多少种不同的搭配?
豆浆可以分别和下面4种点心搭配,牛奶也可以和下面4种点心搭配,则一共有4×2=8(种)。
豆浆
饮料和点心只能各选一种。
牛奶
蛋糕
油条
饼干
面包
如下图,小明从家到学校一共有多少种不同的路线?
先给不同的路进行编号。
答:小明从家到学校一共有4种不同的路线。
路线一:①③
小明家
图书馆
学校
①
②
③
④
路线二:①④
路线三:②③
路线四:②④
图中一共有多少个长方形?
①由一个长方形组成的:
4个
②由两个长方形组成的:
4个
③由四个长方形组成的:
1个
4+4+1=9(个)
答:一共有9个长方形。
搭配问题
这节课你们都学会了哪些知识?
A1
A2
B1
B2
B3
用图示法表示简单事物的组合,要按一定的顺序把要组合的事物两两相连,再数一数连了几条线,就可以得出结果。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
赛
场
数学广角—搭配(二)
8
国际足联世界杯简称“世界杯”,与奥运会并称为全球体育两大最顶级赛事。
这是什么?
大力神杯
2018年第21届世界杯在俄罗斯举行,第22届将在2022年卡塔尔举行。
世界杯开始前,每个地区会通过预选赛角逐出最终参赛的队伍,下面是亚洲杯的部分球队。
2011年亚洲杯足球赛A组球队如下。
每2个球队踢一场,一共要踢多少场?
卡塔尔
中国
韩国
乌兹别克斯坦
说一说你的思路。
2011年亚洲杯足球赛A组球队如下。
每个球队要和其他3个球队比赛,4×3=12(场)
卡塔尔
中国
韩国
乌兹别克斯坦
想一想:这样算对不对,说说你的想法。
一共要踢6场。
试着把任意两个球队连线。
①
④
⑤
⑥
③
②
想一想两队之间要连几条线?为什么?
两个球队之间连一条线就可以了,因为每两个队只比赛一次,不重复。
把4个球队摆成一排,再每个球队与其他3个球队分别连上线。
这条线要不要连呢?
第1队→第2队
第2队→第1队
每场比赛只与哪两个队有关,与两个队的顺序无关。
①
②
③
④
⑤
⑥
甲、乙、丙三支队伍参加排球赛,每两支队伍比赛一局,有几种不同的比赛方法?
答:有3种不同的比赛方法。
甲
乙
丙
每两个队进行连线,不要重复,不要遗漏。
答:有3种情况。
从3枚硬币中取出两个来,有多少种情况?
将3枚硬币编号。
①
②
③
任取两枚的情况有:①②、②③、①③。
7个小朋友在进行围棋比赛,每两个人都要赛一场,一共要进行多少场比赛?
将7个人用字母表示。
A
B
C
D
E
F
G
6+5+4+3+2+1=21(场)
答:一共要进行21场比赛。
6
5
4
3
2
1
有5个排球队进行比赛,每两队要踢一场比赛,一共要踢多少场?
答:一共要踢10场。
A
B
C
D
E
将5个排球队进行编号。
连线时要将其中一个球队与另外的每个球队连线,不要重复。
每次取2个,取出的钱共有哪几种情况?请写出来。
答:取出的钱有1元5分、1元5角、1元1角、5角5分、
1角5分,6角。
1元5分
1元5角
1元1角
5角5分
1角5分
6角
下面4个人每2个人通一次电话,一共要通多少次电话?
答:一共要通6次电话。
小刚、小红、小林、小丽
用字母代替4个人。
A
B
C
D
赛场问题
这节课你们都学会了哪些知识?
在解决排列、组合问题时,要按一定的顺序进行思考,在不重复、不遗漏的基础上把所有可能的情况找出来,可以借助直观连线法来解决。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
数学广角—搭配
8
练习二十二
用2、5、7、9组成没有重复数字的两位数,能组成多少个个位上是单数的两位数?
十
个
答:能组成9个个位上是单数的两位数。
可以先确定个位上的数字,然后依次跟剩余在十位上的数字组合。
5
单数有5、7、9。
2
7
5
9
5
个位上是5的两位数有3个,同样个位上是7、9的两位数也分别有3个。
先考虑低位,再考虑高位,有顺序地依次排列,一一列举出所有可能的数。
智慧老人告诉小黄开启智慧大门的密码是一个两位数。十位上是2、5、9中的一个,个位上是3、6、8中的一个,密码可能有几种情况?
可以用连线的方法解决。
答:密码可能有9种情况。
2
5
9
3
6
8
用图示法表示简单事物的组合,要按一定的顺序把要组合的事物两两相连,再数一数连了几条线,就可以得出结果。
甲、乙、丙、丁4个人参加乒乓球小组赛,每2人比赛一场,一共要比赛多少场?
答:一共要比赛6场。
甲
乙
丙
丁
先选定一个人,然后搭配其他人,接着再定一个人,去搭配还没有搭配过的人,以此类推。
用写有2、4、5、1的数字卡片,组成个位上是单数的两位数。能组成几种不同的两位数?
可以先确定个位上的数字,然后依次跟剩余在十位上的数字组合。
十
个
5
2
4
5
1
5
答:能组成6个个位是单数的两位数。
个位上是5的两位数有3个,同样个位是1的两位数也有3个。
唐僧师徒4人坐在椅子上。如果唐僧的位置不变,
其他人可以任意换位置,一共有多少种坐法?
一共有6种坐法
右图中一共有多少个长方形?
单个小长方形
2
2个小长方形组合
1
2+1=3
答:一共有3个长方形。
从鸟岛到狮虎山,共有多少条路线?
在统计路线时,只要路线之间不是完全重复,都可以算是一种新的路线。
①
②
③
④
⑤
⑥
路线一:①③⑤
路线二:①③⑥
路线五:②③⑤
路线六:②③⑥
路线三:①④⑤
路线四:①④⑥
路线七:②④⑤
路线八:②④⑥
答:共有8条路线。
用0、1、3、5可以组成多少个没有重复数字的两位数?
3×3=9(个)
答:可以组成9个没有重复数
字的两位数。
0不能作十位,先确定十位上的数字,再依次写出所有个位数字组合。
小丽、小红、小明、小强四位同学参加羽毛球赛,每2个人比赛一场,一共要比赛多少场?
用字母表示4个人。
答:一共要比赛6场。
A
B
C
D
从100到300的数中,有多少个十位和个位相同的数?
先确定百位数字,再看十位和百位相同的组合有多少种。
百位上是2时也是10个,再加上300这个数,共21个。
百
十
个
0
0
1
1
1
1
1
2
2
1
3
3
1
4
4
1
5
5
1
6
6
1
7
7
1
8
8
1
9
9
10
答:有21个十位和个位相同的数。
在解决排列、组合问题时,要按一定的顺序进行思考,在不重复、不遗漏的基础上把所有可能的情况找出来,可以借助直观连线法来解决。
这节课你们都学会了哪些知识?
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
数学广角——搭配(二)
我们的校园
8
校园里每天都会有许多问题要用数学来解决。
如果只有3000元的费用,请
你们提出换草皮的建议。
该换草皮了,这是草皮的价格表。
两块草坪同样大,长28米,宽16米。
有多少种不同的铺法?
分析:
如果东、西两块草坪铺不同的草,共有6种不同的铺法。
①
②
白三叶
高羊茅
天堂草
③
④
⑤
⑥
④⑤⑥与①②③的价钱相同。
分别算出每种方案的费用。
每块草坪的面积:28×16=448(平方米)
方案
白三叶费用(元)
高羊茅费用(元)
天堂草费用(元)
总费用(元)
1
2
3
2×448=896
3×448=1344
2240
2688
2×448=896
4×448=1792
3×448=1344
4×448=1792
3136
方案1和2都合理,方案3的费用超出了预算。
全部铺每平方米2元的白三叶最省钱。
还有其他方案吗,试着算一算!
全部使用高羊茅:
28×16×2×3=2688(元)
总费用:28×16×2×2=1792(元)
全部使用天堂草:
28×16×2×4=3584(元)
超过3000元
请你们帮体育老师设计一份赛程安排。要求如下:
比赛安排在15:00~16:30之间进行。
本周五下午课外活动时间,在东、西草坪举行三年级拔河比赛,请同学们去加油助威!
比赛地点是在东、西两块草坪。
三年级有4个班,先分组比赛,胜者再进行决赛。
每场比赛要用20分钟,准备10分钟。
可以用表格的形式通知比赛的时间和地点。
对阵
时间
地点
同学们还有其他的方法吗?
对阵
时间
地点
A组:三(1)—三(2)
15:10~15:30
东草坪
B组:三(3)
—三(4)
15:10~15:30
西草坪
A组胜者—B组胜者
15:40~16:00
东草坪
颁奖
16:10~16:20
西草坪
有多少不同的租法?
租车问题:学校计划在总费用3000元的限额内,利用汽车送234名学生和6名老师集体外出活动,现在有甲、乙、丙三种大客车,它们的载客量与租金如下表:
甲客车
乙客车
丙客车
载客量(人
/
辆)
50
40
30
租金(元
/
辆)
500
440
360
乘坐人数:234+6=240(人)
可以用列表法。
租车方案
租车费用
乘坐人数:234+6=240(人)
可以用列表法。
租车方案
租车费用
1
6辆乙客车
440×6=2640(元)
2
8辆丙客车
360×8=2880(元)
3
4辆甲客车+1辆乙客车
500×4+440×1=2440(元)
4
甲、乙、丙客车各2辆
(500+440+360)×2=2600(元)
……
……
同学们,可试着写出其它方案。
课堂感想
1、这节课你有什么收获?
2、这节课还有什么疑惑?
说出来和大家一起交流吧!
谢谢观赏!
再见!
