一年级上册数学教案-3. 8 20以内数及其加减法(数墙) 沪教版
文档属性
| 名称 | 一年级上册数学教案-3. 8 20以内数及其加减法(数墙) 沪教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 211.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 13:32:42 | ||
图片预览

文档简介
课题:数墙
教学目标: 1. 能正确、熟练地计算20以内的加减法。
2. 在观察、比较、分析的过程中,探索数与数之间的关系,有效利用规则进行填数。
3. 尝试用数与数之间的关系解决问题,培养初步的策略意识。
二、目标制定的依据:
1. 教材分析:
《数字的墙》这一内容,是一年级上册第三单元《20以内的数及其加减法》的最后一个内容。它通过一种新的练习形式,以较少的笔墨蕴藏了大量的加减法题,是对前期所学的20以内加减法计算的复习与巩固。同时,要填出“数字的墙”中空缺的一些数,必然要找到隐藏在其中的规律,过程中对规律的寻找与探究能力也为后续的学习打下基础。在这节课中,对于“数墙”的认识与运用,需要经历“寻找规律——运用规律填数”的过程,而对于“每块数砖是它底下两块数砖的和”的规律运用,更需要在过程中提炼“知二求三”的策略。因此,本节课的学习,除了关注计算熟练度与正确率的提高外,更大的价值在于引导学生进行规律的探究、“知二求三”解题策略的意识渗透,期望学生能获得这种意识,并能自觉运用于后续的问题解决中。
2. 学情分析:
之前,学生已经掌握了加减法的意义,也能比较熟练地进行20以内加减法的计算,这些都为本节课的学习奠定了基础,因此对于数墙中的加减运算学生不会困难。对于规律的探究,前期学习中也适当接触过一些,相应的能力也是具备的,但是对于规律的描述,学生大多能意会,或者停留在“3+5=8”的算式描述阶段,还无法上升到“每块数砖是它底下两块数砖的和”的规范语言来表达。如果过程中过分强调学生用这样的语言,那可能会形成机械的训练,是不利于学生思维发展的。因此,为了帮助学生理解与表达,我们将每次有直接关联的3个格子用“品字格”进行形象地概括,并引导学生联系前期学习的“部总关系”来表达三个数之间的关系,这样简洁又易懂。而在填数策略的提炼中,我们也适时地引导学生进行思辨,利用前面梳理的“部总关系”,得到“知二求三”的策略。
教学过程
教学环节 教师活动 学生活动 设计意图
常规积累 找规律填数
16、14、12、10、( )、( ) 独立思考 复习前期规律研究,为后续自主探究铺垫。
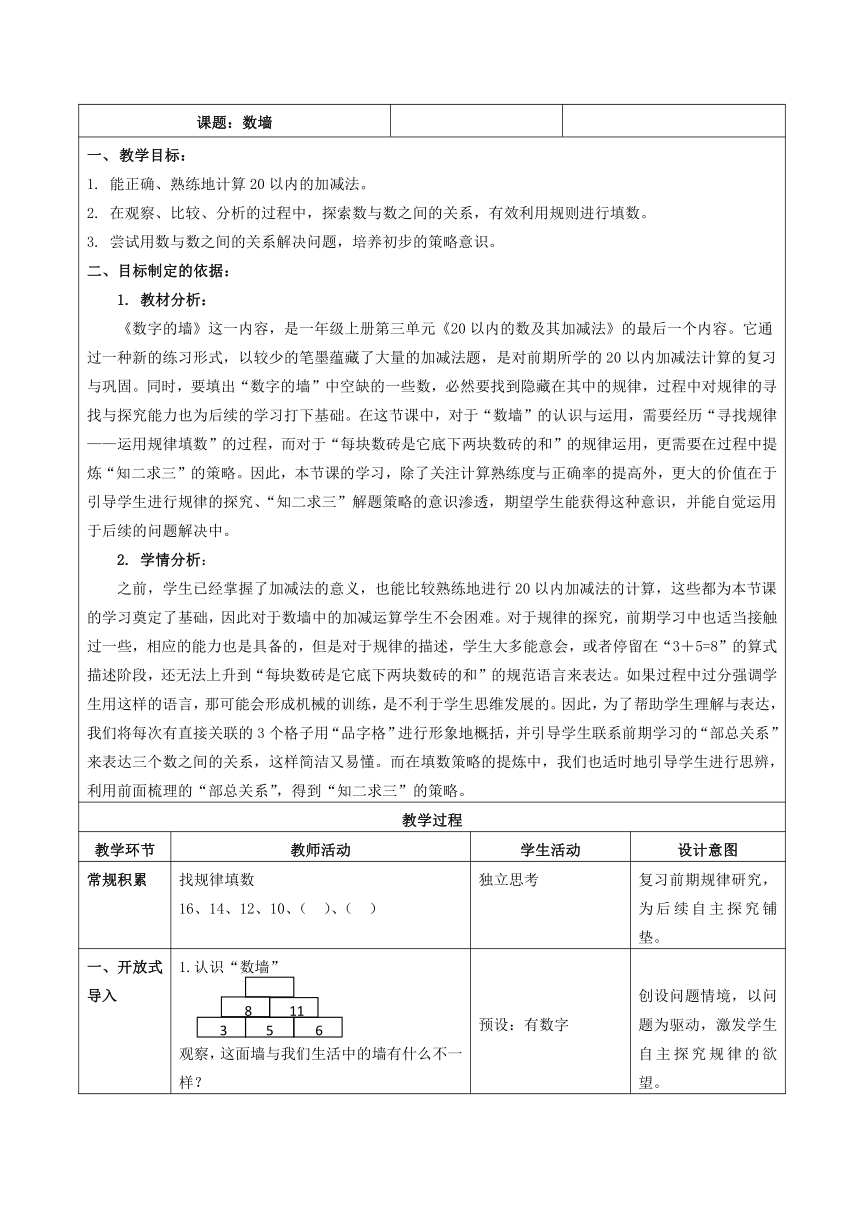
一、开放式导入 1.认识“数墙”
观察,这面墙与我们生活中的墙有什么不一样?
板书课题:数墙
预设:有数字
创设问题情境,以问题为驱动,激发学生自主探究规律的欲望。
二、核心过程推进(探究数墙的规律)
1. 观察发现数墙的规律
仔细观察是怎样往上造第二层的?你知道最上面一块是几吗?你是怎么想的?
2. 提炼小结三块砖之间的联系
(1)整体梳理造墙的过程
完整说说这三块砖是怎样一步步造的?
每一次造的时候,哪几块砖之间是有联系的?有什么联系?
(2)借助“品”字格提炼规律
3. 小结
在品字格中,下面两个数的和等于上面这个数 预设:
S1:8+9=11
S2:3+5=8,5+6=11,8+11=19
预设:
S1:3+5=8,5+6=11,8+11=19
S2:3,5,8之间是有联系的;5,6,11之间是有联系的;8,11,19之间是有联系的;
S3:下面相邻两个数的和是这两个数上面的数。
观察数墙,探究规律
寻找有联系的三块砖,为后续的填数做准备。
借助“品字格”简洁表达三个数之间的关系
三、规律的巩固与运用(运用数墙规律来填数) 1. 巩固数墙规律
仔细观察,你准备先造哪一块?为什么?
过程中辨析:
可不可以先算蓝色这块呢?为什么?
2. 提炼“知二求三”的策略
准备先造那一块砖?
小结:原来品字格中,必须知道2个数,才能求出第3个数。
3. 运用策略,思考解题路径
独立填写
填写后,说说是怎样填写的。
S:不能。蓝色这块砖所在的品字格里,只知道1个数,另外2个数都没有办法确定。
跟进练习,及时巩固数墙规律
“知二求三”的初步感知
运用规则、计算数墙,在分析思辨中培养整体把握意识和策略意识。
四、拓展延伸 在造数墙的时候,我们发现已知2个数来求地3个数,你能不能把这种方法运用到其他地方去呢?
1. 要使横行、竖行相加的和都等于10,框里填几呢?
小结:在这个问题里也是3个数里知道2个数,才能求出第3个数,这是重要的解决问题的方法。
2. 在 ○ 里填数,使每条线上三个数相加的和都等于12。
3. 在 ○ 里填数,使每条线上三个数相加的和都等于14。
填写后,说说是怎样填写的。
能把 “已知2个数来求第3个数”的规律迁移到其他问题解决中。
依时间而定,可适当作为课后拓展
五、总结 通过今天的学习,你学到了哪些本领?
教学目标: 1. 能正确、熟练地计算20以内的加减法。
2. 在观察、比较、分析的过程中,探索数与数之间的关系,有效利用规则进行填数。
3. 尝试用数与数之间的关系解决问题,培养初步的策略意识。
二、目标制定的依据:
1. 教材分析:
《数字的墙》这一内容,是一年级上册第三单元《20以内的数及其加减法》的最后一个内容。它通过一种新的练习形式,以较少的笔墨蕴藏了大量的加减法题,是对前期所学的20以内加减法计算的复习与巩固。同时,要填出“数字的墙”中空缺的一些数,必然要找到隐藏在其中的规律,过程中对规律的寻找与探究能力也为后续的学习打下基础。在这节课中,对于“数墙”的认识与运用,需要经历“寻找规律——运用规律填数”的过程,而对于“每块数砖是它底下两块数砖的和”的规律运用,更需要在过程中提炼“知二求三”的策略。因此,本节课的学习,除了关注计算熟练度与正确率的提高外,更大的价值在于引导学生进行规律的探究、“知二求三”解题策略的意识渗透,期望学生能获得这种意识,并能自觉运用于后续的问题解决中。
2. 学情分析:
之前,学生已经掌握了加减法的意义,也能比较熟练地进行20以内加减法的计算,这些都为本节课的学习奠定了基础,因此对于数墙中的加减运算学生不会困难。对于规律的探究,前期学习中也适当接触过一些,相应的能力也是具备的,但是对于规律的描述,学生大多能意会,或者停留在“3+5=8”的算式描述阶段,还无法上升到“每块数砖是它底下两块数砖的和”的规范语言来表达。如果过程中过分强调学生用这样的语言,那可能会形成机械的训练,是不利于学生思维发展的。因此,为了帮助学生理解与表达,我们将每次有直接关联的3个格子用“品字格”进行形象地概括,并引导学生联系前期学习的“部总关系”来表达三个数之间的关系,这样简洁又易懂。而在填数策略的提炼中,我们也适时地引导学生进行思辨,利用前面梳理的“部总关系”,得到“知二求三”的策略。
教学过程
教学环节 教师活动 学生活动 设计意图
常规积累 找规律填数
16、14、12、10、( )、( ) 独立思考 复习前期规律研究,为后续自主探究铺垫。
一、开放式导入 1.认识“数墙”
观察,这面墙与我们生活中的墙有什么不一样?
板书课题:数墙
预设:有数字
创设问题情境,以问题为驱动,激发学生自主探究规律的欲望。
二、核心过程推进(探究数墙的规律)
1. 观察发现数墙的规律
仔细观察是怎样往上造第二层的?你知道最上面一块是几吗?你是怎么想的?
2. 提炼小结三块砖之间的联系
(1)整体梳理造墙的过程
完整说说这三块砖是怎样一步步造的?
每一次造的时候,哪几块砖之间是有联系的?有什么联系?
(2)借助“品”字格提炼规律
3. 小结
在品字格中,下面两个数的和等于上面这个数 预设:
S1:8+9=11
S2:3+5=8,5+6=11,8+11=19
预设:
S1:3+5=8,5+6=11,8+11=19
S2:3,5,8之间是有联系的;5,6,11之间是有联系的;8,11,19之间是有联系的;
S3:下面相邻两个数的和是这两个数上面的数。
观察数墙,探究规律
寻找有联系的三块砖,为后续的填数做准备。
借助“品字格”简洁表达三个数之间的关系
三、规律的巩固与运用(运用数墙规律来填数) 1. 巩固数墙规律
仔细观察,你准备先造哪一块?为什么?
过程中辨析:
可不可以先算蓝色这块呢?为什么?
2. 提炼“知二求三”的策略
准备先造那一块砖?
小结:原来品字格中,必须知道2个数,才能求出第3个数。
3. 运用策略,思考解题路径
独立填写
填写后,说说是怎样填写的。
S:不能。蓝色这块砖所在的品字格里,只知道1个数,另外2个数都没有办法确定。
跟进练习,及时巩固数墙规律
“知二求三”的初步感知
运用规则、计算数墙,在分析思辨中培养整体把握意识和策略意识。
四、拓展延伸 在造数墙的时候,我们发现已知2个数来求地3个数,你能不能把这种方法运用到其他地方去呢?
1. 要使横行、竖行相加的和都等于10,框里填几呢?
小结:在这个问题里也是3个数里知道2个数,才能求出第3个数,这是重要的解决问题的方法。
2. 在 ○ 里填数,使每条线上三个数相加的和都等于12。
3. 在 ○ 里填数,使每条线上三个数相加的和都等于14。
填写后,说说是怎样填写的。
能把 “已知2个数来求第3个数”的规律迁移到其他问题解决中。
依时间而定,可适当作为课后拓展
五、总结 通过今天的学习,你学到了哪些本领?
