18.1 勾股定理(15张)
文档属性
| 名称 | 18.1 勾股定理(15张) |
|
|
| 格式 | zip | ||
| 文件大小 | 652.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-11 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
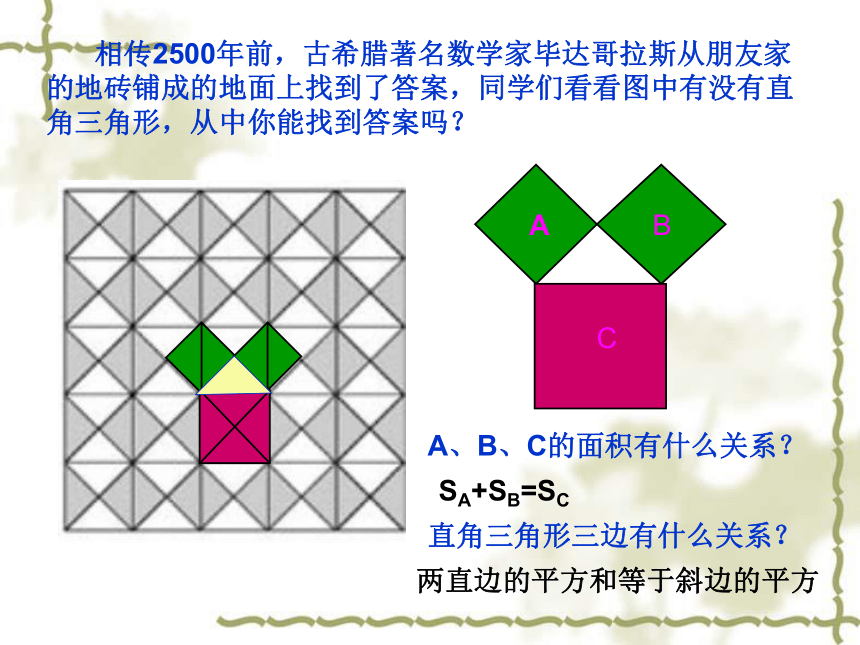
18.1 勾股定理
a
b
c
勾股定理——千古第一定理
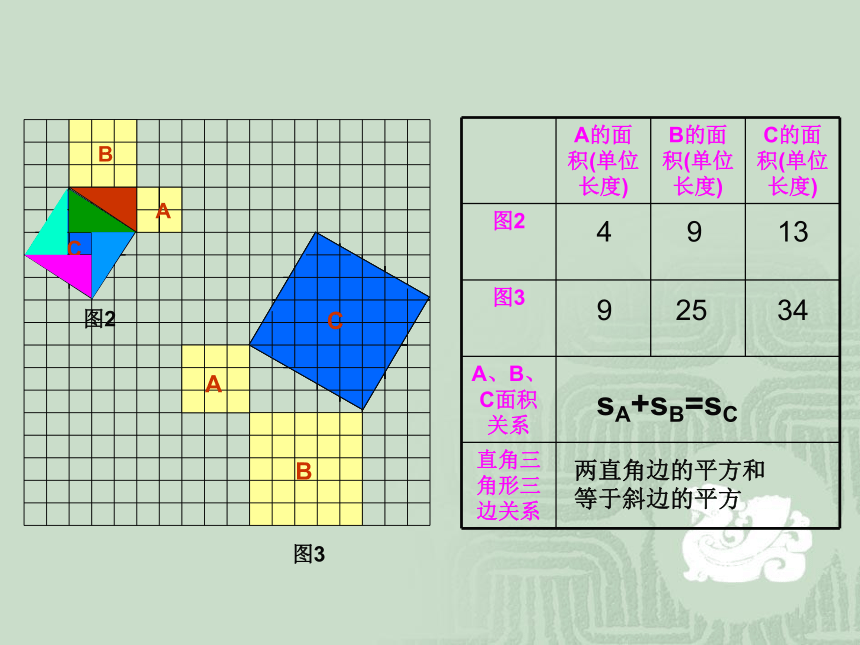
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?
A
B
C
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
A
B
C
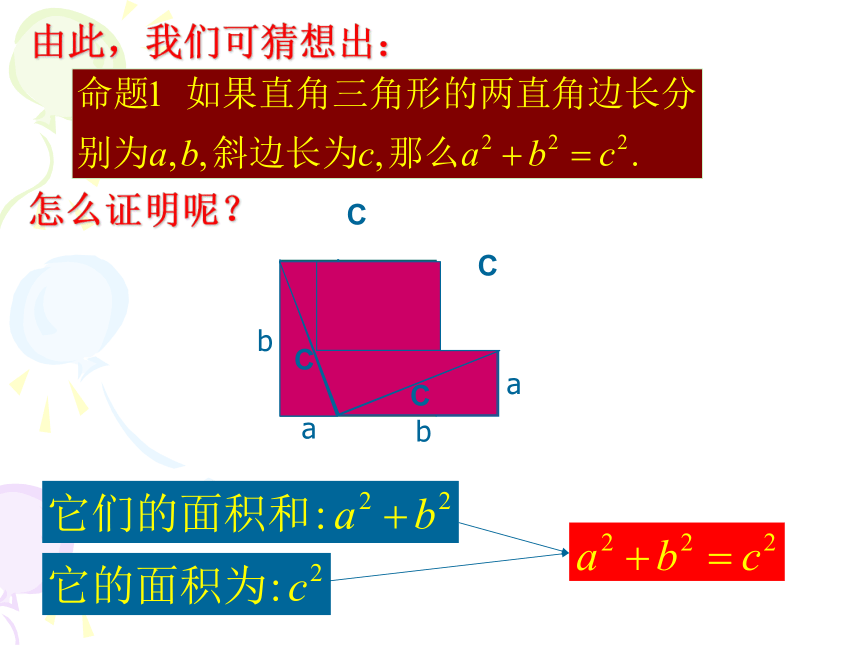
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
由此,我们可猜想出:
b
a
a
怎么证明呢?
C
C
C
C
b
由此,我们可猜想出:
a
b
c
b
c
a
大正方形面积:
还可看作四个直角三角形和一个小正方形之和:
即:
经过证明被确认正确的命题叫做定理.
a
b
c
1、证明:
s大正方形=(a+b)2=a2+2ab+b2
s大正方形=c2+4× ab=c2+2ab
∵s大正方形=s大正方形
∴a2+2ab+b2=c2+2ab
∴a2+b2=c2
还有其他证明方法吗?
伽菲尔德证法:
a
a
b
b
c
c
s梯形= (a+b)(a+b)= (a2+2ab+b2)
= a2+ab+ b2
s梯形=2× ab+ c2=ab+ c2
∵s梯形=s梯形 ∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
c
a
b
勾
股
弦
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
试一试:
3
4
2、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )
A
B
C
A.5米 B.12米 C.10米 D.13米
13
12
A
试一试:
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A 2、4、6
C 4、6、8
B
试一试:
B 6、8、10
D 8、10、12
5 或
4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
例2.已知:如图,等边△ABC的边长是 6 .
(1)求高AD的长;
(2)求S△ABC .
A
B
C
D
例题分析
3
6
已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .
A
B
C
D
练一练
18.1 勾股定理
a
b
c
勾股定理——千古第一定理
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?
A
B
C
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
A
B
C
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
由此,我们可猜想出:
b
a
a
怎么证明呢?
C
C
C
C
b
由此,我们可猜想出:
a
b
c
b
c
a
大正方形面积:
还可看作四个直角三角形和一个小正方形之和:
即:
经过证明被确认正确的命题叫做定理.
a
b
c
1、证明:
s大正方形=(a+b)2=a2+2ab+b2
s大正方形=c2+4× ab=c2+2ab
∵s大正方形=s大正方形
∴a2+2ab+b2=c2+2ab
∴a2+b2=c2
还有其他证明方法吗?
伽菲尔德证法:
a
a
b
b
c
c
s梯形= (a+b)(a+b)= (a2+2ab+b2)
= a2+ab+ b2
s梯形=2× ab+ c2=ab+ c2
∵s梯形=s梯形 ∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
c
a
b
勾
股
弦
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
试一试:
3
4
2、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )
A
B
C
A.5米 B.12米 C.10米 D.13米
13
12
A
试一试:
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A 2、4、6
C 4、6、8
B
试一试:
B 6、8、10
D 8、10、12
5 或
4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
例2.已知:如图,等边△ABC的边长是 6 .
(1)求高AD的长;
(2)求S△ABC .
A
B
C
D
例题分析
3
6
已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .
A
B
C
D
练一练
