勾股定理证明(20张)
图片预览




文档简介
(共21张PPT)
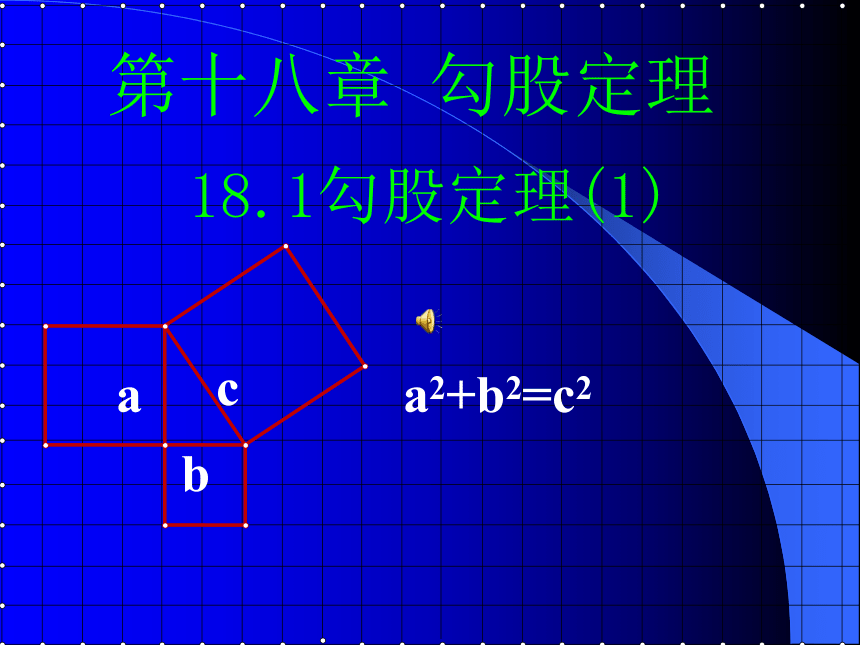
第十八章 勾股定理
b
a
c
a2+b2=c2
18.1勾股定理(1)
读一读
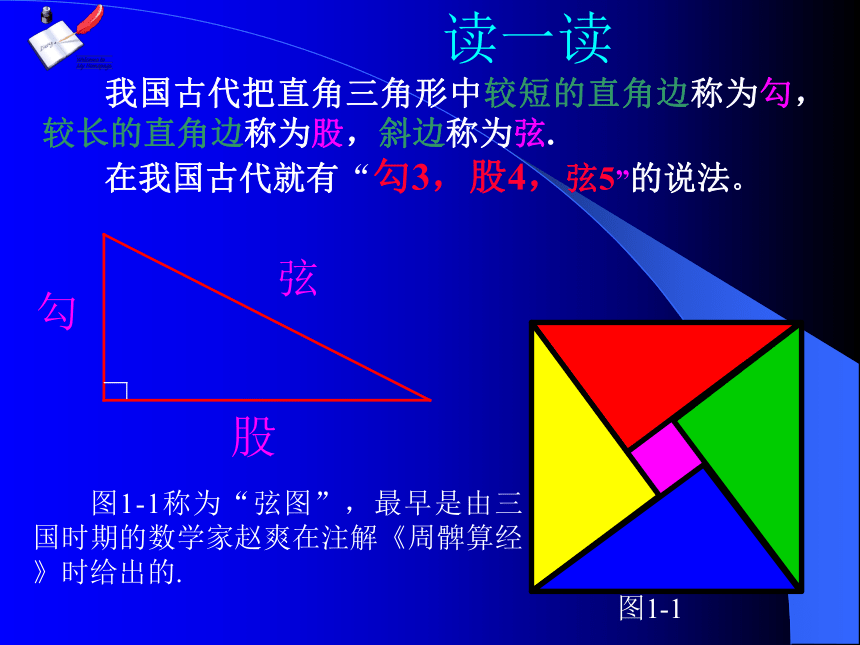
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.
在我国古代就有“勾3,股4,弦5”的说法。
图1-1
股
勾
弦
图1-1称为“弦图”,最早是由三国时期的数学家赵爽在注解《周髀算经》时给出的.
左下图是2002年在北京召开的国际数学家大会会徽, 其图案正是“弦图”,它标志着中国古代的数学成就.
学习目标
※探索直角三角形三边关系,掌握勾股定理的运用思想,发展数学思维。
※经历观察与发现直角三角形三边关系的 过程,感受勾股定理的应用意识。
※培养严谨的数学学习的态度,体会勾股定理的应用价值。
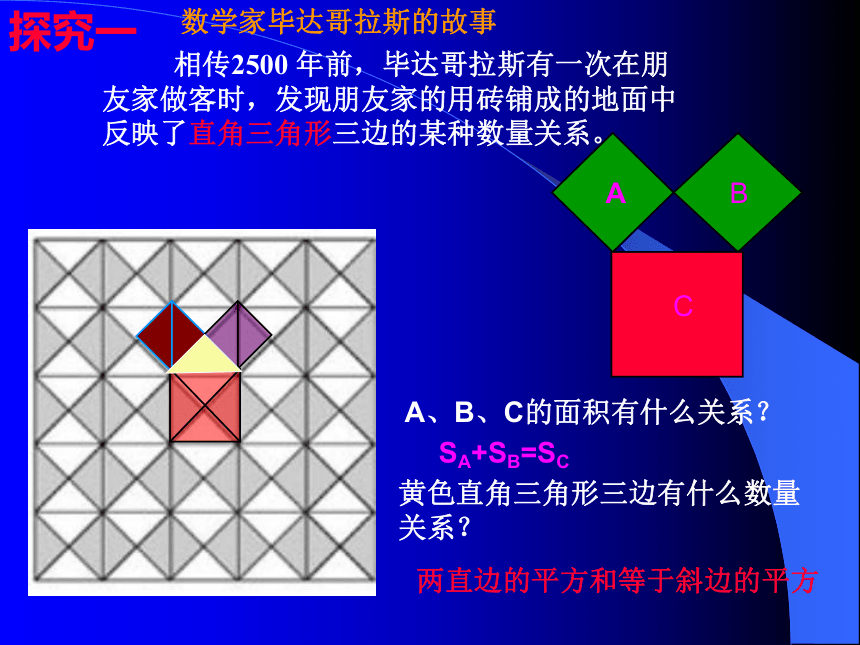
数学家毕达哥拉斯的故事
A、B、C的面积有什么关系?
黄色直角三角形三边有什么数量
关系?
SA+SB=SC
两直边的平方和等于斜边的平方
探究一
A
B
C
相传2500 年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。
A
B
C
图1—1
(1)观察图1—1:
正方形A中含有 个小方格,即A的面积是 个单位面积;
正方形B中含有 个小方格,即B的面积是 个单位面积;
正方形C中含有 个小方格,即C的面积是 个单位面积;
9
9
9
9
18
18
A的面积+ B的面积= C的面积
对于等腰直角三角形有这样的性质:
对于任意直角三角形都有这样的性质吗?
两直边的平方和等于斜边的平方
看下图
A
B
C
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
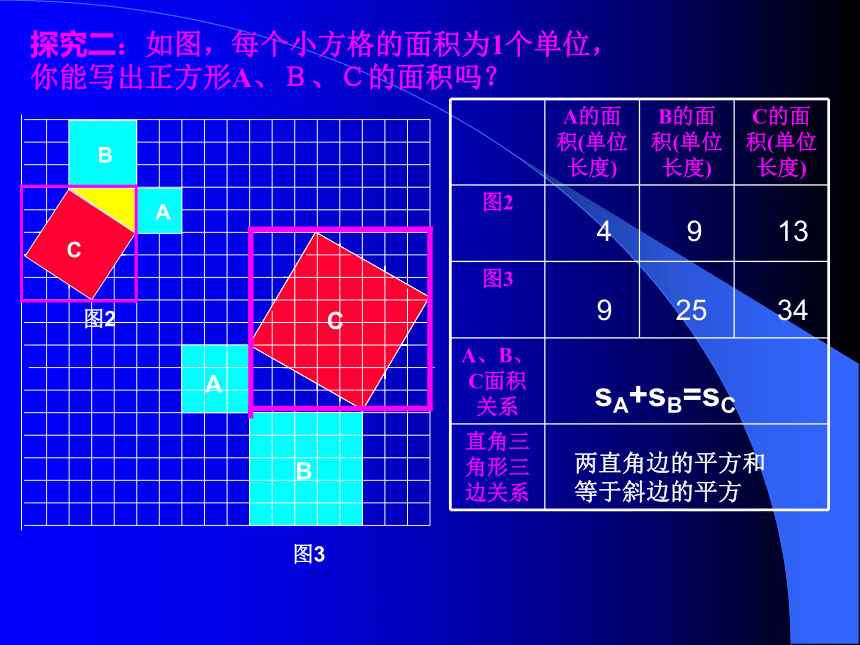
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
A
B
C
探究二:如图,每个小方格的面积为1个单位, 你能写出正方形A、B、C的面积吗?
a
b
c
c2=a2 + b2
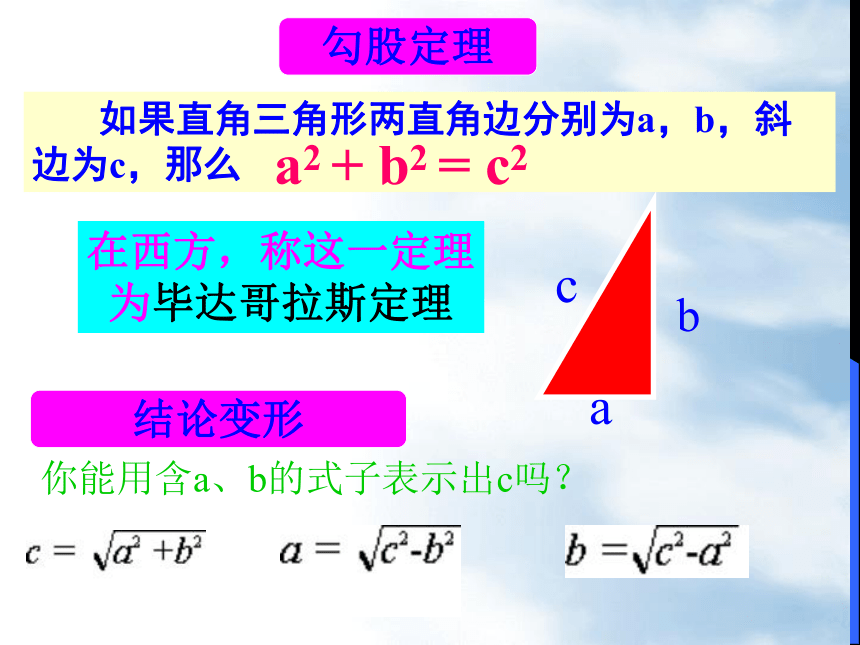
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
结论变形
你能用含a、b的式子表示出c吗?
在西方,称这一定理为毕达哥拉斯定理
c
b a
∵ c2 = (b a)2 + 4( ab)
= a2 2ab + b2 + 2ab
c2 = a2 + b2
勾股定理的证实(一)
3世纪我国汉代的赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形。
(思考)大正方形的面积、 4个三角形的面积、小正方形的面积有何关系?你能据此证实勾股定理吗?
赵爽弦图
a
b
“赵爽弦图”表现了我国古代人对数学的钻研精神和聪明才智,它是我国数学的骄傲。
正因为此,这个图案被选为2002年在北京召开的国际数学家大会会徽。
勾股定理的证实(二)
在1876年一个周末的傍晚,美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国共和党议员伽菲尔德.
他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么。
伽菲尔德循声向两个小孩走去, 只见一个小男孩正俯着身子,用树枝在地上画一个直角三角形,于是伽菲尔德便问,你们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别是3和4,那么斜边长为多少呢?”
伽菲尔德答到:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少呢?”伽菲尔德不假思索地回答到:“那斜边的平方,一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?……”
伽菲尔德一时语塞,无法解释了,心理很不是滋味。于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题。伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.
(a + b)(b + a) = c2 + 2( ab)
a2 + ab + b2 = c2 + ab
a2 + b2 = c2
a
a
b
b
c
c
1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
∟
∟
∟
c
c
目前,世界上共有500多种证明“勾股定理”的方法。
8
15
A
49
B
25
1.求下列图中字母所代表的正方形的面积:
y=0
学以致用,做一做
y=0
2.求出下列直角三角形中未知边的长度
6
8
x
3
x
5
学以致用,做一做
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
X2 =36+64
x2 =100
x2=62+82
∴ x=10
∵x>0
x2+32=52
x2=52-32
x2=16
∴ x=4
(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2
∵x>0
A
C
B
A
C
B
如图,在△ABC中, ∠C=90°,a=5,b=12,
则c=____
13
y=0
展示交流
C
B
A
c
a
b
在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________
10 或
y=0
补偿提高
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b平方和, 等于斜边c平方。
a2+b2 =c2
⒊勾股定理的主要作用是在直角三角形中,已知任意两边求第三边的长。
P69--70 1、2、3
第十八章 勾股定理
b
a
c
a2+b2=c2
18.1勾股定理(1)
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.
在我国古代就有“勾3,股4,弦5”的说法。
图1-1
股
勾
弦
图1-1称为“弦图”,最早是由三国时期的数学家赵爽在注解《周髀算经》时给出的.
左下图是2002年在北京召开的国际数学家大会会徽, 其图案正是“弦图”,它标志着中国古代的数学成就.
学习目标
※探索直角三角形三边关系,掌握勾股定理的运用思想,发展数学思维。
※经历观察与发现直角三角形三边关系的 过程,感受勾股定理的应用意识。
※培养严谨的数学学习的态度,体会勾股定理的应用价值。
数学家毕达哥拉斯的故事
A、B、C的面积有什么关系?
黄色直角三角形三边有什么数量
关系?
SA+SB=SC
两直边的平方和等于斜边的平方
探究一
A
B
C
相传2500 年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。
A
B
C
图1—1
(1)观察图1—1:
正方形A中含有 个小方格,即A的面积是 个单位面积;
正方形B中含有 个小方格,即B的面积是 个单位面积;
正方形C中含有 个小方格,即C的面积是 个单位面积;
9
9
9
9
18
18
A的面积+ B的面积= C的面积
对于等腰直角三角形有这样的性质:
对于任意直角三角形都有这样的性质吗?
两直边的平方和等于斜边的平方
看下图
A
B
C
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
A
B
C
探究二:如图,每个小方格的面积为1个单位, 你能写出正方形A、B、C的面积吗?
a
b
c
c2=a2 + b2
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
结论变形
你能用含a、b的式子表示出c吗?
在西方,称这一定理为毕达哥拉斯定理
c
b a
∵ c2 = (b a)2 + 4( ab)
= a2 2ab + b2 + 2ab
c2 = a2 + b2
勾股定理的证实(一)
3世纪我国汉代的赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形。
(思考)大正方形的面积、 4个三角形的面积、小正方形的面积有何关系?你能据此证实勾股定理吗?
赵爽弦图
a
b
“赵爽弦图”表现了我国古代人对数学的钻研精神和聪明才智,它是我国数学的骄傲。
正因为此,这个图案被选为2002年在北京召开的国际数学家大会会徽。
勾股定理的证实(二)
在1876年一个周末的傍晚,美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国共和党议员伽菲尔德.
他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么。
伽菲尔德循声向两个小孩走去, 只见一个小男孩正俯着身子,用树枝在地上画一个直角三角形,于是伽菲尔德便问,你们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别是3和4,那么斜边长为多少呢?”
伽菲尔德答到:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少呢?”伽菲尔德不假思索地回答到:“那斜边的平方,一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?……”
伽菲尔德一时语塞,无法解释了,心理很不是滋味。于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题。伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.
(a + b)(b + a) = c2 + 2( ab)
a2 + ab + b2 = c2 + ab
a2 + b2 = c2
a
a
b
b
c
c
1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
∟
∟
∟
c
c
目前,世界上共有500多种证明“勾股定理”的方法。
8
15
A
49
B
25
1.求下列图中字母所代表的正方形的面积:
y=0
学以致用,做一做
y=0
2.求出下列直角三角形中未知边的长度
6
8
x
3
x
5
学以致用,做一做
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
X2 =36+64
x2 =100
x2=62+82
∴ x=10
∵x>0
x2+32=52
x2=52-32
x2=16
∴ x=4
(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2
∵x>0
A
C
B
A
C
B
如图,在△ABC中, ∠C=90°,a=5,b=12,
则c=____
13
y=0
展示交流
C
B
A
c
a
b
在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________
10 或
y=0
补偿提高
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b平方和, 等于斜边c平方。
a2+b2 =c2
⒊勾股定理的主要作用是在直角三角形中,已知任意两边求第三边的长。
P69--70 1、2、3
