勾股定理(复习课)(14张)
文档属性
| 名称 | 勾股定理(复习课)(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 526.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-11 15:31:17 | ||
图片预览



文档简介
(共15张PPT)
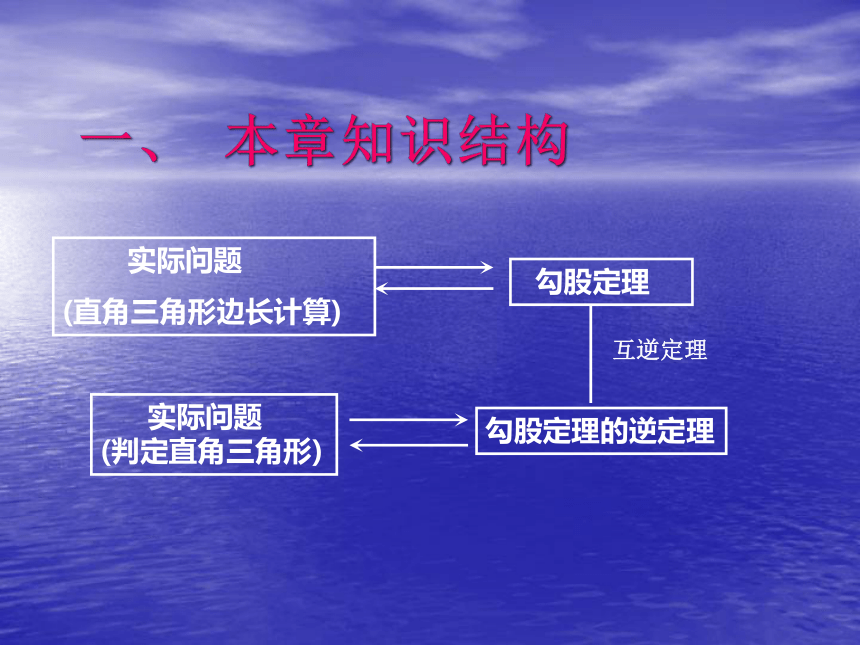
实际问题
(直角三角形边长计算)
勾股定理
勾股定理的逆定理
实际问题
(判定直角三角形)
互逆定理
1.直角三角形三边的长有什么关系 找一个实际问题并用勾股定理解决.
2.已知一个三角形的三边,你能判断它是否直角三角形吗
3.如果一个命题成立,它的逆命题一定成立吗 请举例说明.
(1)求出图形中的x
(3)在下列几组数中,能组成直角三角形的有几组?
6,8,10;5,12,13;8,40,41;
3(a-1),4(a-1),5(a-1)(a>1)
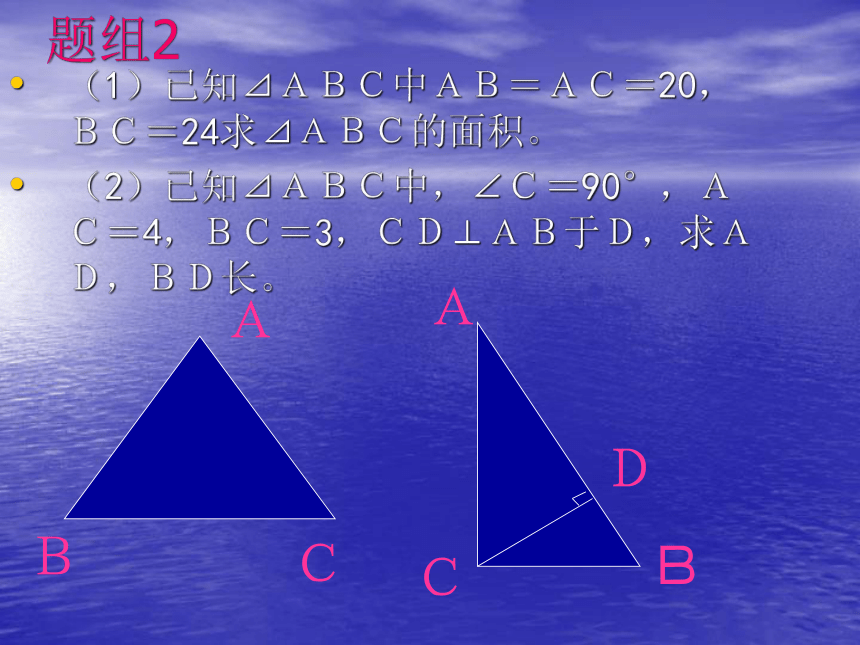
(1)已知⊿ABC中AB=AC=20,BC=24求⊿ABC的面积。
(2)已知⊿ABC中,∠C=90°,AC=4,BC=3,CD⊥AB于D,求AD,BD长。
A
B
C
C
B
A
D
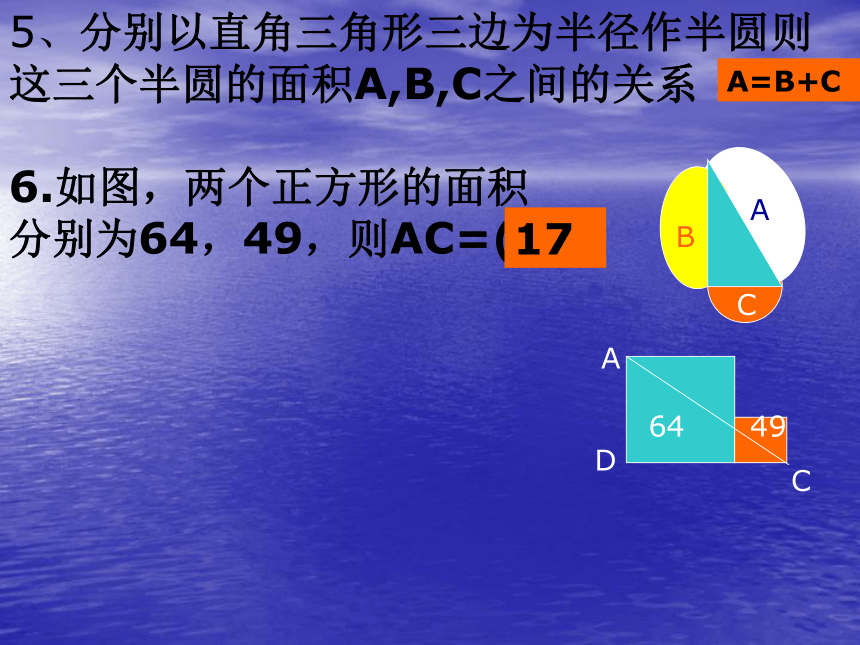
5、分别以直角三角形三边为半径作半圆则
这三个半圆的面积A,B,C之间的关系( )
6.如图,两个正方形的面积
分别为64,49,则AC=( )
A
D
C
64
49
A
B
C
A=B+C
17
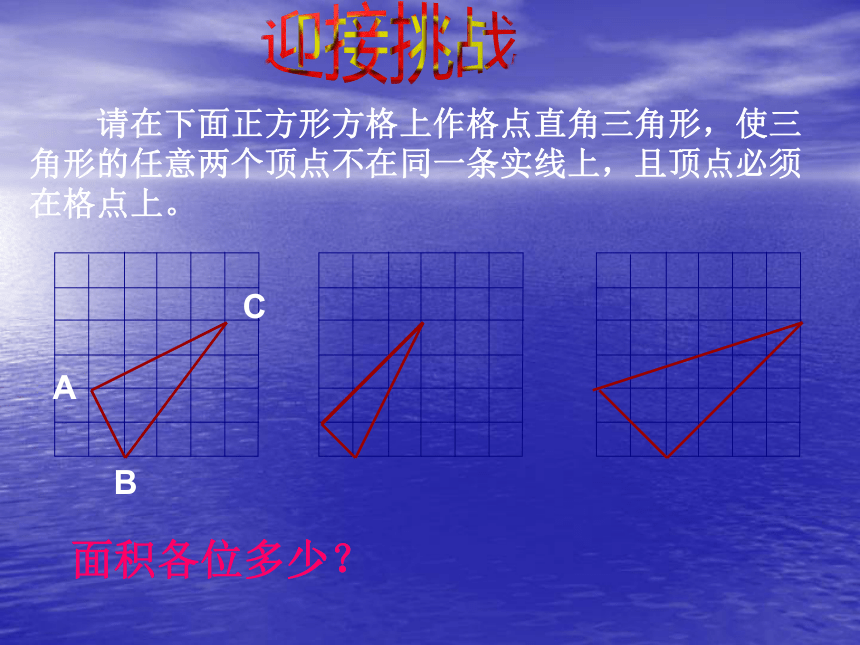
请在下面正方形方格上作格点直角三角形,使三角形的任意两个顶点不在同一条实线上,且顶点必须在格点上。
A
B
C
面积各位多少?
3、我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题。
译:有一个水池,水面是一个为10尺的正方形,在水池正中央有一根芦苇,它高出水面一尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面。这个水池的 深度与这根芦苇的长度分别是多少?
1
x
X+1
5
1、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求: (1)CF (2)EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
折叠中的计算问题
A
B
我怎么走
会最近呢
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少
三、正方体中的最值问题
例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1
A
B
分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).
C
A
B
C
2
1
例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.
A
B
A1
B1
D1
C1
①
4
2
1
AC1 =√42+32 =√25 ;
②
A
B
B1
C
A1
C1
4
1
2
AC1 =√62+12 =√37 ;
A
B1
D1
D
A1
C1
③
4
1
2
AC1 =√52+22 =√29 .
四、长方体中的最值问题
5.一长方体水池的长、宽、高分别为50cm、40cm、30cm,池中有一满池水.小亮把长度为70cm的金属棒放入水中,能否被完全淹没?说说你的理由.
综合运用
2、已知△ABC的三条边长分别为a、b、
c,且满足关系:
(a+b)2 + c2 = 3ab + c(a+b),
试判断△ABC的形状,并说明理由.
实际问题
(直角三角形边长计算)
勾股定理
勾股定理的逆定理
实际问题
(判定直角三角形)
互逆定理
1.直角三角形三边的长有什么关系 找一个实际问题并用勾股定理解决.
2.已知一个三角形的三边,你能判断它是否直角三角形吗
3.如果一个命题成立,它的逆命题一定成立吗 请举例说明.
(1)求出图形中的x
(3)在下列几组数中,能组成直角三角形的有几组?
6,8,10;5,12,13;8,40,41;
3(a-1),4(a-1),5(a-1)(a>1)
(1)已知⊿ABC中AB=AC=20,BC=24求⊿ABC的面积。
(2)已知⊿ABC中,∠C=90°,AC=4,BC=3,CD⊥AB于D,求AD,BD长。
A
B
C
C
B
A
D
5、分别以直角三角形三边为半径作半圆则
这三个半圆的面积A,B,C之间的关系( )
6.如图,两个正方形的面积
分别为64,49,则AC=( )
A
D
C
64
49
A
B
C
A=B+C
17
请在下面正方形方格上作格点直角三角形,使三角形的任意两个顶点不在同一条实线上,且顶点必须在格点上。
A
B
C
面积各位多少?
3、我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题。
译:有一个水池,水面是一个为10尺的正方形,在水池正中央有一根芦苇,它高出水面一尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面。这个水池的 深度与这根芦苇的长度分别是多少?
1
x
X+1
5
1、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求: (1)CF (2)EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
折叠中的计算问题
A
B
我怎么走
会最近呢
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少
三、正方体中的最值问题
例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1
A
B
分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).
C
A
B
C
2
1
例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.
A
B
A1
B1
D1
C1
①
4
2
1
AC1 =√42+32 =√25 ;
②
A
B
B1
C
A1
C1
4
1
2
AC1 =√62+12 =√37 ;
A
B1
D1
D
A1
C1
③
4
1
2
AC1 =√52+22 =√29 .
四、长方体中的最值问题
5.一长方体水池的长、宽、高分别为50cm、40cm、30cm,池中有一满池水.小亮把长度为70cm的金属棒放入水中,能否被完全淹没?说说你的理由.
综合运用
2、已知△ABC的三条边长分别为a、b、
c,且满足关系:
(a+b)2 + c2 = 3ab + c(a+b),
试判断△ABC的形状,并说明理由.
