勾股定理的逆定理(第一课时)16张
文档属性
| 名称 | 勾股定理的逆定理(第一课时)16张 |  | |
| 格式 | zip | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-11 15:31:17 | ||
图片预览





文档简介
(共16张PPT)
勾股定理的逆定理
(第1课时)
活动1:复习与巩固
(1)勾股定理的内容是什么
(2)求以线段a,b为直角边的直角三角形的斜边c的长:
a=3,b=4;
a=8,b=6
a=5,b=12.
①
②
③
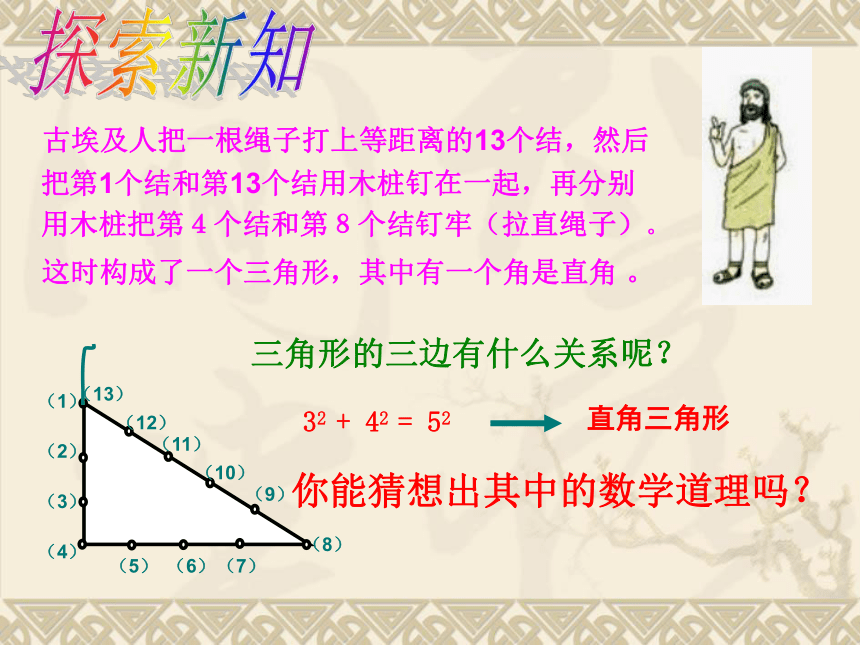
古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。
这时构成了一个三角形,其中有一个角是直角 。
三角形的三边有什么关系呢?
(1)
(3)
(2)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
你能猜想出其中的数学道理吗?
32 + 42 = 52
直角三角形
活动2 :探究
小实验:画一个△ABC, 使它的三边长分别为:
(1)、6cm、8cm、10cm (单行的同学做)
(2)、5cm、12cm、13cm (双行的同学做)
1. 问题:这两个三角形有哪些部分相同,哪些部分不同?并猜想它的最大角是什么角?
2.测量:用你的量角器分别测量一下上述各三角形的最大角的度数
3.判断:请判断一下上述你所画的三角形的形状.
4.找规律:根据上述每个三角形所给的各组边长请你找出最长边的平方与其他两边的平方和之间的关系。
5.猜想:让我们猜想一下,一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?你的猜想是_____________。
命题 2 :
如果三角形的三边长a 、 b 、 c满足
那么这个三角形是直角三角形。
分析:⑴注意命题证明的格式,首先要根据题意画出图形,然后写已知求证。
⑵如何判断一个三角形是直角三角形,现在只知道若有一个角是直角的三角形是直角三角形,从而将问题转化为如何判断一个角是直角。
⑶利用已知条件作一个直角三角形,再证明和原三角形全等,使问题得以解决。
⑷先做直角,再截取两直角边相等,利用勾股定理计算斜边A1B1=c,则通过三边对应相等的两个三角形全等可证。
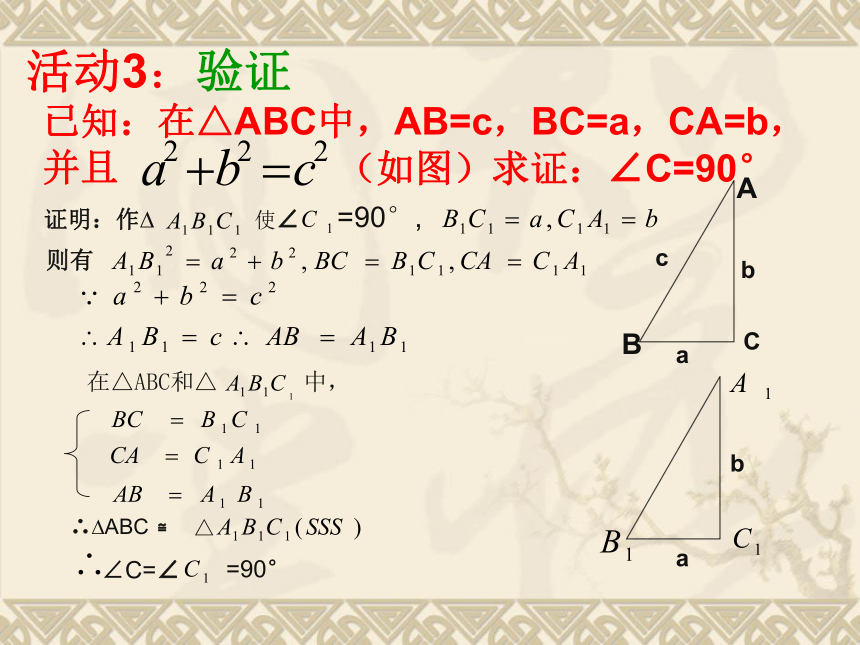
活动3:验证
已知:在△ABC中,AB=c,BC=a,CA=b,并且
A
B
b
c
a
b
证明:作
在△ABC和△
∴ ABC
∠C=∠
C
a
(如图)求证:∠C=90°
使∠
则有
中,
△
=90°
≌
=90°,
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
互逆命题
互逆定理
勾股定理的逆命题
勾股定理的逆定理
互逆定理:如果一个定理的逆命题经过证明是正确的,它
也是一个定理,称这两个定理互为逆定理。
例1 判断由线段a、 b 、 c 组成的三角形是不是直角三角形:
(1)a=15, b=8, c=17 (2) a=13, b=14,c=15
解:(1)
活动4:应用
(2)
活动5:练习
1.课本84页练习第1题
2.判断由线段a、 b 、 c 组成的三角形是不是直角三角形:
(1)a=7,b=24,c=25
(2) a=5,b=13,c=12
(3) a=4,b=5,c=6
请指出下列命题的逆命题,
(1)两直线平行,同位角相等。
(2)对顶角相等。
(3)如果两个实数相等,那么它们的绝对值相等。
(4)全等三角形的对应边相等。
能够成为直角三角形三条边长的三个正整数,称为勾股数.
以小组为单位,每位同学自己找一组
勾股数,那一组找的最快最多就算获胜。
3, 4, 5; 5,12,13;6, 8,10;
7,24,25; 8,15,17;9,40,41
9,12,15;10,24,26;……
活动6:小结
1.通过本节课的学习,你知道一个三角形的三边在数量上满足怎样的关系时,这个三角形才是直角三角形呢?
2.请你总结一下,判断一个三角形是否是直角三角形,都有哪些方法?
作业:
课本84页习题第1、2、4题
观察下列表格:
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c= ________。
勾股定理的逆定理
(第1课时)
活动1:复习与巩固
(1)勾股定理的内容是什么
(2)求以线段a,b为直角边的直角三角形的斜边c的长:
a=3,b=4;
a=8,b=6
a=5,b=12.
①
②
③
古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。
这时构成了一个三角形,其中有一个角是直角 。
三角形的三边有什么关系呢?
(1)
(3)
(2)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
你能猜想出其中的数学道理吗?
32 + 42 = 52
直角三角形
活动2 :探究
小实验:画一个△ABC, 使它的三边长分别为:
(1)、6cm、8cm、10cm (单行的同学做)
(2)、5cm、12cm、13cm (双行的同学做)
1. 问题:这两个三角形有哪些部分相同,哪些部分不同?并猜想它的最大角是什么角?
2.测量:用你的量角器分别测量一下上述各三角形的最大角的度数
3.判断:请判断一下上述你所画的三角形的形状.
4.找规律:根据上述每个三角形所给的各组边长请你找出最长边的平方与其他两边的平方和之间的关系。
5.猜想:让我们猜想一下,一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?你的猜想是_____________。
命题 2 :
如果三角形的三边长a 、 b 、 c满足
那么这个三角形是直角三角形。
分析:⑴注意命题证明的格式,首先要根据题意画出图形,然后写已知求证。
⑵如何判断一个三角形是直角三角形,现在只知道若有一个角是直角的三角形是直角三角形,从而将问题转化为如何判断一个角是直角。
⑶利用已知条件作一个直角三角形,再证明和原三角形全等,使问题得以解决。
⑷先做直角,再截取两直角边相等,利用勾股定理计算斜边A1B1=c,则通过三边对应相等的两个三角形全等可证。
活动3:验证
已知:在△ABC中,AB=c,BC=a,CA=b,并且
A
B
b
c
a
b
证明:作
在△ABC和△
∴ ABC
∠C=∠
C
a
(如图)求证:∠C=90°
使∠
则有
中,
△
=90°
≌
=90°,
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
互逆命题
互逆定理
勾股定理的逆命题
勾股定理的逆定理
互逆定理:如果一个定理的逆命题经过证明是正确的,它
也是一个定理,称这两个定理互为逆定理。
例1 判断由线段a、 b 、 c 组成的三角形是不是直角三角形:
(1)a=15, b=8, c=17 (2) a=13, b=14,c=15
解:(1)
活动4:应用
(2)
活动5:练习
1.课本84页练习第1题
2.判断由线段a、 b 、 c 组成的三角形是不是直角三角形:
(1)a=7,b=24,c=25
(2) a=5,b=13,c=12
(3) a=4,b=5,c=6
请指出下列命题的逆命题,
(1)两直线平行,同位角相等。
(2)对顶角相等。
(3)如果两个实数相等,那么它们的绝对值相等。
(4)全等三角形的对应边相等。
能够成为直角三角形三条边长的三个正整数,称为勾股数.
以小组为单位,每位同学自己找一组
勾股数,那一组找的最快最多就算获胜。
3, 4, 5; 5,12,13;6, 8,10;
7,24,25; 8,15,17;9,40,41
9,12,15;10,24,26;……
活动6:小结
1.通过本节课的学习,你知道一个三角形的三边在数量上满足怎样的关系时,这个三角形才是直角三角形呢?
2.请你总结一下,判断一个三角形是否是直角三角形,都有哪些方法?
作业:
课本84页习题第1、2、4题
观察下列表格:
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c= ________。
