勾股定理有关证明(42张)
文档属性
| 名称 | 勾股定理有关证明(42张) |  | |
| 格式 | zip | ||
| 文件大小 | 313.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-11 15:31:28 | ||
图片预览





文档简介
(共42张PPT)
勾股定理的有关证明
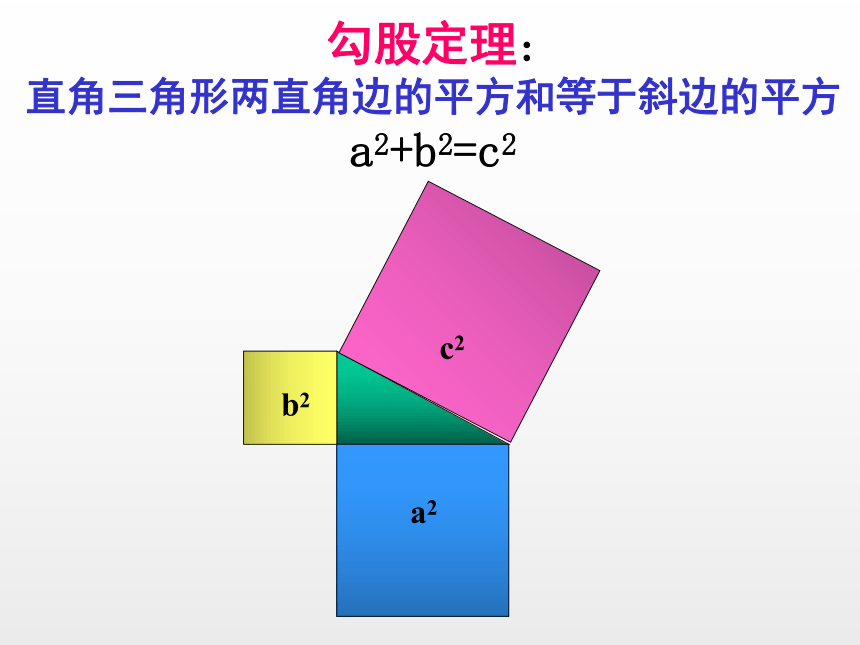
勾股定理:
直角三角形两直角边的平方和等于斜边的平方
a2+b2=c2
b2
c2
a2
1
1
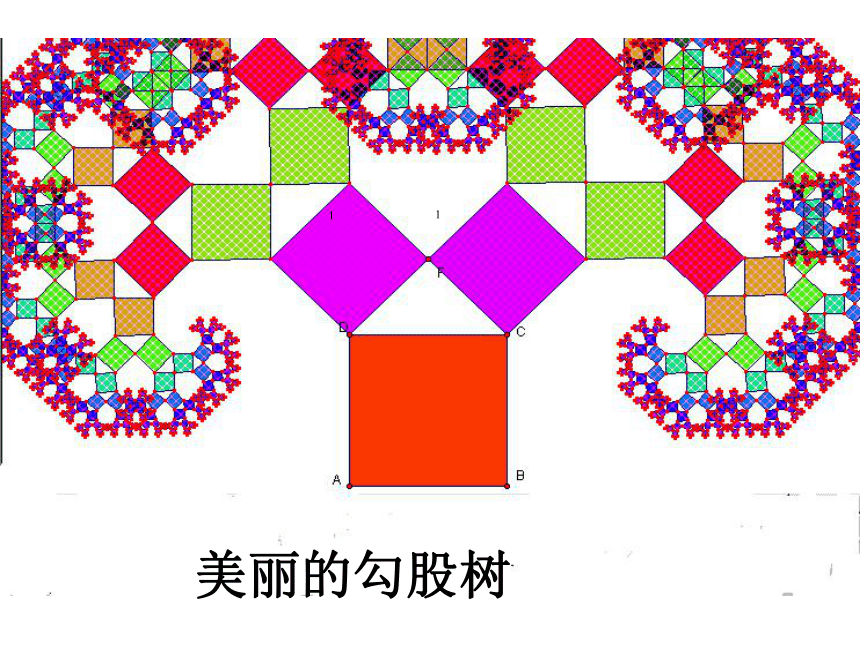
美丽的勾股树
2002年,在北京举行的国际数学家大会会标
赵爽的“弦图”
早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”
思考:你能验证吗?
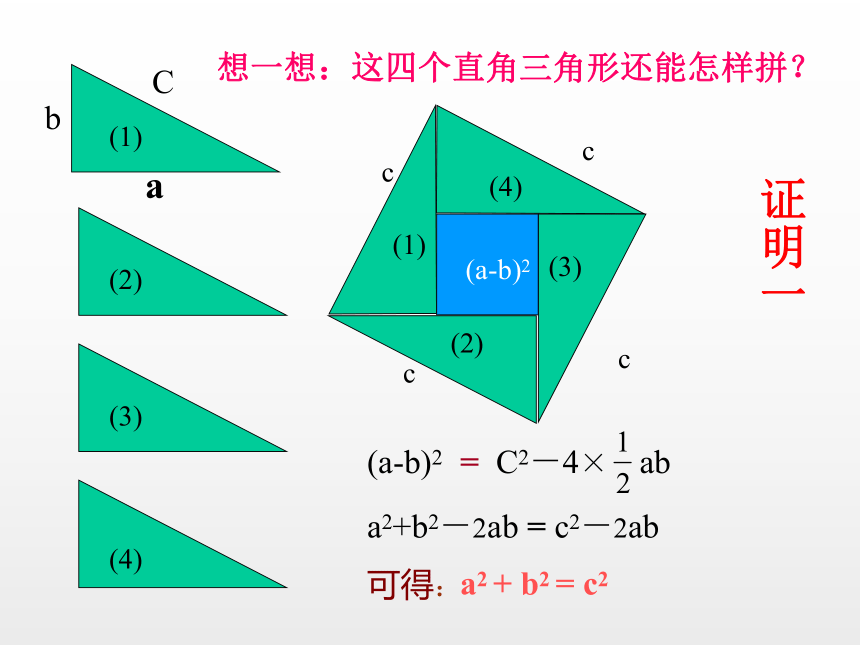
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
(a-b)2
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
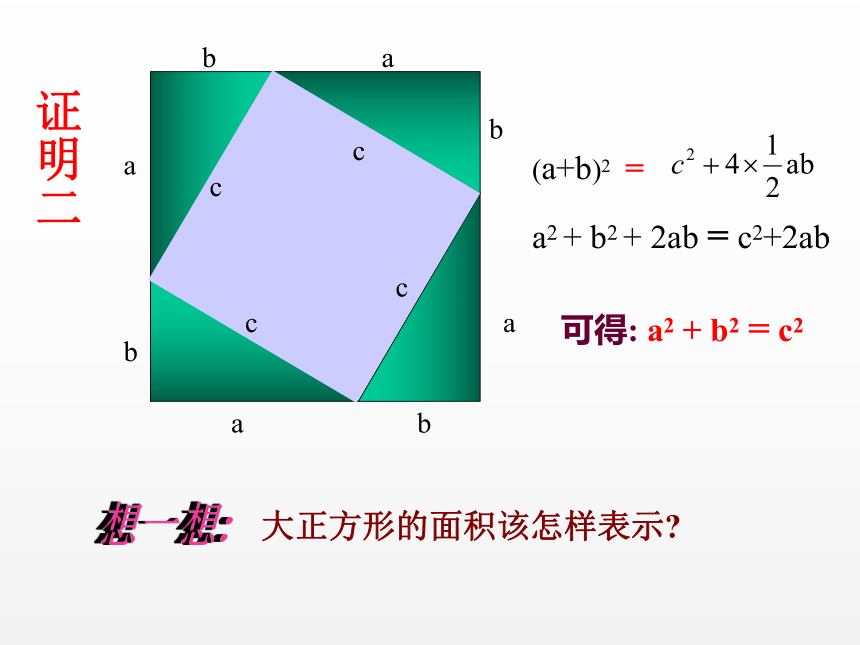
b
C
a
想一想:这四个直角三角形还能怎样拼?
证明一
b
a
b
a
b
a
b
a
c
c
c
c
大正方形的面积该怎样表示
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明二
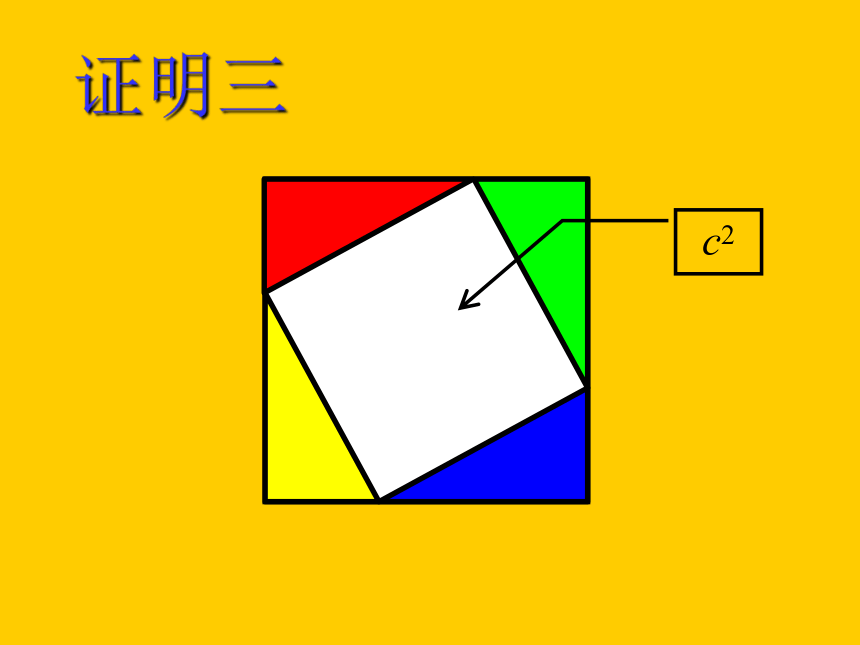
证明三
c2
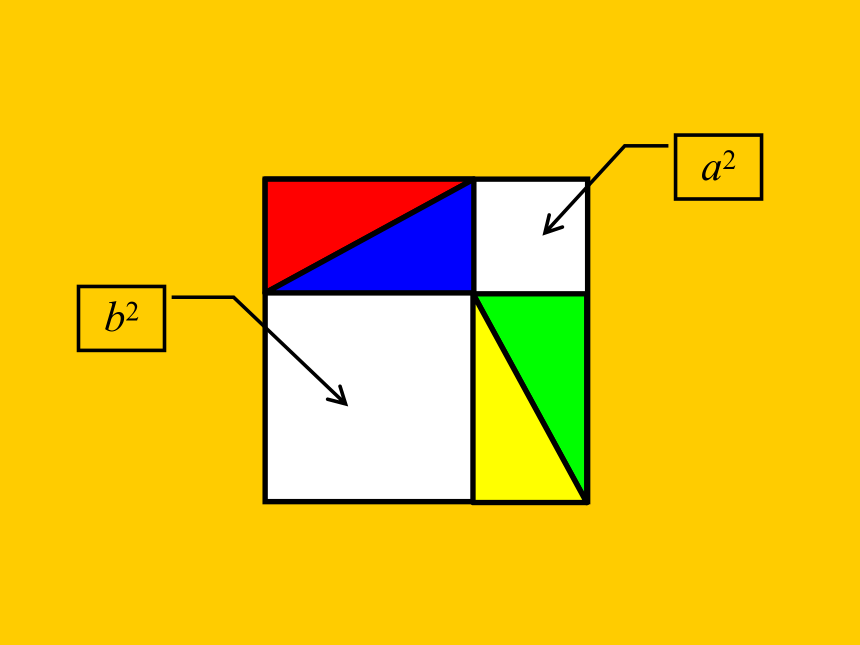
a2
b2
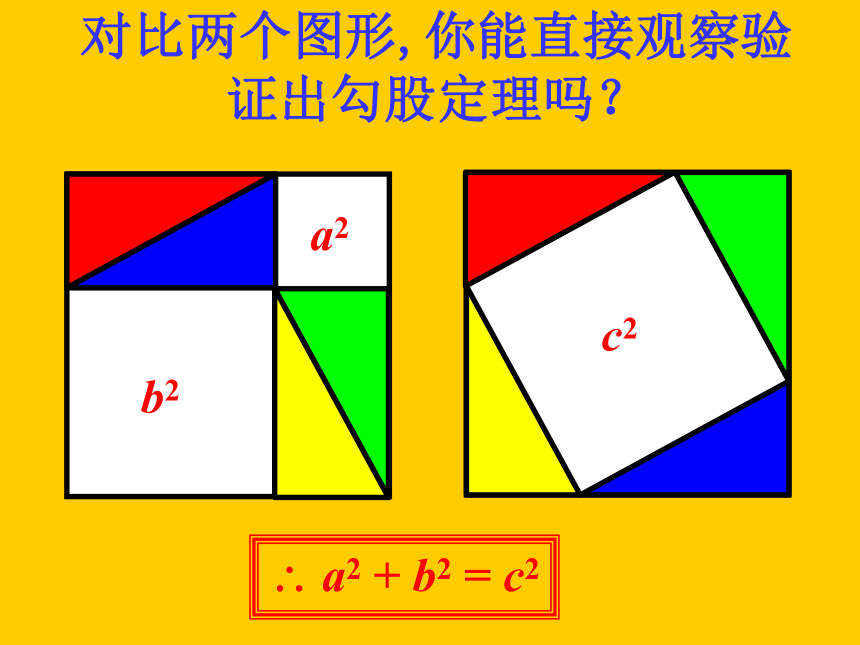
a2 + b2 = c2
a2
b2
a2
c2
对比两个图形,你能直接观察验证出勾股定理吗?
a
证明六 印度婆什迦羅的證明
c
c2 = b2 + a2
b
证明七 “总统”证法
(a + b)(b + a) = c2 + 2× ab
a2 + 2ab + b2 = c2 +2 ab
a2 + b2 = c2
a
a
b
b
c
c
证明八
证明八
证明八
证明八
证明八
a2
b2
证明九
证明九
证明九
证明九
证明九
c2
a2 + b2 = c2
证明九
证明九
拼图游戏
证明九
拼图游戏
无字证明
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
无字证明
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
证明十
I
II
III
注意:
面积 I :面积II :面积III = a2 : b2 : c2
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
由此得,面积 I + 面积 II = 面积 III
因此,a2 + b2 = c2 。
证明十
在从“面积到乘法公式”一章的学习中,我们把几个图形拼成一个新的图形,通过图形面积的计算得到了许多有用的式子。这节课同样地我们用多种方法拼图验证了勾股定理,你有什么感受?
例 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A 2、4、6
C 4、6、8
B
试一试:
B 6、8、10
D 8、10、12
勾股定理的有关证明
勾股定理:
直角三角形两直角边的平方和等于斜边的平方
a2+b2=c2
b2
c2
a2
1
1
美丽的勾股树
2002年,在北京举行的国际数学家大会会标
赵爽的“弦图”
早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”
思考:你能验证吗?
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
(a-b)2
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
b
C
a
想一想:这四个直角三角形还能怎样拼?
证明一
b
a
b
a
b
a
b
a
c
c
c
c
大正方形的面积该怎样表示
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明二
证明三
c2
a2
b2
a2 + b2 = c2
a2
b2
a2
c2
对比两个图形,你能直接观察验证出勾股定理吗?
a
证明六 印度婆什迦羅的證明
c
c2 = b2 + a2
b
证明七 “总统”证法
(a + b)(b + a) = c2 + 2× ab
a2 + 2ab + b2 = c2 +2 ab
a2 + b2 = c2
a
a
b
b
c
c
证明八
证明八
证明八
证明八
证明八
a2
b2
证明九
证明九
证明九
证明九
证明九
c2
a2 + b2 = c2
证明九
证明九
拼图游戏
证明九
拼图游戏
无字证明
青出
朱方
青方
朱入
朱出
青入
青入
青出
青出
a
b
c
无字证明
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
证明十
I
II
III
注意:
面积 I :面积II :面积III = a2 : b2 : c2
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
I
II
III
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
证明十
注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2
由此得,面积 I + 面积 II = 面积 III
因此,a2 + b2 = c2 。
证明十
在从“面积到乘法公式”一章的学习中,我们把几个图形拼成一个新的图形,通过图形面积的计算得到了许多有用的式子。这节课同样地我们用多种方法拼图验证了勾股定理,你有什么感受?
例 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A 2、4、6
C 4、6、8
B
试一试:
B 6、8、10
D 8、10、12
