人教版高中三年级利用法向量求点到平面的距离
文档属性
| 名称 | 人教版高中三年级利用法向量求点到平面的距离 |

|
|
| 格式 | zip | ||
| 文件大小 | 447.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-11 00:00:00 | ||
图片预览







文档简介
(共40张PPT)
欢
迎
指
导
!
利用法向量求
点到平面的距离
一、复习引入
三、归纳小结
五、反馈总结
二、探索新知
四、巩固迁移
六、反思作业
问题1
则
设
一、复习引入
若A(x1 , y1 , z1), B(x2 , y2 , z2) , 则
AB
=
(x2-x1, y2-y1, z2-z1)
(2) 若M(x,y,z)是线段AB的中点,则
(1)
问题2
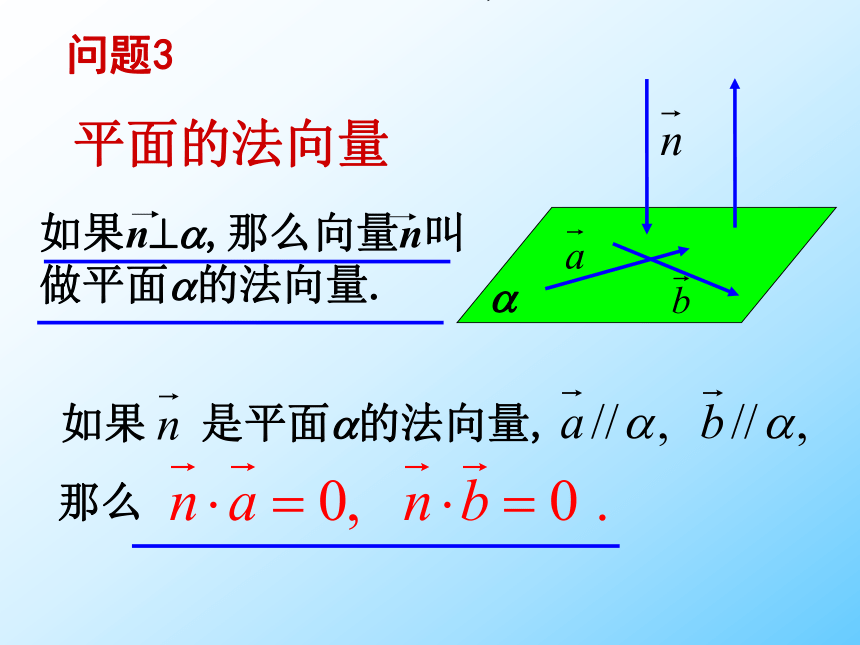
平面的法向量
如果n ,那么向量n叫做平面 的法向量.
问题3
如果 是平面 的法向量,
那么
②向量a在轴l上或在e方向(e是l上同方向的单位向量)上的投影:
l
O
A
B
问题4
①设
则
l
B
A
O
A
o
B
二、探索新知
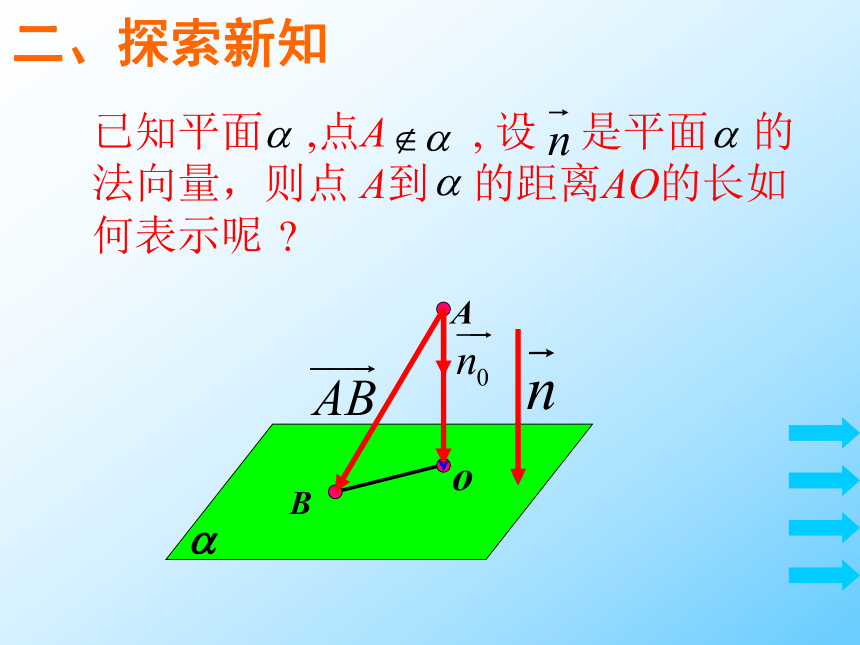
已知平面 ,点A , 设 是平面 的
法向量,则点 A到 的距离AO的长如
何表示呢
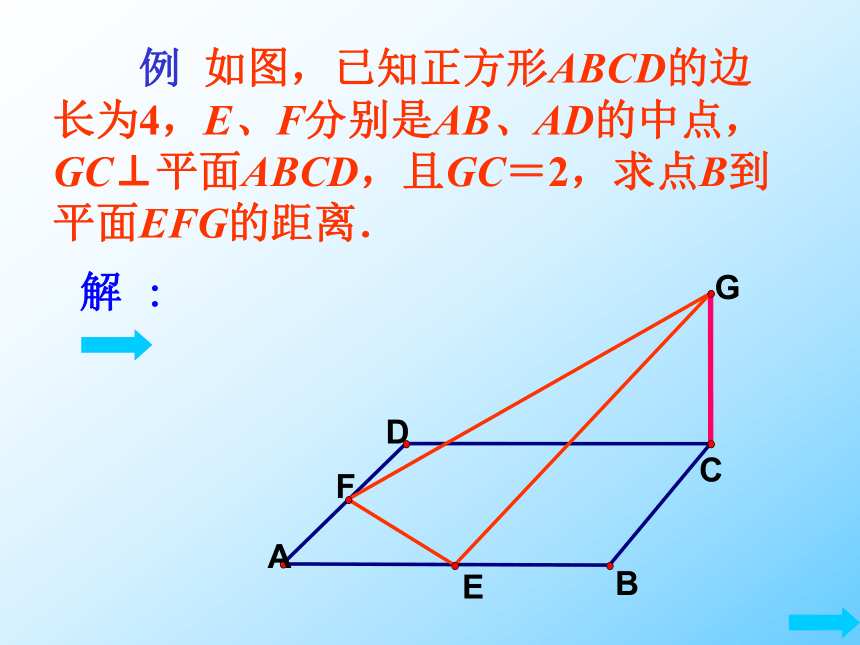
例 如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
D
C
A
B
G
F
E
解 :
三、归纳小结
用法向量求点到平面距离的一般过程是:
(1)建立适当的空间直角坐标系,求出需要的点的坐标;
(2)求出平面的法向量 ;
(3)作向量 (点A为平面外一定点,点B为平面内任一点);
(4)求向量 在法向量 上的射影的长度
( 其中 是与 同方向的单位法向量)
说明:
利用法向量求点到平面的距离,常常不必作出垂线段,利用平面的法向量,把点A到平面 的距离 看成点A与平面 内的任意一点B所构成的向量 在法向量 方向上的射影的长度,此种方法具有程序化,不需 技巧,可以人人学会。
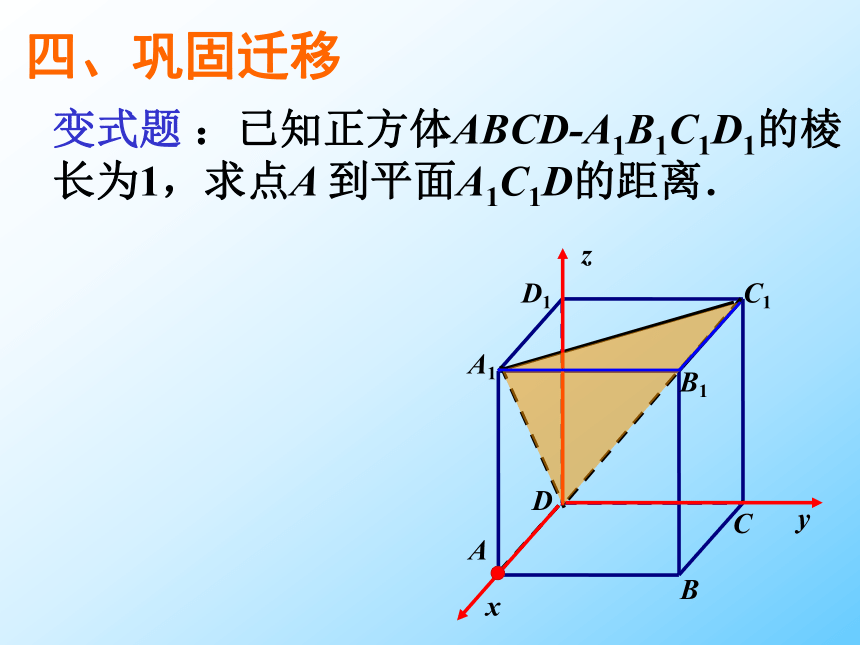
变式题 :已知正方体ABCD-A1B1C1D1的棱长为1,求点A 到平面A1C1D的距离.
B
C
C1
D
B1
A1
D1
A
x
z
四、巩固迁移
y
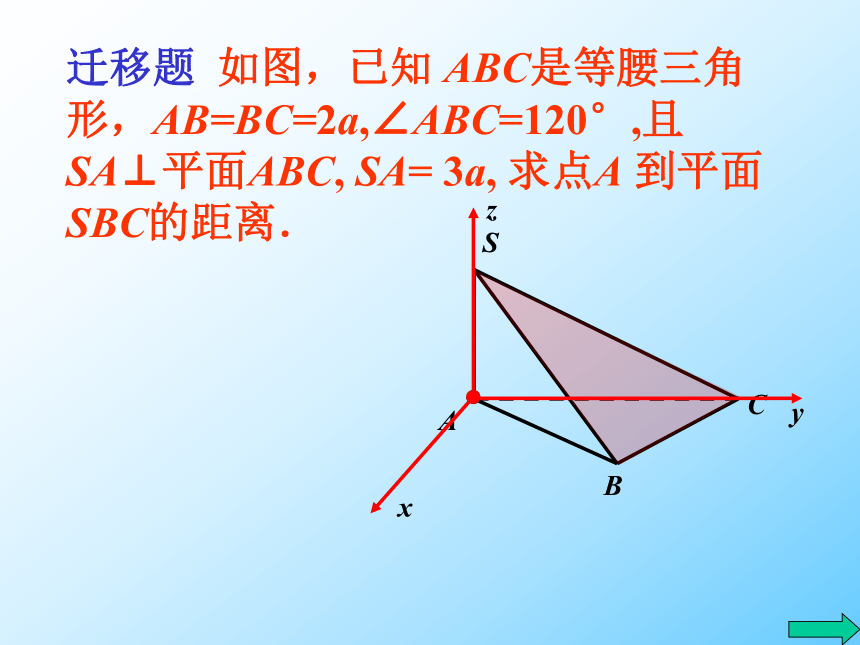
迁移题 如图,已知 ABC是等腰三角形,AB=BC=2a,∠ABC=120°,且SA⊥平面ABC, SA= 3a, 求点A 到平面SBC的距离.
A
C
S
B
x
y
z
五、反馈总结
(2)在求法向量的过程中,解方程组之后,
不能令x或y或z 为0;
(1)建立空间直角坐标系是关键,求点的
坐标要准确;
(3)点到平面的距离公式 中,
点A为平面 外一定点,点B为平面 内任一点, 为平面 的法向量.
(4)公式实质为
六、反思与作业
在棱长为2的
正方体 中,
E、F分别是棱
的中点. 试用向量方法
求点 到平面EFBD的距离.
反思: 通过本节课谈谈自己的收获
是什么
作业:
B
C
C1
D
B1
A1
D1
A
E
F
在棱长为2的
正方体 中,
E、F分别是棱
的中点. 试用向量方法
求点 到平面EFBD的距离.
作业:
B
C
C1
D
B1
A1
D1
A
E
F
欢迎指导 谢谢!
欢 迎 指 导
谢谢!
A
o
B
即点 A到平面 的距离为
在直角三角形AOB中,得
由
其中, 是平面 的
单位法向量
A
o
B
点A到平面 的距离 可以看成 (点B是平面 内任一点)在平面 的法向量 的方向上的射影的长度:
其中, 是平面 的
单位法向量
A
o
B
重点理解:
B'
1
A
o
B
A
B
d
B'
A'
即向量 在法向量 上的射影的长度
例 如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
D
C
A
B
G
F
E
解 :
三、归纳小结
用法向量求点到平面距离的一般过程是:
(1)建立适当的空间直角坐标系,求出需要的点的坐标;
(2)求出平面的法向量 ;
(3)作向量 (点A为平面外一定点,点B为平面内任一点);
(4)求向量 在法向量 上的射影的长度
( 其中 是与 同方向的单位法向量)
说明:
利用法向量求点到平面的距离,常常不必作出垂线段,利用平面的法向量,把点A到平面 的距离 看成点A与平面 内的任意一点B所构成的向量 在法向量 方向上的射影的长度,此种方法具有程序化,不需 技巧,可以人人学会。
变式题 :已知正方体ABCD-A1B1C1D1的棱长为1,求点A 到平面A1C1D的距离.
B
C
C1
D
B1
A1
D1
A
x
z
四、巩固迁移
y
延伸迁移 如图,已知 ABC是等腰三角形,AB=BC=2a,∠ABC=120°,且SA⊥平面ABC, SA= 3a, 求点A 到平面SBC的距离.
A
C
S
B
x
y
z
五、反馈总结
(2)在求法向量的过程中,解方程组之后,
不能令x或y或z 为0;
(1)建立空间直角坐标系是关键,求点的
坐标要准确;
(3)点到平面的距离公式 中,
点A为平面 外一定点,点B为平面 内任一点, 为平面 的法向量.
(4)公式还可化为
六、反思与作业
在棱长为2的
正方体 中,
E、F分别是棱
的中点. 试用向量方法
求点 到平面EFBD的距离.
反思: 通过本节课谈
谈自己的收获是什么
作业:
谢谢指导!
再见.
B
C
C1
D
B1
A1
D1
A
E
F
D
C
A
B
G
F
E
y
z
如图建立空间坐标系,
G(0,4,2),
F(2, 0, 0)
,E(4, 2, 0)
,
∵
∴
,则
∴
则
设平面的法向量为
解:
x
返回
∴x=-y,z=-3y.
令y=-1,
D
A
B
C
G
F
E
x
y
z
解:如图建立空间直角坐标系,则G(0,O,2),F(4,2,O),E(2,4,0),B(0,4,O).
=(2,-2,0),
=(2,4,-2),
设面GEF的法向量为
= 0 ,
=0 ,
∴ 2x-2y=0,2x+4y-2z=0,
∴x=y,z=3y.
=(1,1,3).
∴点B到面GEF的距离为
返
回
令y=1,则
=(2,0,0).
x
y
z
法向量的应用:点到面的距离
例2:已知棱长为1的正方体ABCD-A1B1C1D1,E,F分别是B1C1和C1D1的中点,求点A1到平面BDEF的距离。
F
E
D1
C1
B1
A1
D
C
B
A
A
B
d
B'
A'
即向量 在法向量 上的射影的长度
教师引导,学生总结:
法一:设 是平面 的法向量,在 内取一点B, 则点 A到 的距离
法二:设 于O,利用 和点O在 内的向量表示,可确定点O的位置,进而求出 .
B
A
O
B
A
说明:
用向量法求点到平面的距离,常常不必作出垂线段,利用平面的法向量,把点A到平面 的距离 看成点A与平面 内的任意一点B所构成的向量 在法向量 方向上的射影的长度,此种方法具有程序化,不需技巧,可以人人学会。
点到平面的距离
A
o
B
即点 A到平面 的距离为
在直角三角形AOB中,得
由
点到平面的距离
A
o
B
已知平面 ,点A , 设 是平面 的法向量,过A作AO⊥ 于点O,则 ,在 内取一点B, 则点 A到 的距离AO的长如何表示呢
在直角三角形AOB中,由
得
点到平面的距离
A
o
B
点到平面的距离
A
o
B
其中,点B为平面 内任一点, 为平面 的法向量.
已知平面 ,点A , 设 是平面 的法向量,过A作AO⊥ 于点O,则 ,在 内取一点B, 则点 A到 的距离AO的长如何表示呢
即点 A到平面 的距离为
点A到平面 的距离 可以看成 (点B是平面 内任一点)在平面 的法向量 的方向上的射影的长度:
其中, 是平面 的
单位法向量
A
o
B
重点理解:
五、归纳总结
利用向量方法求解空间距离问题,可以回避此类问题中大量的作图、证明等步骤,而转化为向量间的计算问题 运用平面的法向量求立体几何中的距离问题时,首先要建立适当的坐标系,进而将向量坐标化,求出平面的法向量,再代入公式求解。需要注意的是:
(1)在求法向量的过程中,解方程组之后,不能令x或y或z 为0;
(2)建立空间直角坐标系是关键,求点的坐标要准确;
(3)对点到平面距离公式的推导过程要认真领会,
掌握公式: , 并会应用.
欢
迎
指
导
!
利用法向量求
点到平面的距离
一、复习引入
三、归纳小结
五、反馈总结
二、探索新知
四、巩固迁移
六、反思作业
问题1
则
设
一、复习引入
若A(x1 , y1 , z1), B(x2 , y2 , z2) , 则
AB
=
(x2-x1, y2-y1, z2-z1)
(2) 若M(x,y,z)是线段AB的中点,则
(1)
问题2
平面的法向量
如果n ,那么向量n叫做平面 的法向量.
问题3
如果 是平面 的法向量,
那么
②向量a在轴l上或在e方向(e是l上同方向的单位向量)上的投影:
l
O
A
B
问题4
①设
则
l
B
A
O
A
o
B
二、探索新知
已知平面 ,点A , 设 是平面 的
法向量,则点 A到 的距离AO的长如
何表示呢
例 如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
D
C
A
B
G
F
E
解 :
三、归纳小结
用法向量求点到平面距离的一般过程是:
(1)建立适当的空间直角坐标系,求出需要的点的坐标;
(2)求出平面的法向量 ;
(3)作向量 (点A为平面外一定点,点B为平面内任一点);
(4)求向量 在法向量 上的射影的长度
( 其中 是与 同方向的单位法向量)
说明:
利用法向量求点到平面的距离,常常不必作出垂线段,利用平面的法向量,把点A到平面 的距离 看成点A与平面 内的任意一点B所构成的向量 在法向量 方向上的射影的长度,此种方法具有程序化,不需 技巧,可以人人学会。
变式题 :已知正方体ABCD-A1B1C1D1的棱长为1,求点A 到平面A1C1D的距离.
B
C
C1
D
B1
A1
D1
A
x
z
四、巩固迁移
y
迁移题 如图,已知 ABC是等腰三角形,AB=BC=2a,∠ABC=120°,且SA⊥平面ABC, SA= 3a, 求点A 到平面SBC的距离.
A
C
S
B
x
y
z
五、反馈总结
(2)在求法向量的过程中,解方程组之后,
不能令x或y或z 为0;
(1)建立空间直角坐标系是关键,求点的
坐标要准确;
(3)点到平面的距离公式 中,
点A为平面 外一定点,点B为平面 内任一点, 为平面 的法向量.
(4)公式实质为
六、反思与作业
在棱长为2的
正方体 中,
E、F分别是棱
的中点. 试用向量方法
求点 到平面EFBD的距离.
反思: 通过本节课谈谈自己的收获
是什么
作业:
B
C
C1
D
B1
A1
D1
A
E
F
在棱长为2的
正方体 中,
E、F分别是棱
的中点. 试用向量方法
求点 到平面EFBD的距离.
作业:
B
C
C1
D
B1
A1
D1
A
E
F
欢迎指导 谢谢!
欢 迎 指 导
谢谢!
A
o
B
即点 A到平面 的距离为
在直角三角形AOB中,得
由
其中, 是平面 的
单位法向量
A
o
B
点A到平面 的距离 可以看成 (点B是平面 内任一点)在平面 的法向量 的方向上的射影的长度:
其中, 是平面 的
单位法向量
A
o
B
重点理解:
B'
1
A
o
B
A
B
d
B'
A'
即向量 在法向量 上的射影的长度
例 如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
D
C
A
B
G
F
E
解 :
三、归纳小结
用法向量求点到平面距离的一般过程是:
(1)建立适当的空间直角坐标系,求出需要的点的坐标;
(2)求出平面的法向量 ;
(3)作向量 (点A为平面外一定点,点B为平面内任一点);
(4)求向量 在法向量 上的射影的长度
( 其中 是与 同方向的单位法向量)
说明:
利用法向量求点到平面的距离,常常不必作出垂线段,利用平面的法向量,把点A到平面 的距离 看成点A与平面 内的任意一点B所构成的向量 在法向量 方向上的射影的长度,此种方法具有程序化,不需 技巧,可以人人学会。
变式题 :已知正方体ABCD-A1B1C1D1的棱长为1,求点A 到平面A1C1D的距离.
B
C
C1
D
B1
A1
D1
A
x
z
四、巩固迁移
y
延伸迁移 如图,已知 ABC是等腰三角形,AB=BC=2a,∠ABC=120°,且SA⊥平面ABC, SA= 3a, 求点A 到平面SBC的距离.
A
C
S
B
x
y
z
五、反馈总结
(2)在求法向量的过程中,解方程组之后,
不能令x或y或z 为0;
(1)建立空间直角坐标系是关键,求点的
坐标要准确;
(3)点到平面的距离公式 中,
点A为平面 外一定点,点B为平面 内任一点, 为平面 的法向量.
(4)公式还可化为
六、反思与作业
在棱长为2的
正方体 中,
E、F分别是棱
的中点. 试用向量方法
求点 到平面EFBD的距离.
反思: 通过本节课谈
谈自己的收获是什么
作业:
谢谢指导!
再见.
B
C
C1
D
B1
A1
D1
A
E
F
D
C
A
B
G
F
E
y
z
如图建立空间坐标系,
G(0,4,2),
F(2, 0, 0)
,E(4, 2, 0)
,
∵
∴
,则
∴
则
设平面的法向量为
解:
x
返回
∴x=-y,z=-3y.
令y=-1,
D
A
B
C
G
F
E
x
y
z
解:如图建立空间直角坐标系,则G(0,O,2),F(4,2,O),E(2,4,0),B(0,4,O).
=(2,-2,0),
=(2,4,-2),
设面GEF的法向量为
= 0 ,
=0 ,
∴ 2x-2y=0,2x+4y-2z=0,
∴x=y,z=3y.
=(1,1,3).
∴点B到面GEF的距离为
返
回
令y=1,则
=(2,0,0).
x
y
z
法向量的应用:点到面的距离
例2:已知棱长为1的正方体ABCD-A1B1C1D1,E,F分别是B1C1和C1D1的中点,求点A1到平面BDEF的距离。
F
E
D1
C1
B1
A1
D
C
B
A
A
B
d
B'
A'
即向量 在法向量 上的射影的长度
教师引导,学生总结:
法一:设 是平面 的法向量,在 内取一点B, 则点 A到 的距离
法二:设 于O,利用 和点O在 内的向量表示,可确定点O的位置,进而求出 .
B
A
O
B
A
说明:
用向量法求点到平面的距离,常常不必作出垂线段,利用平面的法向量,把点A到平面 的距离 看成点A与平面 内的任意一点B所构成的向量 在法向量 方向上的射影的长度,此种方法具有程序化,不需技巧,可以人人学会。
点到平面的距离
A
o
B
即点 A到平面 的距离为
在直角三角形AOB中,得
由
点到平面的距离
A
o
B
已知平面 ,点A , 设 是平面 的法向量,过A作AO⊥ 于点O,则 ,在 内取一点B, 则点 A到 的距离AO的长如何表示呢
在直角三角形AOB中,由
得
点到平面的距离
A
o
B
点到平面的距离
A
o
B
其中,点B为平面 内任一点, 为平面 的法向量.
已知平面 ,点A , 设 是平面 的法向量,过A作AO⊥ 于点O,则 ,在 内取一点B, 则点 A到 的距离AO的长如何表示呢
即点 A到平面 的距离为
点A到平面 的距离 可以看成 (点B是平面 内任一点)在平面 的法向量 的方向上的射影的长度:
其中, 是平面 的
单位法向量
A
o
B
重点理解:
五、归纳总结
利用向量方法求解空间距离问题,可以回避此类问题中大量的作图、证明等步骤,而转化为向量间的计算问题 运用平面的法向量求立体几何中的距离问题时,首先要建立适当的坐标系,进而将向量坐标化,求出平面的法向量,再代入公式求解。需要注意的是:
(1)在求法向量的过程中,解方程组之后,不能令x或y或z 为0;
(2)建立空间直角坐标系是关键,求点的坐标要准确;
(3)对点到平面距离公式的推导过程要认真领会,
掌握公式: , 并会应用.
