等腰三角形导学案(4课时)
图片预览

文档简介
等腰三角形导学案第一课时
教学目标:1、理解等腰三角形的性质和判定定理
2、利用定理证明解决实际问题
任务一:
自主学习:(独立完成,组内交流,课堂展示)
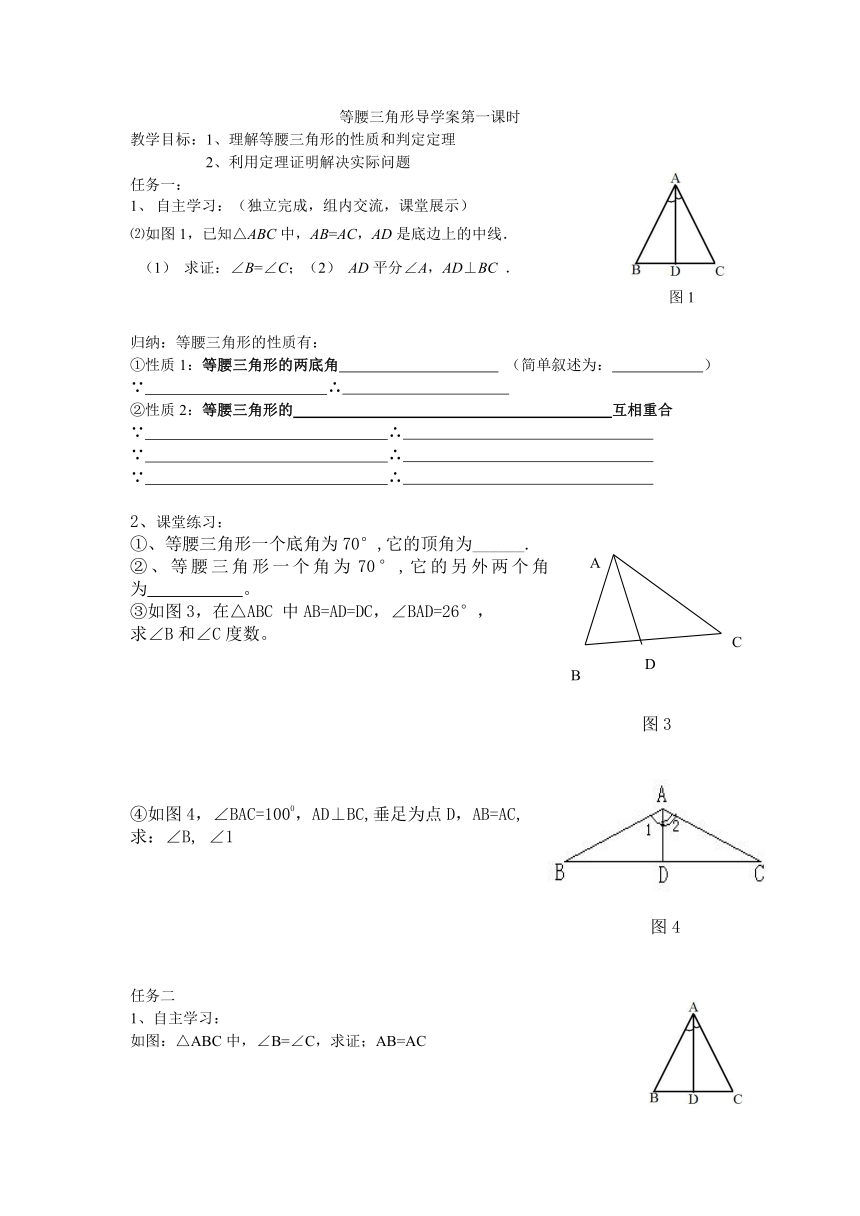
⑵如图1,已知△ABC中,AB=AC,AD是底边上的中线.
(1) 求证:∠B=∠C;(2) AD平分∠A,AD⊥BC .
图1
归纳:等腰三角形的性质有:
①性质1:等腰三角形的两底角 (简单叙述为: )
∵ ∴
②性质2:等腰三角形的 互相重合
∵ ∴
∵ ∴
∵ ∴
课堂练习:
①、等腰三角形一个底角为70°,它的顶角为______.
②、等腰三角形一个角为70°,它的另外两个角为 。
③如图3,在△ABC 中AB=AD=DC,∠BAD=26°,
求∠B和∠C度数。
图3
④如图4,∠BAC=1000,AD⊥BC,垂足为点D,AB=AC,
求:∠B, ∠1
图4
任务二
1、自主学习:
如图:△ABC中,∠B=∠C,求证;AB=AC
归纳:等腰三角形判定定理: (简单叙述为: )
∵ ∴
思考:要证明△ABC是等腰三角形,你都有哪些方法?
巩固练习:
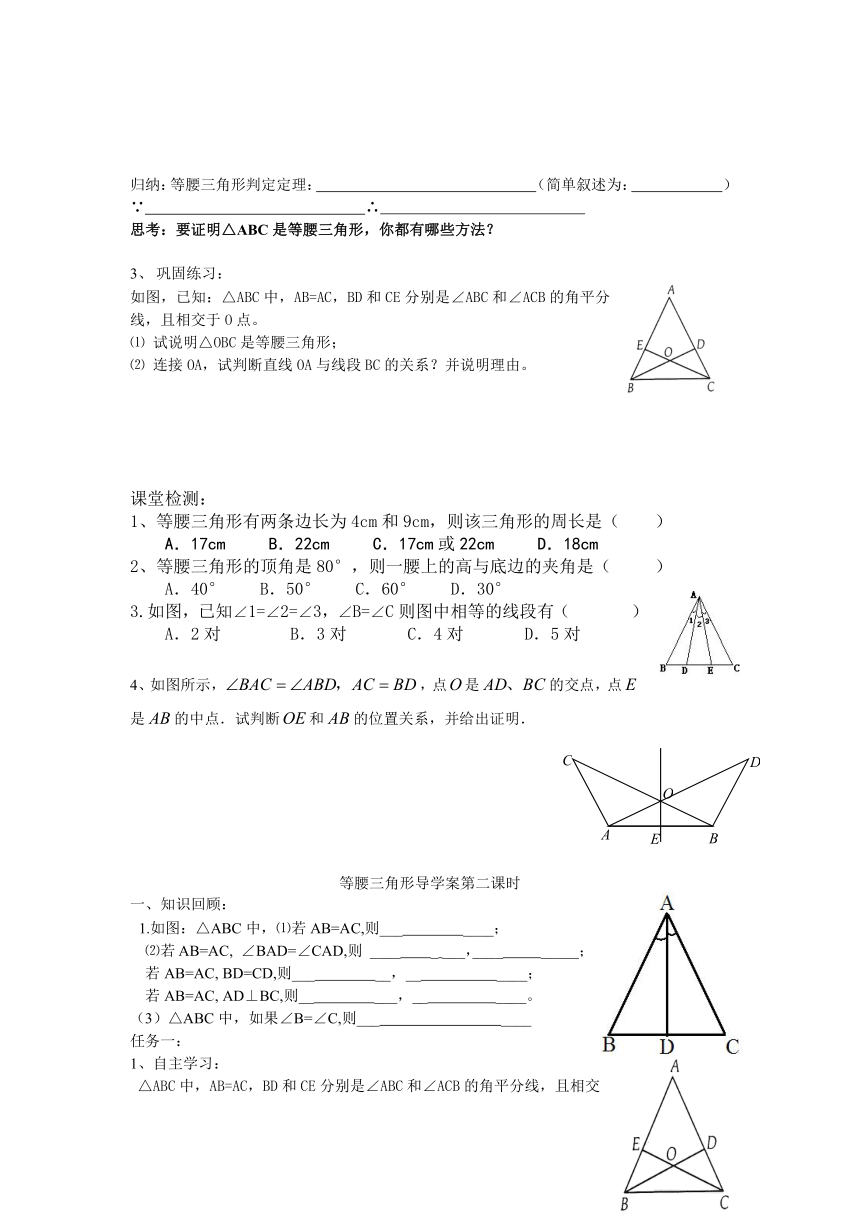
如图,已知:△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且相交于O点。
⑴ 试说明△OBC是等腰三角形;
⑵ 连接OA,试判断直线OA与线段BC的关系?并说明理由。
课堂检测:
1、等腰三角形有两条边长为4cm和9cm,则该三角形的周长是( )
A.17cm B.22cm C.17cm或22cm D.18cm
2、等腰三角形的顶角是80°,则一腰上的高与底边的夹角是( )
A.40° B.50° C.60° D.30°
3.如图,已知∠1=∠2=∠3,∠B=∠C则图中相等的线段有( )
A.2对 B.3对 C.4对 D.5对
4、如图所示,,点是的交点,点是的中点.试判断和的位置关系,并给出证明.
等腰三角形导学案第二课时
知识回顾:
1.如图:△ABC中,⑴若AB=AC,则___ ____;
⑵若AB=AC, ∠BAD=∠CAD,则 ____ _ ___,____ _____;
若AB=AC, BD=CD,则___ __,__ ____;
若AB=AC, AD⊥BC,则__ ___,__ ____。
(3)△ABC中,如果∠B=∠C,则___ ____
任务一:
1、自主学习:
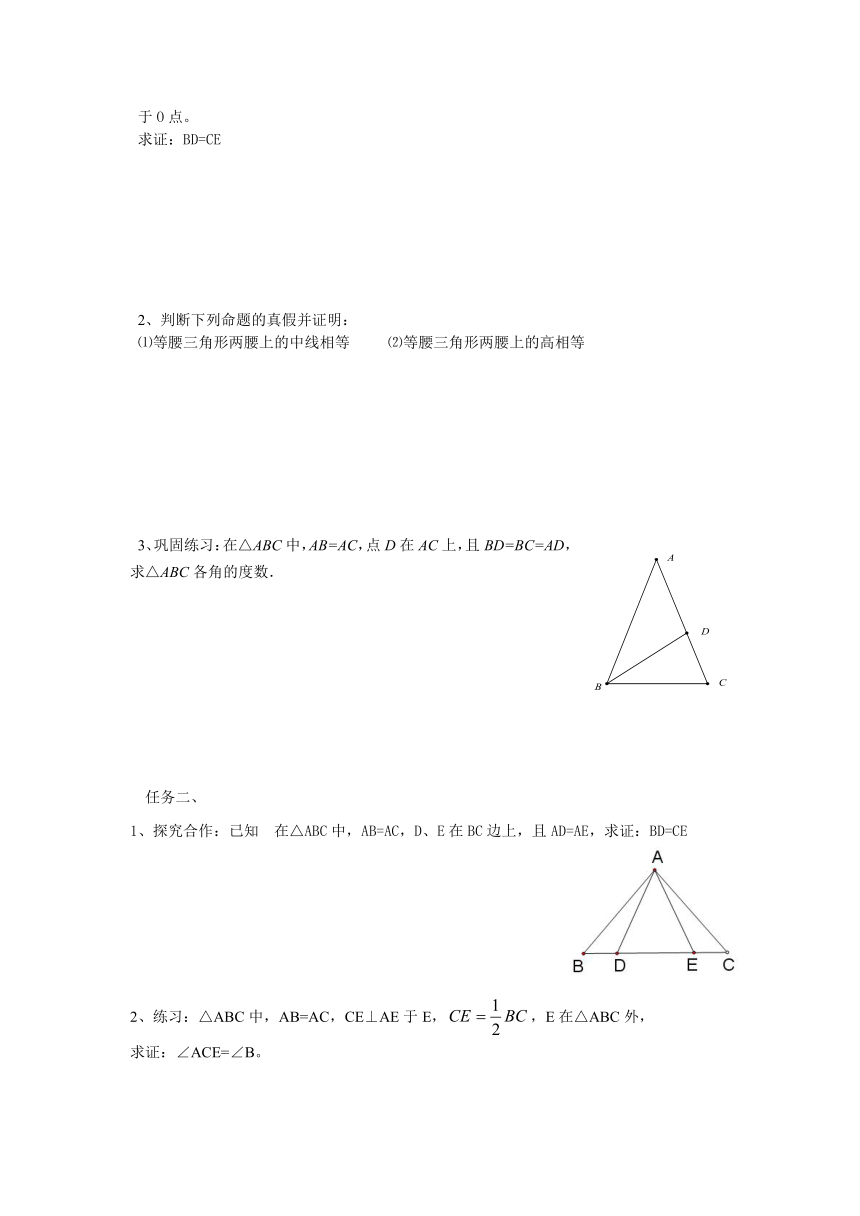
△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且相交于O点。
求证:BD=CE
2、判断下列命题的真假并证明:
⑴等腰三角形两腰上的中线相等 ⑵等腰三角形两腰上的高相等
3、巩固练习:在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,
求△ABC各角的度数.
任务二、
1、探究合作:已知 在△ABC中,AB=AC,D、E在BC边上,且AD=AE,求证:BD=CE
2、练习:△ABC中,AB=AC,CE⊥AE于E,,E在△ABC外,
求证:∠ACE=∠B。
课堂检测:
1、等腰三角形中,若底角是65°,则顶角的度数是 。
2、等腰三角形的一个角是70°,则其它两角的度数为 。
3、等腰三角形的周长是10cm,一边长是3cm,则其它两边长分别是 。
4、等腰三角形一腰上的高与另一腰的夹角是20,则等腰三角形的底角是 。
5、等腰三角形的两边长分别为25cm和13cm,则它的周长是( )
A.63cm B.51cm C.63cm和51cm D.以上都不正确
8、已知:如图,D、E分别是AB、AC上的点,AC=BC=BD,
AD=AE,DE=CE,求∠B的度数。
10、已知:如图,Rt△ABC中, ∠BAC=90,AB=AC,D是 BC的中点,且AE=BF。
求证(1) DE=DF
(2) △DEF为等腰直角三角形。
等腰三角形导学案第三课时
一、教学目标:
理解等边三角形的性质和判定定理
熟练应用等边三角形的性质和判定解决实际问题
理解、应用直角三角形的边角性质
教学过程
任务一
1、自主学习:⑴一个等腰三角形满足什么条件便成为等边三角形?
⑵你认为有一个角等于600,的等腰三角形是等边三角形吗?你能证明你的结论吗?把你的证明思路与组员交流。
等边三角形的判定定理1: 。
∵ ∴
等边三角形的判定定理2: 。
∵ ∴
等边三角形的判性质定理: 。
∵ ∴
2、△ABC是等边三角形,DE∥BC,
求证:△ADE是等边三角形
△ABC是等边三角形,过它的三个顶点分别作对边的平行线,
得到一个新的三角形△DEF,则△DEF是等边三角形吗?为什么?
任务二
1、合作探究:用两个含300角的三角尺,你能拼成一个怎样的三角形?能拼成一个等边三角形吗?你是如何拼的?观察三角尺,在一个直角三角形中,300角所对的直角边与斜边有什么关系?你能证明你的结论吗?
结论:在直角三角形中,如果有一个角等于300,那么 ,
∵ ∴
2、巩固练习:如图,等腰三角形的底角为150,腰长为2a,求腰上的高
房梁的一部分如图,其中BC⊥AC,A=300,AB=7.4cm,点D是AB的中点,DE⊥AC,
求BC,DE的长
课堂检测:
已知:如图,在ABC中,C=90,AB的垂直平分线交AC于D,垂足为E,若A=30,DE=2,求DBC的度数和CD的长。
2、如图,AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点,
(1)求证:AF垂直于CD.(2)在你连接BE后,还能得出什么新的结论 请写出三个.(不要求证明)
等腰三角形第四课时
一、教学目标
知识与技能:了解反证法的证明步骤,体会反证法证明问题的思想,并能够运用反证法来证明一些问题。
过程与方法:理解并体会反证法的思想内涵。
二、学习重、难点
重点:反证法的证明步骤。难点:运用反证法证题。
三、学习过程
(一)、情境导入
问题1 小龙和小明看过电影后走出电影院,小明扫视周围后不假思索的唠叨:“下了雨,天还这么热。”
小明很诧异,问:“哪里下了雨?”“你没看到马路快车道上全是湿漉漉的吗?”
“没有下雨,这是洒水车洒的。”
小明有理有据的回答:“如果下雨的话,不仅快车道上湿,慢车道和人行道上也要湿。你看,除了快车道外,其它地方都不湿,所以肯定刚才没下雨,”
小龙点点头笑道:“不错,是没有下雨,怪不得天这么闷热。”
思考讨论:
小龙为什么会赞同小明的分析?小明在分析的过程中体现了一种什么数学方法呢?
问题2 我们知道,命题“在直角三角形ABC中,AB=c BC=a CA=b 且∠C=90°那么a2+b2=c2”是真命题。那么请同学们思考讨论:“在三角形ABC中,AB=c BC=a CA=b 且∠C≠90°,那么a2+b2≠c2”是真命题吗?如果是请说明理由。
任务一:自主学习课本P16想一想,各小组根据上面的问题1与问题2的分析交流总结以下问题:
反证法的定义: 。
反证法的步骤:(1)先假设 。(2)然后通过 ,推出与 、 、 或 ,说明假设不成立,从而得到原结论正确。
独立完成小组交流:
任务二、探索交流 ,说出下面的反面的假设
一个三角形至多有一个直角
在一个三角形中,至少有一个角小于或等于600
在一个三角形中,如果两边不相等,那么这两条边所对的角也不相等
任务三、探究提高
例题:求证:在同一平面内,如果一条直线和两条平行线中的一条相交,那么和另一条也相交。
(几何证明题的步骤忘了吗?“一画二写三证”)
已知(题设):_________________________________
求证(结论):__________________________________.
证明:(反证法)
①假设___________ ___________________
②则___________ __________,
这与____________________________________________矛盾。
③所以____________________不成立。
④即求证的命题成立。
课堂练习:用反证法证明:一个三角形至多有一个角是直角
已知(题设):_________________________________
求证(结论):__________________________________.
证明:
假设___________________________,不妨设________ ______。
则____________ _________,
这与____________________________________________矛盾。
所以____________________不成立。
所以
巩固练习:
求证:在一个三角形中,至少有一个内角小于或等于60°
2、试证明:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
四、达标检测
试用反证法证明下列结论
求证在一个三角形中,如果两个角不等,那么他们所对的边也不等 。
五、在本节课中,你的收获是:
还有哪些问题没有解决?
A
B
C
D
C
O
E
A
B
D
A
E
D
C
B
A
B
C
D
B
A
D
C
A
B
C
D
E
二写
三证
一画
教学目标:1、理解等腰三角形的性质和判定定理
2、利用定理证明解决实际问题
任务一:
自主学习:(独立完成,组内交流,课堂展示)
⑵如图1,已知△ABC中,AB=AC,AD是底边上的中线.
(1) 求证:∠B=∠C;(2) AD平分∠A,AD⊥BC .
图1
归纳:等腰三角形的性质有:
①性质1:等腰三角形的两底角 (简单叙述为: )
∵ ∴
②性质2:等腰三角形的 互相重合
∵ ∴
∵ ∴
∵ ∴
课堂练习:
①、等腰三角形一个底角为70°,它的顶角为______.
②、等腰三角形一个角为70°,它的另外两个角为 。
③如图3,在△ABC 中AB=AD=DC,∠BAD=26°,
求∠B和∠C度数。
图3
④如图4,∠BAC=1000,AD⊥BC,垂足为点D,AB=AC,
求:∠B, ∠1
图4
任务二
1、自主学习:
如图:△ABC中,∠B=∠C,求证;AB=AC
归纳:等腰三角形判定定理: (简单叙述为: )
∵ ∴
思考:要证明△ABC是等腰三角形,你都有哪些方法?
巩固练习:
如图,已知:△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且相交于O点。
⑴ 试说明△OBC是等腰三角形;
⑵ 连接OA,试判断直线OA与线段BC的关系?并说明理由。
课堂检测:
1、等腰三角形有两条边长为4cm和9cm,则该三角形的周长是( )
A.17cm B.22cm C.17cm或22cm D.18cm
2、等腰三角形的顶角是80°,则一腰上的高与底边的夹角是( )
A.40° B.50° C.60° D.30°
3.如图,已知∠1=∠2=∠3,∠B=∠C则图中相等的线段有( )
A.2对 B.3对 C.4对 D.5对
4、如图所示,,点是的交点,点是的中点.试判断和的位置关系,并给出证明.
等腰三角形导学案第二课时
知识回顾:
1.如图:△ABC中,⑴若AB=AC,则___ ____;
⑵若AB=AC, ∠BAD=∠CAD,则 ____ _ ___,____ _____;
若AB=AC, BD=CD,则___ __,__ ____;
若AB=AC, AD⊥BC,则__ ___,__ ____。
(3)△ABC中,如果∠B=∠C,则___ ____
任务一:
1、自主学习:
△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且相交于O点。
求证:BD=CE
2、判断下列命题的真假并证明:
⑴等腰三角形两腰上的中线相等 ⑵等腰三角形两腰上的高相等
3、巩固练习:在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,
求△ABC各角的度数.
任务二、
1、探究合作:已知 在△ABC中,AB=AC,D、E在BC边上,且AD=AE,求证:BD=CE
2、练习:△ABC中,AB=AC,CE⊥AE于E,,E在△ABC外,
求证:∠ACE=∠B。
课堂检测:
1、等腰三角形中,若底角是65°,则顶角的度数是 。
2、等腰三角形的一个角是70°,则其它两角的度数为 。
3、等腰三角形的周长是10cm,一边长是3cm,则其它两边长分别是 。
4、等腰三角形一腰上的高与另一腰的夹角是20,则等腰三角形的底角是 。
5、等腰三角形的两边长分别为25cm和13cm,则它的周长是( )
A.63cm B.51cm C.63cm和51cm D.以上都不正确
8、已知:如图,D、E分别是AB、AC上的点,AC=BC=BD,
AD=AE,DE=CE,求∠B的度数。
10、已知:如图,Rt△ABC中, ∠BAC=90,AB=AC,D是 BC的中点,且AE=BF。
求证(1) DE=DF
(2) △DEF为等腰直角三角形。
等腰三角形导学案第三课时
一、教学目标:
理解等边三角形的性质和判定定理
熟练应用等边三角形的性质和判定解决实际问题
理解、应用直角三角形的边角性质
教学过程
任务一
1、自主学习:⑴一个等腰三角形满足什么条件便成为等边三角形?
⑵你认为有一个角等于600,的等腰三角形是等边三角形吗?你能证明你的结论吗?把你的证明思路与组员交流。
等边三角形的判定定理1: 。
∵ ∴
等边三角形的判定定理2: 。
∵ ∴
等边三角形的判性质定理: 。
∵ ∴
2、△ABC是等边三角形,DE∥BC,
求证:△ADE是等边三角形
△ABC是等边三角形,过它的三个顶点分别作对边的平行线,
得到一个新的三角形△DEF,则△DEF是等边三角形吗?为什么?
任务二
1、合作探究:用两个含300角的三角尺,你能拼成一个怎样的三角形?能拼成一个等边三角形吗?你是如何拼的?观察三角尺,在一个直角三角形中,300角所对的直角边与斜边有什么关系?你能证明你的结论吗?
结论:在直角三角形中,如果有一个角等于300,那么 ,
∵ ∴
2、巩固练习:如图,等腰三角形的底角为150,腰长为2a,求腰上的高
房梁的一部分如图,其中BC⊥AC,A=300,AB=7.4cm,点D是AB的中点,DE⊥AC,
求BC,DE的长
课堂检测:
已知:如图,在ABC中,C=90,AB的垂直平分线交AC于D,垂足为E,若A=30,DE=2,求DBC的度数和CD的长。
2、如图,AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点,
(1)求证:AF垂直于CD.(2)在你连接BE后,还能得出什么新的结论 请写出三个.(不要求证明)
等腰三角形第四课时
一、教学目标
知识与技能:了解反证法的证明步骤,体会反证法证明问题的思想,并能够运用反证法来证明一些问题。
过程与方法:理解并体会反证法的思想内涵。
二、学习重、难点
重点:反证法的证明步骤。难点:运用反证法证题。
三、学习过程
(一)、情境导入
问题1 小龙和小明看过电影后走出电影院,小明扫视周围后不假思索的唠叨:“下了雨,天还这么热。”
小明很诧异,问:“哪里下了雨?”“你没看到马路快车道上全是湿漉漉的吗?”
“没有下雨,这是洒水车洒的。”
小明有理有据的回答:“如果下雨的话,不仅快车道上湿,慢车道和人行道上也要湿。你看,除了快车道外,其它地方都不湿,所以肯定刚才没下雨,”
小龙点点头笑道:“不错,是没有下雨,怪不得天这么闷热。”
思考讨论:
小龙为什么会赞同小明的分析?小明在分析的过程中体现了一种什么数学方法呢?
问题2 我们知道,命题“在直角三角形ABC中,AB=c BC=a CA=b 且∠C=90°那么a2+b2=c2”是真命题。那么请同学们思考讨论:“在三角形ABC中,AB=c BC=a CA=b 且∠C≠90°,那么a2+b2≠c2”是真命题吗?如果是请说明理由。
任务一:自主学习课本P16想一想,各小组根据上面的问题1与问题2的分析交流总结以下问题:
反证法的定义: 。
反证法的步骤:(1)先假设 。(2)然后通过 ,推出与 、 、 或 ,说明假设不成立,从而得到原结论正确。
独立完成小组交流:
任务二、探索交流 ,说出下面的反面的假设
一个三角形至多有一个直角
在一个三角形中,至少有一个角小于或等于600
在一个三角形中,如果两边不相等,那么这两条边所对的角也不相等
任务三、探究提高
例题:求证:在同一平面内,如果一条直线和两条平行线中的一条相交,那么和另一条也相交。
(几何证明题的步骤忘了吗?“一画二写三证”)
已知(题设):_________________________________
求证(结论):__________________________________.
证明:(反证法)
①假设___________ ___________________
②则___________ __________,
这与____________________________________________矛盾。
③所以____________________不成立。
④即求证的命题成立。
课堂练习:用反证法证明:一个三角形至多有一个角是直角
已知(题设):_________________________________
求证(结论):__________________________________.
证明:
假设___________________________,不妨设________ ______。
则____________ _________,
这与____________________________________________矛盾。
所以____________________不成立。
所以
巩固练习:
求证:在一个三角形中,至少有一个内角小于或等于60°
2、试证明:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
四、达标检测
试用反证法证明下列结论
求证在一个三角形中,如果两个角不等,那么他们所对的边也不等 。
五、在本节课中,你的收获是:
还有哪些问题没有解决?
A
B
C
D
C
O
E
A
B
D
A
E
D
C
B
A
B
C
D
B
A
D
C
A
B
C
D
E
二写
三证
一画
