北师大版数学七年级下第二章 平行线与相交线 学案
文档属性
| 名称 | 北师大版数学七年级下第二章 平行线与相交线 学案 |  | |
| 格式 | zip | ||
| 文件大小 | 322.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-11 17:05:56 | ||
图片预览


文档简介
第二章 平行线与相交线
2.1 余角与补角
【学习目标】
了解补角,余角和对顶角,知道等角的余角相等,等角的补角相等,对顶角相等,并能解决一些实际问题.
【预习设计】
1.已知:∠1=34°,∠1和∠2互为余角,∠1和∠3互为补角,则∠2= ;∠3= .?
2.已知锐角∠1,则∠1的余角可表示成 ;∠1的补角可表示成 . 3.①若∠A+∠B=90°,∠C+∠B=90°,则∠A ∠C(填“>”或“=”或“<”),
理由是 .
②若∠1+∠3=180°,∠2+∠4=180°,且∠1=∠2,则∠3 ∠4(填“>”或“=”或“<”),理由是 .?4.如图,直线AB和CD相交于点O,∠DOE是直角,若∠1=30°,则∠2= ,∠3= ,∠4= .?
【学习探究】
一、学前准备:
1.余角、补角的定义。
①互为余角:
②互为补角:
③邻补角:
2.余角、补角的性质
的余角相等; 的补角相等。
3.对顶角
①特征:
②性质:
特别注意
1.互为余角,互为补角都是指两个角的数量关系,与位置无关
2.对顶角出现的前提条件是两直线相交。
二 师生互动
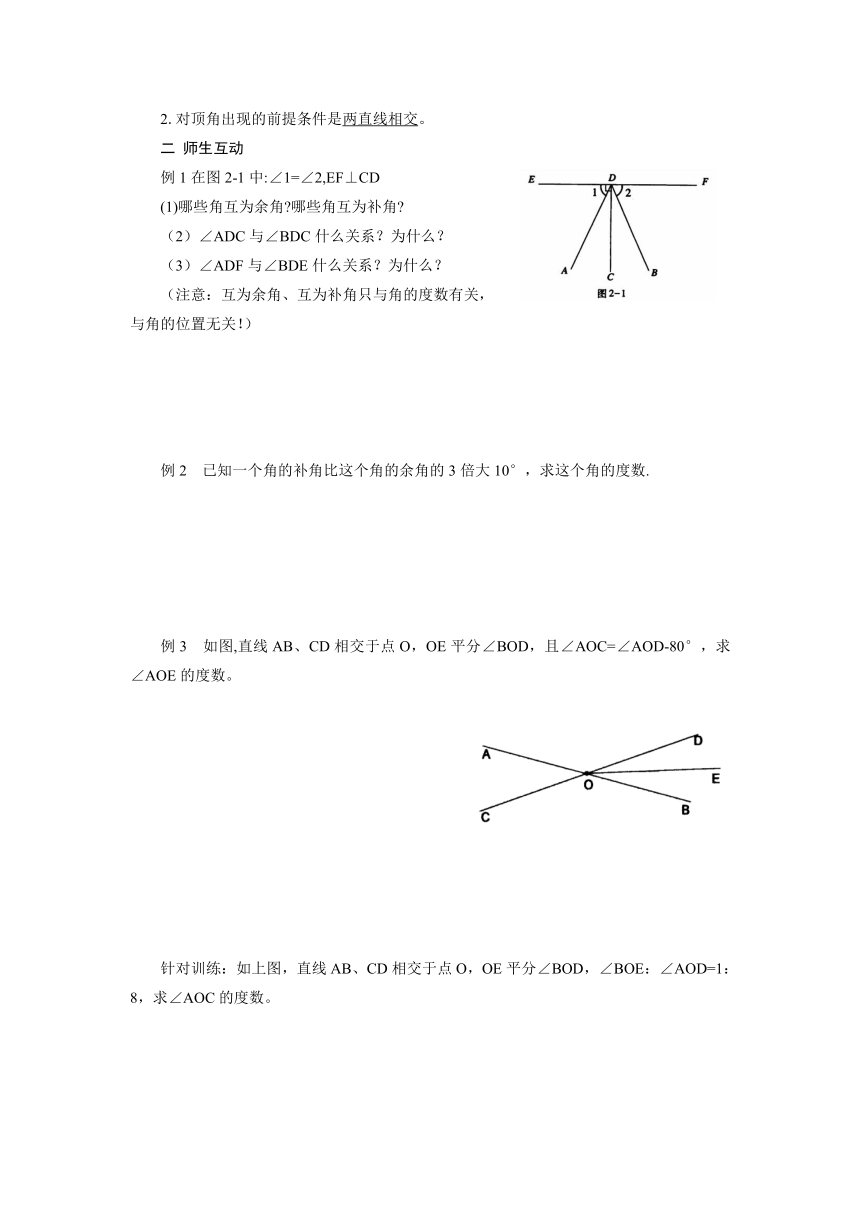
例1在图2-1中:∠1=∠2,EF⊥CD
(1)哪些角互为余角 哪些角互为补角
(2)∠ADC与∠BDC什么关系?为什么?
(3)∠ADF与∠BDE什么关系?为什么?
(注意:互为余角、互为补角只与角的度数有关,
与角的位置无关!)
例2 已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.
例3 如图,直线AB、CD相交于点O,OE平分∠BOD,且∠AOC=∠AOD-80°,求∠AOE的度数。
针对训练:如上图,直线AB、CD相交于点O,OE平分∠BOD,∠BOE:∠AOD=1:8,求∠AOC的度数。
三、训练测评
1.判断题.
(1)有公共点,且相等的角是对顶角。 ( )
(2)一个角的补角必大于这个角 ( )
(3) 互余的两个角一定都是锐角。 ( )
(4) 若∠1+∠2+∠3=180°,则它们互为补角。 ( )
(5) 两条直线相交,构成两对对顶角 ( )
2.如图,直线AB、CD、EF都过点O,且∠AOC=25°,∠COE=45 °,则∠EOB=_______,∠BOC=_______,∠DOF=___________,∠FOA=__________。
3. 已知一个角的余角比这个角的补角的大26°,求这个角的度数。
4.如图,直线AB、CD相交于点O,∠BOD=40°,OA平分∠EOC,求∠BOE的度数。
四、拓展延伸
1.P62问题解决.
2.P61数学理解1.
3.(趣味数学)观察下图中的图形,寻找对顶角(不含平角)
(1)图①中有 对对顶角;图②中有 对对顶角;图③中有 对对顶角;
(2)若有n条直线相交于一点,则可形成 对对顶角;若有180条直线相交于一点,则可形成 对对顶角。
2.2 探索直线平行的条件(1)
【学习目标】
1.能正确判断同位角。
2.能利用直线平行的条件判断两直线平行。
【预习设计】
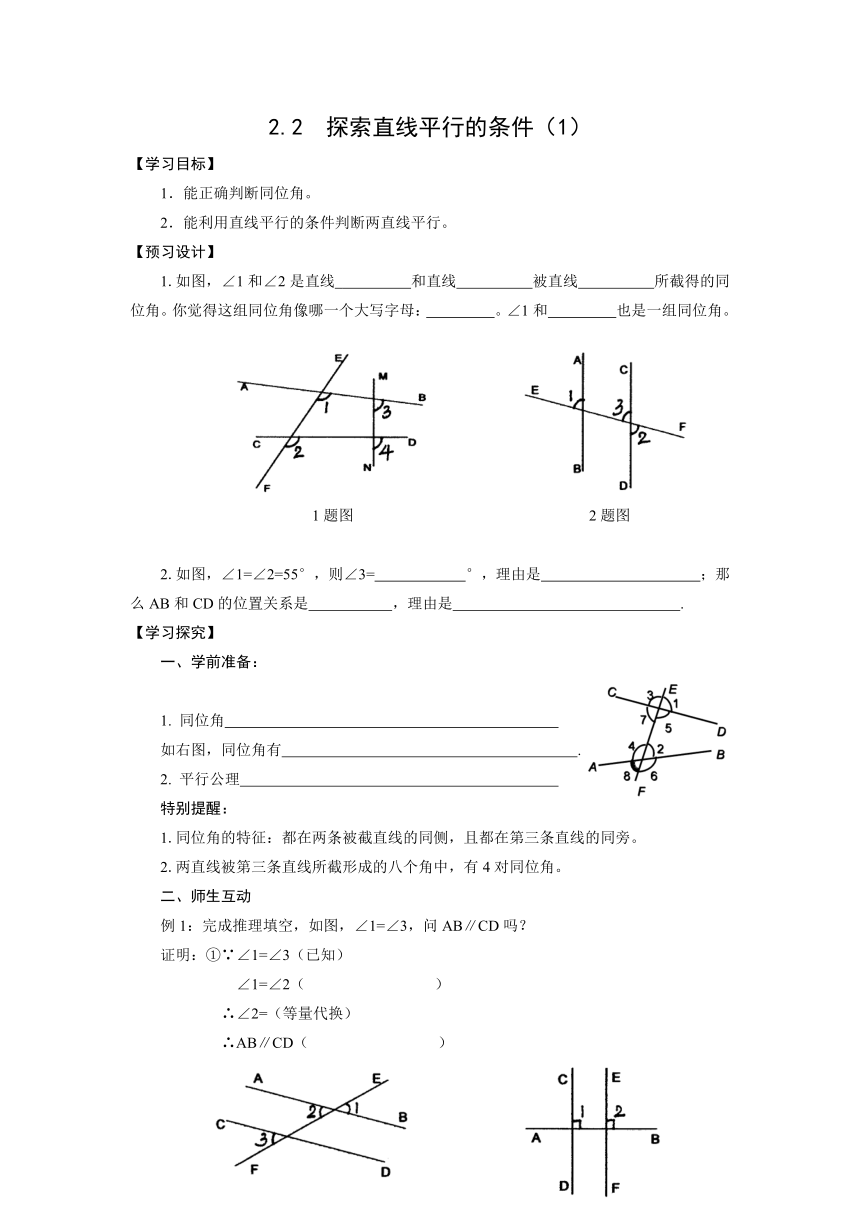
1.如图,∠1和∠2是直线 和直线 被直线 所截得的同位角。你觉得这组同位角像哪一个大写字母: 。∠1和 也是一组同位角。
1题图 2题图
2.如图,∠1=∠2=55°,则∠3= °,理由是 ;那么AB和CD的位置关系是 ,理由是 .?
【学习探究】
一、学前准备:
1. 同位角
如右图,同位角有 .?
2. 平行公理
特别提醒:
1.同位角的特征:都在两条被截直线的同侧,且都在第三条直线的同旁。
2.两直线被第三条直线所截形成的八个角中,有4对同位角。
二、师生互动
例1:完成推理填空,如图,∠1=∠3,问AB∥CD吗?
证明:①∵∠1=∠3(已知)
∠1=∠2( )
∴∠2=(等量代换)
∴AB∥CD( )
①题图 ②题图
②如图,AB⊥CD,AB⊥EF,问CD∥EF吗?
证明:∵AB⊥CD,AB⊥EF(已知)
∴∠1= = °(垂直的定义)
∴ ∥ ( )
请你用一句精练的话总结上述规律:?
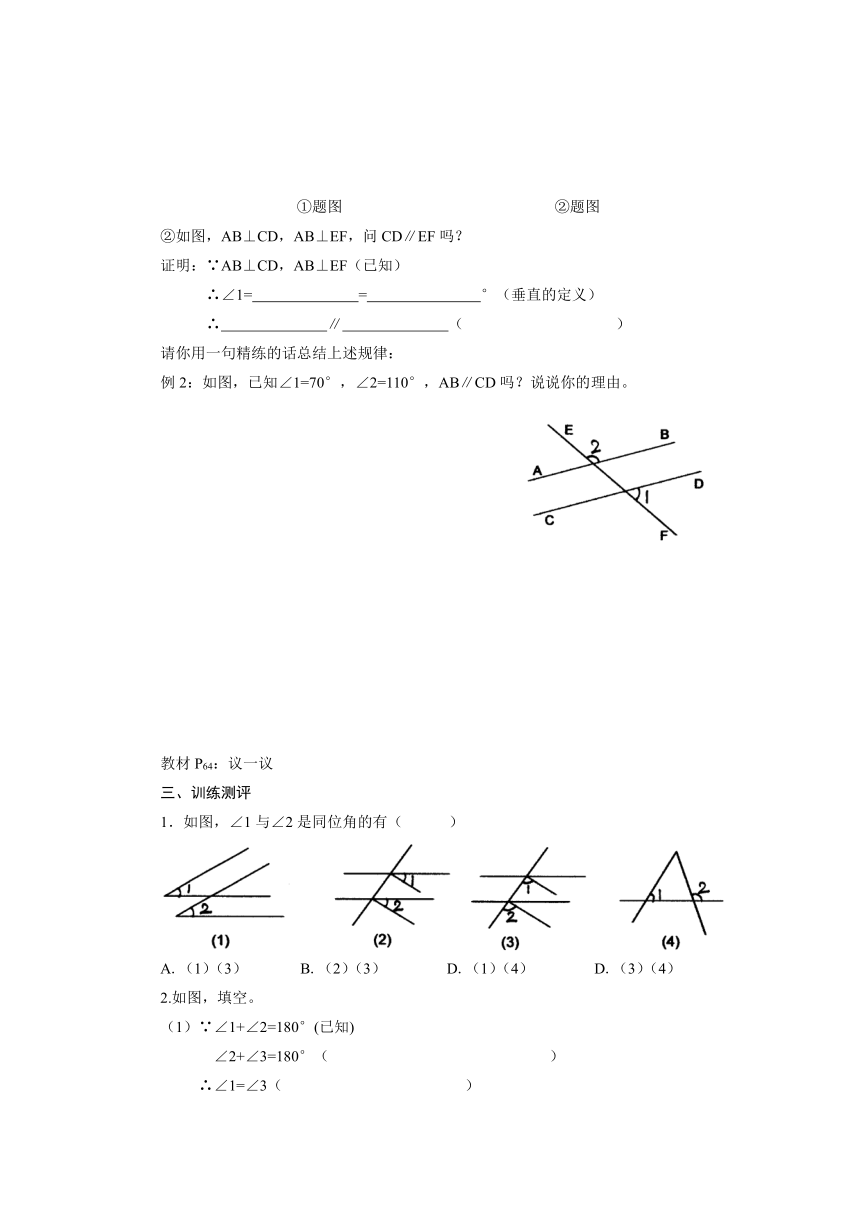
例2:如图,已知∠1=70°,∠2=110°,AB∥CD吗?说说你的理由。
教材P64:议一议
三、训练测评
1.如图,∠1与∠2是同位角的有( )
A.(1)(3) B.(2)(3) D.(1)(4) D.(3)(4)
2.如图,填空。
(1)∵∠1+∠2=180°(已知)
∠2+∠3=180°( )
∴∠1=∠3( )
∴AB∥ ( )
(2) ∵∠7=∠4(已知)
又∵∠7=∠8( )
∴∠8=∠4( )
∴ ∥ ( )
3.如图,已知∠ABC=30°, ∠ADC=60°,DE为∠ADC的平分线,你能判断哪两条直线平行,并说明理由。
四、拓展延伸
如图,AB⊥l1于D,BC交l2于E,∠1与∠2满足什么关系时,l1∥l2 请说明理由。
【课后反思】
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的 ,在截线的 形如字母 。(或倒置,反置)
2.2 探索直线平行的条件(2)
【学习目标】
1.能正确判断同位角,内错角,同旁内角。
2.能利用直线平行的条件判断两直线平行。
【预习设计】
1.如图,∠1与是 同位角,形如字母
∠1与是 内错角,你觉得像字母 ?
∠1与是 同旁内角,你觉得像字母
? 1题图 2题图
2.如图:①∠1=50°,∠2= °时,AB∥CD?
②∠1=70°,∠3= °时,AB∥CD?
【学习探究】
一、学前准备:
1.内错角
2.同旁内角
3.两条直线平行的判定方法
①
②
③
二、师生互动
例1、观察右图并填空:
(1)∠1与 是同位角;∠5 与 是同旁内角;∠5 与 是内错角;
(2)找出右图中的同位角,内错角和同旁内角。
例2:如图,①如果∠1=∠D,那么 ∥ ,
理由是 .?
②如果∠1=∠B,那么 ∥ ,
理由是 .?
③如果∠A+∠B=180°,那么 ∥ ,
理由是 ?
④如果∠A+∠D=180°,那么 ∥ ,理由是
练习P68随堂练习。
三、训练测评
1.如右图,已知:∠2=∠3,∠1+∠3=180°,求证:EF∥GH.。
证明:∵∠2=∠3 (已知)
∠1+∠3=180°( )
∴∠1+∠2=180°( )
∴ ( )
2.已知,如右图,∠1=∠ABC=∠ADC,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°。
(1)∵∠1=∠ABC(已知)
∴AD∥ ( )
(2) ∵∠3=∠5(已知)
∴AB∥ ( )
(3)∵∠2=∠4(已知)
∴ ∥ ( )
(4)∵∠1=∠ADC(已知)
∴ ∥ ( )
(5)∵∠ABC+∠BCD=180°(已知)
∴ ∥ ( )
3.如图,AB⊥AD,AD⊥CD, ∠1=∠2,说出AE和DF的关系,并说明理由。
变式练习:如图,∠1=∠2,请你添加一个条件 使AE∥DF并给予证明(除AB⊥AD,AD⊥CD).
四.拓展延伸
如图,已知∠1=∠2,∠DAB=∠DCB,AE平分∠DAB且交BC于E,CF平分∠DCB且交AD于F。求证: AD∥BC。
【课后反思】
??形如字母
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的 ,在截线的 . 形如字母 。(或倒置,反置)
内错角 在两条被截直线之间,在截线的 . 形如字母 。(或反置)
同旁内角 在两条被截直线的 ,在截线的 . 形如字母 。
2.3 平行线的特征
【学习目标】
1. 认识平行线的特征。
2. 运用平行线的特征进行简单的推理运算。
【预习设计】
如图,直线AB、CD相交于E,AB∥DF,若∠AEC=100°,则∠D= .?
1题图 2题图
2.如图,AB∥CD,OB平分∠EOD,∠1=30°,则∠2= .?
【学习探究】
一、学前准备:
两条平行直线被第三条直线直线所截,
判定定理 性质定理
已知 结论 已知 结论
特别注意
平行线的判定是:已知角的关系,结论是两直线平行。
平行线的性质是:已知两直线平行,结论是角的关系。
角的关系 平行线
二、师生互动
例1.如图,已知AB//CD,∠3:∠2=3:1,求∠1的度数.
例2:如图,已知AC∥DE,∠1=∠2,AB∥CD吗?说明理由。
例3:如图,已知AB⊥AD,AB⊥CE,FG⊥BD,∠1=∠2,求证AC⊥BD?
练一练P73知识技能1,2。
三、训练测评
1.如图,AB∥CD,AD∥BC,∠A是∠B的2倍,则∠A= °,∠1= °
? 1题图 2题图
2.如图,AB∥CD∥EF,如果∠A=150°,∠C=130°,则∠AEC= .? 3.如图,AB∥CD,∠A=30°,∠C=50°,∠AEC= .
3题图 4题图
4.如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论(1)AB//CD;(2)AD//BC;(3)∠B=∠D;(4)∠D=∠ACB。其中正确的有( )
A、1个 B、2个
C、3个 D、4个
5.如图,要得到DE ∥BC,则需要满足的条件是( )
A.∠2+∠5=180° B.∠3+∠5=180°
C.∠2=∠4 D.∠1=∠2
6.如果两个角的一对边在同一直线上,另一对边互相平行,则这两个角( )
A、相等 B、互补
C、相等或互余 D、相等或互补
7.下列说法中,错误的是( )
A.两直线平行,同位角的平分线互相平行
B.两直线平行,内错角的平分线互相平行
C.两直线平行,同旁内角的平分线互相平行
D.两直线平行,同旁内角的平分线互相垂直
8.如右图,已知∠1=60°,∠2=60°,∠3=78°,求∠4.
四、拓展延伸.
1.如图,AB∥CD,猜想∠BED与∠B、∠D的大小关系,并给予证明。
2.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=75°,求∠BFD度数。
2.4 用尺规作线段和角(1)
【学习目标】
1.会用尺规作一条线段等于已知线段。
2.了解尺规作图的简单应用。
【学习探究】
一、学前准备
1.尺规作图:在几何中,限定用直尺和圆规来画图,称为尺规作图。
注意:直尺是指没有刻度的尺子。
2.尺规作图的解解的基本要求与格式
格式:已知……
求作……
作法……(作法的每一步必须有依据)
3.一些常见的作图语句
射线与直线:画射线××;过点×作直线××;或作直线××,或作射线××?
线段:连接两点×、×;或连接××?
截线段:在××上截取××=××?
延长线:延长××到点×,或延长××到点×,使××=××?
二、师生互动
例题1:P74做一做
例题2:已知线段a,b,你能作出线段c ,使c=2a-b吗?
三、训练测评
1.P75随堂练习
2.已知线段a和b,
(1)求作:线段AC,使AC=a+b.
(2)求作:线段AD,使AD=b-a
3.已知线段a和b(上题图中的线段a和b),
(1)求作:线段AC,使AC=2a+3b.
(2)求作:线段AD,使AD=3b-2a
四、拓展延伸
P78【读一读】
【课后反思】
2.4 用尺规作线段和角(2)
【学习目标】
1. 会用尺规作一个角等于已知角.
2. 了解尺规作图的简单应用。
【学习探究】
一、学前准备:
用尺规作角
基本作图:作一个角等于已知角
作用:作三角形的角和作平行线等。
常见作图语言:(1)作∠×××=∠×××?
(2)作××(射线)平分∠×××?
(3)过点×作××⊥××,垂足为点×?
二、师生互动
例1.完成图2-14的作图
例2.P76做一做
三、训练测评
1.求作∠A′O′B′, 使∠A′O′B′等于已知角∠AOB(如图所示)
(1) 作射线O′A ′;
(2) 以点 为圆心,以 为半径画弧交OA于点C交OB于点D;
(3) 以点 为圆心,以 为半径画弧交O′A ′于点C ′;
(4) 以点 为圆心,以 为半径画弧,交前面的弧于点D ′;
(5) 过点 作射线O′B ′,则 就是所求作的角 。 2.如图所示,已知∠α,∠β(∠α﹥∠β).(不写作法,保留作图痕迹)
(1) 求作∠AOB,使∠AOB=∠α+∠β;
(2)求作∠COD, 使∠COD=∠α﹣∠β.
3.已知线段a,b,求作△ABC,使其一个内角为∠α,且∠α的两边分别等于a,b.(不写作法,保留作图痕迹)
4.请你按照要求作图(利用上题的∠α和线段a,b),利用直尺和圆规作图。(不写作法,保留作图痕迹)
①作∠BAC=∠α; ②在AB上截取AD=a;
③过点D作DE//AC; ④在DE上截取DF=b;
⑤作∠DFG=∠α,交AC于G.你得到的ADFG是一个什么图形?
5.已知∠AOB及两边上的点M、N(如图)请用尺规分别过M、N点作OB、OA的平行线,不写作法,保留作图痕迹。
四、拓展延伸(用尺规作优美的图案)
右图的“雏菊图案”漂亮吗?你想自己画出它来吗?
那就让我们从最初的步骤开始吧
1.以点O为圆心,r 为半径作圆O;
2.以圆O上任意一点为圆心,r 为半径作圆,与圆O交于两点;
3.分别以两个交点为圆心,r 为半径作圆;
4、继续作下去,在适当的区域涂上颜色。
【课后反思】
第二章 平行线与相交线(专题复习)
一、学习目标
1.补角,余角,对顶角,及三线八角等基本概念及性质的考查。
2.学会有关角的计算,及直线平行的性质与判定的应用。
二、本章知识结构
三、专题讲解
(一)例题讲解
例1如图,一个经过改造的台球桌面的示意图,四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球经过多次反射),那么球最后将落入的球袋是( )
A.1号袋 B.2号袋
C.3号袋 D.4号袋
例2.如图, AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数。
例3.已知AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,求∠P的度数。
(二)方法总结:
1、与平行线相关的问题一般都是直线平行的条件和平行线的特征的综合运用,要体现在以下两个方面:
(1)由角定角已知角的关系判定两直线平行特征确定其它角的关系
(2)由线定线已知两线平行特征角的关系判定确定其它直线平行
2、角的有关计算问题,结合平行线的特征、余角、补角、角平分线的定义等知识通过列方程解决。
【课后反思】
判定
====
性质
2.1 余角与补角
【学习目标】
了解补角,余角和对顶角,知道等角的余角相等,等角的补角相等,对顶角相等,并能解决一些实际问题.
【预习设计】
1.已知:∠1=34°,∠1和∠2互为余角,∠1和∠3互为补角,则∠2= ;∠3= .?
2.已知锐角∠1,则∠1的余角可表示成 ;∠1的补角可表示成 . 3.①若∠A+∠B=90°,∠C+∠B=90°,则∠A ∠C(填“>”或“=”或“<”),
理由是 .
②若∠1+∠3=180°,∠2+∠4=180°,且∠1=∠2,则∠3 ∠4(填“>”或“=”或“<”),理由是 .?4.如图,直线AB和CD相交于点O,∠DOE是直角,若∠1=30°,则∠2= ,∠3= ,∠4= .?
【学习探究】
一、学前准备:
1.余角、补角的定义。
①互为余角:
②互为补角:
③邻补角:
2.余角、补角的性质
的余角相等; 的补角相等。
3.对顶角
①特征:
②性质:
特别注意
1.互为余角,互为补角都是指两个角的数量关系,与位置无关
2.对顶角出现的前提条件是两直线相交。
二 师生互动
例1在图2-1中:∠1=∠2,EF⊥CD
(1)哪些角互为余角 哪些角互为补角
(2)∠ADC与∠BDC什么关系?为什么?
(3)∠ADF与∠BDE什么关系?为什么?
(注意:互为余角、互为补角只与角的度数有关,
与角的位置无关!)
例2 已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.
例3 如图,直线AB、CD相交于点O,OE平分∠BOD,且∠AOC=∠AOD-80°,求∠AOE的度数。
针对训练:如上图,直线AB、CD相交于点O,OE平分∠BOD,∠BOE:∠AOD=1:8,求∠AOC的度数。
三、训练测评
1.判断题.
(1)有公共点,且相等的角是对顶角。 ( )
(2)一个角的补角必大于这个角 ( )
(3) 互余的两个角一定都是锐角。 ( )
(4) 若∠1+∠2+∠3=180°,则它们互为补角。 ( )
(5) 两条直线相交,构成两对对顶角 ( )
2.如图,直线AB、CD、EF都过点O,且∠AOC=25°,∠COE=45 °,则∠EOB=_______,∠BOC=_______,∠DOF=___________,∠FOA=__________。
3. 已知一个角的余角比这个角的补角的大26°,求这个角的度数。
4.如图,直线AB、CD相交于点O,∠BOD=40°,OA平分∠EOC,求∠BOE的度数。
四、拓展延伸
1.P62问题解决.
2.P61数学理解1.
3.(趣味数学)观察下图中的图形,寻找对顶角(不含平角)
(1)图①中有 对对顶角;图②中有 对对顶角;图③中有 对对顶角;
(2)若有n条直线相交于一点,则可形成 对对顶角;若有180条直线相交于一点,则可形成 对对顶角。
2.2 探索直线平行的条件(1)
【学习目标】
1.能正确判断同位角。
2.能利用直线平行的条件判断两直线平行。
【预习设计】
1.如图,∠1和∠2是直线 和直线 被直线 所截得的同位角。你觉得这组同位角像哪一个大写字母: 。∠1和 也是一组同位角。
1题图 2题图
2.如图,∠1=∠2=55°,则∠3= °,理由是 ;那么AB和CD的位置关系是 ,理由是 .?
【学习探究】
一、学前准备:
1. 同位角
如右图,同位角有 .?
2. 平行公理
特别提醒:
1.同位角的特征:都在两条被截直线的同侧,且都在第三条直线的同旁。
2.两直线被第三条直线所截形成的八个角中,有4对同位角。
二、师生互动
例1:完成推理填空,如图,∠1=∠3,问AB∥CD吗?
证明:①∵∠1=∠3(已知)
∠1=∠2( )
∴∠2=(等量代换)
∴AB∥CD( )
①题图 ②题图
②如图,AB⊥CD,AB⊥EF,问CD∥EF吗?
证明:∵AB⊥CD,AB⊥EF(已知)
∴∠1= = °(垂直的定义)
∴ ∥ ( )
请你用一句精练的话总结上述规律:?
例2:如图,已知∠1=70°,∠2=110°,AB∥CD吗?说说你的理由。
教材P64:议一议
三、训练测评
1.如图,∠1与∠2是同位角的有( )
A.(1)(3) B.(2)(3) D.(1)(4) D.(3)(4)
2.如图,填空。
(1)∵∠1+∠2=180°(已知)
∠2+∠3=180°( )
∴∠1=∠3( )
∴AB∥ ( )
(2) ∵∠7=∠4(已知)
又∵∠7=∠8( )
∴∠8=∠4( )
∴ ∥ ( )
3.如图,已知∠ABC=30°, ∠ADC=60°,DE为∠ADC的平分线,你能判断哪两条直线平行,并说明理由。
四、拓展延伸
如图,AB⊥l1于D,BC交l2于E,∠1与∠2满足什么关系时,l1∥l2 请说明理由。
【课后反思】
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的 ,在截线的 形如字母 。(或倒置,反置)
2.2 探索直线平行的条件(2)
【学习目标】
1.能正确判断同位角,内错角,同旁内角。
2.能利用直线平行的条件判断两直线平行。
【预习设计】
1.如图,∠1与是 同位角,形如字母
∠1与是 内错角,你觉得像字母 ?
∠1与是 同旁内角,你觉得像字母
? 1题图 2题图
2.如图:①∠1=50°,∠2= °时,AB∥CD?
②∠1=70°,∠3= °时,AB∥CD?
【学习探究】
一、学前准备:
1.内错角
2.同旁内角
3.两条直线平行的判定方法
①
②
③
二、师生互动
例1、观察右图并填空:
(1)∠1与 是同位角;∠5 与 是同旁内角;∠5 与 是内错角;
(2)找出右图中的同位角,内错角和同旁内角。
例2:如图,①如果∠1=∠D,那么 ∥ ,
理由是 .?
②如果∠1=∠B,那么 ∥ ,
理由是 .?
③如果∠A+∠B=180°,那么 ∥ ,
理由是 ?
④如果∠A+∠D=180°,那么 ∥ ,理由是
练习P68随堂练习。
三、训练测评
1.如右图,已知:∠2=∠3,∠1+∠3=180°,求证:EF∥GH.。
证明:∵∠2=∠3 (已知)
∠1+∠3=180°( )
∴∠1+∠2=180°( )
∴ ( )
2.已知,如右图,∠1=∠ABC=∠ADC,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°。
(1)∵∠1=∠ABC(已知)
∴AD∥ ( )
(2) ∵∠3=∠5(已知)
∴AB∥ ( )
(3)∵∠2=∠4(已知)
∴ ∥ ( )
(4)∵∠1=∠ADC(已知)
∴ ∥ ( )
(5)∵∠ABC+∠BCD=180°(已知)
∴ ∥ ( )
3.如图,AB⊥AD,AD⊥CD, ∠1=∠2,说出AE和DF的关系,并说明理由。
变式练习:如图,∠1=∠2,请你添加一个条件 使AE∥DF并给予证明(除AB⊥AD,AD⊥CD).
四.拓展延伸
如图,已知∠1=∠2,∠DAB=∠DCB,AE平分∠DAB且交BC于E,CF平分∠DCB且交AD于F。求证: AD∥BC。
【课后反思】
??形如字母
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的 ,在截线的 . 形如字母 。(或倒置,反置)
内错角 在两条被截直线之间,在截线的 . 形如字母 。(或反置)
同旁内角 在两条被截直线的 ,在截线的 . 形如字母 。
2.3 平行线的特征
【学习目标】
1. 认识平行线的特征。
2. 运用平行线的特征进行简单的推理运算。
【预习设计】
如图,直线AB、CD相交于E,AB∥DF,若∠AEC=100°,则∠D= .?
1题图 2题图
2.如图,AB∥CD,OB平分∠EOD,∠1=30°,则∠2= .?
【学习探究】
一、学前准备:
两条平行直线被第三条直线直线所截,
判定定理 性质定理
已知 结论 已知 结论
特别注意
平行线的判定是:已知角的关系,结论是两直线平行。
平行线的性质是:已知两直线平行,结论是角的关系。
角的关系 平行线
二、师生互动
例1.如图,已知AB//CD,∠3:∠2=3:1,求∠1的度数.
例2:如图,已知AC∥DE,∠1=∠2,AB∥CD吗?说明理由。
例3:如图,已知AB⊥AD,AB⊥CE,FG⊥BD,∠1=∠2,求证AC⊥BD?
练一练P73知识技能1,2。
三、训练测评
1.如图,AB∥CD,AD∥BC,∠A是∠B的2倍,则∠A= °,∠1= °
? 1题图 2题图
2.如图,AB∥CD∥EF,如果∠A=150°,∠C=130°,则∠AEC= .? 3.如图,AB∥CD,∠A=30°,∠C=50°,∠AEC= .
3题图 4题图
4.如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论(1)AB//CD;(2)AD//BC;(3)∠B=∠D;(4)∠D=∠ACB。其中正确的有( )
A、1个 B、2个
C、3个 D、4个
5.如图,要得到DE ∥BC,则需要满足的条件是( )
A.∠2+∠5=180° B.∠3+∠5=180°
C.∠2=∠4 D.∠1=∠2
6.如果两个角的一对边在同一直线上,另一对边互相平行,则这两个角( )
A、相等 B、互补
C、相等或互余 D、相等或互补
7.下列说法中,错误的是( )
A.两直线平行,同位角的平分线互相平行
B.两直线平行,内错角的平分线互相平行
C.两直线平行,同旁内角的平分线互相平行
D.两直线平行,同旁内角的平分线互相垂直
8.如右图,已知∠1=60°,∠2=60°,∠3=78°,求∠4.
四、拓展延伸.
1.如图,AB∥CD,猜想∠BED与∠B、∠D的大小关系,并给予证明。
2.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=75°,求∠BFD度数。
2.4 用尺规作线段和角(1)
【学习目标】
1.会用尺规作一条线段等于已知线段。
2.了解尺规作图的简单应用。
【学习探究】
一、学前准备
1.尺规作图:在几何中,限定用直尺和圆规来画图,称为尺规作图。
注意:直尺是指没有刻度的尺子。
2.尺规作图的解解的基本要求与格式
格式:已知……
求作……
作法……(作法的每一步必须有依据)
3.一些常见的作图语句
射线与直线:画射线××;过点×作直线××;或作直线××,或作射线××?
线段:连接两点×、×;或连接××?
截线段:在××上截取××=××?
延长线:延长××到点×,或延长××到点×,使××=××?
二、师生互动
例题1:P74做一做
例题2:已知线段a,b,你能作出线段c ,使c=2a-b吗?
三、训练测评
1.P75随堂练习
2.已知线段a和b,
(1)求作:线段AC,使AC=a+b.
(2)求作:线段AD,使AD=b-a
3.已知线段a和b(上题图中的线段a和b),
(1)求作:线段AC,使AC=2a+3b.
(2)求作:线段AD,使AD=3b-2a
四、拓展延伸
P78【读一读】
【课后反思】
2.4 用尺规作线段和角(2)
【学习目标】
1. 会用尺规作一个角等于已知角.
2. 了解尺规作图的简单应用。
【学习探究】
一、学前准备:
用尺规作角
基本作图:作一个角等于已知角
作用:作三角形的角和作平行线等。
常见作图语言:(1)作∠×××=∠×××?
(2)作××(射线)平分∠×××?
(3)过点×作××⊥××,垂足为点×?
二、师生互动
例1.完成图2-14的作图
例2.P76做一做
三、训练测评
1.求作∠A′O′B′, 使∠A′O′B′等于已知角∠AOB(如图所示)
(1) 作射线O′A ′;
(2) 以点 为圆心,以 为半径画弧交OA于点C交OB于点D;
(3) 以点 为圆心,以 为半径画弧交O′A ′于点C ′;
(4) 以点 为圆心,以 为半径画弧,交前面的弧于点D ′;
(5) 过点 作射线O′B ′,则 就是所求作的角 。 2.如图所示,已知∠α,∠β(∠α﹥∠β).(不写作法,保留作图痕迹)
(1) 求作∠AOB,使∠AOB=∠α+∠β;
(2)求作∠COD, 使∠COD=∠α﹣∠β.
3.已知线段a,b,求作△ABC,使其一个内角为∠α,且∠α的两边分别等于a,b.(不写作法,保留作图痕迹)
4.请你按照要求作图(利用上题的∠α和线段a,b),利用直尺和圆规作图。(不写作法,保留作图痕迹)
①作∠BAC=∠α; ②在AB上截取AD=a;
③过点D作DE//AC; ④在DE上截取DF=b;
⑤作∠DFG=∠α,交AC于G.你得到的ADFG是一个什么图形?
5.已知∠AOB及两边上的点M、N(如图)请用尺规分别过M、N点作OB、OA的平行线,不写作法,保留作图痕迹。
四、拓展延伸(用尺规作优美的图案)
右图的“雏菊图案”漂亮吗?你想自己画出它来吗?
那就让我们从最初的步骤开始吧
1.以点O为圆心,r 为半径作圆O;
2.以圆O上任意一点为圆心,r 为半径作圆,与圆O交于两点;
3.分别以两个交点为圆心,r 为半径作圆;
4、继续作下去,在适当的区域涂上颜色。
【课后反思】
第二章 平行线与相交线(专题复习)
一、学习目标
1.补角,余角,对顶角,及三线八角等基本概念及性质的考查。
2.学会有关角的计算,及直线平行的性质与判定的应用。
二、本章知识结构
三、专题讲解
(一)例题讲解
例1如图,一个经过改造的台球桌面的示意图,四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球经过多次反射),那么球最后将落入的球袋是( )
A.1号袋 B.2号袋
C.3号袋 D.4号袋
例2.如图, AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数。
例3.已知AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,求∠P的度数。
(二)方法总结:
1、与平行线相关的问题一般都是直线平行的条件和平行线的特征的综合运用,要体现在以下两个方面:
(1)由角定角已知角的关系判定两直线平行特征确定其它角的关系
(2)由线定线已知两线平行特征角的关系判定确定其它直线平行
2、角的有关计算问题,结合平行线的特征、余角、补角、角平分线的定义等知识通过列方程解决。
【课后反思】
判定
====
性质
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
