鲁教版(五四制)七年级下册数学 第十章 回顾与思考 课件(共14张ppt)
文档属性
| 名称 | 鲁教版(五四制)七年级下册数学 第十章 回顾与思考 课件(共14张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 107.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 21:06:46 | ||
图片预览



文档简介
专题学习
---全等三角形中常见的辅助线
连线中考:
问题:如图1,四边形ABCD中, AB=AD ,∠BAD=120° ,∠B=∠ADC=90° .E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
(2)如图2,若四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.
提升:如图,AB=AE,AB⊥AE,AD=AC,AD⊥AC,点M为BC的中点,求证:DE=2AM.
知识要点:
判断三角形全等公理有SAS、ASA、AAS、SSS和HL
有些证明题要添加适当的辅助线构造合适的全等三角形,把条件相对集中起来,再进行等量代换,就可以化难为易了。
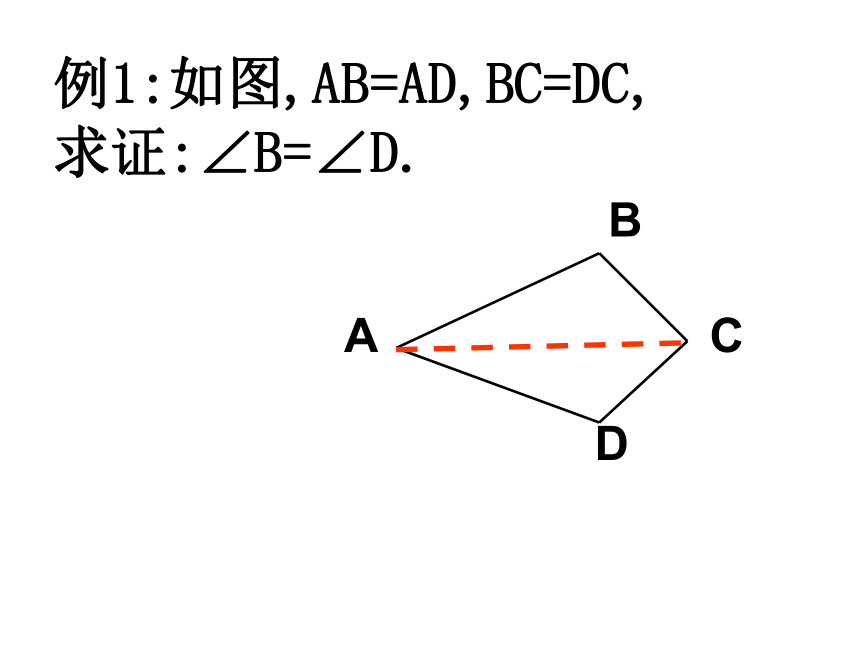
例1:如图,AB=AD,BC=DC,
求证:∠B=∠D.
A
C
B
D
A
C
B
D
N
M
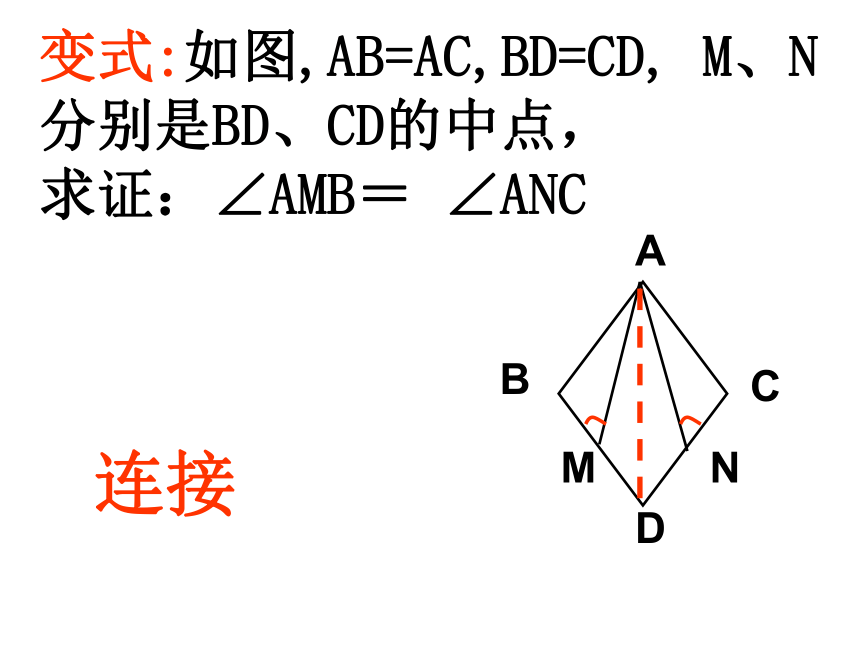
变式:如图,AB=AC,BD=CD, M、N分别是BD、CD的中点,
求证:∠AMB= ∠ANC
连接
A
C
B
D
E
M
练习:如图,AB=AE,BC=ED, ∠B=∠E,AM⊥CD,
求证:点M是CD的中点.
你还能得到哪些结论?
A
C
D
B
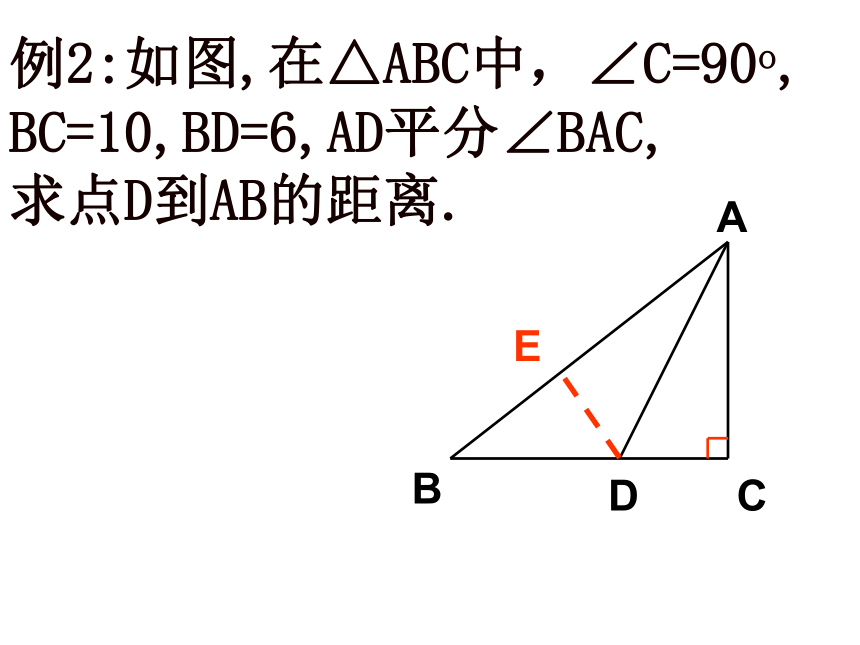
例2:如图,在△ABC中,∠C=90o,
BC=10,BD=6,AD平分∠BAC,
求点D到AB的距离.
E
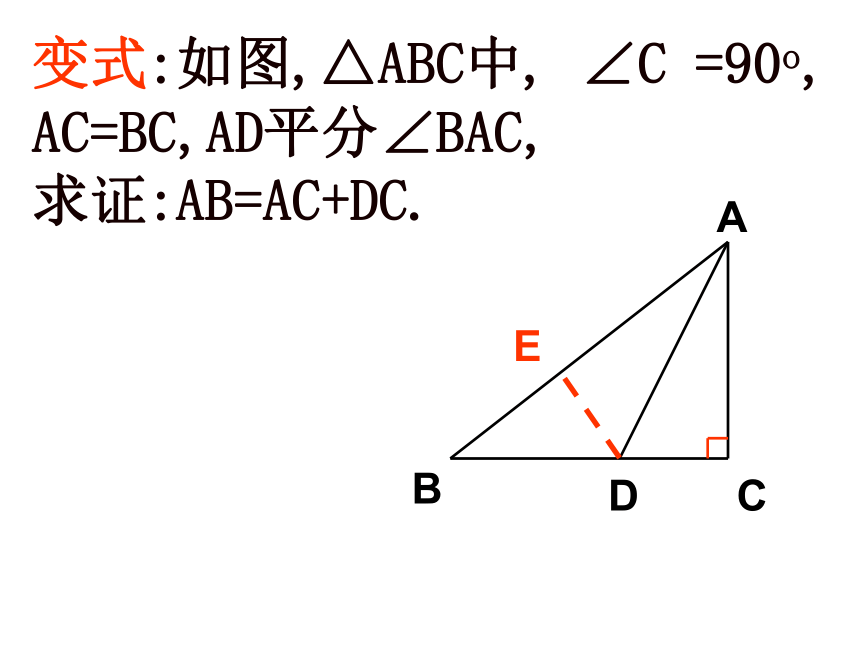
变式:如图,△ABC中, ∠C =90o,
AC=BC,AD平分∠BAC,
求证:AB=AC+DC.
A
C
D
B
E
A
C
D
B
E
练习:如图,四边形ABCD中, ∠A= ∠D =90o,其中BE、CE均是角平分线,求证:BC=AB+CD.
F
F
思考:你从本题中还能得到哪些结论?
截长补短
(1)小王同学延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
例3、如图,AD是△ABC的中线,求证:AB+AC>2AD
E
倍长中线
变式:已知,△ABC中,AB=4cm,
AC=6 cm,BD是AC边上的中线,
求AD的取值范围.
E
E
线段与角求相等,先找全等试试看。
图中有角平分线,可向两边作垂线。
线段计算和与差,巧用截长补短法。
三角形里有中线,延长中线=中线。
想作图形辅助线,切莫忘记要双添。
总结一下吧
---全等三角形中常见的辅助线
连线中考:
问题:如图1,四边形ABCD中, AB=AD ,∠BAD=120° ,∠B=∠ADC=90° .E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
(2)如图2,若四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.
提升:如图,AB=AE,AB⊥AE,AD=AC,AD⊥AC,点M为BC的中点,求证:DE=2AM.
知识要点:
判断三角形全等公理有SAS、ASA、AAS、SSS和HL
有些证明题要添加适当的辅助线构造合适的全等三角形,把条件相对集中起来,再进行等量代换,就可以化难为易了。
例1:如图,AB=AD,BC=DC,
求证:∠B=∠D.
A
C
B
D
A
C
B
D
N
M
变式:如图,AB=AC,BD=CD, M、N分别是BD、CD的中点,
求证:∠AMB= ∠ANC
连接
A
C
B
D
E
M
练习:如图,AB=AE,BC=ED, ∠B=∠E,AM⊥CD,
求证:点M是CD的中点.
你还能得到哪些结论?
A
C
D
B
例2:如图,在△ABC中,∠C=90o,
BC=10,BD=6,AD平分∠BAC,
求点D到AB的距离.
E
变式:如图,△ABC中, ∠C =90o,
AC=BC,AD平分∠BAC,
求证:AB=AC+DC.
A
C
D
B
E
A
C
D
B
E
练习:如图,四边形ABCD中, ∠A= ∠D =90o,其中BE、CE均是角平分线,求证:BC=AB+CD.
F
F
思考:你从本题中还能得到哪些结论?
截长补短
(1)小王同学延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
例3、如图,AD是△ABC的中线,求证:AB+AC>2AD
E
倍长中线
变式:已知,△ABC中,AB=4cm,
AC=6 cm,BD是AC边上的中线,
求AD的取值范围.
E
E
线段与角求相等,先找全等试试看。
图中有角平分线,可向两边作垂线。
线段计算和与差,巧用截长补短法。
三角形里有中线,延长中线=中线。
想作图形辅助线,切莫忘记要双添。
总结一下吧
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
