3.2.2角的度量课件
图片预览





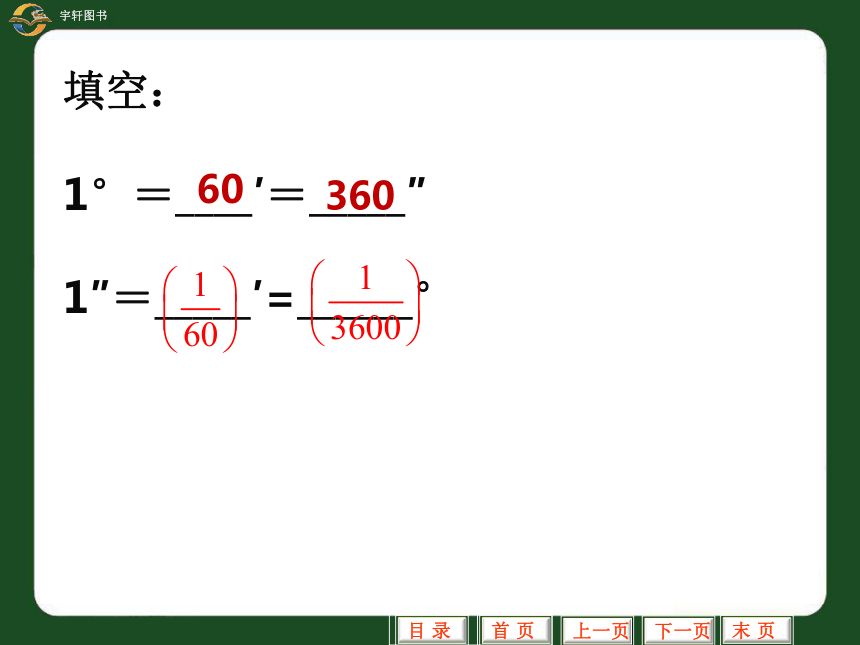





文档简介
(共30张PPT)
复习
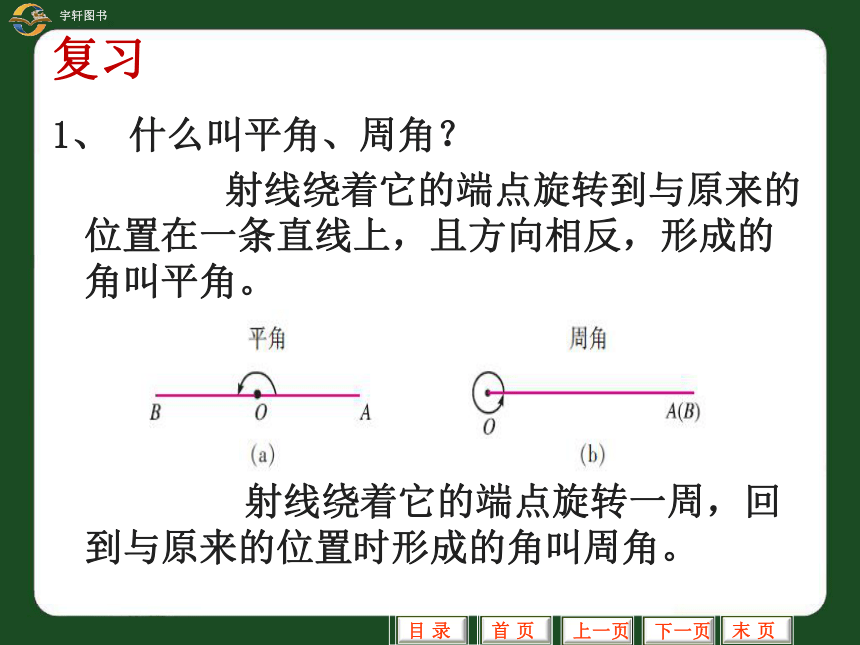
1、 什么叫平角、周角?
射线绕着它的端点旋转到与原来的位置在一条直线上,且方向相反,形成的角叫平角。
射线绕着它的端点旋转一周,回到与原来的位置时形成的角叫周角。
2、用量角器量角的度数时要注意什么?
角的一边
和量角器零
刻度线
重合
角的顶点
要和量角
器中心
点重合
从0开始读数
3、P 47图3---26,以大门为端点,向各景点作射线,得到了几个角?请你说出来,并量出各个角的大小。
B
A
D
C
新课引言
刚才同学们量得的角的单位用到了“度” “度”是什么意思呢?虽然小学我们学过用量角器量角的度数,但不明白其真正的含义。下面我们继续学习-----
3.2.2角的度量
主题讲解
主题一、 度、分、秒的意义及换算
(1)度、分、秒的意义:
把周角分成360等份,每一等份的角叫1度,记作:1°,把1°的 角再分成60等分,每一份的角叫1分,记作:1′,1′的 角再分成60等分,每一份的角叫1秒,记作:1″。
填空:
1°=____′=_____″
1″=_____′=______°
60
360
【例1】把56.43 化为度分秒
【解】 56.43 =56 +0.43 ,
0.43 =0.43×60′=25.8′=25′+0.8′
0.8′=0.8×60″=48″
所以,56.43 =56 25′48″
【点评】这个题目是把大单位化小单位,整个过程用乘法。
【变式练习】
45.56 =_____ ______′_______″.
【解】45.56 =45 +0.56 , 0.56 =0.56×60=33.6′=33′+0.6′
0.6′=0.6×60″=36″
所以45.56 =45 33′36′
45
33
36
【例2】用度表示 46 30′50″
【解
50″= ,
30.83′≈
所以,46 30′50″=46.51°
【点评】
把小单位化大单位应从小单位向上一级单位换算,除法运算一般保留两位小数。
【变式练习】用度表示30′18″
主题二、锐角、钝角、直角的概念
(1)观察下图,同一时刻北京、东京、巴黎三个地方的时间。你能求出这图中时针分针所成的角度吗?
主题二、锐角、钝角、直角的概念
(1)观察下图,同一时刻北京、东京、巴黎三个地方的时间。你能求出这图中时针分针所成的角度吗?
上面三个角有什么特点?
∠α恰好是平角的_____,叫直角;
∠β_______平角________直角,叫钝角;
∠γ____直角,叫锐角
一半
小于
大于
小于
(3)什么叫直角?什么叫锐角?什么叫钝角?
平角的一半(即90°的角)叫直角;
小于直角(即小于90°)的角叫锐角;
大于直角而小于平角的角叫钝角。
(4)填空:
1周角=___个平角=____个直角=_____ °
1个平角=____个直角=_____°,1个直角=___°
2
4
360
2
180
90
【例3】下列有关角的分类的说法正确的是( )
(1)大于90度的角是钝角;(2)小于平角的角叫钝角;(3)平角是两条边互为反向延长线的角;
(4)有公共顶点的两个直角组成平角;(5)钝角和锐角的差一定是锐角;(6)直角与锐角的和一定是钝角
A 1,B 2,C 3 D 4
【解】大于90度的角有可能大于平角,而大于平角的角
就不是钝角,所以(1)错;小于平角的角有可能小于
90度,而小于90度的角是锐角,所以B(2)错;(3)对
;(4)不对,如右图,两个直角有公
共顶点,但没有组成平角;(5)不对,
如一个钝角为185 ,一个锐角为10 ,
它们的差为175 ,就不是锐角;(6)正确。所以选B
主题三、 余角补角度概念及性质
1、余角补角的概念
做一做:测量P48的两个图形的四个角的大小,并求出它们的和。
∠1与∠2的和是一个平角,∠1与∠2叫互为补
角,∠1的补角是∠2,∠2的补角是∠1,∠3与
∠4的和等于90 ,∠3、∠4叫互为余角,∠3的余
角是∠4,∠4的余角是∠3,你能说说什么叫互为
余角,什么叫互为补角吗?
如果两个角的度数之和等于一个平角(即等于180°), 这两个角叫做互为补角, 或者说其中一个是另一个的补角(supplementary angle).
如果两个角的度数之和等于一个直角(即等于90°), 这两个角叫做互为余角, 或者说其中一个是另一个的余角(complementary angle).
【例4】一个角的补角比它的余角的2倍还大20度,求这个角。
【分析】根据“这个角补角=2×这个角的余角+20 ”,列方程求解;
【解】设这个角的度数为x,则这个角的补角为(180 -x),余角为(90 -x).
依题意,得:180-x=2(90-x)+20,解这个方程得:x=20
答:这个角的度数为20.
注意!列方程不要单位。
【变式练习】
下列说法正确的是( )
A 90度的角叫余角;
B 一个角的补角必是钝角;
C 一个锐角的余角必是锐角;
D 互补的两个角一个是钝角一个是锐角。
C
2、互为余角、互为补角的性质
想一想:
(1)如图:∠COD与∠BOC互余,∠AOB与∠BOC互余, ∠AOB与∠COD有什么关系?
【解】因为∠COD与∠BOC互余,
∠AOB与∠BOC互余
所以∠COD+∠BOC
=∠AOB+∠BOC=90
由等式性质得: ∠AOB=∠COD
(2)如图:∠A与∠D互补,∠C与∠D互补,则∠A与∠C有什么关系?由此你能得到什么规律?
【解】因为∠A与∠D互补,
∠C与∠D互补
所以∠A+∠D
=∠C+∠D=180
由等式性质得: ∠A=∠C
同角或等角的余角相等;同角的或等角的补角相等。
【例5】如图,直线AB、CD交于O,根据平角的定义可以得到:∠1+∠2=180 ,∠1+∠3=180 ,从而可以得到:∠2=∠3,根据是:_____________________.
同角的余角相等
【变式练习】
如图,O是直线AB上一点,∠BOD=90 ,∠COE=90 ,那么下列各式中错误的是
( )
A ∠AOC=∠DOE,
B ∠COD=∠BOE,
C ∠AOD=∠BOD,
D ∠BOE=∠AOC.
D
应用迁移
【例6】 如图,已知∠AOB与∠BOD互为余角,OC是∠BOD的角
平分线,∠AOB=29.66°
,求∠COD的度数.
(用度、分秒、表示)
【解】:因为∠AOB与∠BOD互为余角,
所以,∠BOD=90 -∠AOB
=90 -29.66 =63.34°
又因为OC是∠BOD的角平分线,
所以,∠COD=0.5∠BOD =0.5 × 63.34° =30.17 =30 10 ′12 ″
课堂练习
1、填空:
(1) 73°40′角的补角等于_____度___分; 锐角的补角一定是_______.
(2) 105°16′角的补角等于_____度____分; 钝角的补角一定是______.
(3) 90°角的补角等于______; 直角的补角一定是_____.
106
20
钝角
74
44
锐角
90
直角
2、 判断题
(1)大于直角的角叫钝角( ),
(2)一个锐角的补角一定大于这个锐角.
( )
(3)一个锐角的补角减去这个角的余角是直角。( )
(4)一个钝角与一个锐角的差一定是锐角
( )
×
√
√
×
3、下列各个角中一定是锐角的是( )
B
反思小结
这节课我们学习了哪些知识要点?最重要的是什么?
1、角的度量与角度单位的换算,要注意,角度换算是60进制,逢60进一。
2、互为余角和补角的概念与性质:两个角的和等于平角,这两个角互补,两个角的和等于直角,这两个角互余;同角或等角的补角相等,同角或等角的余角相等。
3、角的分类:锐角是指小于直角的角,钝角是指大于直角而小于平角的角。注意!大于直角的角不一定是钝角。
六 作业
P 50---51 A ,B
复习
1、 什么叫平角、周角?
射线绕着它的端点旋转到与原来的位置在一条直线上,且方向相反,形成的角叫平角。
射线绕着它的端点旋转一周,回到与原来的位置时形成的角叫周角。
2、用量角器量角的度数时要注意什么?
角的一边
和量角器零
刻度线
重合
角的顶点
要和量角
器中心
点重合
从0开始读数
3、P 47图3---26,以大门为端点,向各景点作射线,得到了几个角?请你说出来,并量出各个角的大小。
B
A
D
C
新课引言
刚才同学们量得的角的单位用到了“度” “度”是什么意思呢?虽然小学我们学过用量角器量角的度数,但不明白其真正的含义。下面我们继续学习-----
3.2.2角的度量
主题讲解
主题一、 度、分、秒的意义及换算
(1)度、分、秒的意义:
把周角分成360等份,每一等份的角叫1度,记作:1°,把1°的 角再分成60等分,每一份的角叫1分,记作:1′,1′的 角再分成60等分,每一份的角叫1秒,记作:1″。
填空:
1°=____′=_____″
1″=_____′=______°
60
360
【例1】把56.43 化为度分秒
【解】 56.43 =56 +0.43 ,
0.43 =0.43×60′=25.8′=25′+0.8′
0.8′=0.8×60″=48″
所以,56.43 =56 25′48″
【点评】这个题目是把大单位化小单位,整个过程用乘法。
【变式练习】
45.56 =_____ ______′_______″.
【解】45.56 =45 +0.56 , 0.56 =0.56×60=33.6′=33′+0.6′
0.6′=0.6×60″=36″
所以45.56 =45 33′36′
45
33
36
【例2】用度表示 46 30′50″
【解
50″= ,
30.83′≈
所以,46 30′50″=46.51°
【点评】
把小单位化大单位应从小单位向上一级单位换算,除法运算一般保留两位小数。
【变式练习】用度表示30′18″
主题二、锐角、钝角、直角的概念
(1)观察下图,同一时刻北京、东京、巴黎三个地方的时间。你能求出这图中时针分针所成的角度吗?
主题二、锐角、钝角、直角的概念
(1)观察下图,同一时刻北京、东京、巴黎三个地方的时间。你能求出这图中时针分针所成的角度吗?
上面三个角有什么特点?
∠α恰好是平角的_____,叫直角;
∠β_______平角________直角,叫钝角;
∠γ____直角,叫锐角
一半
小于
大于
小于
(3)什么叫直角?什么叫锐角?什么叫钝角?
平角的一半(即90°的角)叫直角;
小于直角(即小于90°)的角叫锐角;
大于直角而小于平角的角叫钝角。
(4)填空:
1周角=___个平角=____个直角=_____ °
1个平角=____个直角=_____°,1个直角=___°
2
4
360
2
180
90
【例3】下列有关角的分类的说法正确的是( )
(1)大于90度的角是钝角;(2)小于平角的角叫钝角;(3)平角是两条边互为反向延长线的角;
(4)有公共顶点的两个直角组成平角;(5)钝角和锐角的差一定是锐角;(6)直角与锐角的和一定是钝角
A 1,B 2,C 3 D 4
【解】大于90度的角有可能大于平角,而大于平角的角
就不是钝角,所以(1)错;小于平角的角有可能小于
90度,而小于90度的角是锐角,所以B(2)错;(3)对
;(4)不对,如右图,两个直角有公
共顶点,但没有组成平角;(5)不对,
如一个钝角为185 ,一个锐角为10 ,
它们的差为175 ,就不是锐角;(6)正确。所以选B
主题三、 余角补角度概念及性质
1、余角补角的概念
做一做:测量P48的两个图形的四个角的大小,并求出它们的和。
∠1与∠2的和是一个平角,∠1与∠2叫互为补
角,∠1的补角是∠2,∠2的补角是∠1,∠3与
∠4的和等于90 ,∠3、∠4叫互为余角,∠3的余
角是∠4,∠4的余角是∠3,你能说说什么叫互为
余角,什么叫互为补角吗?
如果两个角的度数之和等于一个平角(即等于180°), 这两个角叫做互为补角, 或者说其中一个是另一个的补角(supplementary angle).
如果两个角的度数之和等于一个直角(即等于90°), 这两个角叫做互为余角, 或者说其中一个是另一个的余角(complementary angle).
【例4】一个角的补角比它的余角的2倍还大20度,求这个角。
【分析】根据“这个角补角=2×这个角的余角+20 ”,列方程求解;
【解】设这个角的度数为x,则这个角的补角为(180 -x),余角为(90 -x).
依题意,得:180-x=2(90-x)+20,解这个方程得:x=20
答:这个角的度数为20.
注意!列方程不要单位。
【变式练习】
下列说法正确的是( )
A 90度的角叫余角;
B 一个角的补角必是钝角;
C 一个锐角的余角必是锐角;
D 互补的两个角一个是钝角一个是锐角。
C
2、互为余角、互为补角的性质
想一想:
(1)如图:∠COD与∠BOC互余,∠AOB与∠BOC互余, ∠AOB与∠COD有什么关系?
【解】因为∠COD与∠BOC互余,
∠AOB与∠BOC互余
所以∠COD+∠BOC
=∠AOB+∠BOC=90
由等式性质得: ∠AOB=∠COD
(2)如图:∠A与∠D互补,∠C与∠D互补,则∠A与∠C有什么关系?由此你能得到什么规律?
【解】因为∠A与∠D互补,
∠C与∠D互补
所以∠A+∠D
=∠C+∠D=180
由等式性质得: ∠A=∠C
同角或等角的余角相等;同角的或等角的补角相等。
【例5】如图,直线AB、CD交于O,根据平角的定义可以得到:∠1+∠2=180 ,∠1+∠3=180 ,从而可以得到:∠2=∠3,根据是:_____________________.
同角的余角相等
【变式练习】
如图,O是直线AB上一点,∠BOD=90 ,∠COE=90 ,那么下列各式中错误的是
( )
A ∠AOC=∠DOE,
B ∠COD=∠BOE,
C ∠AOD=∠BOD,
D ∠BOE=∠AOC.
D
应用迁移
【例6】 如图,已知∠AOB与∠BOD互为余角,OC是∠BOD的角
平分线,∠AOB=29.66°
,求∠COD的度数.
(用度、分秒、表示)
【解】:因为∠AOB与∠BOD互为余角,
所以,∠BOD=90 -∠AOB
=90 -29.66 =63.34°
又因为OC是∠BOD的角平分线,
所以,∠COD=0.5∠BOD =0.5 × 63.34° =30.17 =30 10 ′12 ″
课堂练习
1、填空:
(1) 73°40′角的补角等于_____度___分; 锐角的补角一定是_______.
(2) 105°16′角的补角等于_____度____分; 钝角的补角一定是______.
(3) 90°角的补角等于______; 直角的补角一定是_____.
106
20
钝角
74
44
锐角
90
直角
2、 判断题
(1)大于直角的角叫钝角( ),
(2)一个锐角的补角一定大于这个锐角.
( )
(3)一个锐角的补角减去这个角的余角是直角。( )
(4)一个钝角与一个锐角的差一定是锐角
( )
×
√
√
×
3、下列各个角中一定是锐角的是( )
B
反思小结
这节课我们学习了哪些知识要点?最重要的是什么?
1、角的度量与角度单位的换算,要注意,角度换算是60进制,逢60进一。
2、互为余角和补角的概念与性质:两个角的和等于平角,这两个角互补,两个角的和等于直角,这两个角互余;同角或等角的补角相等,同角或等角的余角相等。
3、角的分类:锐角是指小于直角的角,钝角是指大于直角而小于平角的角。注意!大于直角的角不一定是钝角。
六 作业
P 50---51 A ,B
同课章节目录
