七年级数学7.1.1 三角形的边
文档属性
| 名称 | 七年级数学7.1.1 三角形的边 |  | |
| 格式 | zip | ||
| 文件大小 | 985.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-11 20:50:23 | ||
图片预览







文档简介
(共34张PPT)
如以下图所示,你能够得到什么几何图形?
你还能举出生活中的这种图形的形象吗?
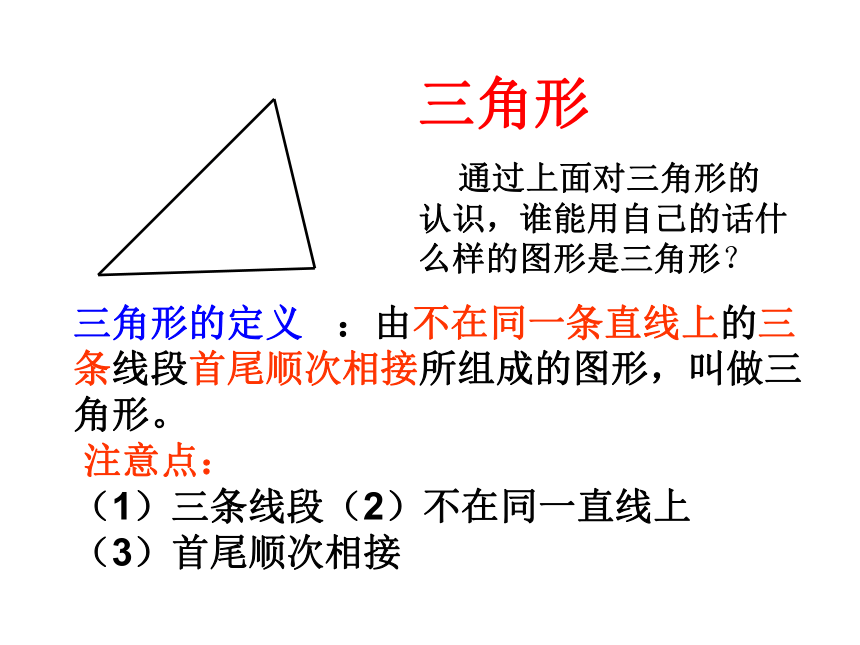
三角形
通过上面对三角形的认识,谁能用自己的话什么样的图形是三角形?
三角形的定义 :由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形。
注意点:
(1)三条线段(2)不在同一直线上
(3)首尾顺次相接
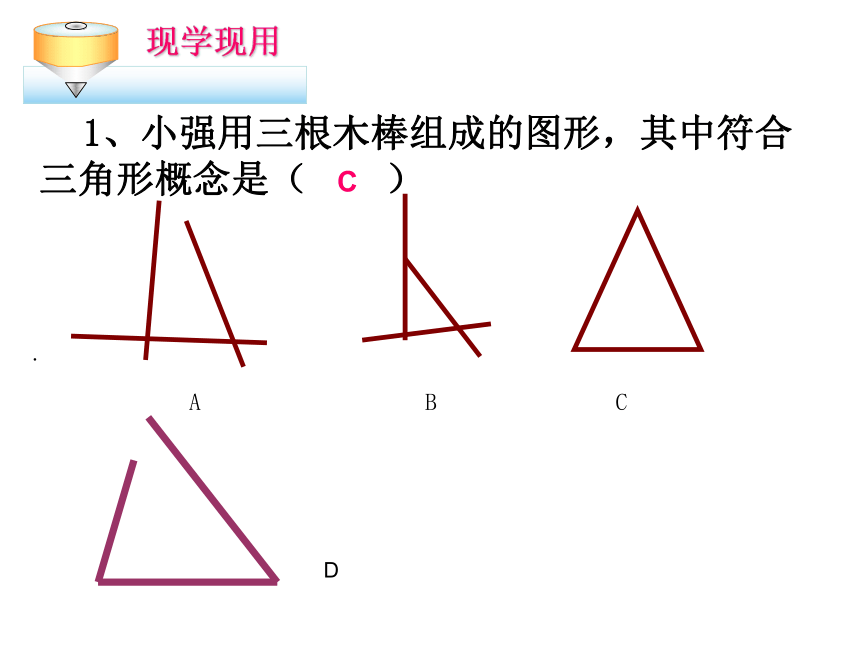
1、小强用三根木棒组成的图形,其中符合三角形概念是( )
B
A
C
现学现用
C
.
D
A
B
C
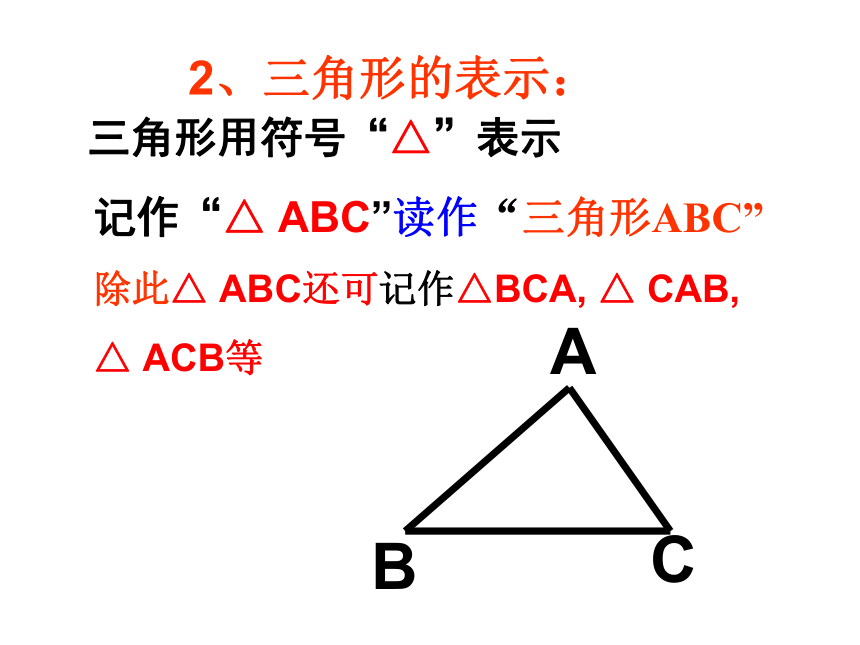
三角形用符号“△”表示
记作“△ ABC”读作“三角形ABC”
除此△ ABC还可记作△BCA, △ CAB,
△ ACB等
2、三角形的表示:
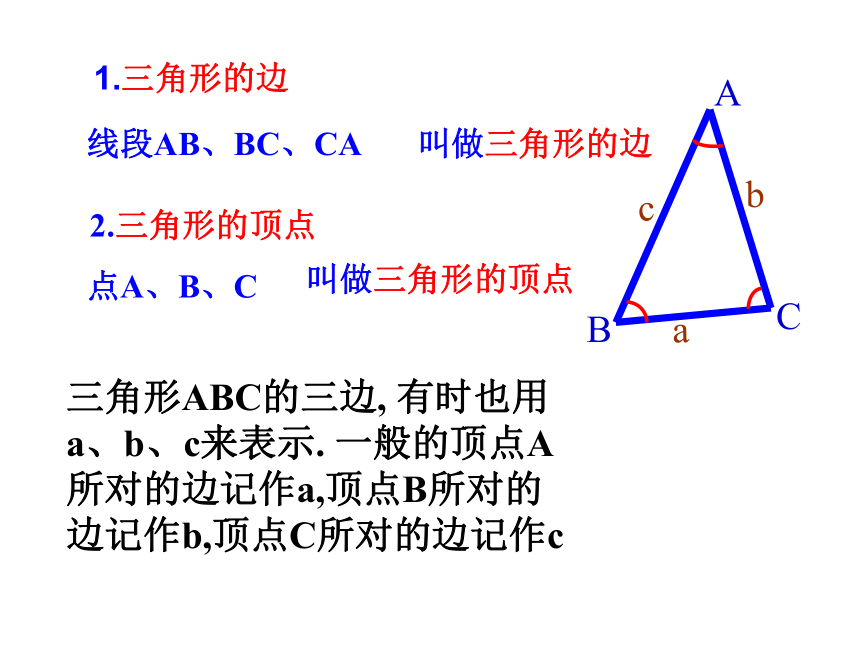
三角形ABC的三边, 有时也用
a、b、c来表示. 一般的顶点A
所对的边记作a,顶点B所对的
边记作b,顶点C所对的边记作c
线段AB、BC、CA
叫做三角形的边
点A、B、C
叫做三角形的顶点
A
C
B
a
b
c
2.三角形的顶点
1.三角形的边
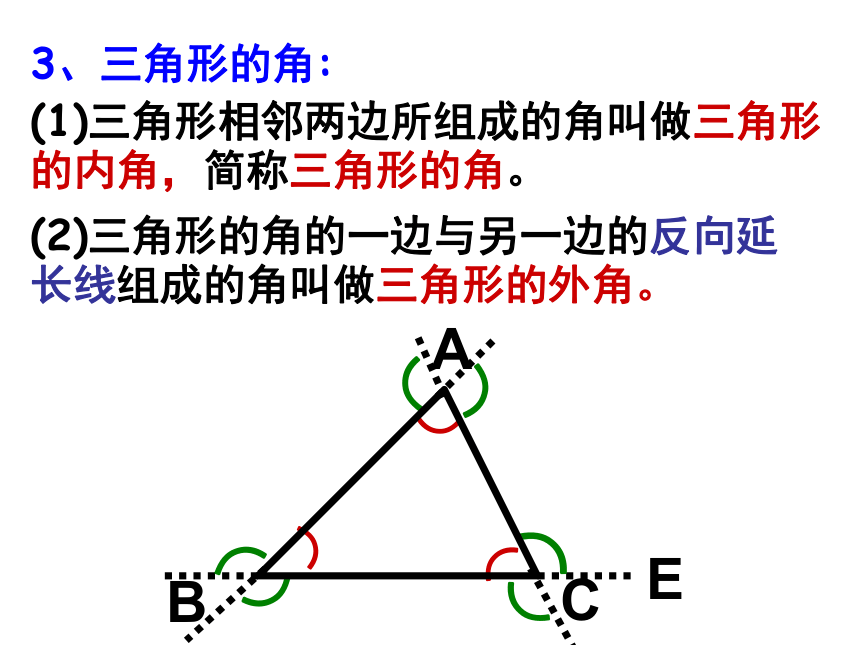
3、三角形的角:
(1)三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
)
)
)
(2)三角形的角的一边与另一边的反向延长线组成的角叫做三角形的外角。
)
)
)
)
)
)
A
B
C
E
例 说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边.
Q
F
E
P
G
H
练习:
1.读出图中的各个三角形.
A
D
B
E
C
A
D
C
B
E
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE
4.以∠D为角的三角形有哪些?
△ BCD、 △DEC
5.说出其中ΔBCD的三个角
∠BCD 、 ∠CBD 、∠D
1. 三角形按照三个角的大小都有哪些三角形呢?
想一想
锐角三角形
直角三角形
钝角三角形
2.三角形按照三条边长的大小关系又有哪些三角形呢?
不等边三角形
等腰三角形
等边三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
等腰三角形
三角形的分类
底边和腰不相等的等腰三角形
等边三角形
相等的两条边都叫腰,
另一边叫做底,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角。
腰
腰
底
顶角
底角
底角
如图三角形中,假设有一只小虫要从点B出发沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
A
B
C
路线1:由点B到点C
路线2:由点B到点A,再由点A到点C。
两条路线长分别是BC,AB+AC.
由“两点之间,线段最短” 可以得AB+AC>BC
同理可得:AC+BC>AB,AB+BC>AC
三角形的三边有这样的关系:
三角形两边的和大于第三边
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断 方法?
思 考:
只要选取两条较短的线段,求出和再与最长的线段比较 ,和较大,则可以;否则不能组成三角形。
2、下列长度的三条线段能否组成三角形?
为什么?
(1)3 , 4, 8 (2)5 , 6 , 11 (3)5 , 6, 10
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断方法?
思考
例 用一条长为18cm的细绳围成一个等腰三角形。
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为4cm的等腰三角形吗?为什么?
1.已知等腰三角形的两边长分别为3和6,则它的周长为( )
A.9 B.12
C.15 D.12或15
2.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A.2cm B.3cm
C.4cm D.5cm
3.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
4、已知等腰三角形的一边等于7,另一边等于8,求它的周长?
5、已知等腰三角形的一边等于3,另一边等于8,求它的周长?
1、某村庄和小学分别位于两条交叉的大路边(如图)。可是,每年冬天麦田弄不好就会走出一条小路来。你说小学生为什么会这样走呢?
村庄
学校
麦
田
草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。
A
D
C
B
H
H′
1.你认为这个H应该在什么位置?大胆设想!
2.到A、C距离和最小的点在哪儿?到B、D
有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
答:不能。如果此人一步能走3米多,由三角形三边的关系得,此人两腿得长大于3米多,这与实际情况相矛盾,所以它一步不能走3米多。
本节课的学习你有哪些收获?
1.三角形的概念
2.三角形的表示方法
3.三角形的分类
4.三角形三边之间的关系
如以下图所示,你能够得到什么几何图形?
你还能举出生活中的这种图形的形象吗?
三角形
通过上面对三角形的认识,谁能用自己的话什么样的图形是三角形?
三角形的定义 :由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形。
注意点:
(1)三条线段(2)不在同一直线上
(3)首尾顺次相接
1、小强用三根木棒组成的图形,其中符合三角形概念是( )
B
A
C
现学现用
C
.
D
A
B
C
三角形用符号“△”表示
记作“△ ABC”读作“三角形ABC”
除此△ ABC还可记作△BCA, △ CAB,
△ ACB等
2、三角形的表示:
三角形ABC的三边, 有时也用
a、b、c来表示. 一般的顶点A
所对的边记作a,顶点B所对的
边记作b,顶点C所对的边记作c
线段AB、BC、CA
叫做三角形的边
点A、B、C
叫做三角形的顶点
A
C
B
a
b
c
2.三角形的顶点
1.三角形的边
3、三角形的角:
(1)三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
)
)
)
(2)三角形的角的一边与另一边的反向延长线组成的角叫做三角形的外角。
)
)
)
)
)
)
A
B
C
E
例 说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边.
Q
F
E
P
G
H
练习:
1.读出图中的各个三角形.
A
D
B
E
C
A
D
C
B
E
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE
4.以∠D为角的三角形有哪些?
△ BCD、 △DEC
5.说出其中ΔBCD的三个角
∠BCD 、 ∠CBD 、∠D
1. 三角形按照三个角的大小都有哪些三角形呢?
想一想
锐角三角形
直角三角形
钝角三角形
2.三角形按照三条边长的大小关系又有哪些三角形呢?
不等边三角形
等腰三角形
等边三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
等腰三角形
三角形的分类
底边和腰不相等的等腰三角形
等边三角形
相等的两条边都叫腰,
另一边叫做底,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角。
腰
腰
底
顶角
底角
底角
如图三角形中,假设有一只小虫要从点B出发沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
A
B
C
路线1:由点B到点C
路线2:由点B到点A,再由点A到点C。
两条路线长分别是BC,AB+AC.
由“两点之间,线段最短” 可以得AB+AC>BC
同理可得:AC+BC>AB,AB+BC>AC
三角形的三边有这样的关系:
三角形两边的和大于第三边
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断 方法?
思 考:
只要选取两条较短的线段,求出和再与最长的线段比较 ,和较大,则可以;否则不能组成三角形。
2、下列长度的三条线段能否组成三角形?
为什么?
(1)3 , 4, 8 (2)5 , 6 , 11 (3)5 , 6, 10
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断方法?
思考
例 用一条长为18cm的细绳围成一个等腰三角形。
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为4cm的等腰三角形吗?为什么?
1.已知等腰三角形的两边长分别为3和6,则它的周长为( )
A.9 B.12
C.15 D.12或15
2.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A.2cm B.3cm
C.4cm D.5cm
3.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
4、已知等腰三角形的一边等于7,另一边等于8,求它的周长?
5、已知等腰三角形的一边等于3,另一边等于8,求它的周长?
1、某村庄和小学分别位于两条交叉的大路边(如图)。可是,每年冬天麦田弄不好就会走出一条小路来。你说小学生为什么会这样走呢?
村庄
学校
麦
田
草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。
A
D
C
B
H
H′
1.你认为这个H应该在什么位置?大胆设想!
2.到A、C距离和最小的点在哪儿?到B、D
有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
答:不能。如果此人一步能走3米多,由三角形三边的关系得,此人两腿得长大于3米多,这与实际情况相矛盾,所以它一步不能走3米多。
本节课的学习你有哪些收获?
1.三角形的概念
2.三角形的表示方法
3.三角形的分类
4.三角形三边之间的关系
