9.2用样本估计总体-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义
文档属性
| 名称 | 9.2用样本估计总体-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义 |  | |
| 格式 | docx | ||
| 文件大小 | 1006.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 19:41:33 | ||
图片预览



文档简介
9.2 用样本估计总体
【知识点一】频率分布直方图
作频率分布直方图的步骤
1.求极差:极差为一组数据中最大值与最小值的差.
2.决定组距与组数
将数据分组时,一般取等长组距,并且组距应力求“取整”,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.
3.将数据分组
4.列频率分布表
各小组的频率=.
5.画频率分布直方图
纵轴表示,实际上就是频率分布直方图中各小长方形的高度,小长方形的面积=组距×=频率.
【知识点二】常见统计图表的特点与区别
扇形图主要用于直观描述各类数据占总数的比例,条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率,条形图适用于描述离散型数据,直方图适用于描述连续型数据.折线图主要用于描述数据随时间的变化趋势.
【知识点三】百分位数
1.百分位数定义:一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
2.常用的百分位数
(1)四分位数:第25百分位数,第50百分位数,第75百分位数.
(2)其它常用的百分位数:第1百分位数,第5百分位数,第95百分位数,第99百分位数.
3.计算一组n个数据的第p百分位数的一般步骤如下:
第1步,按从小到大排列原始数据;
第2步,计算i=n×p%;
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
【知识点四】众数、中位数、平均数
1.众数:一组数据中出现次数最多的数.
2.中位数:把一组数据按从小到大(或从大到小)的顺序排列,处在中间位置的数(或中间两个数的平均数)叫做这组数据的中位数.
3.平均数:如果n个数x1,x2,…,xn,那么=(x1+x2+…+xn)叫做这n个数的平均数.
【知识点五】总体集中趋势的估计
1.平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势.
2.一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
【知识点六】频率分布直方图中平均数、中位数、众数的求法
1.样本平均数:可以用每个小矩形底边中点的横坐标与小矩形面积的乘积之和近似代替.
2.在频率分布直方图中,中位数左边和右边的直方图的面积应相等.
3.将最高小矩形所在的区间中点作为众数的估计值.
【知识点七】方差、标准差
1.假设一组数据为x1,x2,…xn,则这组数据的平均数=,方差为s2=(xi-)2,标准差
2.如果总体中所有个体的变量值分别为Y1,Y2,…,YN,总体平均数为,则称S2=(Yi-)2为总体方差,S=为总体标准差.
如果总体的N个变量值中,不同的值共有k(k≤N)个,不妨记为Y1,Y2,…,Yk,其中Yi出现的频数为fi(i=1,2,…,k),则总体方差为S2=(Yi-)2.
3.如果一个样本中个体的变量值分别为y1,y2,…,yn,样本平均数为,则称s2=(yi-)2为样本方差,s=为样本标准差.
4.标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.
【例1-1】一个容量为100的样本,其数据的分组与各组的频数如下:
分组
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
[60,70]
频数
12
13
24
15
16
13
7
则样本数据落在[10,40)上的频率为( )
A.0.13
B.0.39
C.0.52
D.0.64
【变式1】容量为100的某个样本,数据拆分为10组,若前七组频率之和为0.79,而剩下的三组的频率依次相差0.05,则剩下的三组中频率最大的一组频率为________.
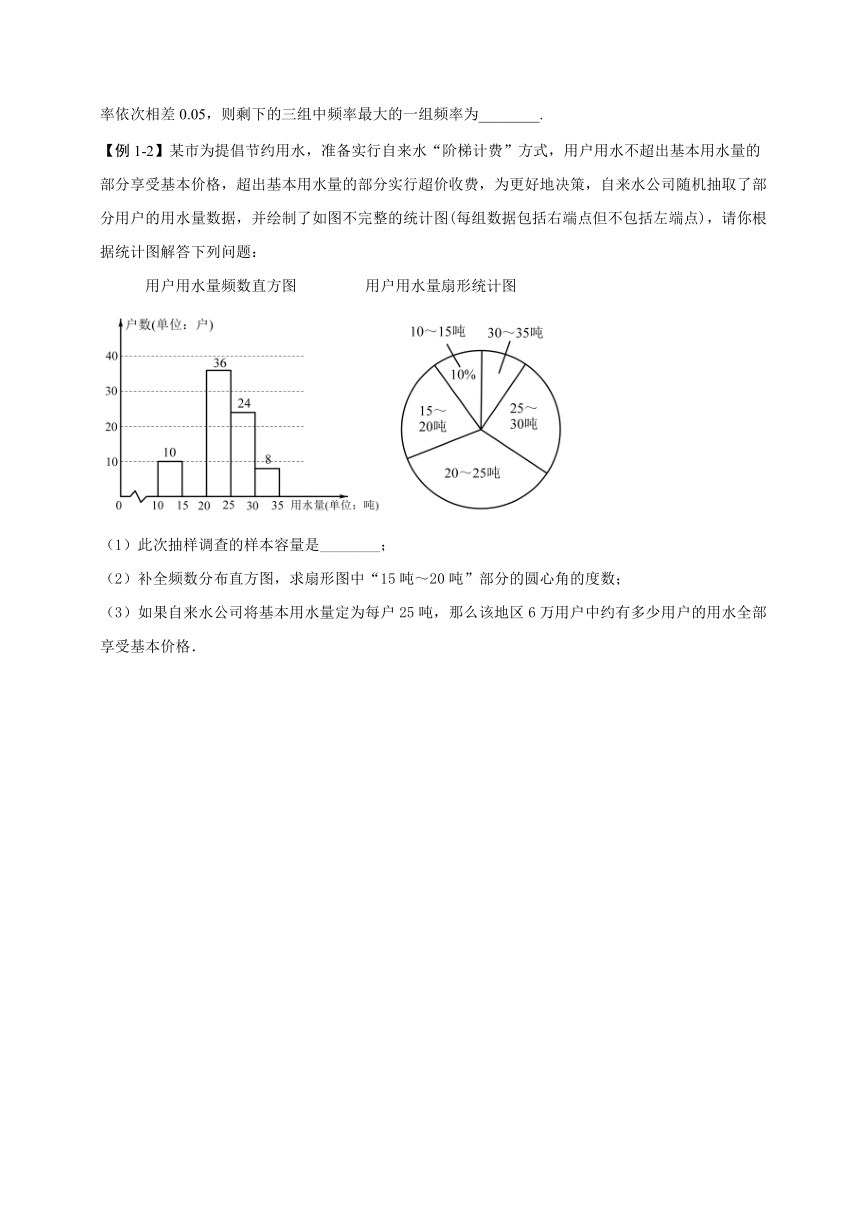
【例1-2】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
用户用水量频数直方图
用户用水量扇形统计图
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格.
【变式1】某市2020年4月1日~4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,
77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,空间质量为良;在101~150之间时,空间质量为轻微污染;在151~200之间时,空间质量为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
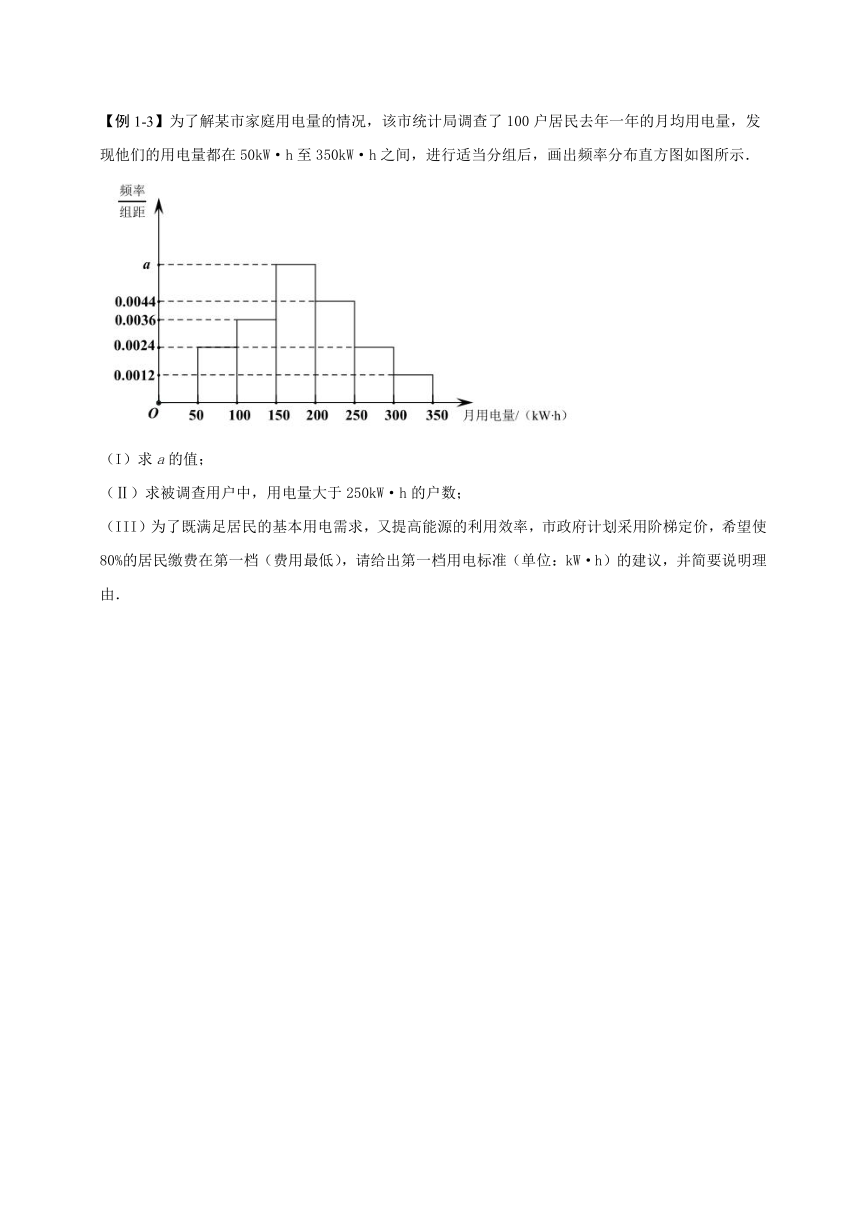
【例1-3】为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50kW·h至350kW·h之间,进行适当分组后,画出频率分布直方图如图所示.
(I)求a的值;
(Ⅱ)求被调查用户中,用电量大于250kW·h的户数;
(III)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,希望使80%的居民缴费在第一档(费用最低),请给出第一档用电标准(单位:kW·h)的建议,并简要说明理由.
【变式1】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的比例;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论).
【例2-1】(1)给出如图所示的三幅统计图及四个命题:
①从折线统计图能看出世界人口的变化情况;
②2050年非洲人口将达到大约15亿;
③2050年亚洲人口比其他各洲人口的总和还要多;
④从1957年到2050年各洲中北美洲人口增长速度最慢.
其中命题正确的有( )
A.①②
B.①③
C.①④
D.②④
【变式1】根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)的柱形图.以下结论不正确的是( )
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量呈增加趋势
【例2-2】已知一组数据为第百分位数是(
)
A.
B.
C.
D.
【变式1】数据1,2,3,4,5,6的60%分位数为(
)
A.3
B.3.5
C.3.6
D.4
【变式2】“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间内的一个数来表示,该数越接近10表示满意程度越高,现随机抽取6位小区居号,他们的幸福感指数分别为5,6,7,8,9,5,则这组数据的第80百分位数是(
)
A.7
B.7.5
C.8
D.9
【例3-1】在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(单位:m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的众数、中位数与平均数.
【变式1】某学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各1人,则该小组数学成绩的平均数、众数、中位数分别为( )
A.85,85,85
B.87,85,86
C.87,85,85
D.87,85,90
【例3-2】因受新冠疫情的影响,某企业的产品销售面临困难.为了改变现状,该企业欲借助电商和“网红”直播带货扩大销售.受网红效应的影响,产品销售取得了较好的效果.现将该企业一段时间内网上销售的日销售额统计整理后绘制成如下图所示的频率分布直方图:
请根据图中所给数据,求:
(1)实数a的值;
(2)该企业网上销售日销售额的众数和中位数;
(3)该企业在统计时间段内网上销售日销售额的平均数.
【变式1】校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的优秀率(80分及以上为及格)和平均分.
【变式2】某城市户居民的月平均用水量(单位:吨),以分组的频率分布直方图如图.
(1)求直方图中的值;并估计出月平均用水量的众数.
(2)求月平均用水量的中位数及平均数;
(3)在月平均用水量为,,,的四组用户中,用分层抽样的方法抽取22户居民,则应在这一组的用户中抽取多少户?
(4)在第(3)问抽取的样本中,从这两组中再随机抽取2户,深入调查,则所抽取的两户不是来自同一个组的概率是多少?
【例4-1】如图所示的四组数据,标准差最小的是(
)
A.
B.
C.
D.
【变式1】从甲、乙两种玉米苗中各抽取10株,分别测得它们的株高如下(单位:cm):
甲 25 41 40 37 22 14 19 39 21 42
乙 27 16 44 27 44 16 40 40 16 40
求:(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
【例4-2】甲、乙两支田径队体检结果为:甲队的体重的平均数为60
kg,方差为200,乙队体重的平均数为70
kg,方差为300,又已知甲、乙两队的队员人数之比为1∶4,那么甲、乙两队全部队员的平均体重和方差分别是什么?
【变式1】某培训机构在假期招收了A,B两个数学补习班,A班10人,B班30人,经过一周的补习后进行了一次测试,在该测试中,A班的平均成绩为130分,方差为115,B班的平均成绩为110分,方差为215.求在这次测试中全体学生的平均成绩和方差.
课后练习题
1.为了解学生课外阅读的情况,随机统计了名学生的课外阅读时间,所得数据都在中,其频率分布直方图如图所示.已知在中的频数为100,则的值是(
)
A.500
B.1000
C.10000
D.25000
2.某工厂对一批产品进行了抽样检测.下图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[90,100],样品数据分组为,,,,.已知样本中产品净重小于94克的个数为36,则样本中净重大于或等于92克并且小于98克的产品的个数是(
)
A.
B.
C.
D.
3.“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的,全世界近人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨):一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使的居民每月的用水不按议价收费,估计的值,并说明理由.
4.随机观测生产某种零件的某工厂名工人的日加工零件数(单位:件),获得数据如下:、、、、、、、、、、、、、、、、、、、、、、、、,根据上述数据得到样本的频率分布表如下:
分组
频数
频率
(1)确定样本频率分布表中、、和的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取人,至少有人的日加工零件数落在区间的概率.
5.数据10,9,8,7,6,5,4,3,2,1的25%分位数、80%分位数分别是_______;
6.2020年宿州市某中学参加高中数学建模(应用)能力测试,高一年级有60人,高二年级有40人.高一的平均成绩为70分,高二的平均成绩为80分,则参加测试的100名学生的平均成绩为(
)
A.72分
B.73分
C.74分
D.75分
7.根据气象学上的标准,连续天的日平均气温低于即为入冬.现有甲、乙、丙、丁四地连续天的日平均温度的记录数据(记录数据都是正整数):
①甲地:个数据的中位数为,众数为;
②乙地:个数据的平均数为,极差为;
③丙地:个数据的平均数为,中位数为;
④丁地:个数据的平均数为,方差小于.
则肯定进入冬季的地区是(
)
A.甲地
B.乙地
C.丙地
D.丁地
8.某地教育部门对某学校学生的阅读素养进行检测,在该校随机抽取了名学生进行检测,实行百分制,现将所得的成绩按照,分成6组,并根据所得数据作出了如下所示的频数与频率的统计表和频率分布直方图.
分组
频数
频率
25
0.30
10
0.10
合计
1
(1)求出表中及图中的值;
(2)估计该校学生阅读素养的成绩中位数以及平均数.
9.(多选)国家为了实现经济“双循环”大战略,对东部和西部地区的多个县市的某一类经济指标进行调查,得出东部,西部两组数据的茎叶图如图所示,则下列结论正确的是(
)
A.西部的平均数为13.3
B.东部的极差小于西部的极差
C.东部的30%分位数是11.6
D.东部的众数比西部的众数小
10.为庆祝国庆节,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名,将其成绩(成绩均为整数)分成[40,50),[50,60),…,[90,100]六组,并画出如图所示的部分频率分布直方图,观察图形,回答下列问题:
(1)求第四组的频率,并补全这个频率分布直方图;
(2)请根据频率分布直方图,估计样本的中位数和方差.(每组数据以区间的中点值为代表).
9.2 用样本估计总体
【知识点一】频率分布直方图
作频率分布直方图的步骤
1.求极差:极差为一组数据中最大值与最小值的差.
2.决定组距与组数
将数据分组时,一般取等长组距,并且组距应力求“取整”,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.
3.将数据分组
4.列频率分布表
各小组的频率=.
5.画频率分布直方图
纵轴表示,实际上就是频率分布直方图中各小长方形的高度,小长方形的面积=组距×=频率.
【知识点二】常见统计图表的特点与区别
扇形图主要用于直观描述各类数据占总数的比例,条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率,条形图适用于描述离散型数据,直方图适用于描述连续型数据.折线图主要用于描述数据随时间的变化趋势.
【知识点三】百分位数
1.百分位数定义:一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
2.常用的百分位数
(1)四分位数:第25百分位数,第50百分位数,第75百分位数.
(2)其它常用的百分位数:第1百分位数,第5百分位数,第95百分位数,第99百分位数.
3.计算一组n个数据的第p百分位数的一般步骤如下:
第1步,按从小到大排列原始数据;
第2步,计算i=n×p%;
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
【知识点四】众数、中位数、平均数
1.众数:一组数据中出现次数最多的数.
2.中位数:把一组数据按从小到大(或从大到小)的顺序排列,处在中间位置的数(或中间两个数的平均数)叫做这组数据的中位数.
3.平均数:如果n个数x1,x2,…,xn,那么=(x1+x2+…+xn)叫做这n个数的平均数.
【知识点五】总体集中趋势的估计
1.平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势.
2.一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
【知识点六】频率分布直方图中平均数、中位数、众数的求法
1.样本平均数:可以用每个小矩形底边中点的横坐标与小矩形面积的乘积之和近似代替.
2.在频率分布直方图中,中位数左边和右边的直方图的面积应相等.
3.将最高小矩形所在的区间中点作为众数的估计值.
【知识点七】方差、标准差
1.假设一组数据为x1,x2,…xn,则这组数据的平均数=,方差为s2=(xi-)2,标准差
2.如果总体中所有个体的变量值分别为Y1,Y2,…,YN,总体平均数为,则称S2=(Yi-)2为总体方差,S=为总体标准差.
如果总体的N个变量值中,不同的值共有k(k≤N)个,不妨记为Y1,Y2,…,Yk,其中Yi出现的频数为fi(i=1,2,…,k),则总体方差为S2=(Yi-)2.
3.如果一个样本中个体的变量值分别为y1,y2,…,yn,样本平均数为,则称s2=(yi-)2为样本方差,s=为样本标准差.
4.标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.
【例1-1】一个容量为100的样本,其数据的分组与各组的频数如下:
分组
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
[60,70]
频数
12
13
24
15
16
13
7
则样本数据落在[10,40)上的频率为( )
A.0.13
B.0.39
C.0.52
D.0.64
【答案】C
【解析】由题意可知样本数据落在[10,40)的频数为13+24+15=52,所以频率为=0.52.故选C.
【变式1】容量为100的某个样本,数据拆分为10组,若前七组频率之和为0.79,而剩下的三组的频率依次相差0.05,则剩下的三组中频率最大的一组频率为________.
【答案】0.12
【解析】设剩下的三组中频率最大的一组的频率为x,则另两组的频率分别为x-0.05,x-0.1,而由频率和为1得0.79+(x-0.05)+(x-0.1)+x=1,解得x=0.12.
【例1-2】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
用户用水量频数直方图
用户用水量扇形统计图
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格.
【答案】(1)答案见解析;(2)答案见解析,79.2°;(3)4.08万户.
【解析】(1);
(2)用水15~20吨的户数为100-10-36-24-8=22(户),
“15~20吨”部分的圆心角的度数为
(3)(万户)
所以该地区6万用户中约有4.08万户的用水全部享受基本价格.
【变式1】某市2020年4月1日~4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,
77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,空间质量为良;在101~150之间时,空间质量为轻微污染;在151~200之间时,空间质量为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
【答案】(1)频率分布表见解析;(2)频率分布直方图见解析;(3)该市空气质量有待进一步改善.
【解析】(1)频率分布表
分组
频数
频率
分组
频数
频率
[41,51)
2
[81,91)
10
[51,61)
1
[91,101)
5
[61,71)
4
[101,111)
2
[71,81)
6
(2)频率分布直方图
(3)答对下述两条中的一条即可:
①该市一个月中空气污染指数有2天处于优的水平,占当月天数的;
有26天处于良的水平,占当月天数的;
处于优或良的天数共有28天,占当月天数的.说明该市空气质量基本良好.
②轻微污染有2天,占当月天数的.污染指数在80以上的接近轻微污染的天数有
15天,加上处于轻微污染的天数,共有17天,占当月天数的,超过50%.
说明该市空气质量有待进一步改善.
【例1-3】为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50kW·h至350kW·h之间,进行适当分组后,画出频率分布直方图如图所示.
(I)求a的值;
(Ⅱ)求被调查用户中,用电量大于250kW·h的户数;
(III)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,希望使80%的居民缴费在第一档(费用最低),请给出第一档用电标准(单位:kW·h)的建议,并简要说明理由.
【答案】(I);(Ⅱ);(III)
kW·h.
【解析】(1)因为,所以;
(2)根据频率分布直方图可知:“用电量大于250kW·h”的频率为,
所以用电量大于250kW·h的户数为:,
故用电量大于250kW·h有户;
(3)因为前三组的频率和为:,
前四组的频率之和为,
所以频率为时对应的数据在第四组,
所以第一档用电标准为:kW·h.
故第一档用电标准为
kW·h.
【变式1】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的比例;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论).
【解析】(1)根据频数分布表知,100名学生中一周课外阅读时间不少于12小时的学生共有6+2+2=10(名),
所以样本中的学生一周课外阅读时间少于12小时的频率是1-=0.9.
故从该校随机选取一名学生,估计其该周课外阅读时间少于12小时的比例为0.9.
(2)课外阅读时间落在[4,6)组内的有17人,频率为0.17,所以a===0.085.
课外阅读时间落在[8,10)组内的有25人,频率为0.25,
所以b===0.125.
(3)样本中的100名学生该周课外阅读时间的平均数在第4组.
【例2-1】(1)给出如图所示的三幅统计图及四个命题:
①从折线统计图能看出世界人口的变化情况;
②2050年非洲人口将达到大约15亿;
③2050年亚洲人口比其他各洲人口的总和还要多;
④从1957年到2050年各洲中北美洲人口增长速度最慢.
其中命题正确的有( )
A.①②
B.①③
C.①④
D.②④
【解析】①从折线统计图能看出世界人口的变化情况,故①正确;②从条形统计图中可得:2050年非洲人口大约将达到18亿,故②错误;③从扇形统计图中能够明显地得到结论:2050年亚洲人口比其他各洲人口的总和还要多,故③正确;④由题中三幅统计图并不能得出从1957年到2050年中哪个洲人口增长速度最慢,故④错误.因此正确的命题有①③.故选B.
【变式1】根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)的柱形图.以下结论不正确的是( )
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量呈增加趋势
【答案】 D
【解析】从2006年,将每年的二氧化硫排放量与前一年作差比较,得到2008年二氧化硫排放量与2007年排放量的差最大,A选项正确;
2007年二氧化硫排放量较2006年降低了很多,B选项正确;
虽然2011年二氧化硫排放量较2010年多一些,但自2006年以来,整体呈递减趋势,C选项正确,D选项错误,故选D.
【例2-2】已知一组数据为第百分位数是(
)
A.
B.
C.
D.
【答案】C
【解析】因为有6位数,所以,所以第百分位数是第三个数6.故选:C
【变式1】数据1,2,3,4,5,6的60%分位数为(
)
A.3
B.3.5
C.3.6
D.4
【答案】D
【解析】由660%=3.6,所以数据1,2,3,4,5,6的60%分位数是第四个数,故选:D
【变式2】“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间内的一个数来表示,该数越接近10表示满意程度越高,现随机抽取6位小区居号,他们的幸福感指数分别为5,6,7,8,9,5,则这组数据的第80百分位数是(
)
A.7
B.7.5
C.8
D.9
【答案】C
【解析】该组数据从小到大排列为:5,5,6,7,8,9,且,故选:C.
【例3-1】在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(单位:m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的众数、中位数与平均数.
【解析】在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.上面表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70.这组数据的平均数是=(1.50×2+1.60×3+…+1.90×1)=≈1.69(m).
故17名运动员成绩的众数、中位数、平均数依次为1.75
m,1.70
m,1.69
m.
【变式1】某学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各1人,则该小组数学成绩的平均数、众数、中位数分别为( )
A.85,85,85
B.87,85,86
C.87,85,85
D.87,85,90
【答案】 C
【解析】平均数为=87,众数为85,中位数为85.
【例3-2】因受新冠疫情的影响,某企业的产品销售面临困难.为了改变现状,该企业欲借助电商和“网红”直播带货扩大销售.受网红效应的影响,产品销售取得了较好的效果.现将该企业一段时间内网上销售的日销售额统计整理后绘制成如下图所示的频率分布直方图:
请根据图中所给数据,求:
(1)实数a的值;
(2)该企业网上销售日销售额的众数和中位数;
(3)该企业在统计时间段内网上销售日销售额的平均数.
【答案】(1)0.012;(2)55万元,57万元;(3)57.4万元.
【解析】(1)由频率分布直方图知:
,解得:;
(2)用频率分布直方图中最高矩形所在区间的中点值作为众数的近似值,得众数为55万元;
因为第一个小矩形的面积为0.08,第二个小矩形的面积为0.12,
第三个小矩形的面积为0.16,,
设第四个小矩形中底边的一部分长为x,则,解得,
所以中位数为万元;
(3)依题意,日销售额的平均值为:
所以该企业在统计时间段内网上销售日销售额的平均数为57.4万元.
【变式1】校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的优秀率(80分及以上为及格)和平均分.
【答案】(1),;(2)优秀率,平均分71分.
【解析】(1)众数是最高小矩形中点的横坐标,所以众数为(分)
前三个小矩形面积为,
∵中位数要平分直方图的面积,
∴.
(2)依题意,80及以上的分数所在的第五、六组,
频率和为
,
所以,抽样学生成绩的合格率是,
利用组中值估算抽样学生的平均分:
,
估计这次考试的平均分是71分.
【变式2】某城市户居民的月平均用水量(单位:吨),以分组的频率分布直方图如图.
(1)求直方图中的值;并估计出月平均用水量的众数.
(2)求月平均用水量的中位数及平均数;
(3)在月平均用水量为,,,的四组用户中,用分层抽样的方法抽取22户居民,则应在这一组的用户中抽取多少户?
(4)在第(3)问抽取的样本中,从这两组中再随机抽取2户,深入调查,则所抽取的两户不是来自同一个组的概率是多少?
【答案】(1)
x=0.075,7;(2)
6.4,5.36;(3)
2;(4).
【解析】(1)根据频率和为1,得2×(0.02+0.095+0.11+0.125+x+0.05+0.025)=1,
解得x=0.075;由图可知,最高矩形的数据组为[6,8),所以众数为;
(2)
[2,6)内的频率之和为
(0.02+0.095+0.11)×2=0.45;
设中位数为y,则0.45+(y?6)×0.125=0.5,
解得y=6.4,∴中位数为6.4;
平均数为
(3)月平均用电量为的用户在四组用户中所占的比例为
,
∴月平均用电量在的用户中应抽取11×=2(户).
(4)月平均用电量在的用户中应抽取11×=1(户),
月平均用电量在的用户设为A、B,
月平均用电量在的用户设为C,
从,这两组中随机抽取2户共有
,3种情况,
其中,抽取的两户不是来自同一个组的有,2种情况,
所以,抽取的两户不是来自同一个组的概率为.
【例4-1】如图所示的四组数据,标准差最小的是(
)
A.
B.
C.
D.
【答案】A
【解析】对A,,
,
对B,,
,
对C,,
,
对D,,
,
所以标准差最小的是A.
故选:A.
【变式1】从甲、乙两种玉米苗中各抽取10株,分别测得它们的株高如下(单位:cm):
甲 25 41 40 37 22 14 19 39 21 42
乙 27 16 44 27 44 16 40 40 16 40
求:(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
【解析】(1)甲=×(25+41+40+37+22+14+19+39+21+42)=30,
同理可计算得乙=31,
∴甲<乙,即乙种玉米苗长得高.
(2)s=×[(25-30)2+(41-30)2+(40-30)2+(37-30)2+(22-30)2+(14-30)2+(19-30)2+(39-30)2+(21-30)2+(42-30)2]=104.2,
同理可计算得s=128.8,
∴s【例4-2】甲、乙两支田径队体检结果为:甲队的体重的平均数为60
kg,方差为200,乙队体重的平均数为70
kg,方差为300,又已知甲、乙两队的队员人数之比为1∶4,那么甲、乙两队全部队员的平均体重和方差分别是什么?
【解析】由题意可知甲=60,甲队队员在所有队员中所占权重为w甲==,
乙=70,乙队队员在所有队员中所占权重为w乙==,
则甲、乙两队全部队员的平均体重为
=w甲甲+w乙乙=×60+×70=68(kg),
甲、乙两队全部队员的体重的方差为
s2=w甲[s+(甲-)2]+w乙[s+(乙-)2]
=[200+(60-68)2]+[300+(70-68)2]=296.
【变式1】某培训机构在假期招收了A,B两个数学补习班,A班10人,B班30人,经过一周的补习后进行了一次测试,在该测试中,A班的平均成绩为130分,方差为115,B班的平均成绩为110分,方差为215.求在这次测试中全体学生的平均成绩和方差.
【解析】依题意A=130,s=115,
B=110,s=215,
∴=×130+×110=115,
∴全体学生的平均成绩为115分.
全体学生成绩的方差为
s2=wA[s+(A-)2]+wB[s+(B-)2]
=×(115+225)+×(215+25)
=85+180=265.
课后练习题
1.为了解学生课外阅读的情况,随机统计了名学生的课外阅读时间,所得数据都在中,其频率分布直方图如图所示.已知在中的频数为100,则的值是(
)
A.500
B.1000
C.10000
D.25000
【答案】B
【解析】由图可得在中的频率为,所以,故选:B.
2.某工厂对一批产品进行了抽样检测.下图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[90,100],样品数据分组为,,,,.已知样本中产品净重小于94克的个数为36,则样本中净重大于或等于92克并且小于98克的产品的个数是(
)
A.
B.
C.
D.
【答案】D
【解析】,,,对应的频率分别为:
设样本容量为
因为净重小于94克的个数为36,所以,解得
则样本中净重大于或等于92克并且小于98克的产品的个数为
故选:D
3.“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的,全世界近人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨):一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使的居民每月的用水不按议价收费,估计的值,并说明理由.
【答案】(1);(2)万;(3)吨.
【解析】(1)由概率统计相关知识,可知各组频率之和的值为
即频率分布直方图各小矩形面积之和为
解得:
(2)由图可知,不低于吨人数所占百分比为
全市月均用水量不低于吨的人数为:(万)
(3)由(2)可知,月均用水量小于吨的居民人数所占百分比为:
即的居民月均用水量小于吨,同理,的居民月均用水量小于吨
故
假设月均用水量平均分布,则(吨)
4.随机观测生产某种零件的某工厂名工人的日加工零件数(单位:件),获得数据如下:、、、、、、、、、、、、、、、、、、、、、、、、,根据上述数据得到样本的频率分布表如下:
分组
频数
频率
(1)确定样本频率分布表中、、和的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取人,至少有人的日加工零件数落在区间的概率.
【答案】(1),,
,;(2)详见解析;(3).
【解析】(1)由题意知,,
,;
(2)样本频率分布直方图为:
(3)根据样本频率分布直方图,每人的日加工零件数落在区间的概率,
设所取的人中,日加工零件数落在区间的人数为,则,
,
所以人中,至少有人的日加工零件数落在区间的概率约为.
5.数据10,9,8,7,6,5,4,3,2,1的25%分位数、80%分位数分别是_______;
【答案】3;8.5
【解析】将数据10,9,8,7,6,5,4,3,2,1从小到大排序得:1,2,3,4,5,6,7,8,9,10,
当时,,分位数为3.
当时,,分位数为.故答案为:3;8.5.
6.2020年宿州市某中学参加高中数学建模(应用)能力测试,高一年级有60人,高二年级有40人.高一的平均成绩为70分,高二的平均成绩为80分,则参加测试的100名学生的平均成绩为(
)
A.72分
B.73分
C.74分
D.75分
【答案】C
【解析】由题意可得,参加测试的100名学生的平均成绩为.故选:C.
7.根据气象学上的标准,连续天的日平均气温低于即为入冬.现有甲、乙、丙、丁四地连续天的日平均温度的记录数据(记录数据都是正整数):
①甲地:个数据的中位数为,众数为;
②乙地:个数据的平均数为,极差为;
③丙地:个数据的平均数为,中位数为;
④丁地:个数据的平均数为,方差小于.
则肯定进入冬季的地区是(
)
A.甲地
B.乙地
C.丙地
D.丁地
【答案】D
【解析】①甲地:个数据的中位数为,众数为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以甲地不一定入冬,故A错;
②乙地:个数据的平均数为,极差为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以乙地不一定入冬,故B错;
③丙地:个数据的平均数为,中位数为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以丙地不一定入冬,故C错;
④丁地:个数据的平均数为,方差小于.如有数据大于等于,则方差必大于等于,不满足题意,因此丁地这续天的日平均气温都低于,所以丁地一定入冬,故D正确;
故选:D.
8.某地教育部门对某学校学生的阅读素养进行检测,在该校随机抽取了名学生进行检测,实行百分制,现将所得的成绩按照,分成6组,并根据所得数据作出了如下所示的频数与频率的统计表和频率分布直方图.
分组
频数
频率
25
0.30
10
0.10
合计
1
(1)求出表中及图中的值;
(2)估计该校学生阅读素养的成绩中位数以及平均数.
【答案】(1);(2)中位数是,平均数是68.5.
【解析】(1)由频率统计表可知:,
由频率分布直方图可知:,解得
(2)∵前两组的频率和为,前三组的频率和为
∴中位数在内,设中位数为,则,解得,即中位数为.
平均数为
∴估计该校学生阅读素养的成绩中位数是,平均数是68.5.
9.(多选)国家为了实现经济“双循环”大战略,对东部和西部地区的多个县市的某一类经济指标进行调查,得出东部,西部两组数据的茎叶图如图所示,则下列结论正确的是(
)
A.西部的平均数为13.3
B.东部的极差小于西部的极差
C.东部的30%分位数是11.6
D.东部的众数比西部的众数小
【答案】ACD
【解析】对于A:即西部的平均数为13.3,故A正确;
对于B:东部的最大值为,最小值为,极差为;西部的最大值为,最小值为,极差为;故B错误;
对于C:东部共13个数据,,即从小到大的第4个数为东部的30%分位数,所以东部的30%分位数是11.6,故C正确;
对于D:东部的众数为,西部的众数为和均大于,故D正确;
故选:ACD
10.为庆祝国庆节,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名,将其成绩(成绩均为整数)分成[40,50),[50,60),…,[90,100]六组,并画出如图所示的部分频率分布直方图,观察图形,回答下列问题:
(1)求第四组的频率,并补全这个频率分布直方图;
(2)请根据频率分布直方图,估计样本的中位数和方差.(每组数据以区间的中点值为代表).
【答案】(1)第四组的频率为;作图见解析;(2);194.
【解析】因为各组的频率和等于1,所以第四组的频率为
.
补全的频率分布直方图如图所示.
(2)前三组的频率之和为:
前四组的频率之和为:
设中位数为,则应有
又,即样本的中位数为
抽取学生的平均数约为所以,样本的方差为:
.
【知识点一】频率分布直方图
作频率分布直方图的步骤
1.求极差:极差为一组数据中最大值与最小值的差.
2.决定组距与组数
将数据分组时,一般取等长组距,并且组距应力求“取整”,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.
3.将数据分组
4.列频率分布表
各小组的频率=.
5.画频率分布直方图
纵轴表示,实际上就是频率分布直方图中各小长方形的高度,小长方形的面积=组距×=频率.
【知识点二】常见统计图表的特点与区别
扇形图主要用于直观描述各类数据占总数的比例,条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率,条形图适用于描述离散型数据,直方图适用于描述连续型数据.折线图主要用于描述数据随时间的变化趋势.
【知识点三】百分位数
1.百分位数定义:一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
2.常用的百分位数
(1)四分位数:第25百分位数,第50百分位数,第75百分位数.
(2)其它常用的百分位数:第1百分位数,第5百分位数,第95百分位数,第99百分位数.
3.计算一组n个数据的第p百分位数的一般步骤如下:
第1步,按从小到大排列原始数据;
第2步,计算i=n×p%;
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
【知识点四】众数、中位数、平均数
1.众数:一组数据中出现次数最多的数.
2.中位数:把一组数据按从小到大(或从大到小)的顺序排列,处在中间位置的数(或中间两个数的平均数)叫做这组数据的中位数.
3.平均数:如果n个数x1,x2,…,xn,那么=(x1+x2+…+xn)叫做这n个数的平均数.
【知识点五】总体集中趋势的估计
1.平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势.
2.一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
【知识点六】频率分布直方图中平均数、中位数、众数的求法
1.样本平均数:可以用每个小矩形底边中点的横坐标与小矩形面积的乘积之和近似代替.
2.在频率分布直方图中,中位数左边和右边的直方图的面积应相等.
3.将最高小矩形所在的区间中点作为众数的估计值.
【知识点七】方差、标准差
1.假设一组数据为x1,x2,…xn,则这组数据的平均数=,方差为s2=(xi-)2,标准差
2.如果总体中所有个体的变量值分别为Y1,Y2,…,YN,总体平均数为,则称S2=(Yi-)2为总体方差,S=为总体标准差.
如果总体的N个变量值中,不同的值共有k(k≤N)个,不妨记为Y1,Y2,…,Yk,其中Yi出现的频数为fi(i=1,2,…,k),则总体方差为S2=(Yi-)2.
3.如果一个样本中个体的变量值分别为y1,y2,…,yn,样本平均数为,则称s2=(yi-)2为样本方差,s=为样本标准差.
4.标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.
【例1-1】一个容量为100的样本,其数据的分组与各组的频数如下:
分组
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
[60,70]
频数
12
13
24
15
16
13
7
则样本数据落在[10,40)上的频率为( )
A.0.13
B.0.39
C.0.52
D.0.64
【变式1】容量为100的某个样本,数据拆分为10组,若前七组频率之和为0.79,而剩下的三组的频率依次相差0.05,则剩下的三组中频率最大的一组频率为________.
【例1-2】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
用户用水量频数直方图
用户用水量扇形统计图
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格.
【变式1】某市2020年4月1日~4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,
77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,空间质量为良;在101~150之间时,空间质量为轻微污染;在151~200之间时,空间质量为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
【例1-3】为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50kW·h至350kW·h之间,进行适当分组后,画出频率分布直方图如图所示.
(I)求a的值;
(Ⅱ)求被调查用户中,用电量大于250kW·h的户数;
(III)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,希望使80%的居民缴费在第一档(费用最低),请给出第一档用电标准(单位:kW·h)的建议,并简要说明理由.
【变式1】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的比例;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论).
【例2-1】(1)给出如图所示的三幅统计图及四个命题:
①从折线统计图能看出世界人口的变化情况;
②2050年非洲人口将达到大约15亿;
③2050年亚洲人口比其他各洲人口的总和还要多;
④从1957年到2050年各洲中北美洲人口增长速度最慢.
其中命题正确的有( )
A.①②
B.①③
C.①④
D.②④
【变式1】根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)的柱形图.以下结论不正确的是( )
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量呈增加趋势
【例2-2】已知一组数据为第百分位数是(
)
A.
B.
C.
D.
【变式1】数据1,2,3,4,5,6的60%分位数为(
)
A.3
B.3.5
C.3.6
D.4
【变式2】“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间内的一个数来表示,该数越接近10表示满意程度越高,现随机抽取6位小区居号,他们的幸福感指数分别为5,6,7,8,9,5,则这组数据的第80百分位数是(
)
A.7
B.7.5
C.8
D.9
【例3-1】在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(单位:m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的众数、中位数与平均数.
【变式1】某学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各1人,则该小组数学成绩的平均数、众数、中位数分别为( )
A.85,85,85
B.87,85,86
C.87,85,85
D.87,85,90
【例3-2】因受新冠疫情的影响,某企业的产品销售面临困难.为了改变现状,该企业欲借助电商和“网红”直播带货扩大销售.受网红效应的影响,产品销售取得了较好的效果.现将该企业一段时间内网上销售的日销售额统计整理后绘制成如下图所示的频率分布直方图:
请根据图中所给数据,求:
(1)实数a的值;
(2)该企业网上销售日销售额的众数和中位数;
(3)该企业在统计时间段内网上销售日销售额的平均数.
【变式1】校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的优秀率(80分及以上为及格)和平均分.
【变式2】某城市户居民的月平均用水量(单位:吨),以分组的频率分布直方图如图.
(1)求直方图中的值;并估计出月平均用水量的众数.
(2)求月平均用水量的中位数及平均数;
(3)在月平均用水量为,,,的四组用户中,用分层抽样的方法抽取22户居民,则应在这一组的用户中抽取多少户?
(4)在第(3)问抽取的样本中,从这两组中再随机抽取2户,深入调查,则所抽取的两户不是来自同一个组的概率是多少?
【例4-1】如图所示的四组数据,标准差最小的是(
)
A.
B.
C.
D.
【变式1】从甲、乙两种玉米苗中各抽取10株,分别测得它们的株高如下(单位:cm):
甲 25 41 40 37 22 14 19 39 21 42
乙 27 16 44 27 44 16 40 40 16 40
求:(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
【例4-2】甲、乙两支田径队体检结果为:甲队的体重的平均数为60
kg,方差为200,乙队体重的平均数为70
kg,方差为300,又已知甲、乙两队的队员人数之比为1∶4,那么甲、乙两队全部队员的平均体重和方差分别是什么?
【变式1】某培训机构在假期招收了A,B两个数学补习班,A班10人,B班30人,经过一周的补习后进行了一次测试,在该测试中,A班的平均成绩为130分,方差为115,B班的平均成绩为110分,方差为215.求在这次测试中全体学生的平均成绩和方差.
课后练习题
1.为了解学生课外阅读的情况,随机统计了名学生的课外阅读时间,所得数据都在中,其频率分布直方图如图所示.已知在中的频数为100,则的值是(
)
A.500
B.1000
C.10000
D.25000
2.某工厂对一批产品进行了抽样检测.下图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[90,100],样品数据分组为,,,,.已知样本中产品净重小于94克的个数为36,则样本中净重大于或等于92克并且小于98克的产品的个数是(
)
A.
B.
C.
D.
3.“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的,全世界近人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨):一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使的居民每月的用水不按议价收费,估计的值,并说明理由.
4.随机观测生产某种零件的某工厂名工人的日加工零件数(单位:件),获得数据如下:、、、、、、、、、、、、、、、、、、、、、、、、,根据上述数据得到样本的频率分布表如下:
分组
频数
频率
(1)确定样本频率分布表中、、和的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取人,至少有人的日加工零件数落在区间的概率.
5.数据10,9,8,7,6,5,4,3,2,1的25%分位数、80%分位数分别是_______;
6.2020年宿州市某中学参加高中数学建模(应用)能力测试,高一年级有60人,高二年级有40人.高一的平均成绩为70分,高二的平均成绩为80分,则参加测试的100名学生的平均成绩为(
)
A.72分
B.73分
C.74分
D.75分
7.根据气象学上的标准,连续天的日平均气温低于即为入冬.现有甲、乙、丙、丁四地连续天的日平均温度的记录数据(记录数据都是正整数):
①甲地:个数据的中位数为,众数为;
②乙地:个数据的平均数为,极差为;
③丙地:个数据的平均数为,中位数为;
④丁地:个数据的平均数为,方差小于.
则肯定进入冬季的地区是(
)
A.甲地
B.乙地
C.丙地
D.丁地
8.某地教育部门对某学校学生的阅读素养进行检测,在该校随机抽取了名学生进行检测,实行百分制,现将所得的成绩按照,分成6组,并根据所得数据作出了如下所示的频数与频率的统计表和频率分布直方图.
分组
频数
频率
25
0.30
10
0.10
合计
1
(1)求出表中及图中的值;
(2)估计该校学生阅读素养的成绩中位数以及平均数.
9.(多选)国家为了实现经济“双循环”大战略,对东部和西部地区的多个县市的某一类经济指标进行调查,得出东部,西部两组数据的茎叶图如图所示,则下列结论正确的是(
)
A.西部的平均数为13.3
B.东部的极差小于西部的极差
C.东部的30%分位数是11.6
D.东部的众数比西部的众数小
10.为庆祝国庆节,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名,将其成绩(成绩均为整数)分成[40,50),[50,60),…,[90,100]六组,并画出如图所示的部分频率分布直方图,观察图形,回答下列问题:
(1)求第四组的频率,并补全这个频率分布直方图;
(2)请根据频率分布直方图,估计样本的中位数和方差.(每组数据以区间的中点值为代表).
9.2 用样本估计总体
【知识点一】频率分布直方图
作频率分布直方图的步骤
1.求极差:极差为一组数据中最大值与最小值的差.
2.决定组距与组数
将数据分组时,一般取等长组距,并且组距应力求“取整”,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.
3.将数据分组
4.列频率分布表
各小组的频率=.
5.画频率分布直方图
纵轴表示,实际上就是频率分布直方图中各小长方形的高度,小长方形的面积=组距×=频率.
【知识点二】常见统计图表的特点与区别
扇形图主要用于直观描述各类数据占总数的比例,条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率,条形图适用于描述离散型数据,直方图适用于描述连续型数据.折线图主要用于描述数据随时间的变化趋势.
【知识点三】百分位数
1.百分位数定义:一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
2.常用的百分位数
(1)四分位数:第25百分位数,第50百分位数,第75百分位数.
(2)其它常用的百分位数:第1百分位数,第5百分位数,第95百分位数,第99百分位数.
3.计算一组n个数据的第p百分位数的一般步骤如下:
第1步,按从小到大排列原始数据;
第2步,计算i=n×p%;
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
【知识点四】众数、中位数、平均数
1.众数:一组数据中出现次数最多的数.
2.中位数:把一组数据按从小到大(或从大到小)的顺序排列,处在中间位置的数(或中间两个数的平均数)叫做这组数据的中位数.
3.平均数:如果n个数x1,x2,…,xn,那么=(x1+x2+…+xn)叫做这n个数的平均数.
【知识点五】总体集中趋势的估计
1.平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势.
2.一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
【知识点六】频率分布直方图中平均数、中位数、众数的求法
1.样本平均数:可以用每个小矩形底边中点的横坐标与小矩形面积的乘积之和近似代替.
2.在频率分布直方图中,中位数左边和右边的直方图的面积应相等.
3.将最高小矩形所在的区间中点作为众数的估计值.
【知识点七】方差、标准差
1.假设一组数据为x1,x2,…xn,则这组数据的平均数=,方差为s2=(xi-)2,标准差
2.如果总体中所有个体的变量值分别为Y1,Y2,…,YN,总体平均数为,则称S2=(Yi-)2为总体方差,S=为总体标准差.
如果总体的N个变量值中,不同的值共有k(k≤N)个,不妨记为Y1,Y2,…,Yk,其中Yi出现的频数为fi(i=1,2,…,k),则总体方差为S2=(Yi-)2.
3.如果一个样本中个体的变量值分别为y1,y2,…,yn,样本平均数为,则称s2=(yi-)2为样本方差,s=为样本标准差.
4.标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.
【例1-1】一个容量为100的样本,其数据的分组与各组的频数如下:
分组
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
[60,70]
频数
12
13
24
15
16
13
7
则样本数据落在[10,40)上的频率为( )
A.0.13
B.0.39
C.0.52
D.0.64
【答案】C
【解析】由题意可知样本数据落在[10,40)的频数为13+24+15=52,所以频率为=0.52.故选C.
【变式1】容量为100的某个样本,数据拆分为10组,若前七组频率之和为0.79,而剩下的三组的频率依次相差0.05,则剩下的三组中频率最大的一组频率为________.
【答案】0.12
【解析】设剩下的三组中频率最大的一组的频率为x,则另两组的频率分别为x-0.05,x-0.1,而由频率和为1得0.79+(x-0.05)+(x-0.1)+x=1,解得x=0.12.
【例1-2】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
用户用水量频数直方图
用户用水量扇形统计图
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格.
【答案】(1)答案见解析;(2)答案见解析,79.2°;(3)4.08万户.
【解析】(1);
(2)用水15~20吨的户数为100-10-36-24-8=22(户),
“15~20吨”部分的圆心角的度数为
(3)(万户)
所以该地区6万用户中约有4.08万户的用水全部享受基本价格.
【变式1】某市2020年4月1日~4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,
77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,空间质量为良;在101~150之间时,空间质量为轻微污染;在151~200之间时,空间质量为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
【答案】(1)频率分布表见解析;(2)频率分布直方图见解析;(3)该市空气质量有待进一步改善.
【解析】(1)频率分布表
分组
频数
频率
分组
频数
频率
[41,51)
2
[81,91)
10
[51,61)
1
[91,101)
5
[61,71)
4
[101,111)
2
[71,81)
6
(2)频率分布直方图
(3)答对下述两条中的一条即可:
①该市一个月中空气污染指数有2天处于优的水平,占当月天数的;
有26天处于良的水平,占当月天数的;
处于优或良的天数共有28天,占当月天数的.说明该市空气质量基本良好.
②轻微污染有2天,占当月天数的.污染指数在80以上的接近轻微污染的天数有
15天,加上处于轻微污染的天数,共有17天,占当月天数的,超过50%.
说明该市空气质量有待进一步改善.
【例1-3】为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50kW·h至350kW·h之间,进行适当分组后,画出频率分布直方图如图所示.
(I)求a的值;
(Ⅱ)求被调查用户中,用电量大于250kW·h的户数;
(III)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,希望使80%的居民缴费在第一档(费用最低),请给出第一档用电标准(单位:kW·h)的建议,并简要说明理由.
【答案】(I);(Ⅱ);(III)
kW·h.
【解析】(1)因为,所以;
(2)根据频率分布直方图可知:“用电量大于250kW·h”的频率为,
所以用电量大于250kW·h的户数为:,
故用电量大于250kW·h有户;
(3)因为前三组的频率和为:,
前四组的频率之和为,
所以频率为时对应的数据在第四组,
所以第一档用电标准为:kW·h.
故第一档用电标准为
kW·h.
【变式1】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的比例;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论).
【解析】(1)根据频数分布表知,100名学生中一周课外阅读时间不少于12小时的学生共有6+2+2=10(名),
所以样本中的学生一周课外阅读时间少于12小时的频率是1-=0.9.
故从该校随机选取一名学生,估计其该周课外阅读时间少于12小时的比例为0.9.
(2)课外阅读时间落在[4,6)组内的有17人,频率为0.17,所以a===0.085.
课外阅读时间落在[8,10)组内的有25人,频率为0.25,
所以b===0.125.
(3)样本中的100名学生该周课外阅读时间的平均数在第4组.
【例2-1】(1)给出如图所示的三幅统计图及四个命题:
①从折线统计图能看出世界人口的变化情况;
②2050年非洲人口将达到大约15亿;
③2050年亚洲人口比其他各洲人口的总和还要多;
④从1957年到2050年各洲中北美洲人口增长速度最慢.
其中命题正确的有( )
A.①②
B.①③
C.①④
D.②④
【解析】①从折线统计图能看出世界人口的变化情况,故①正确;②从条形统计图中可得:2050年非洲人口大约将达到18亿,故②错误;③从扇形统计图中能够明显地得到结论:2050年亚洲人口比其他各洲人口的总和还要多,故③正确;④由题中三幅统计图并不能得出从1957年到2050年中哪个洲人口增长速度最慢,故④错误.因此正确的命题有①③.故选B.
【变式1】根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)的柱形图.以下结论不正确的是( )
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量呈增加趋势
【答案】 D
【解析】从2006年,将每年的二氧化硫排放量与前一年作差比较,得到2008年二氧化硫排放量与2007年排放量的差最大,A选项正确;
2007年二氧化硫排放量较2006年降低了很多,B选项正确;
虽然2011年二氧化硫排放量较2010年多一些,但自2006年以来,整体呈递减趋势,C选项正确,D选项错误,故选D.
【例2-2】已知一组数据为第百分位数是(
)
A.
B.
C.
D.
【答案】C
【解析】因为有6位数,所以,所以第百分位数是第三个数6.故选:C
【变式1】数据1,2,3,4,5,6的60%分位数为(
)
A.3
B.3.5
C.3.6
D.4
【答案】D
【解析】由660%=3.6,所以数据1,2,3,4,5,6的60%分位数是第四个数,故选:D
【变式2】“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间内的一个数来表示,该数越接近10表示满意程度越高,现随机抽取6位小区居号,他们的幸福感指数分别为5,6,7,8,9,5,则这组数据的第80百分位数是(
)
A.7
B.7.5
C.8
D.9
【答案】C
【解析】该组数据从小到大排列为:5,5,6,7,8,9,且,故选:C.
【例3-1】在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(单位:m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的众数、中位数与平均数.
【解析】在17个数据中,1.75出现了4次,出现的次数最多,即这组数据的众数是1.75.上面表里的17个数据可看成是按从小到大的顺序排列的,其中第9个数据1.70是最中间的一个数据,即这组数据的中位数是1.70.这组数据的平均数是=(1.50×2+1.60×3+…+1.90×1)=≈1.69(m).
故17名运动员成绩的众数、中位数、平均数依次为1.75
m,1.70
m,1.69
m.
【变式1】某学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各1人,则该小组数学成绩的平均数、众数、中位数分别为( )
A.85,85,85
B.87,85,86
C.87,85,85
D.87,85,90
【答案】 C
【解析】平均数为=87,众数为85,中位数为85.
【例3-2】因受新冠疫情的影响,某企业的产品销售面临困难.为了改变现状,该企业欲借助电商和“网红”直播带货扩大销售.受网红效应的影响,产品销售取得了较好的效果.现将该企业一段时间内网上销售的日销售额统计整理后绘制成如下图所示的频率分布直方图:
请根据图中所给数据,求:
(1)实数a的值;
(2)该企业网上销售日销售额的众数和中位数;
(3)该企业在统计时间段内网上销售日销售额的平均数.
【答案】(1)0.012;(2)55万元,57万元;(3)57.4万元.
【解析】(1)由频率分布直方图知:
,解得:;
(2)用频率分布直方图中最高矩形所在区间的中点值作为众数的近似值,得众数为55万元;
因为第一个小矩形的面积为0.08,第二个小矩形的面积为0.12,
第三个小矩形的面积为0.16,,
设第四个小矩形中底边的一部分长为x,则,解得,
所以中位数为万元;
(3)依题意,日销售额的平均值为:
所以该企业在统计时间段内网上销售日销售额的平均数为57.4万元.
【变式1】校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的优秀率(80分及以上为及格)和平均分.
【答案】(1),;(2)优秀率,平均分71分.
【解析】(1)众数是最高小矩形中点的横坐标,所以众数为(分)
前三个小矩形面积为,
∵中位数要平分直方图的面积,
∴.
(2)依题意,80及以上的分数所在的第五、六组,
频率和为
,
所以,抽样学生成绩的合格率是,
利用组中值估算抽样学生的平均分:
,
估计这次考试的平均分是71分.
【变式2】某城市户居民的月平均用水量(单位:吨),以分组的频率分布直方图如图.
(1)求直方图中的值;并估计出月平均用水量的众数.
(2)求月平均用水量的中位数及平均数;
(3)在月平均用水量为,,,的四组用户中,用分层抽样的方法抽取22户居民,则应在这一组的用户中抽取多少户?
(4)在第(3)问抽取的样本中,从这两组中再随机抽取2户,深入调查,则所抽取的两户不是来自同一个组的概率是多少?
【答案】(1)
x=0.075,7;(2)
6.4,5.36;(3)
2;(4).
【解析】(1)根据频率和为1,得2×(0.02+0.095+0.11+0.125+x+0.05+0.025)=1,
解得x=0.075;由图可知,最高矩形的数据组为[6,8),所以众数为;
(2)
[2,6)内的频率之和为
(0.02+0.095+0.11)×2=0.45;
设中位数为y,则0.45+(y?6)×0.125=0.5,
解得y=6.4,∴中位数为6.4;
平均数为
(3)月平均用电量为的用户在四组用户中所占的比例为
,
∴月平均用电量在的用户中应抽取11×=2(户).
(4)月平均用电量在的用户中应抽取11×=1(户),
月平均用电量在的用户设为A、B,
月平均用电量在的用户设为C,
从,这两组中随机抽取2户共有
,3种情况,
其中,抽取的两户不是来自同一个组的有,2种情况,
所以,抽取的两户不是来自同一个组的概率为.
【例4-1】如图所示的四组数据,标准差最小的是(
)
A.
B.
C.
D.
【答案】A
【解析】对A,,
,
对B,,
,
对C,,
,
对D,,
,
所以标准差最小的是A.
故选:A.
【变式1】从甲、乙两种玉米苗中各抽取10株,分别测得它们的株高如下(单位:cm):
甲 25 41 40 37 22 14 19 39 21 42
乙 27 16 44 27 44 16 40 40 16 40
求:(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
【解析】(1)甲=×(25+41+40+37+22+14+19+39+21+42)=30,
同理可计算得乙=31,
∴甲<乙,即乙种玉米苗长得高.
(2)s=×[(25-30)2+(41-30)2+(40-30)2+(37-30)2+(22-30)2+(14-30)2+(19-30)2+(39-30)2+(21-30)2+(42-30)2]=104.2,
同理可计算得s=128.8,
∴s
kg,方差为200,乙队体重的平均数为70
kg,方差为300,又已知甲、乙两队的队员人数之比为1∶4,那么甲、乙两队全部队员的平均体重和方差分别是什么?
【解析】由题意可知甲=60,甲队队员在所有队员中所占权重为w甲==,
乙=70,乙队队员在所有队员中所占权重为w乙==,
则甲、乙两队全部队员的平均体重为
=w甲甲+w乙乙=×60+×70=68(kg),
甲、乙两队全部队员的体重的方差为
s2=w甲[s+(甲-)2]+w乙[s+(乙-)2]
=[200+(60-68)2]+[300+(70-68)2]=296.
【变式1】某培训机构在假期招收了A,B两个数学补习班,A班10人,B班30人,经过一周的补习后进行了一次测试,在该测试中,A班的平均成绩为130分,方差为115,B班的平均成绩为110分,方差为215.求在这次测试中全体学生的平均成绩和方差.
【解析】依题意A=130,s=115,
B=110,s=215,
∴=×130+×110=115,
∴全体学生的平均成绩为115分.
全体学生成绩的方差为
s2=wA[s+(A-)2]+wB[s+(B-)2]
=×(115+225)+×(215+25)
=85+180=265.
课后练习题
1.为了解学生课外阅读的情况,随机统计了名学生的课外阅读时间,所得数据都在中,其频率分布直方图如图所示.已知在中的频数为100,则的值是(
)
A.500
B.1000
C.10000
D.25000
【答案】B
【解析】由图可得在中的频率为,所以,故选:B.
2.某工厂对一批产品进行了抽样检测.下图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[90,100],样品数据分组为,,,,.已知样本中产品净重小于94克的个数为36,则样本中净重大于或等于92克并且小于98克的产品的个数是(
)
A.
B.
C.
D.
【答案】D
【解析】,,,对应的频率分别为:
设样本容量为
因为净重小于94克的个数为36,所以,解得
则样本中净重大于或等于92克并且小于98克的产品的个数为
故选:D
3.“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的,全世界近人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨):一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使的居民每月的用水不按议价收费,估计的值,并说明理由.
【答案】(1);(2)万;(3)吨.
【解析】(1)由概率统计相关知识,可知各组频率之和的值为
即频率分布直方图各小矩形面积之和为
解得:
(2)由图可知,不低于吨人数所占百分比为
全市月均用水量不低于吨的人数为:(万)
(3)由(2)可知,月均用水量小于吨的居民人数所占百分比为:
即的居民月均用水量小于吨,同理,的居民月均用水量小于吨
故
假设月均用水量平均分布,则(吨)
4.随机观测生产某种零件的某工厂名工人的日加工零件数(单位:件),获得数据如下:、、、、、、、、、、、、、、、、、、、、、、、、,根据上述数据得到样本的频率分布表如下:
分组
频数
频率
(1)确定样本频率分布表中、、和的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取人,至少有人的日加工零件数落在区间的概率.
【答案】(1),,
,;(2)详见解析;(3).
【解析】(1)由题意知,,
,;
(2)样本频率分布直方图为:
(3)根据样本频率分布直方图,每人的日加工零件数落在区间的概率,
设所取的人中,日加工零件数落在区间的人数为,则,
,
所以人中,至少有人的日加工零件数落在区间的概率约为.
5.数据10,9,8,7,6,5,4,3,2,1的25%分位数、80%分位数分别是_______;
【答案】3;8.5
【解析】将数据10,9,8,7,6,5,4,3,2,1从小到大排序得:1,2,3,4,5,6,7,8,9,10,
当时,,分位数为3.
当时,,分位数为.故答案为:3;8.5.
6.2020年宿州市某中学参加高中数学建模(应用)能力测试,高一年级有60人,高二年级有40人.高一的平均成绩为70分,高二的平均成绩为80分,则参加测试的100名学生的平均成绩为(
)
A.72分
B.73分
C.74分
D.75分
【答案】C
【解析】由题意可得,参加测试的100名学生的平均成绩为.故选:C.
7.根据气象学上的标准,连续天的日平均气温低于即为入冬.现有甲、乙、丙、丁四地连续天的日平均温度的记录数据(记录数据都是正整数):
①甲地:个数据的中位数为,众数为;
②乙地:个数据的平均数为,极差为;
③丙地:个数据的平均数为,中位数为;
④丁地:个数据的平均数为,方差小于.
则肯定进入冬季的地区是(
)
A.甲地
B.乙地
C.丙地
D.丁地
【答案】D
【解析】①甲地:个数据的中位数为,众数为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以甲地不一定入冬,故A错;
②乙地:个数据的平均数为,极差为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以乙地不一定入冬,故B错;
③丙地:个数据的平均数为,中位数为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以丙地不一定入冬,故C错;
④丁地:个数据的平均数为,方差小于.如有数据大于等于,则方差必大于等于,不满足题意,因此丁地这续天的日平均气温都低于,所以丁地一定入冬,故D正确;
故选:D.
8.某地教育部门对某学校学生的阅读素养进行检测,在该校随机抽取了名学生进行检测,实行百分制,现将所得的成绩按照,分成6组,并根据所得数据作出了如下所示的频数与频率的统计表和频率分布直方图.
分组
频数
频率
25
0.30
10
0.10
合计
1
(1)求出表中及图中的值;
(2)估计该校学生阅读素养的成绩中位数以及平均数.
【答案】(1);(2)中位数是,平均数是68.5.
【解析】(1)由频率统计表可知:,
由频率分布直方图可知:,解得
(2)∵前两组的频率和为,前三组的频率和为
∴中位数在内,设中位数为,则,解得,即中位数为.
平均数为
∴估计该校学生阅读素养的成绩中位数是,平均数是68.5.
9.(多选)国家为了实现经济“双循环”大战略,对东部和西部地区的多个县市的某一类经济指标进行调查,得出东部,西部两组数据的茎叶图如图所示,则下列结论正确的是(
)
A.西部的平均数为13.3
B.东部的极差小于西部的极差
C.东部的30%分位数是11.6
D.东部的众数比西部的众数小
【答案】ACD
【解析】对于A:即西部的平均数为13.3,故A正确;
对于B:东部的最大值为,最小值为,极差为;西部的最大值为,最小值为,极差为;故B错误;
对于C:东部共13个数据,,即从小到大的第4个数为东部的30%分位数,所以东部的30%分位数是11.6,故C正确;
对于D:东部的众数为,西部的众数为和均大于,故D正确;
故选:ACD
10.为庆祝国庆节,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名,将其成绩(成绩均为整数)分成[40,50),[50,60),…,[90,100]六组,并画出如图所示的部分频率分布直方图,观察图形,回答下列问题:
(1)求第四组的频率,并补全这个频率分布直方图;
(2)请根据频率分布直方图,估计样本的中位数和方差.(每组数据以区间的中点值为代表).
【答案】(1)第四组的频率为;作图见解析;(2);194.
【解析】因为各组的频率和等于1,所以第四组的频率为
.
补全的频率分布直方图如图所示.
(2)前三组的频率之和为:
前四组的频率之和为:
设中位数为,则应有
又,即样本的中位数为
抽取学生的平均数约为所以,样本的方差为:
.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
