2.4单摆 2.5实验:用单摆测重力加速度 课件 (共30张PPT)
文档属性
| 名称 | 2.4单摆 2.5实验:用单摆测重力加速度 课件 (共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 691.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-06 14:07:36 | ||
图片预览




文档简介
(共30张PPT)
2.4
单
摆
复
习
提
问
1.机械振动
2.简谐运动
物体(或物体的一部分)在某一中心位置两侧所做的往复运动叫做机械振动。
物体在跟位移大小成正比、并且总是指向平衡位置的回复力作用下的振动,叫做简谐运动。
3.简谐运动的条件
F
=-
kX
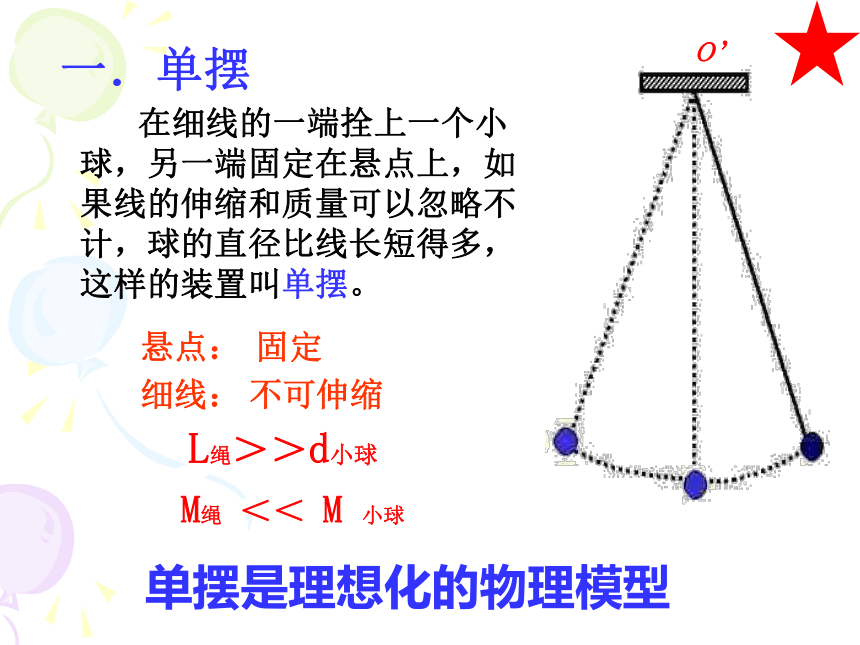
一.单摆
在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多,这样的装置叫单摆。
悬点:
不可伸缩
固定
细线:
单摆是理想化的物理模型
L绳>>d小球
M绳
<<
M
小球
O’
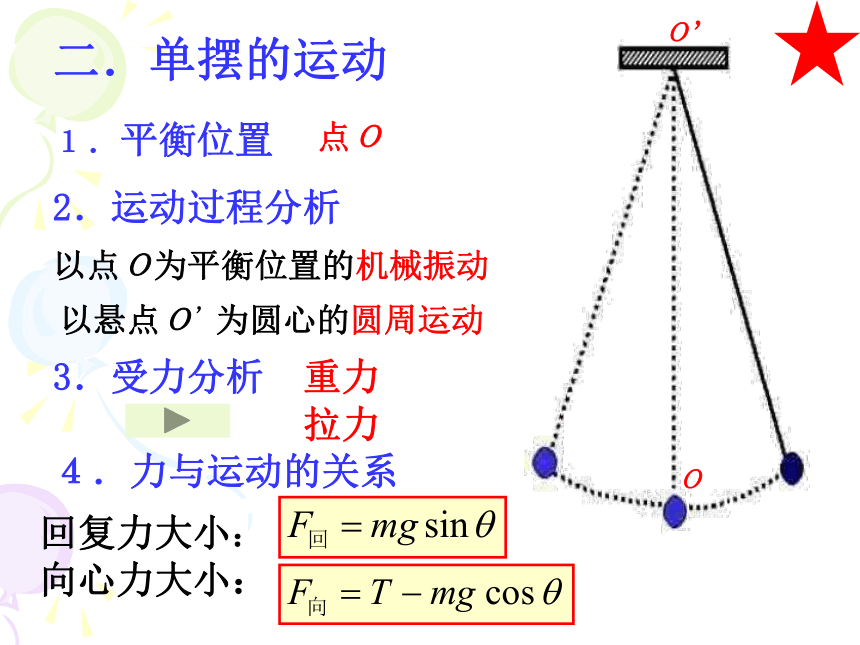
二.单摆的运动
1.平衡位置
3.受力分析
重力
拉力
2.运动过程分析
以悬点O’为圆心的圆周运动
以点O为平衡位置的机械振动
4.力与运动的关系
回复力大小:
向心力大小:
点O
O’
O
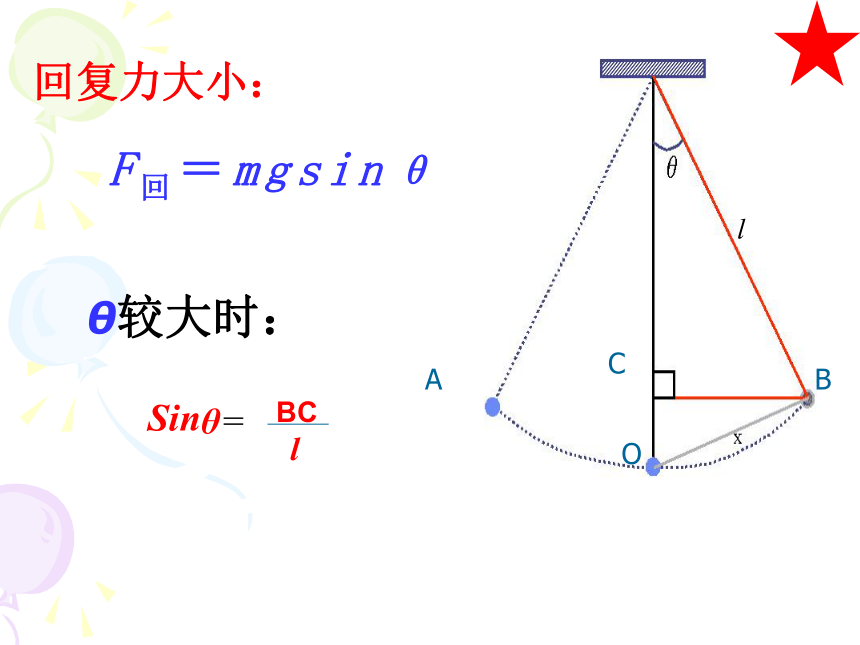
回复力大小:
F回=mgsinθ
A
B
O
C
l
θ较大时:
Sinθ=
l
BC
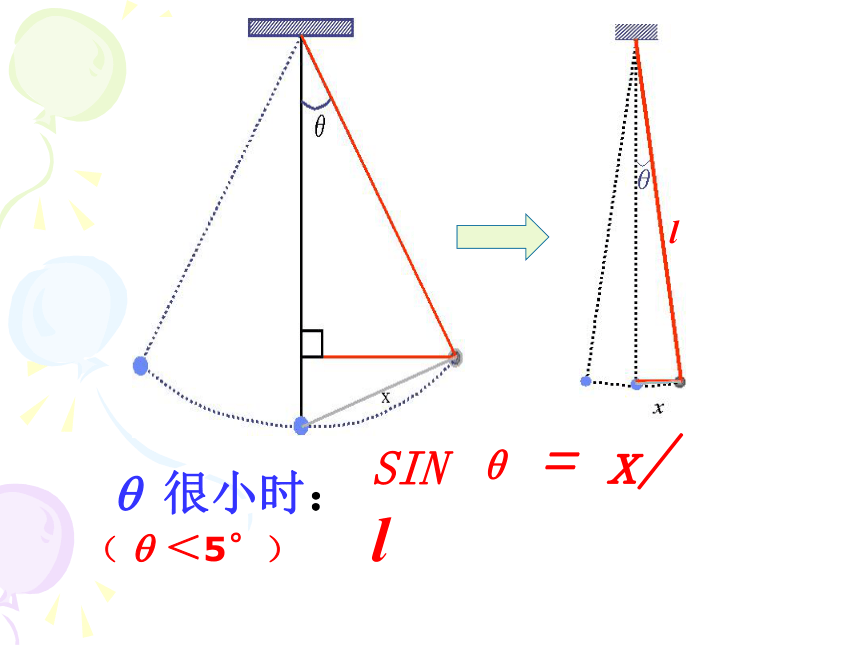
?
很小时:
SIN
θ
=
x/
l
l
(
?
<5°)
在摆角很小的情况下,单摆所受回复力跟位移成正比且方向相反,单摆做简谐运动.
?
x
(?<100)
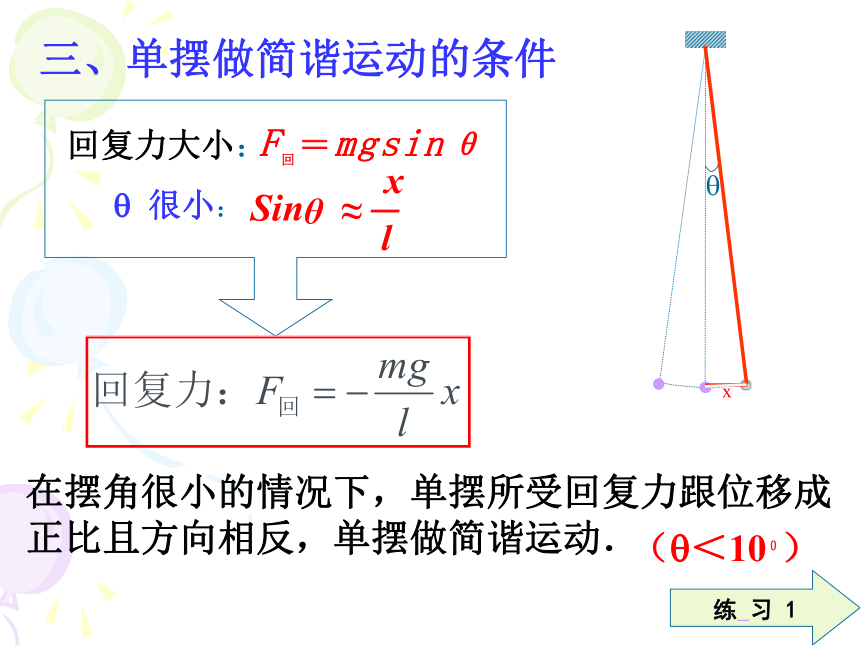
三、单摆做简谐运动的条件
回复力大小:
F回=mgsinθ
?
很小:
x
Sinθ
≈-
l
练
习
1
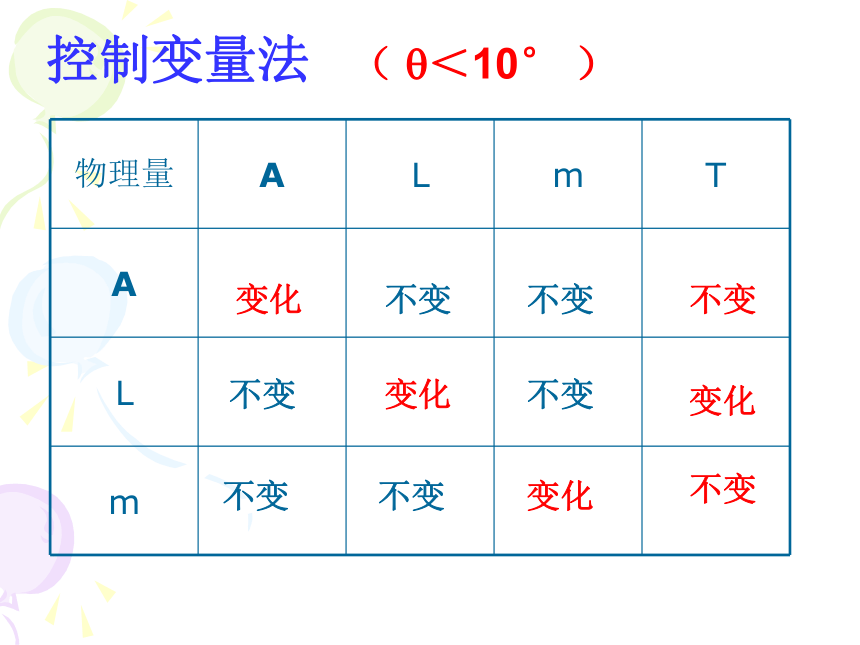
四.探究单摆做简谐运动振动的周期与哪些因素有关?
振幅A
摆长l
摆球质量m
控制变量法
物理量
A
L
m
T
A
L
m
(
?<10°
)
变化
不变
不变
不变
变化
不变
不变
变化
不变
不变
变化
不变
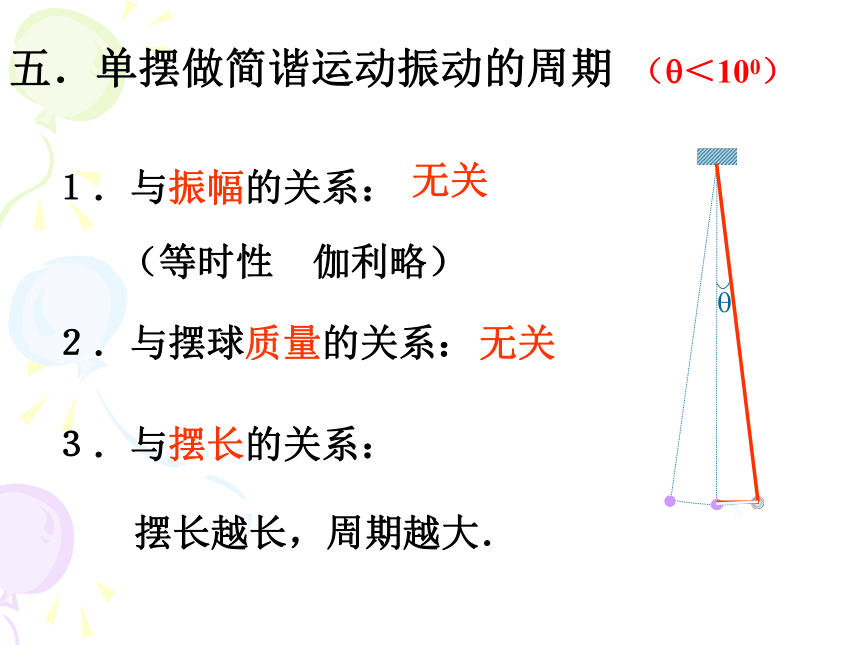
五.单摆做简谐运动振动的周期
1.与振幅的关系:
无关
2.与摆球质量的关系:
无关
3.与摆长的关系:
摆长越长,周期越大.
(等时性 伽利略)
?
x
(?<100)
荷兰物理学家惠更斯
单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关。
(1629---1695)
练
习
2
五.单摆做简谐运动振动的周期
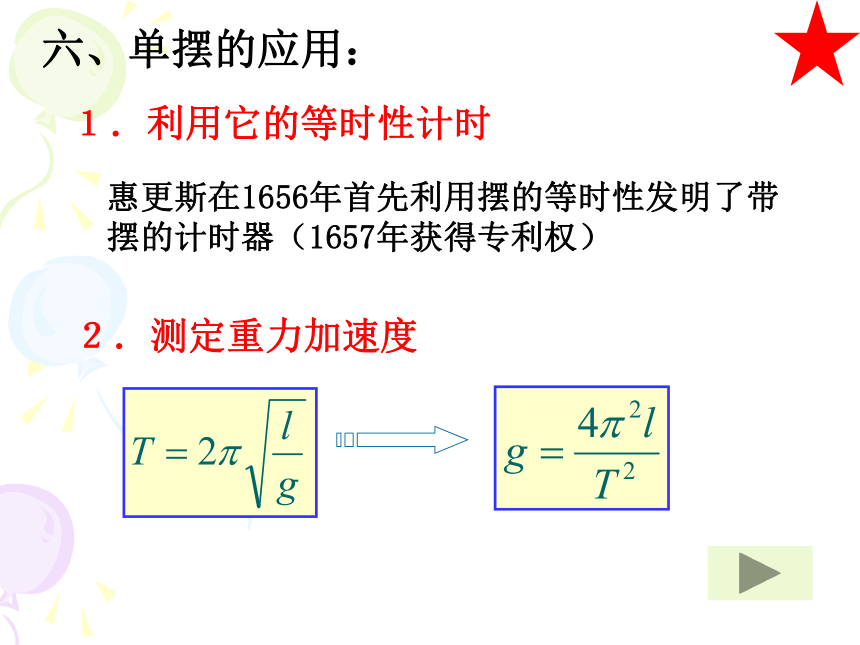
六、单摆的应用:
1.利用它的等时性计时
2.测定重力加速度
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)
小结:
1.在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多,这样的装置叫单摆.
2.在摆角很小的情况下,单摆所受回复力跟位移成正比且方向相反,单摆做简谐运动.
3.单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关.
1.在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多,这样的装置叫单摆。
2.在摆角很小的情况下,单摆所受回复力跟位移成正比且方向相反,单摆做简谐运动。
练习1:
2.单摆作简谐运动时的回复力是:
A.摆球的重力
B.摆球重力沿圆弧切线的分力
C.摆线的拉力
D.摆球重力与摆线拉力的合力
1.下列哪些材料能做成单摆:
A.长为1米的细线
B.
长为1米的橡皮条
C.直径为5厘米的泡沫塑料球
D.直径为1厘米的钢球
B
A
D
3.单摆的振动周期在发生下述哪些情况中增大:
A.摆球的质量增大
B.摆长增大
C.单摆由赤道移到北极
D.增大振幅
(?<100)
4.一个作简谐运动的单摆,周期是1秒:
A.摆长缩短为原来的1/4时,周期是0.5秒
B.摆球的质量减小为原来的1/4时,周期是4秒
C.振幅减为原来的1/4时周期是1秒
D.如果重力加速度减为原来的1/4时,周期是0.5秒.
练习2:
B
AC
5.由单摆作简谐运动的周期公式:
可知:
A.摆长无限减小,可以使振动周期接近于零
B.在月球表面的单摆周期一定比地球表面的单摆的周期长
C.单摆的振动周期与摆球的质量无关
D.单摆的振动周期与摆角无关,所以摆角可以是300
6.一摆长为L的单摆,在悬点正下方5L/9处有一钉子,则这个单摆的周期是
L
思考:
Bc
mg
T
mgCosθ
mgSinθ
返
回
回复力大小:
向心力大小:
单摆运动的受力分析
2.5实验:用单摆测定重力加速度
用单摆测定重力加速度
实验目的:用单摆测定当地重力加速度
学习使用秒表和游标卡尺
实验原理:
实验器材:带孔小钢球一个,约1m长的线绳一条,铁架台、米尺、游标卡尺、秒表
原理式
测量式
测量量
摆线长l0
摆球直径d
单摆摆动n个周期的时间t
秒表的读数
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
分两部分:
1、小圈内表示分,每小格表示
0.5分钟;
2、大圈内表示秒,最小刻度
为0.1秒。
3、当分针在前0.5分内时,秒针在0~30秒内读数;当分针在后0.5分内时,秒针在30~60秒内读数。
读数为4分48.7秒
注意秒表不估读
游标卡尺的构造
外测量爪
紧固螺钉
内测量爪
游标尺(副尺)
深度尺
主尺
0
5
10
0
1cm
10分度游标卡尺的刻度
1.主尺与刻度尺相同最小分度是1mm
2.游标尺上有10个小的等分刻度
总长等于9mm
3.游标尺的每一分度与主尺的最小分度相差
0.1mm
10分度游标卡尺的读数
游标的第一条刻度线与主尺的1mm刻度重合则左右测量爪相距多少?
0.1mm
0
5
10
0
1
0
5
10
0
1
游标的第二条刻度线与主尺的2mm刻度重合则左右测量爪相距多少?
0.2mm
游标的第几条刻度线与主尺的刻度线重合,副尺读数就是零点几毫米
10分度游标卡尺读数方法
如图游标的第一条刻度线与主尺的2mm刻度线重合,则左右测脚相距多少?
1.1mm
0
5
10
0
1
读数公式:
主尺上的副尺零刻线之前的整毫米数
+
n×0.1mm
副尺上与主尺上某刻线对齐的第n条刻线
0
5
10
0
1
0.3mm
0
5
10
0
1
1.4mm
10分度游标卡尺读数练习
0
5
10
0
1
4.1mm
0
5
10
0
1
10.5mm
10分度游标卡尺读数练习
1、将单摆一端固定在铁架台上
用米尺和卡尺测定单摆的摆长l
(摆线静挂时从悬点到球心的距离)
2、让单摆摆动(摆角小于5°),测定n(30—50)次全振动的时间t,求出单摆的平均周期
T=t/n
;
3、改变摆长3-4次重复步骤1、2
(摆长可选约1m、0.95m、0.90m、0.85m、0.80m)
用单摆测定重力加速度实验步骤
注意事项
用单摆测定重力加速度注意事项
1、悬点固定:摆线应夹紧在竹夹中,以免摆动时发生摆线下滑或悬点不固定,摆长改变的现象;
×
注意事项
用单摆测定重力加速度
2、摆球要在同一个竖直平面内摆动,不要形成圆锥摆;
3、注意摆动时摆角不易过大,不能超过10?,以保证单摆做简谐运动;
4、计算单摆的振动次数时,应以摆球通过最低点时开始计时,以后摆球从同一方向通过最低点时进行计数
5、为了减少偶然误差改变摆长,多次测量求平均值。
公式求解
描点作图:
改变摆长L,测出相应周期T,如图所示,
以L为横坐标
T2为纵坐标
用单摆测定重力加速度数据处理
9.86m/s2
1.0
4
3
2
0.8
0.5
0
L/m
T
2/s2
2.4
单
摆
复
习
提
问
1.机械振动
2.简谐运动
物体(或物体的一部分)在某一中心位置两侧所做的往复运动叫做机械振动。
物体在跟位移大小成正比、并且总是指向平衡位置的回复力作用下的振动,叫做简谐运动。
3.简谐运动的条件
F
=-
kX
一.单摆
在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多,这样的装置叫单摆。
悬点:
不可伸缩
固定
细线:
单摆是理想化的物理模型
L绳>>d小球
M绳
<<
M
小球
O’
二.单摆的运动
1.平衡位置
3.受力分析
重力
拉力
2.运动过程分析
以悬点O’为圆心的圆周运动
以点O为平衡位置的机械振动
4.力与运动的关系
回复力大小:
向心力大小:
点O
O’
O
回复力大小:
F回=mgsinθ
A
B
O
C
l
θ较大时:
Sinθ=
l
BC
?
很小时:
SIN
θ
=
x/
l
l
(
?
<5°)
在摆角很小的情况下,单摆所受回复力跟位移成正比且方向相反,单摆做简谐运动.
?
x
(?<100)
三、单摆做简谐运动的条件
回复力大小:
F回=mgsinθ
?
很小:
x
Sinθ
≈-
l
练
习
1
四.探究单摆做简谐运动振动的周期与哪些因素有关?
振幅A
摆长l
摆球质量m
控制变量法
物理量
A
L
m
T
A
L
m
(
?<10°
)
变化
不变
不变
不变
变化
不变
不变
变化
不变
不变
变化
不变
五.单摆做简谐运动振动的周期
1.与振幅的关系:
无关
2.与摆球质量的关系:
无关
3.与摆长的关系:
摆长越长,周期越大.
(等时性 伽利略)
?
x
(?<100)
荷兰物理学家惠更斯
单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关。
(1629---1695)
练
习
2
五.单摆做简谐运动振动的周期
六、单摆的应用:
1.利用它的等时性计时
2.测定重力加速度
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)
小结:
1.在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多,这样的装置叫单摆.
2.在摆角很小的情况下,单摆所受回复力跟位移成正比且方向相反,单摆做简谐运动.
3.单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关.
1.在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多,这样的装置叫单摆。
2.在摆角很小的情况下,单摆所受回复力跟位移成正比且方向相反,单摆做简谐运动。
练习1:
2.单摆作简谐运动时的回复力是:
A.摆球的重力
B.摆球重力沿圆弧切线的分力
C.摆线的拉力
D.摆球重力与摆线拉力的合力
1.下列哪些材料能做成单摆:
A.长为1米的细线
B.
长为1米的橡皮条
C.直径为5厘米的泡沫塑料球
D.直径为1厘米的钢球
B
A
D
3.单摆的振动周期在发生下述哪些情况中增大:
A.摆球的质量增大
B.摆长增大
C.单摆由赤道移到北极
D.增大振幅
(?<100)
4.一个作简谐运动的单摆,周期是1秒:
A.摆长缩短为原来的1/4时,周期是0.5秒
B.摆球的质量减小为原来的1/4时,周期是4秒
C.振幅减为原来的1/4时周期是1秒
D.如果重力加速度减为原来的1/4时,周期是0.5秒.
练习2:
B
AC
5.由单摆作简谐运动的周期公式:
可知:
A.摆长无限减小,可以使振动周期接近于零
B.在月球表面的单摆周期一定比地球表面的单摆的周期长
C.单摆的振动周期与摆球的质量无关
D.单摆的振动周期与摆角无关,所以摆角可以是300
6.一摆长为L的单摆,在悬点正下方5L/9处有一钉子,则这个单摆的周期是
L
思考:
Bc
mg
T
mgCosθ
mgSinθ
返
回
回复力大小:
向心力大小:
单摆运动的受力分析
2.5实验:用单摆测定重力加速度
用单摆测定重力加速度
实验目的:用单摆测定当地重力加速度
学习使用秒表和游标卡尺
实验原理:
实验器材:带孔小钢球一个,约1m长的线绳一条,铁架台、米尺、游标卡尺、秒表
原理式
测量式
测量量
摆线长l0
摆球直径d
单摆摆动n个周期的时间t
秒表的读数
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
分两部分:
1、小圈内表示分,每小格表示
0.5分钟;
2、大圈内表示秒,最小刻度
为0.1秒。
3、当分针在前0.5分内时,秒针在0~30秒内读数;当分针在后0.5分内时,秒针在30~60秒内读数。
读数为4分48.7秒
注意秒表不估读
游标卡尺的构造
外测量爪
紧固螺钉
内测量爪
游标尺(副尺)
深度尺
主尺
0
5
10
0
1cm
10分度游标卡尺的刻度
1.主尺与刻度尺相同最小分度是1mm
2.游标尺上有10个小的等分刻度
总长等于9mm
3.游标尺的每一分度与主尺的最小分度相差
0.1mm
10分度游标卡尺的读数
游标的第一条刻度线与主尺的1mm刻度重合则左右测量爪相距多少?
0.1mm
0
5
10
0
1
0
5
10
0
1
游标的第二条刻度线与主尺的2mm刻度重合则左右测量爪相距多少?
0.2mm
游标的第几条刻度线与主尺的刻度线重合,副尺读数就是零点几毫米
10分度游标卡尺读数方法
如图游标的第一条刻度线与主尺的2mm刻度线重合,则左右测脚相距多少?
1.1mm
0
5
10
0
1
读数公式:
主尺上的副尺零刻线之前的整毫米数
+
n×0.1mm
副尺上与主尺上某刻线对齐的第n条刻线
0
5
10
0
1
0.3mm
0
5
10
0
1
1.4mm
10分度游标卡尺读数练习
0
5
10
0
1
4.1mm
0
5
10
0
1
10.5mm
10分度游标卡尺读数练习
1、将单摆一端固定在铁架台上
用米尺和卡尺测定单摆的摆长l
(摆线静挂时从悬点到球心的距离)
2、让单摆摆动(摆角小于5°),测定n(30—50)次全振动的时间t,求出单摆的平均周期
T=t/n
;
3、改变摆长3-4次重复步骤1、2
(摆长可选约1m、0.95m、0.90m、0.85m、0.80m)
用单摆测定重力加速度实验步骤
注意事项
用单摆测定重力加速度注意事项
1、悬点固定:摆线应夹紧在竹夹中,以免摆动时发生摆线下滑或悬点不固定,摆长改变的现象;
×
注意事项
用单摆测定重力加速度
2、摆球要在同一个竖直平面内摆动,不要形成圆锥摆;
3、注意摆动时摆角不易过大,不能超过10?,以保证单摆做简谐运动;
4、计算单摆的振动次数时,应以摆球通过最低点时开始计时,以后摆球从同一方向通过最低点时进行计数
5、为了减少偶然误差改变摆长,多次测量求平均值。
公式求解
描点作图:
改变摆长L,测出相应周期T,如图所示,
以L为横坐标
T2为纵坐标
用单摆测定重力加速度数据处理
9.86m/s2
1.0
4
3
2
0.8
0.5
0
L/m
T
2/s2
