2020-2021学年北师大版七年级数学下册5.2探索轴对称的性质-同步提升训练(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册5.2探索轴对称的性质-同步提升训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 330.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 21:27:44 | ||
图片预览



文档简介
2021年度北师大版七年级数学下册《5.2探索轴对称的性质》同步提升训练(附答案)
1.“折叠”是数学上常见构造新图形的重要方法如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿图中标示的DE折叠,点A恰好落在边BC的点G处,若∠CDG=52°,则∠DEG的度数为( )
A.73° B.71° C.68° D.52°
2.如图,在△ABC中,点D在AC上,沿AC将△ABC对折,点B与点E重合,则图中全等的三角形有( )
A.3对 B.2对 C.4对 D.1对
3.如图,在△ABC中,点D是BC上的点,AD=BD,将△ABD沿AD翻折得到△AED,若∠B=40°,则∠CDE等于( )
A.20° B.30° C.35° D.40°
4.如图,在△ABC中,点D,E分别在边AB,BC上,点A与点E关于直线CD对称.若AB=7,AC=9,BC=12,则△DBE的周长为( )
A.9 B.10 C.11 D.12
5.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形可以画出( )
A.6个 B.5个 C.4个 D.3个
6.如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
A.80° B.60° C.40° D.30°
7.如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为18,△ECF的周长为6,四边形纸片ABCD的周长为( )
A.20 B.24 C.32 D.48
8.如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折形成的,若∠1:∠2:∠3=13:3:2,CD与BE交于O点,则∠EOC的度数为( )
A.80° B.85° C.90° D.100°
9.如图,在△ABC中,∠BAC=68°,∠C=36°,AD平分∠BAC,M、N分别是AD、AB上的动点,当BM+MN最小时,∠BMN的度数为( )
A.34° B.68° C.76° D.90°
10.如图,四边形ABCD中,∠A=∠C=90°,点M、N分别是BC、AB边上的动点,∠B=56°,当△DMN的周长最小值时,则∠MDN的度数是( )
A.124° B.68° C.60° D.56°
11.如图,△ABD和△ABC关于直线AD对称,若S△ABC=12,则图中阴影部分面积为 .
12.如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=35°,将△ABD沿着AD翻折得到△AED,则∠CDE= °.
13.如图,在△ABC中,CD平分∠ACB,点E,F分别是CD,AC上的动点.若BC=6,S△ABC=12,则AE+EF的最小值是 .
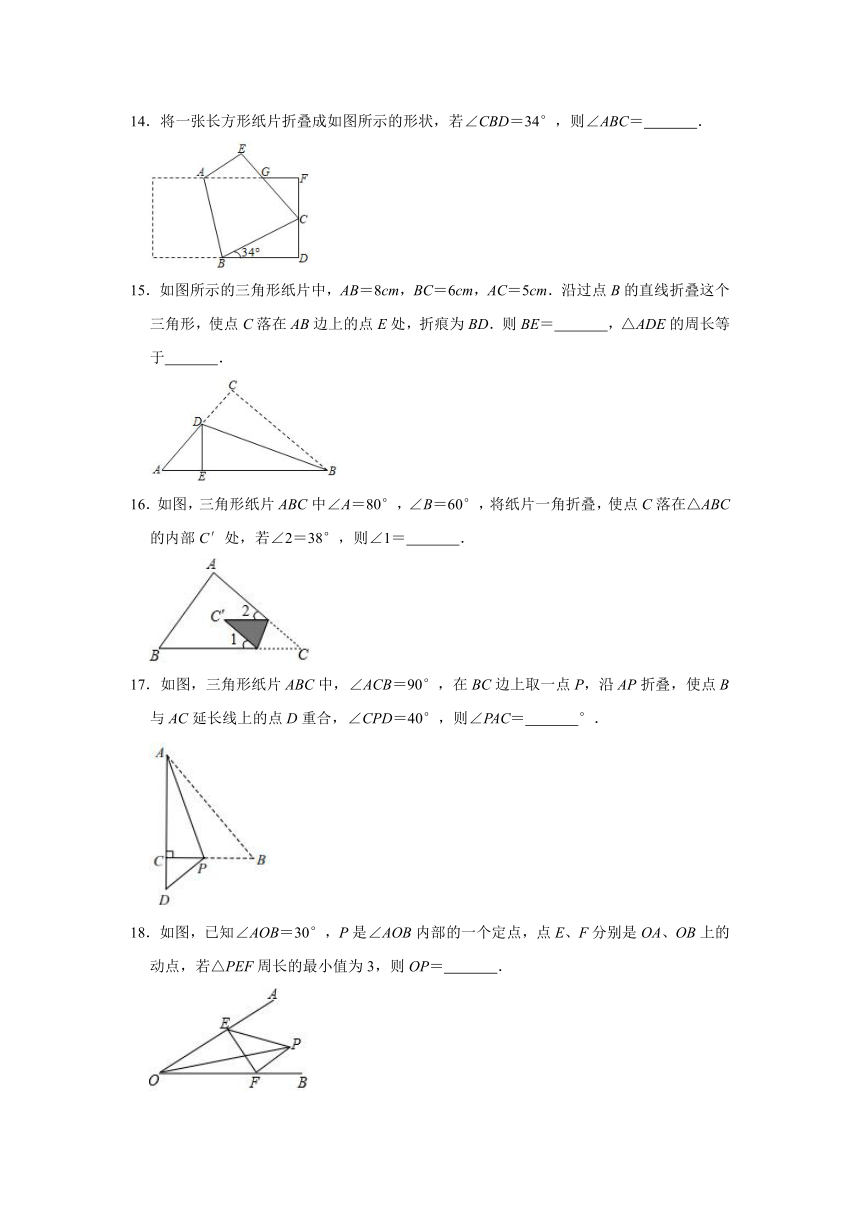
14.将一张长方形纸片折叠成如图所示的形状,若∠CBD=34°,则∠ABC= .
15.如图所示的三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD.则BE= ,△ADE的周长等于 .
16.如图,三角形纸片ABC中∠A=80°,∠B=60°,将纸片一角折叠,使点C落在△ABC的内部C′处,若∠2=38°,则∠1= .
17.如图,三角形纸片ABC中,∠ACB=90°,在BC边上取一点P,沿AP折叠,使点B与AC延长线上的点D重合,∠CPD=40°,则∠PAC= °.
18.如图,已知∠AOB=30°,P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点,若△PEF周长的最小值为3,则OP= .
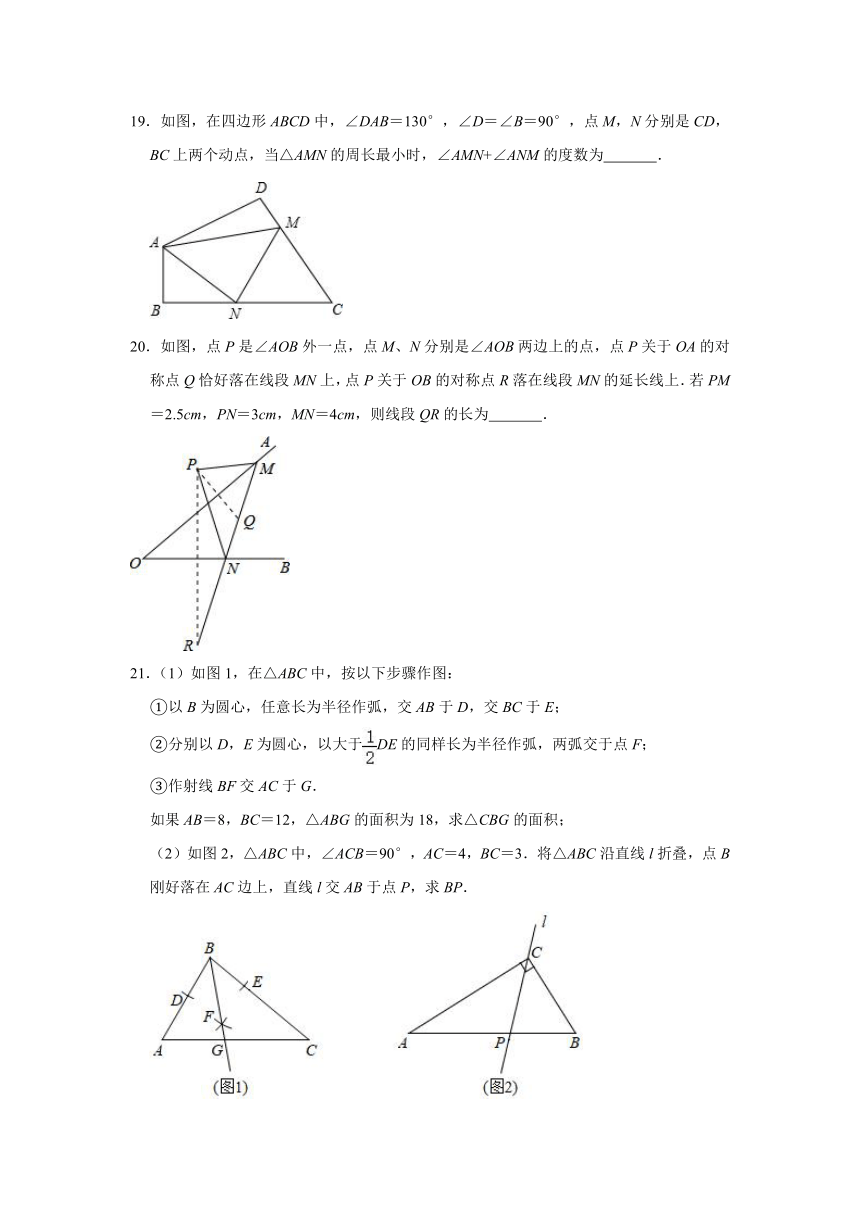
19.如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为 .
20.如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为 .
21.(1)如图1,在△ABC中,按以下步骤作图:
①以B为圆心,任意长为半径作弧,交AB于D,交BC于E;
②分别以D,E为圆心,以大于DE的同样长为半径作弧,两弧交于点F;
③作射线BF交AC于G.
如果AB=8,BC=12,△ABG的面积为18,求△CBG的面积;
(2)如图2,△ABC中,∠ACB=90°,AC=4,BC=3.将△ABC沿直线l折叠,点B刚好落在AC边上,直线l交AB于点P,求BP.
22.如图,点P关于OA、OB轴对称的对称点分别为C、D,连接CD,交OA于M,交OB于N.
(1)若CD的长为18厘米,求△PMN的周长;
(2)若∠C=21°,∠D=28°,求∠MPN的度数.
23.如图,P、Q为△ABC的边AB、AC上的两定点,在BC上求作一点M,使△PQM的周长最短(不写作法).
24.在△ABC中,∠ABC=45°,∠BAC=15°,将△ACB沿直线AC翻折至△ABC所在的平面内,得△ACD.过点A作AE,使∠DAE=∠DAC,与CD的延长线交于点E.
(1)如图①,求∠ACD,∠E的大小;
(2)如图②,连接BE,求证AB⊥BE.
25.折纸,是生活中一种常见的操作.通过折纸,可以直观的发现一些线段之间的数量关系.小明现有两张△ABC纸片,∠C=2∠B,进行了如下的操作:
(1)操作一:如图1,小明拿出第一张△ABC纸片,将边AC沿直线AD折叠,使点C落在边BC上,求证:AC+CD=BD;
(2)操作二:如图2,小明拿出第二张△ABC纸片,将边AC沿直线AD折叠,使点C落在边AB上,判断AC、CD和AB的数量关系并证明.
26.已知△ABC,∠ABC=80°,点E在BC边上,点D是射线AB上的一个动点,将△BDE沿DE折叠,使点B落在点B'处.
(1)如图1,若∠ADB'=125°,求∠CEB'的度数;
(2)如图2.试探究∠ADB'与∠CEB'的数量关系,并说明理由;
(3)连接CB',当CB'∥AB时,直接写出∠CB'E与∠ADB'的数量关系为 .
参考答案
1.解:∵∠CDG=52°,
∴∠ADG=90°﹣∠CDG=90°﹣52°=38°,
又∵∠ADE=∠GDE===19°,∠DAE=∠DGE=90°,
∴∠DEG=90°﹣∠GDE=90°﹣19°=71°.
故选:B.
2.解:∵沿AC将△ABC对折,点B与点E重合,
∴△ABC≌△AEC,
∴AB=AE,BC=CE,∠BAC=∠CAE,∠ACB=∠ACE,
在△ABD和△AED中,
,
∴△ABD≌△AED(SAS),
同理可得△BCD≌△ECD,
∴全等的三角形有3对,
故选:A.
3.解:∵AD=BD,
∴∠BAD=∠ABC=40°,
∵将△ABD沿着AD翻折得到△AED,
∴∠ADC=∠ABC+∠BAD=40°+40°=80°,∠ADE=∠ADB=180°﹣∠ABC﹣∠BAD=180°﹣40°﹣40°=100°,
∴∠CDE=100°﹣80°=20°,
故选:A.
4.解:∵点A与点E关于直线CD对称,
∴AD=DE,AC=CE=9,
∵AB=7,AC=9,BC=12,
∴△DBE的周长=BD+DE+BE=BD+AD+BC﹣AC=AB+BC﹣AC=7+12﹣9=10.
故选:B.
5.解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故选:A.
6.解:根据折叠的性质可得BD=DE,AB=AE.
∵AC=AE+EC,AB+BD=AC,
∴DE=EC.
∴∠EDC=∠C=20°,
∴∠AED=∠EDC+∠C=40°.
故选:C.
7.解:由折叠的性质知,AF=AB,EF=BE.
所以矩形的周长等于△AFD和△CFE的周长的和为18+6=24.
故矩形ABCD的周长为24.
故选:B.
8.解:如图,AE与DC交于点P,
∵∠1:∠2:∠3=13:3:2,
∴∠1=130°,∠3=20°,
∴∠DCA=20°,∠EAB=130°,
∵∠PAC=360°﹣2∠1=100°,
∴∠EPD=∠APC=180°﹣∠PAC﹣∠DCA=60°.
由翻折的性质可知∠E=∠3=20°.
∴∠EOC=180°﹣∠EPD﹣∠E=180°﹣60°﹣20°=100°.
故选:D.
9.解:∵∠BAC=68°,∠C=36°,
∴∠ABC=180°﹣68°﹣36°=76°,
如图,过B作BE⊥AC于E,交AD于M,
在AB上截取AN=AE,连接MN,
∵∠BAC的平分线交BC于点D,
∴∠EAM=∠NAM,
在△AME与△AMN中,
,
∴△AME≌△AMN(SAS),
∴ME=MN.∠ANM=∠AEM,
∴BM+MN=BM+ME=BE,
BM+MN最小值,只要求BM+EM的最小值,
当BE⊥AC时,BM+ME最小,
此时∠ABE=90°﹣68°=22°,
∴∠ANM=90°,
∴∠BMN=90°﹣22°=68°
故选:B.
10.解:延长DA到E使DA=AE,延长DC到F,使CF=DC,连接EF交AB于N,交BC于M,
此时,△DMN的周长最小,
∵AB⊥AD,BC⊥DC,
∴∠DAB=∠DCB=90°,
DM=FM,DN=EN,
∴∠E=∠ADN,∠F=∠CDM,
∵∠B=56°,
∴∠ADC=124°,
设∠MDN=α,
∴∠ADN+∠CDM=124°﹣α
∴∠DNM+∠DMN=2(124°﹣α),
∴α+2(124°﹣α)=180°,
解得:α=68°,
故选:B.
11.解:∵△ABD和△ABC关于直线AD对称,
∴S△BEF=S△CEF,
∴S阴=S△ADC=S△ABC=6.
故答案为:6.
12.解:∵∠BAD=∠ABC=35°,
∴∠ADC=∠BAD+∠ABC=35°+35°=70°,∠ADB=180°﹣35°﹣35°=110°,
∵将△ABD沿着AD翻折得到△AED,
∴∠ADE=∠ADB=110°,
∴∠CDE=∠ADE﹣∠ADC=110°﹣70°=40°,
故答案为:40.
13.解:作A关于CD的对称点H,
∵CD是△ABC的角平分线,
∴点H一定在BC上,
过H作HF⊥AC于F,交CD于E,
则此时,AE+EF的值最小,AE+EF的最小值=HF,
过A作AG⊥BC于G,
∵△ABC的面积为12,BC长为6,
∴AG=4,
∵CD垂直平分AH,
∴AC=CH,
∴S△ACH=AC?HF=CH?AG,
∴HF=AG=4,
∴AE+EF的最小值是4,
故答案为:4.
14.解:如图,由折叠的性质可得:∠ABC'=∠ABC,
∵∠ABC'+∠ABC+∠CBD=180°,
∴∠ABC=73°,
故答案为:73°.
15.解:∵折叠这个三角形点C落在AB边上的点E处,折痕为BD,
∴BE=BC=6cm,DE=CD,
∴AE=AB﹣BE=AB﹣BC=8﹣6=2(cm),
∴△ADE的周长=AD+DE+AE=AD+CD+AE=AC+AE,=5+2,=7(cm).
故答案为:6cm;7cm.
16.解:设折痕为EF,连接CC′.
∵∠2=∠ECC′+∠EC′C,∠1=∠FCC′+∠FC′C,∠ECF=∠EC′F,
∴∠1+∠2=2∠ECF,
∵∠C=180°﹣∠A﹣∠B=180°﹣80°﹣60°=40°,
∴∠1=80°﹣38°=42°,
故答案为:42°.
17.解:∵△APB沿AP折叠,
∴∠DAP=∠BAP,∠D=∠B,
∵∠CPD=40°,∠ACB=90°,
∴∠D=∠ACB﹣∠CPD=90°﹣40°=50°,
∴∠B=50°,
∴∠DAB=90°﹣∠B=90°﹣50°=40°,
∴∠PAC=∠DAB=×40°=20°.
故答案为:20.
18.解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点E、F,连接OP、OC、OD、PE、PF.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PE=CE,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PF=DF,OP=OD,∠DOB=∠POB,
∴OC=OD=OP,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD.
∴△PEF的周长的最小值=PE+EF+PF=CE+EF+DF≥CD=3.
∴OP=3,
故答案为3.
19.解:如图,
作点A关于BC的对称点A′,关于CD的对称点A″,
连接A′A″与BC、CD的交点即为所求的点N、M,
∵∠BAD=130°,∠B=∠D=90°,
∴∠A′+∠A″=180°﹣∠130°=50°,
由轴对称的性质得:∠A′=∠A′AN,∠A″=∠A″AM,
∴∠AMN+∠ANM=2(∠A′+∠A″)=2×50°=100°.
故答案为:100°
20.解:由轴对称的性质可知:PM=MQ=2.5cm,PN=RN=3cm,
QN=MN﹣QM=4﹣2.5=1.5cm,QR=QN+NR=1.5+3=4.5cm.
故答案为:4.5cm.
21.解:(1)如图,过点G作GM⊥AB于M,GN⊥BC于N.
∵BG平分∠ABC,
∴GM=GN,
∵S△ABG=?AB?GM=18,
∴GM=,
∴GN=GM=,
∴S△BCG=?BC?GN=×12×=27.
(2)如图,过点P作PG⊥AC于G,PH⊥BC于H.
由翻折的性质可知,PC平分∠ACB,
∴PG=PH,
∵∠ACB=90°,AC=4,BC=3,
∴AB===5,
∵====,
∴PB=AB=.
22.解:(1)∵点P关于OA,OB的轴对称点分别为C、D,连接CD,交OA于M,交OB于N,
∴PM=CM,ND=NP,
∵△PMN的周长=PN+PM+MN,PN+PM+MN=CD=18cm,
∴△PMN的周长为:18cm;
(2))∵P关于OA、OB的对称,
∴OA垂直平分PC,OB垂直平分PD,
∴CM=PM,PN=DN,
∴∠C=∠MPC,∠D=∠NPD,
∵∠PRM=∠PTN=90°,
∴在四边形OTPR中,∠CPD+∠O=180°,
∵∠D+∠C+∠CPD=180°,
∴∠C+∠D=∠O=49°,
∴∠MPN=180°﹣49°×2=82°.
23.解:如图,作点P关于BC的对称点P′,连接P′Q,交BC于点M,点M是所求的点.
24.解:(1)∵∠ABC=45°,∠BAC=15°,
∴∠ACB=120°,
∵将△ACB沿直线AC翻折,
∴∠B=∠ADC=45°,∠CAD=∠BAC=15°,∠ACB=∠ACD=120°,
∵∠DAE=∠DAC=15°,
∴∠E=∠ADC﹣∠DAE=30°;
(2)∵∠CAE=∠CAD+∠DAE=30°,
∴∠E=∠CAE=30°,
∴AC=CE,
∵∠ACB=∠ACD=120°,
∴∠BCE=120°=∠ACB,
在△ABC和△EBC中,
,
∴△ABC≌△EBC(SAS),
∴∠ABC=∠EBC=45°,
∴∠ABE=90°,
∴AB⊥BE.
25.(1)证明:如图1中,在DB上取一点T,使得DT=DC,连接AT.
∵AD⊥CT,DT=DC,
∴AT=AC,
∴∠ATC=∠C,
∵∠C=2∠B,
∴∠ATC=∠B+∠TAB=2∠B,
∴∠B=∠TAB,
∴TA=TB,
∴AC+CD=DT+BT=BD.
(2)解:结论:AC+CD=AB.
理由:如图2中,在线段AB上取一点H,使得AH=AC,连接DH.
由折叠可知,∠DAH=∠DAC,
在△ADH和△ADC中,
,
∴△ADH≌△ADC(SAS),
∴DH=DC,∠AHD=∠C,
∵∠C=2∠B,
∴∠AHD=∠B+∠HDB=2∠B,
∴∠B=∠HDB,
∴HB=HD=DC,
∴AC+CD=AH+BH=AB.
26.解:(1)如图1中,连接BB′.
由翻折的性质可知,∠DBE=∠DB′E=80°,
∵∠ADB′=∠DBB′+∠DB′B=125°,
∴∠EBB′+∠EB′B=160°﹣125°=35°,
∴∠CEB′=∠EBB′+∠EB′B=35°.
(2)结论:∠CEB′=∠ADB′+20°.
理由:如图2中,
∵∠ADB′+∠BEB′=360°﹣2×(180°﹣80°),
∴∠ADB′+180°﹣∠CEB′=160°,
∴∠CEB′=∠ADB′+20°.
(3)如图1﹣1中,当点D在线段AB上时,结论:∠CB′E+80°=∠ADB′
理由:连接CB′.
∵CB′∥AB,
∴∠ADB′=∠CB′D,
由翻折可知,∠B=∠DB′E=80°,
∴∠CB′E+80°=∠CB′D=∠ADB′.
如图2中,当点D在AB的延长线上时,结论:∠CB′E+∠ADB′=80°.
理由:连接CB′.
∵CB′∥AD,
∴∠ADB′+∠DB′C=180°,
∵∠ABC=80°,
∴∠DBE=∠DB′E=100°,
∴∠CB′E+100°+∠ADB′=180°,
∴∠CB′E+∠ADB′=80°.
综上所述,∠CB'E与∠ADB'的数量关系为∠CB′E+80°=∠ADB′或∠CB′E+∠ADB′=80°.
故答案为:∠CB′E+80°=∠ADB′或∠CB′E+∠ADB′=80°
1.“折叠”是数学上常见构造新图形的重要方法如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿图中标示的DE折叠,点A恰好落在边BC的点G处,若∠CDG=52°,则∠DEG的度数为( )
A.73° B.71° C.68° D.52°
2.如图,在△ABC中,点D在AC上,沿AC将△ABC对折,点B与点E重合,则图中全等的三角形有( )
A.3对 B.2对 C.4对 D.1对
3.如图,在△ABC中,点D是BC上的点,AD=BD,将△ABD沿AD翻折得到△AED,若∠B=40°,则∠CDE等于( )
A.20° B.30° C.35° D.40°
4.如图,在△ABC中,点D,E分别在边AB,BC上,点A与点E关于直线CD对称.若AB=7,AC=9,BC=12,则△DBE的周长为( )
A.9 B.10 C.11 D.12
5.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形可以画出( )
A.6个 B.5个 C.4个 D.3个
6.如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
A.80° B.60° C.40° D.30°
7.如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为18,△ECF的周长为6,四边形纸片ABCD的周长为( )
A.20 B.24 C.32 D.48
8.如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折形成的,若∠1:∠2:∠3=13:3:2,CD与BE交于O点,则∠EOC的度数为( )
A.80° B.85° C.90° D.100°
9.如图,在△ABC中,∠BAC=68°,∠C=36°,AD平分∠BAC,M、N分别是AD、AB上的动点,当BM+MN最小时,∠BMN的度数为( )
A.34° B.68° C.76° D.90°
10.如图,四边形ABCD中,∠A=∠C=90°,点M、N分别是BC、AB边上的动点,∠B=56°,当△DMN的周长最小值时,则∠MDN的度数是( )
A.124° B.68° C.60° D.56°
11.如图,△ABD和△ABC关于直线AD对称,若S△ABC=12,则图中阴影部分面积为 .
12.如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=35°,将△ABD沿着AD翻折得到△AED,则∠CDE= °.
13.如图,在△ABC中,CD平分∠ACB,点E,F分别是CD,AC上的动点.若BC=6,S△ABC=12,则AE+EF的最小值是 .
14.将一张长方形纸片折叠成如图所示的形状,若∠CBD=34°,则∠ABC= .
15.如图所示的三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD.则BE= ,△ADE的周长等于 .
16.如图,三角形纸片ABC中∠A=80°,∠B=60°,将纸片一角折叠,使点C落在△ABC的内部C′处,若∠2=38°,则∠1= .
17.如图,三角形纸片ABC中,∠ACB=90°,在BC边上取一点P,沿AP折叠,使点B与AC延长线上的点D重合,∠CPD=40°,则∠PAC= °.
18.如图,已知∠AOB=30°,P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点,若△PEF周长的最小值为3,则OP= .
19.如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为 .
20.如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为 .
21.(1)如图1,在△ABC中,按以下步骤作图:
①以B为圆心,任意长为半径作弧,交AB于D,交BC于E;
②分别以D,E为圆心,以大于DE的同样长为半径作弧,两弧交于点F;
③作射线BF交AC于G.
如果AB=8,BC=12,△ABG的面积为18,求△CBG的面积;
(2)如图2,△ABC中,∠ACB=90°,AC=4,BC=3.将△ABC沿直线l折叠,点B刚好落在AC边上,直线l交AB于点P,求BP.
22.如图,点P关于OA、OB轴对称的对称点分别为C、D,连接CD,交OA于M,交OB于N.
(1)若CD的长为18厘米,求△PMN的周长;
(2)若∠C=21°,∠D=28°,求∠MPN的度数.
23.如图,P、Q为△ABC的边AB、AC上的两定点,在BC上求作一点M,使△PQM的周长最短(不写作法).
24.在△ABC中,∠ABC=45°,∠BAC=15°,将△ACB沿直线AC翻折至△ABC所在的平面内,得△ACD.过点A作AE,使∠DAE=∠DAC,与CD的延长线交于点E.
(1)如图①,求∠ACD,∠E的大小;
(2)如图②,连接BE,求证AB⊥BE.
25.折纸,是生活中一种常见的操作.通过折纸,可以直观的发现一些线段之间的数量关系.小明现有两张△ABC纸片,∠C=2∠B,进行了如下的操作:
(1)操作一:如图1,小明拿出第一张△ABC纸片,将边AC沿直线AD折叠,使点C落在边BC上,求证:AC+CD=BD;
(2)操作二:如图2,小明拿出第二张△ABC纸片,将边AC沿直线AD折叠,使点C落在边AB上,判断AC、CD和AB的数量关系并证明.
26.已知△ABC,∠ABC=80°,点E在BC边上,点D是射线AB上的一个动点,将△BDE沿DE折叠,使点B落在点B'处.
(1)如图1,若∠ADB'=125°,求∠CEB'的度数;
(2)如图2.试探究∠ADB'与∠CEB'的数量关系,并说明理由;
(3)连接CB',当CB'∥AB时,直接写出∠CB'E与∠ADB'的数量关系为 .
参考答案
1.解:∵∠CDG=52°,
∴∠ADG=90°﹣∠CDG=90°﹣52°=38°,
又∵∠ADE=∠GDE===19°,∠DAE=∠DGE=90°,
∴∠DEG=90°﹣∠GDE=90°﹣19°=71°.
故选:B.
2.解:∵沿AC将△ABC对折,点B与点E重合,
∴△ABC≌△AEC,
∴AB=AE,BC=CE,∠BAC=∠CAE,∠ACB=∠ACE,
在△ABD和△AED中,
,
∴△ABD≌△AED(SAS),
同理可得△BCD≌△ECD,
∴全等的三角形有3对,
故选:A.
3.解:∵AD=BD,
∴∠BAD=∠ABC=40°,
∵将△ABD沿着AD翻折得到△AED,
∴∠ADC=∠ABC+∠BAD=40°+40°=80°,∠ADE=∠ADB=180°﹣∠ABC﹣∠BAD=180°﹣40°﹣40°=100°,
∴∠CDE=100°﹣80°=20°,
故选:A.
4.解:∵点A与点E关于直线CD对称,
∴AD=DE,AC=CE=9,
∵AB=7,AC=9,BC=12,
∴△DBE的周长=BD+DE+BE=BD+AD+BC﹣AC=AB+BC﹣AC=7+12﹣9=10.
故选:B.
5.解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故选:A.
6.解:根据折叠的性质可得BD=DE,AB=AE.
∵AC=AE+EC,AB+BD=AC,
∴DE=EC.
∴∠EDC=∠C=20°,
∴∠AED=∠EDC+∠C=40°.
故选:C.
7.解:由折叠的性质知,AF=AB,EF=BE.
所以矩形的周长等于△AFD和△CFE的周长的和为18+6=24.
故矩形ABCD的周长为24.
故选:B.
8.解:如图,AE与DC交于点P,
∵∠1:∠2:∠3=13:3:2,
∴∠1=130°,∠3=20°,
∴∠DCA=20°,∠EAB=130°,
∵∠PAC=360°﹣2∠1=100°,
∴∠EPD=∠APC=180°﹣∠PAC﹣∠DCA=60°.
由翻折的性质可知∠E=∠3=20°.
∴∠EOC=180°﹣∠EPD﹣∠E=180°﹣60°﹣20°=100°.
故选:D.
9.解:∵∠BAC=68°,∠C=36°,
∴∠ABC=180°﹣68°﹣36°=76°,
如图,过B作BE⊥AC于E,交AD于M,
在AB上截取AN=AE,连接MN,
∵∠BAC的平分线交BC于点D,
∴∠EAM=∠NAM,
在△AME与△AMN中,
,
∴△AME≌△AMN(SAS),
∴ME=MN.∠ANM=∠AEM,
∴BM+MN=BM+ME=BE,
BM+MN最小值,只要求BM+EM的最小值,
当BE⊥AC时,BM+ME最小,
此时∠ABE=90°﹣68°=22°,
∴∠ANM=90°,
∴∠BMN=90°﹣22°=68°
故选:B.
10.解:延长DA到E使DA=AE,延长DC到F,使CF=DC,连接EF交AB于N,交BC于M,
此时,△DMN的周长最小,
∵AB⊥AD,BC⊥DC,
∴∠DAB=∠DCB=90°,
DM=FM,DN=EN,
∴∠E=∠ADN,∠F=∠CDM,
∵∠B=56°,
∴∠ADC=124°,
设∠MDN=α,
∴∠ADN+∠CDM=124°﹣α
∴∠DNM+∠DMN=2(124°﹣α),
∴α+2(124°﹣α)=180°,
解得:α=68°,
故选:B.
11.解:∵△ABD和△ABC关于直线AD对称,
∴S△BEF=S△CEF,
∴S阴=S△ADC=S△ABC=6.
故答案为:6.
12.解:∵∠BAD=∠ABC=35°,
∴∠ADC=∠BAD+∠ABC=35°+35°=70°,∠ADB=180°﹣35°﹣35°=110°,
∵将△ABD沿着AD翻折得到△AED,
∴∠ADE=∠ADB=110°,
∴∠CDE=∠ADE﹣∠ADC=110°﹣70°=40°,
故答案为:40.
13.解:作A关于CD的对称点H,
∵CD是△ABC的角平分线,
∴点H一定在BC上,
过H作HF⊥AC于F,交CD于E,
则此时,AE+EF的值最小,AE+EF的最小值=HF,
过A作AG⊥BC于G,
∵△ABC的面积为12,BC长为6,
∴AG=4,
∵CD垂直平分AH,
∴AC=CH,
∴S△ACH=AC?HF=CH?AG,
∴HF=AG=4,
∴AE+EF的最小值是4,
故答案为:4.
14.解:如图,由折叠的性质可得:∠ABC'=∠ABC,
∵∠ABC'+∠ABC+∠CBD=180°,
∴∠ABC=73°,
故答案为:73°.
15.解:∵折叠这个三角形点C落在AB边上的点E处,折痕为BD,
∴BE=BC=6cm,DE=CD,
∴AE=AB﹣BE=AB﹣BC=8﹣6=2(cm),
∴△ADE的周长=AD+DE+AE=AD+CD+AE=AC+AE,=5+2,=7(cm).
故答案为:6cm;7cm.
16.解:设折痕为EF,连接CC′.
∵∠2=∠ECC′+∠EC′C,∠1=∠FCC′+∠FC′C,∠ECF=∠EC′F,
∴∠1+∠2=2∠ECF,
∵∠C=180°﹣∠A﹣∠B=180°﹣80°﹣60°=40°,
∴∠1=80°﹣38°=42°,
故答案为:42°.
17.解:∵△APB沿AP折叠,
∴∠DAP=∠BAP,∠D=∠B,
∵∠CPD=40°,∠ACB=90°,
∴∠D=∠ACB﹣∠CPD=90°﹣40°=50°,
∴∠B=50°,
∴∠DAB=90°﹣∠B=90°﹣50°=40°,
∴∠PAC=∠DAB=×40°=20°.
故答案为:20.
18.解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点E、F,连接OP、OC、OD、PE、PF.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PE=CE,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PF=DF,OP=OD,∠DOB=∠POB,
∴OC=OD=OP,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD.
∴△PEF的周长的最小值=PE+EF+PF=CE+EF+DF≥CD=3.
∴OP=3,
故答案为3.
19.解:如图,
作点A关于BC的对称点A′,关于CD的对称点A″,
连接A′A″与BC、CD的交点即为所求的点N、M,
∵∠BAD=130°,∠B=∠D=90°,
∴∠A′+∠A″=180°﹣∠130°=50°,
由轴对称的性质得:∠A′=∠A′AN,∠A″=∠A″AM,
∴∠AMN+∠ANM=2(∠A′+∠A″)=2×50°=100°.
故答案为:100°
20.解:由轴对称的性质可知:PM=MQ=2.5cm,PN=RN=3cm,
QN=MN﹣QM=4﹣2.5=1.5cm,QR=QN+NR=1.5+3=4.5cm.
故答案为:4.5cm.
21.解:(1)如图,过点G作GM⊥AB于M,GN⊥BC于N.
∵BG平分∠ABC,
∴GM=GN,
∵S△ABG=?AB?GM=18,
∴GM=,
∴GN=GM=,
∴S△BCG=?BC?GN=×12×=27.
(2)如图,过点P作PG⊥AC于G,PH⊥BC于H.
由翻折的性质可知,PC平分∠ACB,
∴PG=PH,
∵∠ACB=90°,AC=4,BC=3,
∴AB===5,
∵====,
∴PB=AB=.
22.解:(1)∵点P关于OA,OB的轴对称点分别为C、D,连接CD,交OA于M,交OB于N,
∴PM=CM,ND=NP,
∵△PMN的周长=PN+PM+MN,PN+PM+MN=CD=18cm,
∴△PMN的周长为:18cm;
(2))∵P关于OA、OB的对称,
∴OA垂直平分PC,OB垂直平分PD,
∴CM=PM,PN=DN,
∴∠C=∠MPC,∠D=∠NPD,
∵∠PRM=∠PTN=90°,
∴在四边形OTPR中,∠CPD+∠O=180°,
∵∠D+∠C+∠CPD=180°,
∴∠C+∠D=∠O=49°,
∴∠MPN=180°﹣49°×2=82°.
23.解:如图,作点P关于BC的对称点P′,连接P′Q,交BC于点M,点M是所求的点.
24.解:(1)∵∠ABC=45°,∠BAC=15°,
∴∠ACB=120°,
∵将△ACB沿直线AC翻折,
∴∠B=∠ADC=45°,∠CAD=∠BAC=15°,∠ACB=∠ACD=120°,
∵∠DAE=∠DAC=15°,
∴∠E=∠ADC﹣∠DAE=30°;
(2)∵∠CAE=∠CAD+∠DAE=30°,
∴∠E=∠CAE=30°,
∴AC=CE,
∵∠ACB=∠ACD=120°,
∴∠BCE=120°=∠ACB,
在△ABC和△EBC中,
,
∴△ABC≌△EBC(SAS),
∴∠ABC=∠EBC=45°,
∴∠ABE=90°,
∴AB⊥BE.
25.(1)证明:如图1中,在DB上取一点T,使得DT=DC,连接AT.
∵AD⊥CT,DT=DC,
∴AT=AC,
∴∠ATC=∠C,
∵∠C=2∠B,
∴∠ATC=∠B+∠TAB=2∠B,
∴∠B=∠TAB,
∴TA=TB,
∴AC+CD=DT+BT=BD.
(2)解:结论:AC+CD=AB.
理由:如图2中,在线段AB上取一点H,使得AH=AC,连接DH.
由折叠可知,∠DAH=∠DAC,
在△ADH和△ADC中,
,
∴△ADH≌△ADC(SAS),
∴DH=DC,∠AHD=∠C,
∵∠C=2∠B,
∴∠AHD=∠B+∠HDB=2∠B,
∴∠B=∠HDB,
∴HB=HD=DC,
∴AC+CD=AH+BH=AB.
26.解:(1)如图1中,连接BB′.
由翻折的性质可知,∠DBE=∠DB′E=80°,
∵∠ADB′=∠DBB′+∠DB′B=125°,
∴∠EBB′+∠EB′B=160°﹣125°=35°,
∴∠CEB′=∠EBB′+∠EB′B=35°.
(2)结论:∠CEB′=∠ADB′+20°.
理由:如图2中,
∵∠ADB′+∠BEB′=360°﹣2×(180°﹣80°),
∴∠ADB′+180°﹣∠CEB′=160°,
∴∠CEB′=∠ADB′+20°.
(3)如图1﹣1中,当点D在线段AB上时,结论:∠CB′E+80°=∠ADB′
理由:连接CB′.
∵CB′∥AB,
∴∠ADB′=∠CB′D,
由翻折可知,∠B=∠DB′E=80°,
∴∠CB′E+80°=∠CB′D=∠ADB′.
如图2中,当点D在AB的延长线上时,结论:∠CB′E+∠ADB′=80°.
理由:连接CB′.
∵CB′∥AD,
∴∠ADB′+∠DB′C=180°,
∵∠ABC=80°,
∴∠DBE=∠DB′E=100°,
∴∠CB′E+100°+∠ADB′=180°,
∴∠CB′E+∠ADB′=80°.
综上所述,∠CB'E与∠ADB'的数量关系为∠CB′E+80°=∠ADB′或∠CB′E+∠ADB′=80°.
故答案为:∠CB′E+80°=∠ADB′或∠CB′E+∠ADB′=80°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
