6.2平行四边形的判定(第3课时)-2020-2021学年北师大版八年级数学下册课件(共18张ppt)
文档属性
| 名称 | 6.2平行四边形的判定(第3课时)-2020-2021学年北师大版八年级数学下册课件(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 930.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 21:18:48 | ||
图片预览






文档简介
北师大版数学八年级(下)
2.平行四边形的判定
第六章 平行四边形
第3课时 平行四边形性质及判定方法的综合应用
教学目标
00
重点难点
2.综合应用平行四边形的判定方法判定平行四边形.(难点)
1.理解并掌握平行线间的距离的概念并应用(重点)
答一答
教学过程
01
温故知新
1.平行四边形的定义是什么?
2.平行四边形有哪些性质?
3.平行四边形的判定方法有哪些?
议一议
教学过程
02
新课引入
在笔直轨道上,夹在两根铁轨之间的平行枕木一样长吗?你是怎样想的?与同伴交流。
证一证
教学过程
03
新知新授
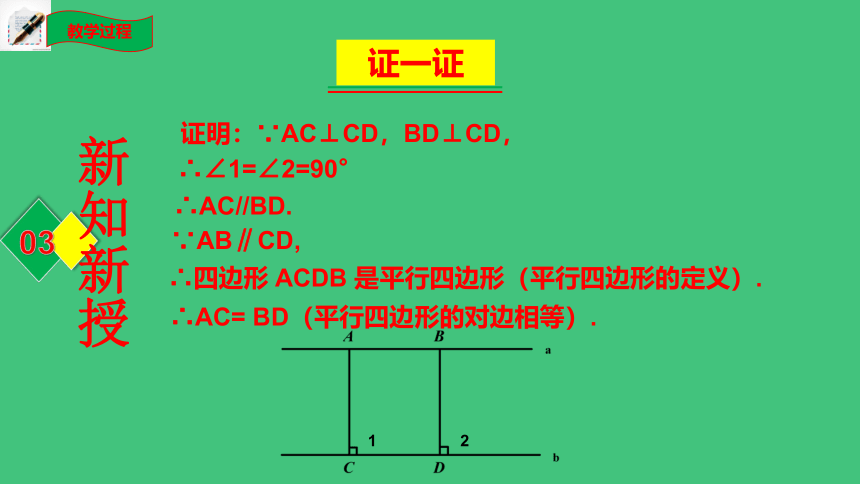
已知,如图,直线a∥b,A、B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别是C、D.
求证:AC=BD.
证一证
教学过程
03
新知新授
证明:∵AC⊥CD,BD⊥CD,
∴∠1=∠2=90°
∴AC//BD.
∵AB∥CD,
∴四边形 ACDB 是平行四边形(平行四边形的定义).
∴AC= BD(平行四边形的对边相等).
1
2
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等,这个距离称为平行线之间的距离.
记一记
教学过程
03
新知新授
平行线间的距离处处相等.
议一议
教学过程
03
新知新授
平行线间的距离处处相等,夹在平行线间的平行线短相等吗?
证一证
教学过程
03
新知新授
已知,如图,直线a∥b,A、B是直线a上的点,C、D是直线b上的点,且AC∥BD.
求证:AD=BC.
让学生口头完成证明
记一记
教学过程
03
新知新授
夹在平行线间的平行线短一定相等.
答一答
教学过程
04
新知应用
1.平行线之间的距离是指( )
A.从一条直线上一点到另一直线的垂线段
B.从一条直线上一点到另一条直线的垂线段长度
C.从一条直线上一点到另一条直线的垂线的长度
D.从一条直线上一点到另一条直线上的一点间线段的长度
2.如图,已知,a//b,AB//CD,CE⊥b于点E,FG⊥b于点 G,则下列说法中错误的是( )
A. AB = CD
B. CE = FG
C.A,B 两点间距离就是线段 AB 的长度
D.a与 b两平行线间的距离就是线段 CD 的长度
B
D
读一读
教学过程
05
回归课本
认真阅读课本第146页例4.
听一听
教学过程
06
例题解析
例. 在△ABC 中,AB=AC,点P为△ABC 内一点,过点P分别作 PF // AC 交 AB 于点 F,DE//AB交 BC 于点 D,交 AC 于点 E.
求证:PE+PF+PD=AB
证明:∵AB=AC,∴∠ B = ∠C,
听一听
教学过程
06
例题解析
∵DE//AB.
∴∠B = ∠CDE ,
∴∠C= ∠CDE,∴CE =ED= PD + PE
∵PF∥AC,PE// AB
∴四边形 PFAE 是平行四边形,
∴PF=AE,
∴PD +PE +PF=AB.
∵AE+ CE=AC
∴PD +PE +PF=AC.
做一做
教学过程
07
学以致用
例. 在△ABC 中,AB=AC,点P为△ABC 外一点,过点P分别作 PF // AC 交 AB 于点 F,PE//AB交 BC 于点 D,交 AC 于点 E.
求证:PE+PF-PD=AB
记一记
教学过程
08
课堂小结
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等,这个距离称为平行线之间的距离.
平行线间的距离处处相等.
夹在平行线间的平行线短一定相等.
做一做
教学过程
09
分层作业
第一层:课本第148页习题第1、2题.
第二层:课本第148页习题第1、2、3题.
教学过程
10
结束新课
感谢聆听
2.平行四边形的判定
第六章 平行四边形
第3课时 平行四边形性质及判定方法的综合应用
教学目标
00
重点难点
2.综合应用平行四边形的判定方法判定平行四边形.(难点)
1.理解并掌握平行线间的距离的概念并应用(重点)
答一答
教学过程
01
温故知新
1.平行四边形的定义是什么?
2.平行四边形有哪些性质?
3.平行四边形的判定方法有哪些?
议一议
教学过程
02
新课引入
在笔直轨道上,夹在两根铁轨之间的平行枕木一样长吗?你是怎样想的?与同伴交流。
证一证
教学过程
03
新知新授
已知,如图,直线a∥b,A、B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别是C、D.
求证:AC=BD.
证一证
教学过程
03
新知新授
证明:∵AC⊥CD,BD⊥CD,
∴∠1=∠2=90°
∴AC//BD.
∵AB∥CD,
∴四边形 ACDB 是平行四边形(平行四边形的定义).
∴AC= BD(平行四边形的对边相等).
1
2
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等,这个距离称为平行线之间的距离.
记一记
教学过程
03
新知新授
平行线间的距离处处相等.
议一议
教学过程
03
新知新授
平行线间的距离处处相等,夹在平行线间的平行线短相等吗?
证一证
教学过程
03
新知新授
已知,如图,直线a∥b,A、B是直线a上的点,C、D是直线b上的点,且AC∥BD.
求证:AD=BC.
让学生口头完成证明
记一记
教学过程
03
新知新授
夹在平行线间的平行线短一定相等.
答一答
教学过程
04
新知应用
1.平行线之间的距离是指( )
A.从一条直线上一点到另一直线的垂线段
B.从一条直线上一点到另一条直线的垂线段长度
C.从一条直线上一点到另一条直线的垂线的长度
D.从一条直线上一点到另一条直线上的一点间线段的长度
2.如图,已知,a//b,AB//CD,CE⊥b于点E,FG⊥b于点 G,则下列说法中错误的是( )
A. AB = CD
B. CE = FG
C.A,B 两点间距离就是线段 AB 的长度
D.a与 b两平行线间的距离就是线段 CD 的长度
B
D
读一读
教学过程
05
回归课本
认真阅读课本第146页例4.
听一听
教学过程
06
例题解析
例. 在△ABC 中,AB=AC,点P为△ABC 内一点,过点P分别作 PF // AC 交 AB 于点 F,DE//AB交 BC 于点 D,交 AC 于点 E.
求证:PE+PF+PD=AB
证明:∵AB=AC,∴∠ B = ∠C,
听一听
教学过程
06
例题解析
∵DE//AB.
∴∠B = ∠CDE ,
∴∠C= ∠CDE,∴CE =ED= PD + PE
∵PF∥AC,PE// AB
∴四边形 PFAE 是平行四边形,
∴PF=AE,
∴PD +PE +PF=AB.
∵AE+ CE=AC
∴PD +PE +PF=AC.
做一做
教学过程
07
学以致用
例. 在△ABC 中,AB=AC,点P为△ABC 外一点,过点P分别作 PF // AC 交 AB 于点 F,PE//AB交 BC 于点 D,交 AC 于点 E.
求证:PE+PF-PD=AB
记一记
教学过程
08
课堂小结
如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等,这个距离称为平行线之间的距离.
平行线间的距离处处相等.
夹在平行线间的平行线短一定相等.
做一做
教学过程
09
分层作业
第一层:课本第148页习题第1、2题.
第二层:课本第148页习题第1、2、3题.
教学过程
10
结束新课
感谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
