6.4多边形的内角和与外角和(第1课时)-2020-2021学年北师大版八年级数学下册课件(22张)
文档属性
| 名称 | 6.4多边形的内角和与外角和(第1课时)-2020-2021学年北师大版八年级数学下册课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 835.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 13:38:34 | ||
图片预览







文档简介
北师大版数学八年级(下)
4.多边形的内角和与外角和
第六章 平行四边形
第1课时 多边形的内角和
教学目标
00
重点难点
2.利用多边形的内角和定理解决问题.(难点)
1.理解并掌握多边形的内角和定理及其推导过程(重点)
答一答
教学过程
01
温故知新
1.什么是多边形?
2.从多边形的一个顶点出发的线段可以将多边形分成多少个三角形?
3.三角形的内角和是多少?
议一议
教学过程
02
新课引入
上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗?与同伴交流.
做一做
教学过程
03
新知新授
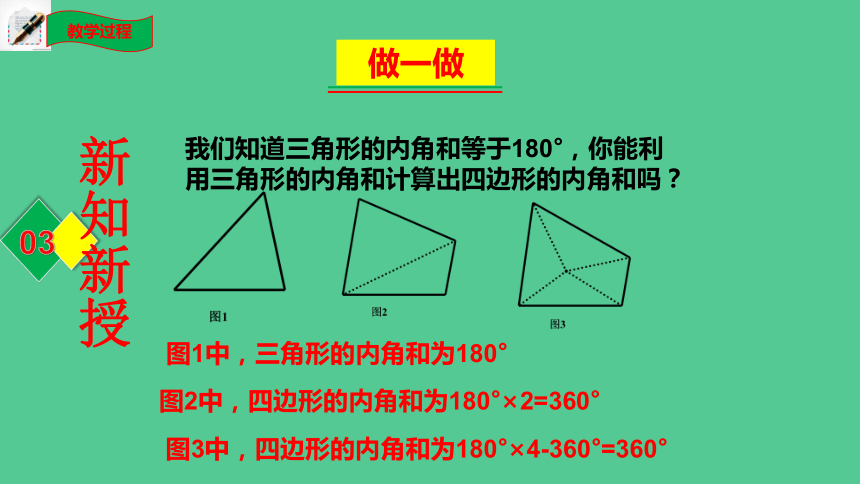
我们知道三角形的内角和等于180°,你能利用三角形的内角和计算出四边形的内角和吗?
图1中,三角形的内角和为180°
图2中,四边形的内角和为180°×2=360°
图3中,四边形的内角和为180°×4-360°=360°
做一做
教学过程
03
新知新授
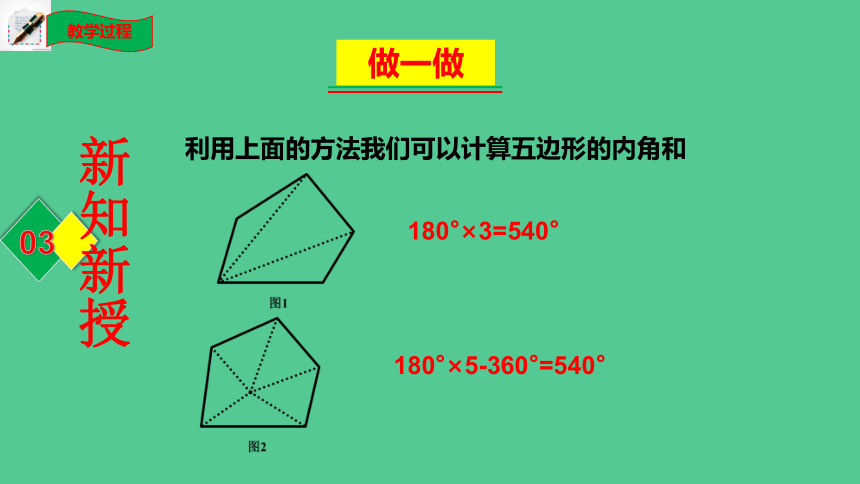
利用上面的方法我们可以计算五边形的内角和
180°×3=540°
180°×5-360°=540°
议一议
教学过程
03
新知新授
利用上面的方法你可以计算六边形、七边形、八边形……n边形的内角和吗?与同伴交流.
记一记
教学过程
03
新知新授
通过上面的探究,我们得出多边形的内角和定理.
定理 n多边形的内角和等于(n-2)·180°.
做一做
教学过程
04
新知应用
1.六边形的内角和是( )
A.540° B. 720° C.900° D.360°
2.一个多边形的内角和是900°,这个多边形的边数是( )
A.4 B.5 C.6 D.7
3.如果从某个多边形的一个顶点出发的对角线共有3 条,那么该多边形的内角和是 度.
B
D
720°
读一读
教学过程
05
回归课本
认真阅读课本第153页例1,体会多边形内角和定理在解题中的应用. 从本例题中你能总结出什么有用的结论?
记一记
教学过程
05
回归课本
从本例题中你能总结出什么有用的结论?
如果四边形的一组对角互补,那么另一组对角也互补.
对角互补的四边形的一个外角等于它的内对角.
如果∠A+∠C=180°,那么∠B+∠D=180°
如果∠A+∠C=180°或∠B+∠D=180°,那么∠1=∠B
议一议
教学过程
06
新知拓展
怎样计算正多边形各内角的度数?
先计算正三角形、正四边形、正五边形、正六边形、正八边形等多边形的内角和.
算一算
教学过程
06
新知拓展
正三角形内角和=180°;每个内角=180°÷3=60°
正四边形内角和=360°;每个内角=360°÷4=90°
正五边形内角和=540°;每个内角=540°÷5=108°
正六边形内角和=720°;每个内角=720°÷6=120°
正八边形内角和=1080°;每个内角=1080°÷8=135°
记一记
教学过程
06
新知拓展
计算正n边形各内角的度数?
议一议
教学过程
07
思维拓展
剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
议一议
教学过程
07
思维拓展
长方形纸片的一个角后,有三种情况.
内角和:180°
内角和:360°
内角和:540°
n边形减掉一个角后,有几种情况?内角和等于多少?
听一听
教学过程
08
例题解析
例.小明想设计一个内角和为 2 008°的多边形图案,请问小明的想法能实现吗?
解:小明的想法不能实现.
∵多边形内角和为(n -2)×180°,一定是 180 的整数倍,而2 008 不能被 180 整除,
∴不可能有内角和为 2 008°的多边形。
听一听
教学过程
08
例题解析
做一做
教学过程
09
学以致用
完成课本154页“随堂练习”
记一记
教学过程
10
课堂小结
定理 n多边形的内角和等于(n-2)·180°.
如果四边形的一组对角互补,那么另一组对角也互补.
对角互补的四边形的一个外角等于它的内对角.
分层作业
教学过程
11
课后巩固
第一层:第155页习题1、2题.
第二层:第155页习题1、2、3题.
教学过程
12
结束新课
感谢聆听
4.多边形的内角和与外角和
第六章 平行四边形
第1课时 多边形的内角和
教学目标
00
重点难点
2.利用多边形的内角和定理解决问题.(难点)
1.理解并掌握多边形的内角和定理及其推导过程(重点)
答一答
教学过程
01
温故知新
1.什么是多边形?
2.从多边形的一个顶点出发的线段可以将多边形分成多少个三角形?
3.三角形的内角和是多少?
议一议
教学过程
02
新课引入
上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗?与同伴交流.
做一做
教学过程
03
新知新授
我们知道三角形的内角和等于180°,你能利用三角形的内角和计算出四边形的内角和吗?
图1中,三角形的内角和为180°
图2中,四边形的内角和为180°×2=360°
图3中,四边形的内角和为180°×4-360°=360°
做一做
教学过程
03
新知新授
利用上面的方法我们可以计算五边形的内角和
180°×3=540°
180°×5-360°=540°
议一议
教学过程
03
新知新授
利用上面的方法你可以计算六边形、七边形、八边形……n边形的内角和吗?与同伴交流.
记一记
教学过程
03
新知新授
通过上面的探究,我们得出多边形的内角和定理.
定理 n多边形的内角和等于(n-2)·180°.
做一做
教学过程
04
新知应用
1.六边形的内角和是( )
A.540° B. 720° C.900° D.360°
2.一个多边形的内角和是900°,这个多边形的边数是( )
A.4 B.5 C.6 D.7
3.如果从某个多边形的一个顶点出发的对角线共有3 条,那么该多边形的内角和是 度.
B
D
720°
读一读
教学过程
05
回归课本
认真阅读课本第153页例1,体会多边形内角和定理在解题中的应用. 从本例题中你能总结出什么有用的结论?
记一记
教学过程
05
回归课本
从本例题中你能总结出什么有用的结论?
如果四边形的一组对角互补,那么另一组对角也互补.
对角互补的四边形的一个外角等于它的内对角.
如果∠A+∠C=180°,那么∠B+∠D=180°
如果∠A+∠C=180°或∠B+∠D=180°,那么∠1=∠B
议一议
教学过程
06
新知拓展
怎样计算正多边形各内角的度数?
先计算正三角形、正四边形、正五边形、正六边形、正八边形等多边形的内角和.
算一算
教学过程
06
新知拓展
正三角形内角和=180°;每个内角=180°÷3=60°
正四边形内角和=360°;每个内角=360°÷4=90°
正五边形内角和=540°;每个内角=540°÷5=108°
正六边形内角和=720°;每个内角=720°÷6=120°
正八边形内角和=1080°;每个内角=1080°÷8=135°
记一记
教学过程
06
新知拓展
计算正n边形各内角的度数?
议一议
教学过程
07
思维拓展
剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
议一议
教学过程
07
思维拓展
长方形纸片的一个角后,有三种情况.
内角和:180°
内角和:360°
内角和:540°
n边形减掉一个角后,有几种情况?内角和等于多少?
听一听
教学过程
08
例题解析
例.小明想设计一个内角和为 2 008°的多边形图案,请问小明的想法能实现吗?
解:小明的想法不能实现.
∵多边形内角和为(n -2)×180°,一定是 180 的整数倍,而2 008 不能被 180 整除,
∴不可能有内角和为 2 008°的多边形。
听一听
教学过程
08
例题解析
做一做
教学过程
09
学以致用
完成课本154页“随堂练习”
记一记
教学过程
10
课堂小结
定理 n多边形的内角和等于(n-2)·180°.
如果四边形的一组对角互补,那么另一组对角也互补.
对角互补的四边形的一个外角等于它的内对角.
分层作业
教学过程
11
课后巩固
第一层:第155页习题1、2题.
第二层:第155页习题1、2、3题.
教学过程
12
结束新课
感谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
