19.2.2待定系数法求一次函数解析式 课件-2020-2021学年人教版八年级数学下册(26张)
文档属性
| 名称 | 19.2.2待定系数法求一次函数解析式 课件-2020-2021学年人教版八年级数学下册(26张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 13:41:33 | ||
图片预览







文档简介
空白演示
单击输入您的封面副标题
19.2.2用待定系数法一次函数解析式
人教 版八年级数学下册
已知正比例函数的图象经过点(-2,4).
求这个正比例函数的解析式.
解:
∵y=kx的图象过点 (-2,4),
∴ 4=-2k
解得 k=-2
∴这个一次函数的解析式为y=-2x
温故知新
例1:已知正比例函数的图象经过点(-2,4).
求这个正比例函数的解析式.
∵y=kx的图象过点 (-2,4),
∴ 4=-2k
解得 k=-2
∴这个一次函数的解析式为y=-2x .
设
代
求
写
解:设这个一次函数的解析式为y=kx.
先设出函数解析式,再根据条件列出方程或方程组,求出未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
探究新知
例2.已知一次函数y=kx+b 的图象 与y=2x平行且过点(2,-1).求这个一次函数的解析式.
解:
∵ y=kx+b 的图象与y=2x平行.
∴ -1=2×2 +b
解得 b=-5
∴这个一次函数的解析式为y=2x-5
∵ y=2x+b 的图象过点(2,-1).
∴ k=2
∴ y=2x+b
探究新知
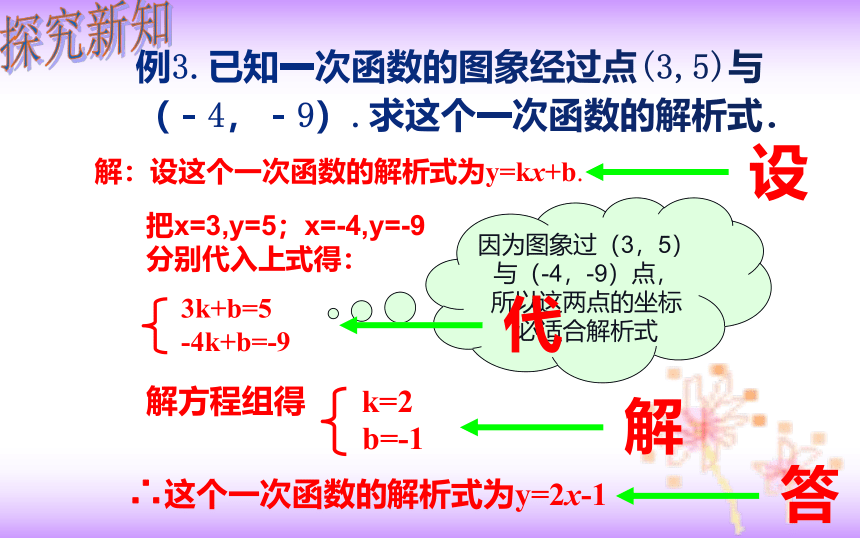
例3.已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
3k+b=5
-4k+b=-9
解方程组得 k=2
b=-1
∴这个一次函数的解析式为y=2x-1
因为图象过(3,5)与(-4,-9)点,所以这两点的坐标必适合解析式
把x=3,y=5;x=-4,y=-9分别代入上式得:
设
代
解
答
探究新知
思路:求一次函数的表达式
求k、b的值
列二元一次方程组
解方程组
用待定系数法求一次函数解析式的基本步骤
找两点坐标 设 代 解 答
探究新知
(一)根据已知条件,求函数解析式
已知一次函数y=kx+b,当x=1时,y=1,当x=2时,y=3.求这个一次函数的解析式.
解:
∴ k+b=1
2k+b=3
解得 k=2
b=-1
∴这个一次函数的解析式为y=2x-1
∵当x=1时,y=1,当x=2时,y=3.
探究新知
小明根据某个一次函数关系式填写了下表:
x
-1
0
1
y
2
4
其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。
∴ b=2
k+b=4
∴y=2x+2∴x=-1时y=0
∵当x=0时,y=1,当x=1时,y=0.
∴ k=2
b=2
解:设这个一次函数的解析式为y=kx+b.
练一练
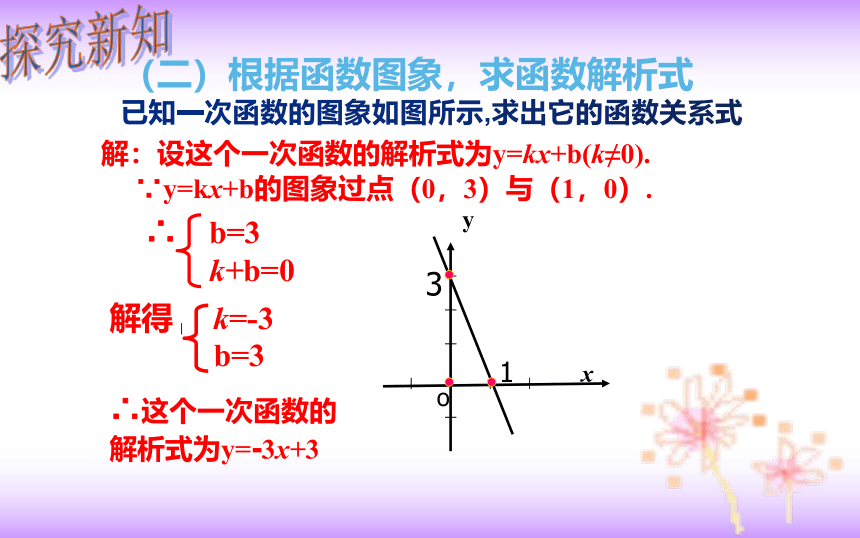
(二)根据函数图象,求函数解析式
已知一次函数的图象如图所示,求出它的函数关系式
3
1
o
解:设这个一次函数的解析式为y=kx+b(k≠0).
∴ b=3
k+b=0
解得 k=-3
b=3
∴这个一次函数的
解析式为y=-3x+3
y
x
∵y=kx+b的图象过点(0,3)与(1,0).
探究新知
(三)求函数解析式的综合应用
如图,一次函数y=kx+b 的图象过点A(3,0).与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式
解:∵y=kx+b的图象过点A(3,0).
∴OA=3,S= OA×OB= ×3×OB=6
∴OB=4, B点的坐标为(0,4),
则 y=kx+4
∴ 0=3k+4, ∴k= -
∴ y= - x+4
探究新知
解:设一次函数的解析式为y=kx+b(k≠0)
∵一次函数y=kx+b的图象过点(0,2),
∴b=2
∵一次函数的图象与x轴的交点是( ,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
练一练
(四)与求函数解析式有关的实际应用题
某摩托车油箱最多可存油5升,行驶时油箱的余油量y(升)与行驶的路程x(千米)成一次函数的关系,其图象如图所示:
(1)求y与x的函数关系式;
(2)摩托车加满油后,最多能行驶多少千米
0
60
x(千米)
y(升)
5
3
A
B
解:(1) 设y=kx+b(k≠0)
当x=0时,y=5,∴ b=5.
当x=60时,y=3,∴ 60k+5=3.
∴ k=-1/30
(2) 把y=0代入函数关系式,得
-1/30·x+5=0
故摩托车加满油后,最多能行驶150千米.
探究新知
已知弹簧长度y(厘米)在一定限度内所挂重物质量x(千克)的一次函数,现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的解析式。
解:设这个一次函数的解析式为:y=kx+b
所以一次函数的解析式为:y=0.3x+6
根据题意,把x=0,y=6和x=4,y=7.2代入,得:
解得
b=6
4k+b=7.2
b=6
k=0.3
练一练
1. 已知一次函数 ,
当
时,
y的值为4, 求k的值.
解:把x=5,y=4代入y=kx+2得:4=5k+2,解得 k=
巩固练习
2、若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( )
A(-1,1) B (2,2)
C(-2,2) D (2,一2)
B
巩固练习
3.已知直线 y=kx+b 经过点(9,0)和
点(24,20),求函数解析式.
把x=9,y=0和x=24,y=20分别代入y=kx+b得:
解:
20=24k+b
0=9k+b
解方程组得:
K=
b=-12
这个一次函数的解析式为
巩固练习
4.已知一次函数y=kx+b 的图象过点A(3,0).与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式.
巩固练习
∵y=kx+b的图象过点A(3,0).
∴OA=3,S= OA×OB= ×3×OB=6
∴OB=4, ∴B点的坐标为(0,4) (0,-4).
当B点的坐标为(0,4)时,则 y=kx+4
当B点的坐标为(0,-4)时,则 y=kx-4
∴ 0=3k+4, ∴k= - ∴ y= - x+4
∴ 0=3k+4, ∴k= ∴ y= x-4
∴一次函数解析式 y= - x+4 或 y= x-4
巩固练习
5.正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
分析:由OB=5可知点B的坐标为(0,-5).
y=k1x的图象过点A(3,4),y=k2x+b的图象过点A(3,4),B(0,-5),代入解方程(组)即可.
巩固练习
6.某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如下所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作几小时?
巩固练习
解这个方程组,得
所以 y = -5x + 40.
(1)求y关于x的函数表达式;
解
: 设一次函数的表达式为y = kx + b ,由于
点P (2,30), Q(6,10)都在一次
函数图象上,将这两点坐标代入表达式,得
2k + b =30,
6k + b =10.
{
巩固练习
解: 当剩余油量为0时, 即y=0 时,
有 -5x + 40 = 0,
解得 x = 8.
所以一箱油可供拖拉机工作8 h.
(2)一箱油可供拖拉机工作几小时?
巩固练习
7.一次函数y=kx+b(k≠0)的自变量的取值范围是-3≤x≤6,相应函数值的范围是-5≤y≤-2,求这个函数的解析式.
由于此题中没有明确k的正负,且一次函数y=kx+b(k≠0)只有在k>0时,y随x的增大而增大,在k<0时,y随x的增大而减小,故此题要分k>0和k<0两种情况进行讨论。
巩固练习
用待定系数法求一次函数的解析式
2. 根据已知条件列出关于k,b的方程(组);
1. 设所求的一次函数解析式为y=kx+b;
3. 解方程,求出k,b;
4. 把求出的k,b代回解析式即可.
课堂小结
布置作业
教科书99页,习题 19.2 ,7,8题
教科书第60页第3、6题
布置作业
再见
单击输入您的封面副标题
19.2.2用待定系数法一次函数解析式
人教 版八年级数学下册
已知正比例函数的图象经过点(-2,4).
求这个正比例函数的解析式.
解:
∵y=kx的图象过点 (-2,4),
∴ 4=-2k
解得 k=-2
∴这个一次函数的解析式为y=-2x
温故知新
例1:已知正比例函数的图象经过点(-2,4).
求这个正比例函数的解析式.
∵y=kx的图象过点 (-2,4),
∴ 4=-2k
解得 k=-2
∴这个一次函数的解析式为y=-2x .
设
代
求
写
解:设这个一次函数的解析式为y=kx.
先设出函数解析式,再根据条件列出方程或方程组,求出未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
探究新知
例2.已知一次函数y=kx+b 的图象 与y=2x平行且过点(2,-1).求这个一次函数的解析式.
解:
∵ y=kx+b 的图象与y=2x平行.
∴ -1=2×2 +b
解得 b=-5
∴这个一次函数的解析式为y=2x-5
∵ y=2x+b 的图象过点(2,-1).
∴ k=2
∴ y=2x+b
探究新知
例3.已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
3k+b=5
-4k+b=-9
解方程组得 k=2
b=-1
∴这个一次函数的解析式为y=2x-1
因为图象过(3,5)与(-4,-9)点,所以这两点的坐标必适合解析式
把x=3,y=5;x=-4,y=-9分别代入上式得:
设
代
解
答
探究新知
思路:求一次函数的表达式
求k、b的值
列二元一次方程组
解方程组
用待定系数法求一次函数解析式的基本步骤
找两点坐标 设 代 解 答
探究新知
(一)根据已知条件,求函数解析式
已知一次函数y=kx+b,当x=1时,y=1,当x=2时,y=3.求这个一次函数的解析式.
解:
∴ k+b=1
2k+b=3
解得 k=2
b=-1
∴这个一次函数的解析式为y=2x-1
∵当x=1时,y=1,当x=2时,y=3.
探究新知
小明根据某个一次函数关系式填写了下表:
x
-1
0
1
y
2
4
其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。
∴ b=2
k+b=4
∴y=2x+2∴x=-1时y=0
∵当x=0时,y=1,当x=1时,y=0.
∴ k=2
b=2
解:设这个一次函数的解析式为y=kx+b.
练一练
(二)根据函数图象,求函数解析式
已知一次函数的图象如图所示,求出它的函数关系式
3
1
o
解:设这个一次函数的解析式为y=kx+b(k≠0).
∴ b=3
k+b=0
解得 k=-3
b=3
∴这个一次函数的
解析式为y=-3x+3
y
x
∵y=kx+b的图象过点(0,3)与(1,0).
探究新知
(三)求函数解析式的综合应用
如图,一次函数y=kx+b 的图象过点A(3,0).与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式
解:∵y=kx+b的图象过点A(3,0).
∴OA=3,S= OA×OB= ×3×OB=6
∴OB=4, B点的坐标为(0,4),
则 y=kx+4
∴ 0=3k+4, ∴k= -
∴ y= - x+4
探究新知
解:设一次函数的解析式为y=kx+b(k≠0)
∵一次函数y=kx+b的图象过点(0,2),
∴b=2
∵一次函数的图象与x轴的交点是( ,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
练一练
(四)与求函数解析式有关的实际应用题
某摩托车油箱最多可存油5升,行驶时油箱的余油量y(升)与行驶的路程x(千米)成一次函数的关系,其图象如图所示:
(1)求y与x的函数关系式;
(2)摩托车加满油后,最多能行驶多少千米
0
60
x(千米)
y(升)
5
3
A
B
解:(1) 设y=kx+b(k≠0)
当x=0时,y=5,∴ b=5.
当x=60时,y=3,∴ 60k+5=3.
∴ k=-1/30
(2) 把y=0代入函数关系式,得
-1/30·x+5=0
故摩托车加满油后,最多能行驶150千米.
探究新知
已知弹簧长度y(厘米)在一定限度内所挂重物质量x(千克)的一次函数,现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的解析式。
解:设这个一次函数的解析式为:y=kx+b
所以一次函数的解析式为:y=0.3x+6
根据题意,把x=0,y=6和x=4,y=7.2代入,得:
解得
b=6
4k+b=7.2
b=6
k=0.3
练一练
1. 已知一次函数 ,
当
时,
y的值为4, 求k的值.
解:把x=5,y=4代入y=kx+2得:4=5k+2,解得 k=
巩固练习
2、若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( )
A(-1,1) B (2,2)
C(-2,2) D (2,一2)
B
巩固练习
3.已知直线 y=kx+b 经过点(9,0)和
点(24,20),求函数解析式.
把x=9,y=0和x=24,y=20分别代入y=kx+b得:
解:
20=24k+b
0=9k+b
解方程组得:
K=
b=-12
这个一次函数的解析式为
巩固练习
4.已知一次函数y=kx+b 的图象过点A(3,0).与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式.
巩固练习
∵y=kx+b的图象过点A(3,0).
∴OA=3,S= OA×OB= ×3×OB=6
∴OB=4, ∴B点的坐标为(0,4) (0,-4).
当B点的坐标为(0,4)时,则 y=kx+4
当B点的坐标为(0,-4)时,则 y=kx-4
∴ 0=3k+4, ∴k= - ∴ y= - x+4
∴ 0=3k+4, ∴k= ∴ y= x-4
∴一次函数解析式 y= - x+4 或 y= x-4
巩固练习
5.正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
分析:由OB=5可知点B的坐标为(0,-5).
y=k1x的图象过点A(3,4),y=k2x+b的图象过点A(3,4),B(0,-5),代入解方程(组)即可.
巩固练习
6.某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如下所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作几小时?
巩固练习
解这个方程组,得
所以 y = -5x + 40.
(1)求y关于x的函数表达式;
解
: 设一次函数的表达式为y = kx + b ,由于
点P (2,30), Q(6,10)都在一次
函数图象上,将这两点坐标代入表达式,得
2k + b =30,
6k + b =10.
{
巩固练习
解: 当剩余油量为0时, 即y=0 时,
有 -5x + 40 = 0,
解得 x = 8.
所以一箱油可供拖拉机工作8 h.
(2)一箱油可供拖拉机工作几小时?
巩固练习
7.一次函数y=kx+b(k≠0)的自变量的取值范围是-3≤x≤6,相应函数值的范围是-5≤y≤-2,求这个函数的解析式.
由于此题中没有明确k的正负,且一次函数y=kx+b(k≠0)只有在k>0时,y随x的增大而增大,在k<0时,y随x的增大而减小,故此题要分k>0和k<0两种情况进行讨论。
巩固练习
用待定系数法求一次函数的解析式
2. 根据已知条件列出关于k,b的方程(组);
1. 设所求的一次函数解析式为y=kx+b;
3. 解方程,求出k,b;
4. 把求出的k,b代回解析式即可.
课堂小结
布置作业
教科书99页,习题 19.2 ,7,8题
教科书第60页第3、6题
布置作业
再见
