19.2.2一次函数 课件-2020-2021学年人教版八年级数学下册(19张)
文档属性
| 名称 | 19.2.2一次函数 课件-2020-2021学年人教版八年级数学下册(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 762.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 13:42:20 | ||
图片预览






文档简介
空白演示
单击输入您的封面副标题
19.2.2一次函数
人教 版八年级数学下册
k>0
k<0
x
y
0
x
y
0
一、三象限
二、四象限
y随x的增大而减小
y随x的增大而增大
图像必经过(0,0)和(1,k)这两个点
正比例函数y=kx(k是常数,k≠0) 的图像和性质
k的正负性
y=kx(k是常数,
k≠0)的图像
直线y=kx经过
的象限
性质
图像必经过的点
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
温故知新
某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃ ,登山队员由大本营向上登高xkm时,他们所在位置的气温是y℃.
(1)试用解析式表示y与x的关系.
解:y与x的函数关系式为
y=5-6x
这个函数关系式也可以写为
y=-6x+5
(2)当登山队员由大本营向上登高0.5km时他们所在位置的气温是多少?
解:当x=0.5时,y=-6×0.5+5=2℃
新课导入
下列问题中的变量对应关系可用怎样的函数表示?
(1)有人发现,在20-25 ℃的蟋蟀每分钟名叫次数c与温度t(单位:℃ )有关即c的值约是t的七倍与35的差;
解: c=7t-35
(2)一种计算成年人标准体重G(单位:千克)的方法是,以厘米为单位量出身高值h减常数105,所得差是G的值;
解:G=h-105
探究新知
(3)某城市的市内电话的月收费额y(单位:元)包括:月租费22元,拨打电话x分钟的计时费按0.01元/分钟收取;
解:y=0.01x+22
(4)把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的值而变化.
解:y=-5x+50
探究新知
函数解析式
常数
自变量
函数
(1)c=7t-35
(2)G=h-105
(3)y=0.01x+22
(4)y=-5x+50
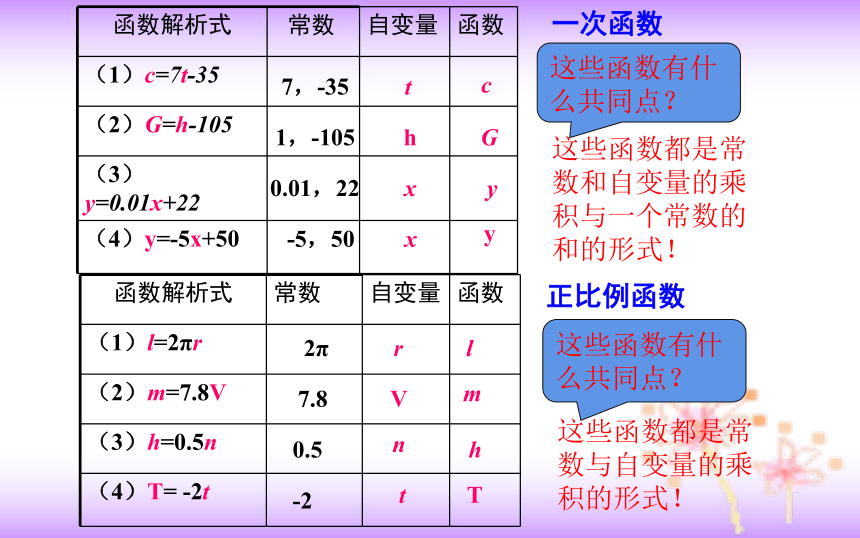
这些函数有什么共同点?
这些函数都是常数和自变量的乘积与一个常数的和的形式!
7,-35
t
c
1,-105
h
G
0.01,22
x
y
-5,50
x
y
函数解析式
常数
自变量
函数
(1)l=2πr
(2)m=7.8V
(3)h=0.5n
(4)T= -2t
2π
r
l
7.8
V
m
0.5
n
h
-2
t
T
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式!
正比例函数
一次函数
一般地,形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数。
(1) k≠0 .
(2)x 的次数是1.
(3)常数项b可以为一切实数.
思考:一次函数的结构特征有哪些?
一次函数
正比例函数
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数。
探究新知
例1. 下列函数关系式中,哪些是一次函数,哪些是正比例函数?
它是一次函数,不是正比例函数。
它不是一次函数,也不是正比例函数。
它是一次函数,也是正比例函数。
它不是一次函数,也不是正比例函数。
它是一次函数,也是正比例函数。
(1)y=-x-4
(2)y=5x2+6
(3)y=2πx
(5)y=-8x
(4)
例题讲解
(3)当x=2.5时,y=3×2.5-9=-1.5.
例 2 。已知y与x-3成正比例,当x=4时,y=3.
(1)写出y与x之间的函数关系式;
(2)y与x之间是什么函数关系;
(3)求x=2.5时,y的值.
解 :
(1)因为 y与x-3成正比例,所以y=k(x-3).又因为x=4时,y=3,所以3= k(4-3),解得k=3,所以y=3(x-3)=3x-9.
(2) y是x的一次函数.
例题讲解
例3.已知函数y=(2-m)x+2m-3.求当m为何值时,
(1)此函数为一次函数;
(2) 此函数为正比例函数。
解:(1)由题意得, k = 2-m≠0, m≠2,所以m≠2时,此函数为一次函数。
(2)由题意, k = 2-m≠0, 解得,m≠2,
又因为b = 2m-3= 0, 解得,m=
所以当 m= 时,函数为正比例函数y= x。
例题讲解
D
(A )1个
( B)2个
( C)3个
( D)4个
2、下列说法不正确的是( )
(A)一次函数不一定是正比例函数
(B)不是一次函数就一定不是正比例函数
(C)正比例函数是特殊的一次函数
(D)不是正比例函数就不是一次函数
1、已知下列函数: y = 2x + 1;
; s = 60 t , 其中表示一次函数的有( )
x
y
8
=
y =100 - 25x
C
巩固练习
c
c
3.下列说法正确的是(??? )
A. 是一次函数?????
B.一次函数是正比例函数
C.正比例函数是一次函数???? ?
D.不是正比例函数就一定不是一次函数
4.下列函数中,不是一次函数的是( )
A. B.
C. D.
巩固练习
n=4
m≠3
≠2
= 2
(3) 要使y=(m-3)xn-3+1是关于x的一次函数, m, n应满足 , .
5.(1)要使y=(m-2)x+1是关于x的一次函数,则m____;
(2)要使
是关于x的一次函数,则n ____.
m=±2
m=-2
巩固练习
解:
因为当x=1时,y=5;当x=-1时,y=1
所以
解得k=2,b=3.
7.一次函数 ,当x=1时,y=5;当x=-1时,y=1.求k和b的值.
巩固练习
解:小球速度v关于时间t的函数解析式为v=2t,是一次函数.
(2)求第2.5s时小球的速度.
解:当t=2.5时,v=2x2.5=5(m/s)
8.一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加2m/s.
(1)求小球速度v(单位: )关于时间t(单位:s)的函数解析式.它是一次函数吗?
巩固练习
9.一个弹簧不挂重物时长12cm,挂上重物后伸长的长度与所挂重物的质量成正比.如果挂上1kg的物体后,弹簧伸长2cm.求弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数解析式.
解:∵挂上1kg的物体后,弹簧伸长2cm,
∴挂上xkg的物体后,弹簧伸长2xcm,
∴弹簧总长y关于所挂物体质量x的函数解析式为 y=12+2x
巩固练习
归纳小结
y=kx+b
正比例函数
1、一般地,形如 (k,b是常数,
)的函数,叫做 函数.
2、一次函数都是 与 的积与
的和的形式.
3、 是一种特殊的一次函数.
自变量x
常数b
常数k
一次
课堂小结
布置作业
教科书99页,习题 19.2 ,3题
教科书第60页第3、6题
布置作业
再见
单击输入您的封面副标题
19.2.2一次函数
人教 版八年级数学下册
k>0
k<0
x
y
0
x
y
0
一、三象限
二、四象限
y随x的增大而减小
y随x的增大而增大
图像必经过(0,0)和(1,k)这两个点
正比例函数y=kx(k是常数,k≠0) 的图像和性质
k的正负性
y=kx(k是常数,
k≠0)的图像
直线y=kx经过
的象限
性质
图像必经过的点
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
温故知新
某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃ ,登山队员由大本营向上登高xkm时,他们所在位置的气温是y℃.
(1)试用解析式表示y与x的关系.
解:y与x的函数关系式为
y=5-6x
这个函数关系式也可以写为
y=-6x+5
(2)当登山队员由大本营向上登高0.5km时他们所在位置的气温是多少?
解:当x=0.5时,y=-6×0.5+5=2℃
新课导入
下列问题中的变量对应关系可用怎样的函数表示?
(1)有人发现,在20-25 ℃的蟋蟀每分钟名叫次数c与温度t(单位:℃ )有关即c的值约是t的七倍与35的差;
解: c=7t-35
(2)一种计算成年人标准体重G(单位:千克)的方法是,以厘米为单位量出身高值h减常数105,所得差是G的值;
解:G=h-105
探究新知
(3)某城市的市内电话的月收费额y(单位:元)包括:月租费22元,拨打电话x分钟的计时费按0.01元/分钟收取;
解:y=0.01x+22
(4)把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的值而变化.
解:y=-5x+50
探究新知
函数解析式
常数
自变量
函数
(1)c=7t-35
(2)G=h-105
(3)y=0.01x+22
(4)y=-5x+50
这些函数有什么共同点?
这些函数都是常数和自变量的乘积与一个常数的和的形式!
7,-35
t
c
1,-105
h
G
0.01,22
x
y
-5,50
x
y
函数解析式
常数
自变量
函数
(1)l=2πr
(2)m=7.8V
(3)h=0.5n
(4)T= -2t
2π
r
l
7.8
V
m
0.5
n
h
-2
t
T
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式!
正比例函数
一次函数
一般地,形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数。
(1) k≠0 .
(2)x 的次数是1.
(3)常数项b可以为一切实数.
思考:一次函数的结构特征有哪些?
一次函数
正比例函数
当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数。
探究新知
例1. 下列函数关系式中,哪些是一次函数,哪些是正比例函数?
它是一次函数,不是正比例函数。
它不是一次函数,也不是正比例函数。
它是一次函数,也是正比例函数。
它不是一次函数,也不是正比例函数。
它是一次函数,也是正比例函数。
(1)y=-x-4
(2)y=5x2+6
(3)y=2πx
(5)y=-8x
(4)
例题讲解
(3)当x=2.5时,y=3×2.5-9=-1.5.
例 2 。已知y与x-3成正比例,当x=4时,y=3.
(1)写出y与x之间的函数关系式;
(2)y与x之间是什么函数关系;
(3)求x=2.5时,y的值.
解 :
(1)因为 y与x-3成正比例,所以y=k(x-3).又因为x=4时,y=3,所以3= k(4-3),解得k=3,所以y=3(x-3)=3x-9.
(2) y是x的一次函数.
例题讲解
例3.已知函数y=(2-m)x+2m-3.求当m为何值时,
(1)此函数为一次函数;
(2) 此函数为正比例函数。
解:(1)由题意得, k = 2-m≠0, m≠2,所以m≠2时,此函数为一次函数。
(2)由题意, k = 2-m≠0, 解得,m≠2,
又因为b = 2m-3= 0, 解得,m=
所以当 m= 时,函数为正比例函数y= x。
例题讲解
D
(A )1个
( B)2个
( C)3个
( D)4个
2、下列说法不正确的是( )
(A)一次函数不一定是正比例函数
(B)不是一次函数就一定不是正比例函数
(C)正比例函数是特殊的一次函数
(D)不是正比例函数就不是一次函数
1、已知下列函数: y = 2x + 1;
; s = 60 t , 其中表示一次函数的有( )
x
y
8
=
y =100 - 25x
C
巩固练习
c
c
3.下列说法正确的是(??? )
A. 是一次函数?????
B.一次函数是正比例函数
C.正比例函数是一次函数???? ?
D.不是正比例函数就一定不是一次函数
4.下列函数中,不是一次函数的是( )
A. B.
C. D.
巩固练习
n=4
m≠3
≠2
= 2
(3) 要使y=(m-3)xn-3+1是关于x的一次函数, m, n应满足 , .
5.(1)要使y=(m-2)x+1是关于x的一次函数,则m____;
(2)要使
是关于x的一次函数,则n ____.
m=±2
m=-2
巩固练习
解:
因为当x=1时,y=5;当x=-1时,y=1
所以
解得k=2,b=3.
7.一次函数 ,当x=1时,y=5;当x=-1时,y=1.求k和b的值.
巩固练习
解:小球速度v关于时间t的函数解析式为v=2t,是一次函数.
(2)求第2.5s时小球的速度.
解:当t=2.5时,v=2x2.5=5(m/s)
8.一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加2m/s.
(1)求小球速度v(单位: )关于时间t(单位:s)的函数解析式.它是一次函数吗?
巩固练习
9.一个弹簧不挂重物时长12cm,挂上重物后伸长的长度与所挂重物的质量成正比.如果挂上1kg的物体后,弹簧伸长2cm.求弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数解析式.
解:∵挂上1kg的物体后,弹簧伸长2cm,
∴挂上xkg的物体后,弹簧伸长2xcm,
∴弹簧总长y关于所挂物体质量x的函数解析式为 y=12+2x
巩固练习
归纳小结
y=kx+b
正比例函数
1、一般地,形如 (k,b是常数,
)的函数,叫做 函数.
2、一次函数都是 与 的积与
的和的形式.
3、 是一种特殊的一次函数.
自变量x
常数b
常数k
一次
课堂小结
布置作业
教科书99页,习题 19.2 ,3题
教科书第60页第3、6题
布置作业
再见
