2020-2021学年八年级数学沪科版下册19.2《平行四边形的性质》说课课件 (共21张PPT)
文档属性
| 名称 | 2020-2021学年八年级数学沪科版下册19.2《平行四边形的性质》说课课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 00:00:00 | ||
图片预览





文档简介
19.2平行四边形的性质
说课
教法学法
教学目标
教材分析
教学重点难点
教学过程
学情分析
一、教材分析
教材的地位和作用
(1) 从学生的个性品质看;
(2) 从学生的学习成绩和学习能力看。
二、学情分析
。
1.了解平行四边形的定义及相关概念;理解并掌握平行四边形的性质,并能运用性质解决简单的计算和证明.
2.经历性质的探索、发现与证明的过程,培养学生的观察能力、动手能力、抽象概括及逻辑推理能力,渗透“转化”的数学思想.
3.通过探究学习,增强发现问题、分析问题、解决问题的意识;通过列举生活中的平行四边形,感受数学来源于生活,又应用于生活.
二、教学目标
(教学重点)
(教学难点)
激趣 引导 点拨法
三、教法学法设计
群学 独学 互学方式
预习展示、释疑解惑
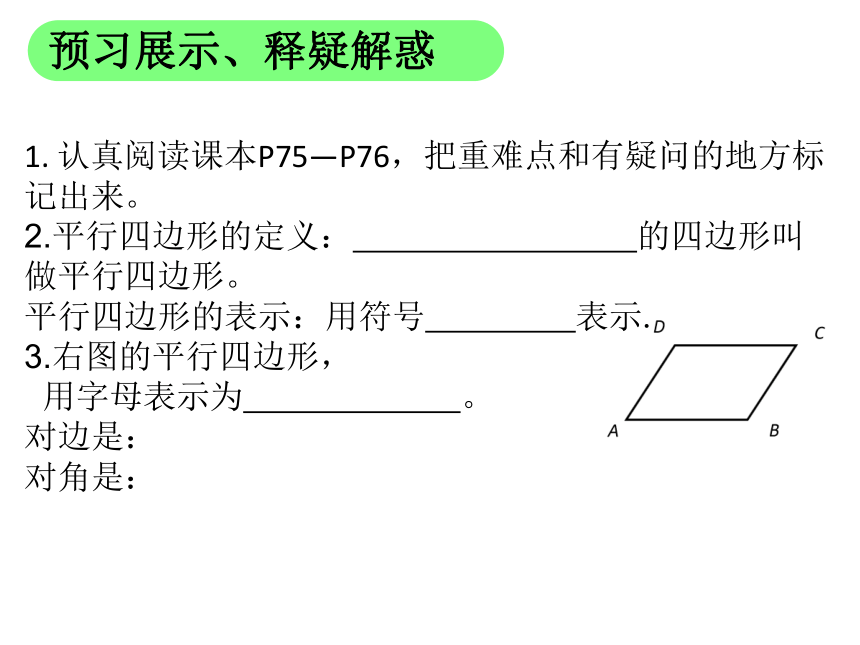
1. 认真阅读课本P75—P76,把重难点和有疑问的地方标记出来。
2.平行四边形的定义: 的四边形叫做平行四边形。
平行四边形的表示:用符号 表示.
3.右图的平行四边形,
用字母表示为 。
对边是:
对角是:
创设情境、引出概念
四、教学过程
反思小结,布置作业
尝试应用、巩固新知
动手操作、探究新知
激趣导入、引出课题
这是一个关于四边形家族的故事.....
很久很久以前,在一个四边形的世界里,到处都是四边形,大街小巷,无一不是四边形的身影。
有一天,在医院里生出了一个怪胎,突然生出了一组对边平行的四边形,他的父母十分无奈,便叫他“梯形”。
怪事时时都发生,有一个四边形,莫名奇妙,有一条腿就不见了,变成了三条腿,并且有两条腿是相等的,所以他父母叫她“等腰三角形
有一天,等腰三角形来到了梯形的国家,意外的遇见了梯形。他们一见钟情,不久就结婚了。
有一次,等腰梯形和他的朋友来到了一家伐木场玩耍。看见一个伐木机在运作,他好奇地走过去看,一不小心摔了一跤,机器的刀把他沿他的高正好切了开来,他哭着回到了家。父母看了心急如焚想:怎么办呢?等腰梯形残疾了,就只好叫他“直角梯形”
后来,他爱上了一个对角相等的姑娘,不久,他们结婚了生下了一个两组对边互相平行的孩子,夫妻两个就叫他“平行四边形”。
但是平行四边形太调皮了,有时把自己的邻边弄相等,哈哈大笑说:“哈哈,我现在变成菱形啦”
有时又故意把自己的角掰成 说:“哈哈,我现在变成矩形啦。
但是这样他觉得还不够,他竟然同时把自己的邻边弄相等,又把自己的角掰成 ,得意洋洋地说:“看看,我现在变成什么了呢?我现在是正方形啦!”
可是,有一天,平行四边形迷失了自我,忘记了自己有什么个性,所以,整日抑郁寡欢........
亲爱的同学们,你们可以帮帮平行四边形吗?帮帮它寻找自我,寻找属于它自己的特性.........
四边形家族的故事
(一)激趣导入
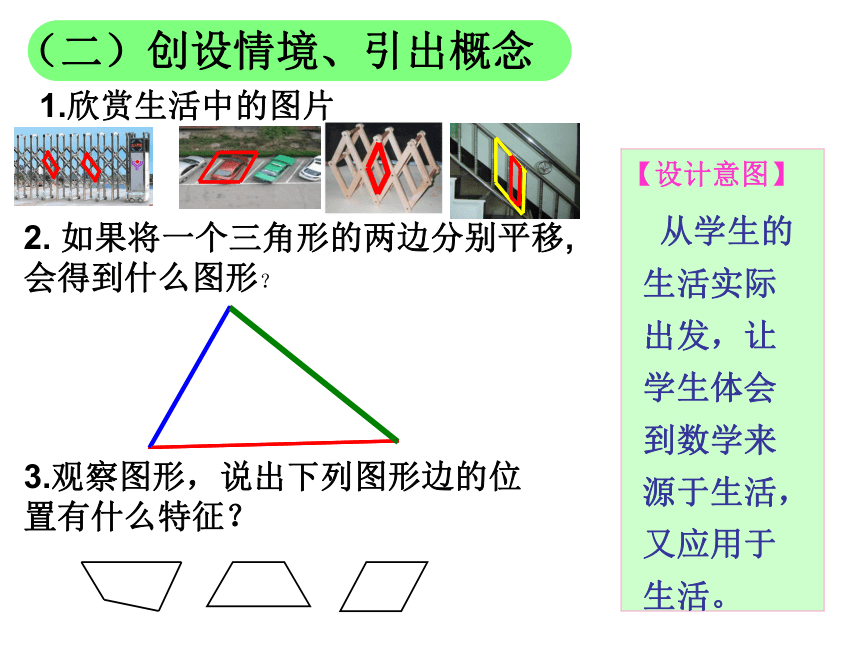
1.欣赏生活中的图片
(二)创设情境、引出概念
从学生的生活实际出发,让学生体会到数学来源于生活,又应用于生活。
【设计意图】
2. 如果将一个三角形的两边分别平移,会得到什么图形?
3.观察图形,说出下列图形边的位 置有什么特征?
1. 定义: 两组对边分别平行的四边形叫做平行四边形.
2.记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,
相对的角称为对角.
概念
活动 将两个全等的三角形纸片相等的边重合在一起,你能拼出平行四边形吗?你能拼出几个?与同学交流你的拼法,并把它展示出来.
说一说:通过拼图你可以得到什么结论?
平行四边形对边相等,对角相等,邻角互补.
一
这个结论正确吗?
(三)动手操作、探究新知
A
B
C
D
平行四边形问题
转化
三角形问题
证一证
证明:如图,连接AC,
∵AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA.
∴AB=CD,AD=BC,
∠B=∠D.
已知: ABCD,AB∥CD,AD∥BC.
求证: AB=CD,BC=DA;
∠B=∠D, ∠BAD=∠DCB
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3.
即∠BAD=∠DCB.
证明结论
平行四边形的性质
A
B
C
D
∵四边形ABCD是平行四边形 ∴AB=CD, AD=BC.
∠A=∠C,∠B=∠D.
∠A+∠B=180,∠A+∠D=180
性质1 平行四边形的对边相等.
性质2 平行四边形的对角相等、邻角互补.
得出结论
设计意图:培养学生的几何语言表达能力和逻辑推理能力。
1 .如图,在 ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______.
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
(四)尝试应用
典例精析
例1 已知:如图, ABCD中,BE平分∠ABC交于AD于点E.
(1) 如果AE=2,求CD的长;
(2)如果∠AEB=40?,求∠C的度数.
B
A
D
C
E
2. 已知: ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
B
A
D
C
E
F
A
D
B
C
E
F
1.已知:如图, ABCD中,BE平分∠ABC交于AD于点E,交CD的延长线于点F.
(1) 如果AE=2,BC=3,求DF的长;
(2)找出图中的等腰三角形.
00:12:29
本节课的交流学习你有哪
些收获呢?与大家分享一下
吧!
【学生活动】
我的收获是……
我感到最困惑的是……
今后我的学习打算是……
(五)反思小结
(六) 作业设计
1、必做题:教材78页练习1、2、3 题
2、选做题:学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
设计意图:针对学生个体差异进行分层训练,既使学生掌握基础知识,又达到“拔尖”和“减负”的目的;进一步弥补课堂中教与学的不足。
A1
A3
A2
A
B
C
平行四边形的性质
板书设计
性质2 平行四边形对角相等
2.性质
性质1 平行四边形对边相等
1.定义:
A
D
B
C
ABCD
记作:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
∴AB=CD AD=BC
∠A=∠C ∠B=∠D
∵四边形ABCD是平行四边形
几何语言
3.例题讲解:
教学反思
本节课根据学生的认知规律,本着激发兴趣,提高抽象概括和逻辑推理能力的原则设计的。由易到难,突破难点,突出重点,充分发挥学生的主体地位,使学生在自主探索,积极思考,合作交流的过程中掌握基础知识和基本技能,体会转化的数学思想,积累数学活动经验。
说课
教法学法
教学目标
教材分析
教学重点难点
教学过程
学情分析
一、教材分析
教材的地位和作用
(1) 从学生的个性品质看;
(2) 从学生的学习成绩和学习能力看。
二、学情分析
。
1.了解平行四边形的定义及相关概念;理解并掌握平行四边形的性质,并能运用性质解决简单的计算和证明.
2.经历性质的探索、发现与证明的过程,培养学生的观察能力、动手能力、抽象概括及逻辑推理能力,渗透“转化”的数学思想.
3.通过探究学习,增强发现问题、分析问题、解决问题的意识;通过列举生活中的平行四边形,感受数学来源于生活,又应用于生活.
二、教学目标
(教学重点)
(教学难点)
激趣 引导 点拨法
三、教法学法设计
群学 独学 互学方式
预习展示、释疑解惑
1. 认真阅读课本P75—P76,把重难点和有疑问的地方标记出来。
2.平行四边形的定义: 的四边形叫做平行四边形。
平行四边形的表示:用符号 表示.
3.右图的平行四边形,
用字母表示为 。
对边是:
对角是:
创设情境、引出概念
四、教学过程
反思小结,布置作业
尝试应用、巩固新知
动手操作、探究新知
激趣导入、引出课题
这是一个关于四边形家族的故事.....
很久很久以前,在一个四边形的世界里,到处都是四边形,大街小巷,无一不是四边形的身影。
有一天,在医院里生出了一个怪胎,突然生出了一组对边平行的四边形,他的父母十分无奈,便叫他“梯形”。
怪事时时都发生,有一个四边形,莫名奇妙,有一条腿就不见了,变成了三条腿,并且有两条腿是相等的,所以他父母叫她“等腰三角形
有一天,等腰三角形来到了梯形的国家,意外的遇见了梯形。他们一见钟情,不久就结婚了。
有一次,等腰梯形和他的朋友来到了一家伐木场玩耍。看见一个伐木机在运作,他好奇地走过去看,一不小心摔了一跤,机器的刀把他沿他的高正好切了开来,他哭着回到了家。父母看了心急如焚想:怎么办呢?等腰梯形残疾了,就只好叫他“直角梯形”
后来,他爱上了一个对角相等的姑娘,不久,他们结婚了生下了一个两组对边互相平行的孩子,夫妻两个就叫他“平行四边形”。
但是平行四边形太调皮了,有时把自己的邻边弄相等,哈哈大笑说:“哈哈,我现在变成菱形啦”
有时又故意把自己的角掰成 说:“哈哈,我现在变成矩形啦。
但是这样他觉得还不够,他竟然同时把自己的邻边弄相等,又把自己的角掰成 ,得意洋洋地说:“看看,我现在变成什么了呢?我现在是正方形啦!”
可是,有一天,平行四边形迷失了自我,忘记了自己有什么个性,所以,整日抑郁寡欢........
亲爱的同学们,你们可以帮帮平行四边形吗?帮帮它寻找自我,寻找属于它自己的特性.........
四边形家族的故事
(一)激趣导入
1.欣赏生活中的图片
(二)创设情境、引出概念
从学生的生活实际出发,让学生体会到数学来源于生活,又应用于生活。
【设计意图】
2. 如果将一个三角形的两边分别平移,会得到什么图形?
3.观察图形,说出下列图形边的位 置有什么特征?
1. 定义: 两组对边分别平行的四边形叫做平行四边形.
2.记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,
相对的角称为对角.
概念
活动 将两个全等的三角形纸片相等的边重合在一起,你能拼出平行四边形吗?你能拼出几个?与同学交流你的拼法,并把它展示出来.
说一说:通过拼图你可以得到什么结论?
平行四边形对边相等,对角相等,邻角互补.
一
这个结论正确吗?
(三)动手操作、探究新知
A
B
C
D
平行四边形问题
转化
三角形问题
证一证
证明:如图,连接AC,
∵AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA.
∴AB=CD,AD=BC,
∠B=∠D.
已知: ABCD,AB∥CD,AD∥BC.
求证: AB=CD,BC=DA;
∠B=∠D, ∠BAD=∠DCB
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3.
即∠BAD=∠DCB.
证明结论
平行四边形的性质
A
B
C
D
∵四边形ABCD是平行四边形 ∴AB=CD, AD=BC.
∠A=∠C,∠B=∠D.
∠A+∠B=180,∠A+∠D=180
性质1 平行四边形的对边相等.
性质2 平行四边形的对角相等、邻角互补.
得出结论
设计意图:培养学生的几何语言表达能力和逻辑推理能力。
1 .如图,在 ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______.
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
(四)尝试应用
典例精析
例1 已知:如图, ABCD中,BE平分∠ABC交于AD于点E.
(1) 如果AE=2,求CD的长;
(2)如果∠AEB=40?,求∠C的度数.
B
A
D
C
E
2. 已知: ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
B
A
D
C
E
F
A
D
B
C
E
F
1.已知:如图, ABCD中,BE平分∠ABC交于AD于点E,交CD的延长线于点F.
(1) 如果AE=2,BC=3,求DF的长;
(2)找出图中的等腰三角形.
00:12:29
本节课的交流学习你有哪
些收获呢?与大家分享一下
吧!
【学生活动】
我的收获是……
我感到最困惑的是……
今后我的学习打算是……
(五)反思小结
(六) 作业设计
1、必做题:教材78页练习1、2、3 题
2、选做题:学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
设计意图:针对学生个体差异进行分层训练,既使学生掌握基础知识,又达到“拔尖”和“减负”的目的;进一步弥补课堂中教与学的不足。
A1
A3
A2
A
B
C
平行四边形的性质
板书设计
性质2 平行四边形对角相等
2.性质
性质1 平行四边形对边相等
1.定义:
A
D
B
C
ABCD
记作:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
∴AB=CD AD=BC
∠A=∠C ∠B=∠D
∵四边形ABCD是平行四边形
几何语言
3.例题讲解:
教学反思
本节课根据学生的认知规律,本着激发兴趣,提高抽象概括和逻辑推理能力的原则设计的。由易到难,突破难点,突出重点,充分发挥学生的主体地位,使学生在自主探索,积极思考,合作交流的过程中掌握基础知识和基本技能,体会转化的数学思想,积累数学活动经验。
