2020-2021学年八年级数学人教版下册 18.2.1 《矩形》同步基础练习卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册 18.2.1 《矩形》同步基础练习卷(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 352.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 13:44:45 | ||
图片预览


文档简介
2021年人教版八年级数学下册
《矩形》同步基础练习卷
一、选择题
1.下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分
D.矩形的对角线相等且互相平分
2.在□ABCD中,AC交BD于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的条件是( )
A.AB=AD B.OA=OB C.AC=BD D.DC⊥BC
3.如图,四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:
①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.
则不能使四边形ABCD成为矩形的是( )
A.①②③ B.②③④ C.②⑤⑥ D.④⑤⑥
4.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠1=∠2
5.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.AB=DC
6.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否为直角
D.测量四边形的其中三个角是否都为直角
7.有下列说法:
①四个角都相等的四边形是矩形;
②有一组对边平行,有两个角为直角的四边形是矩形;
③两组对边分别相等且有一个角为直角的四边形是矩形;
④对角线相等且有一个角是直角的四边形是矩形;
⑤对角线互相平分且相等的四边形是矩形;
⑥一组对边平行,另一组对边相等且有一角为直角的四边形是矩形.
其中,正确的个数是( )
A.2个 B.3个 C.4个 D.5个
8.检查一个门框是否为矩形,下列方法中正确的是( )
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.测量门框的三个角,是否都是直角
D.测量两条对角线,是否互相垂直
9.如图,将矩形纸片ABCD沿对角线BD折叠一次,则图中全等三角形有(??? )
A.2对?? ?? B. 3对?? C. 4对??? D.5对
10.如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为( )
A.1 B.2 C.3 D.4
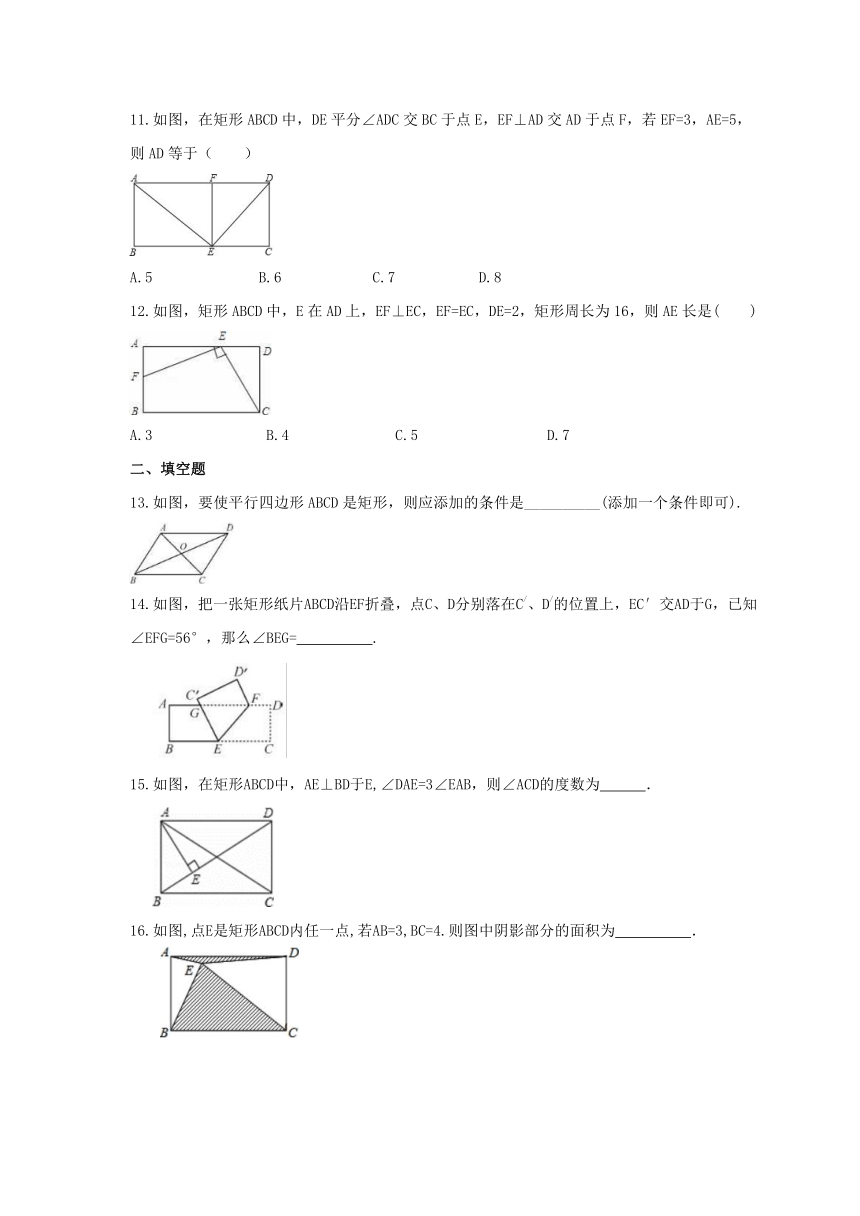
11.如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( )
A.5 B.6 C.7 D.8
12.如图,矩形ABCD中,E在AD上,EF⊥EC,EF=EC,DE=2,矩形周长为16,则AE长是( )
A.3??? B.4?? ? C.5??? D.7
二 、填空题
13.如图,要使平行四边形ABCD是矩形,则应添加的条件是__________(添加一个条件即可).
14.如图,把一张矩形纸片ABCD沿EF折叠,点C、D分别落在C/、D/的位置上,EC′交AD于G,已知∠EFG=56°,那么∠BEG= .
15.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠ACD的度数为 .
16.如图,点E是矩形ABCD内任一点,若AB=3,BC=4.则图中阴影部分的面积为 .
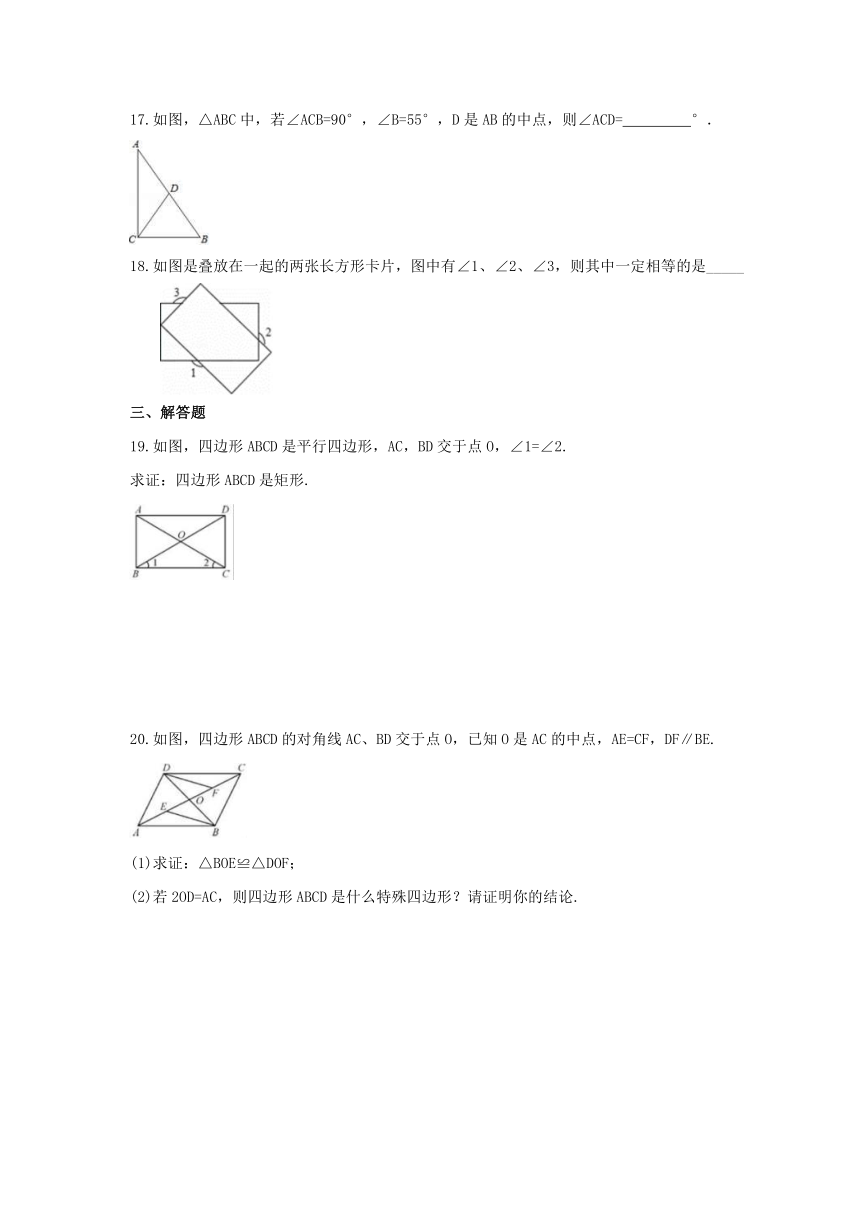
17.如图,△ABC中,若∠ACB=90°,∠B=55°,D是AB的中点,则∠ACD= ?? °.
18.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____
三 、解答题
19.如图,四边形ABCD是平行四边形,AC,BD交于点O,∠1=∠2.
求证:四边形ABCD是矩形.
20.如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若2OD=AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
21.如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE.
(2)连结DE,线段DE与AB之间有怎样的位置关系和数量关系?请证明你的结论.
22.如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F。
(1)求证:AC=BE;
(2)若∠AFC=2∠D,连接AC,BE.求证:四边形ABEC是矩形。
23.如图,已知在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.
求证:AE平分∠BAD.
24.如图,在?ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.
25.如图,在矩形ABCD中,AB=6,BC=8.将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求四边形ABCE的面积.
参考答案
1.D
2.A
3.C
4.C
5.C
6.D
7.C
8.C
9.C
10.B.
11.C
12.A
13.答案为:不唯一,如:∠ABC=90°或AC=BD
14.答案为:68°
15.答案为:67.5°,
16.答案为:6;
17.答案为:35?
18.答案为:∠2=∠3
19.证明:∵∠1=∠2,
∴BO=CO,即2BO=2CO.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=OD.
∴AC=2CO,BD=2BO.
∴AC=BD.
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
20.证明:(1)∵O是AC的中点,∴OA=OC.
∵AE=CF,∴OE=OF.
∵DF∥BE,∴∠OEB=∠OFD.
又∵∠EOB=∠FOD,
∴△BOE≌△DOF.
(2)∵△BOE≌△DOF,∴OD=OB.
∵OA=OC,
∴四边形ABCD是平行四边形.
∵OD=0.5AC,OD=0.5BD,
∴AC=BD,
∴四边形ABCD是矩形.
21. (1)证明:因为AB=AC,
所以∠B=∠ACB,
又因为AD是BC边上的中线,
所以AD⊥BC,即∠ADB=90°.
因为AE∥BC,所以∠EAC=∠ACB,
所以∠B=∠EAC.
因为CE⊥AE,所以∠CEA=90°,
所以∠ADB=∠CEA.
又AB=CA,
所以△ABD≌△CAE(A.A.S.).
(2)解:AB∥DE且AB=DE.
证明:由△ABD≌△CAE可得AE=BD,
又AE∥BD,所以四边形ABDE是平行四边形,所以AB∥DE且AB=DE.
22.证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∵CE=DC,∴AB=EC,AB∥EC,∴四边形ABEC是平行四边形,
∴AC=BE;
(2)∵AB=EC,AB∥EC,∴四边形ABEC是平行四边形,
∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,∴∠ABC=∠D,
又∵∠AFC=2∠D,∴∠AFC=2∠ABC,
∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB,
∴FA=FE=FB=FC,∴AE=BC,∴四边形ABEC是矩形。
23.提示:证明△BFE≌△CED,
从而BE=DC=AB,
∴∠BAE=45°,
可得AE平分∠BAD
24.证明:∵F为BE中点,AF=BF,
∴AF=BF=EF,
∴∠BAF=∠ABF,∠FAE=∠AEF,
在△ABE中,∠BAF+∠ABF+∠FAE+∠AEF=180°,
∴∠BAF+∠FAE=90°,
又四边形ABCD为平行四边形,
∴四边形ABCD为矩形;
(2)解:连接EG,过点E作EH⊥BC,垂足为H,
∵F为BE的中点,FG⊥BE,
∴BG=GE,
∵S△BFG=5,CD=4,
∴S△BGE=10=0.5BG?EH,
∴BG=GE=5,
在Rt△EGH中,GH=3,
在Rt△BEH中,BE=4=BC,
∴CG=BC﹣BG=4﹣5
25.解:(1)设EF=x依题意知:△CDE≌△CFE,
∴DE=EF=x,CF=CD=6.
∵在Rt△ACD中,AC==10,
∴AF=AC﹣CF=4,AE=AD﹣DE=8﹣x.
在Rt△AEF中,有AE2=AF2+EF2
即(8﹣x)2=42+x2
解得x=3,即:EF=3.
(2)由(1)知:AE=8﹣3=5,
∴S梯形ABCE==(5+8)×6÷2=39.
《矩形》同步基础练习卷
一、选择题
1.下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分
D.矩形的对角线相等且互相平分
2.在□ABCD中,AC交BD于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的条件是( )
A.AB=AD B.OA=OB C.AC=BD D.DC⊥BC
3.如图,四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:
①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.
则不能使四边形ABCD成为矩形的是( )
A.①②③ B.②③④ C.②⑤⑥ D.④⑤⑥
4.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠1=∠2
5.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.AB=DC
6.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否为直角
D.测量四边形的其中三个角是否都为直角
7.有下列说法:
①四个角都相等的四边形是矩形;
②有一组对边平行,有两个角为直角的四边形是矩形;
③两组对边分别相等且有一个角为直角的四边形是矩形;
④对角线相等且有一个角是直角的四边形是矩形;
⑤对角线互相平分且相等的四边形是矩形;
⑥一组对边平行,另一组对边相等且有一角为直角的四边形是矩形.
其中,正确的个数是( )
A.2个 B.3个 C.4个 D.5个
8.检查一个门框是否为矩形,下列方法中正确的是( )
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.测量门框的三个角,是否都是直角
D.测量两条对角线,是否互相垂直
9.如图,将矩形纸片ABCD沿对角线BD折叠一次,则图中全等三角形有(??? )
A.2对?? ?? B. 3对?? C. 4对??? D.5对
10.如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为( )
A.1 B.2 C.3 D.4
11.如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( )
A.5 B.6 C.7 D.8
12.如图,矩形ABCD中,E在AD上,EF⊥EC,EF=EC,DE=2,矩形周长为16,则AE长是( )
A.3??? B.4?? ? C.5??? D.7
二 、填空题
13.如图,要使平行四边形ABCD是矩形,则应添加的条件是__________(添加一个条件即可).
14.如图,把一张矩形纸片ABCD沿EF折叠,点C、D分别落在C/、D/的位置上,EC′交AD于G,已知∠EFG=56°,那么∠BEG= .
15.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠ACD的度数为 .
16.如图,点E是矩形ABCD内任一点,若AB=3,BC=4.则图中阴影部分的面积为 .
17.如图,△ABC中,若∠ACB=90°,∠B=55°,D是AB的中点,则∠ACD= ?? °.
18.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____
三 、解答题
19.如图,四边形ABCD是平行四边形,AC,BD交于点O,∠1=∠2.
求证:四边形ABCD是矩形.
20.如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若2OD=AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
21.如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE.
(2)连结DE,线段DE与AB之间有怎样的位置关系和数量关系?请证明你的结论.
22.如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F。
(1)求证:AC=BE;
(2)若∠AFC=2∠D,连接AC,BE.求证:四边形ABEC是矩形。
23.如图,已知在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.
求证:AE平分∠BAD.
24.如图,在?ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.
25.如图,在矩形ABCD中,AB=6,BC=8.将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求四边形ABCE的面积.
参考答案
1.D
2.A
3.C
4.C
5.C
6.D
7.C
8.C
9.C
10.B.
11.C
12.A
13.答案为:不唯一,如:∠ABC=90°或AC=BD
14.答案为:68°
15.答案为:67.5°,
16.答案为:6;
17.答案为:35?
18.答案为:∠2=∠3
19.证明:∵∠1=∠2,
∴BO=CO,即2BO=2CO.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=OD.
∴AC=2CO,BD=2BO.
∴AC=BD.
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
20.证明:(1)∵O是AC的中点,∴OA=OC.
∵AE=CF,∴OE=OF.
∵DF∥BE,∴∠OEB=∠OFD.
又∵∠EOB=∠FOD,
∴△BOE≌△DOF.
(2)∵△BOE≌△DOF,∴OD=OB.
∵OA=OC,
∴四边形ABCD是平行四边形.
∵OD=0.5AC,OD=0.5BD,
∴AC=BD,
∴四边形ABCD是矩形.
21. (1)证明:因为AB=AC,
所以∠B=∠ACB,
又因为AD是BC边上的中线,
所以AD⊥BC,即∠ADB=90°.
因为AE∥BC,所以∠EAC=∠ACB,
所以∠B=∠EAC.
因为CE⊥AE,所以∠CEA=90°,
所以∠ADB=∠CEA.
又AB=CA,
所以△ABD≌△CAE(A.A.S.).
(2)解:AB∥DE且AB=DE.
证明:由△ABD≌△CAE可得AE=BD,
又AE∥BD,所以四边形ABDE是平行四边形,所以AB∥DE且AB=DE.
22.证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∵CE=DC,∴AB=EC,AB∥EC,∴四边形ABEC是平行四边形,
∴AC=BE;
(2)∵AB=EC,AB∥EC,∴四边形ABEC是平行四边形,
∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,∴∠ABC=∠D,
又∵∠AFC=2∠D,∴∠AFC=2∠ABC,
∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB,
∴FA=FE=FB=FC,∴AE=BC,∴四边形ABEC是矩形。
23.提示:证明△BFE≌△CED,
从而BE=DC=AB,
∴∠BAE=45°,
可得AE平分∠BAD
24.证明:∵F为BE中点,AF=BF,
∴AF=BF=EF,
∴∠BAF=∠ABF,∠FAE=∠AEF,
在△ABE中,∠BAF+∠ABF+∠FAE+∠AEF=180°,
∴∠BAF+∠FAE=90°,
又四边形ABCD为平行四边形,
∴四边形ABCD为矩形;
(2)解:连接EG,过点E作EH⊥BC,垂足为H,
∵F为BE的中点,FG⊥BE,
∴BG=GE,
∵S△BFG=5,CD=4,
∴S△BGE=10=0.5BG?EH,
∴BG=GE=5,
在Rt△EGH中,GH=3,
在Rt△BEH中,BE=4=BC,
∴CG=BC﹣BG=4﹣5
25.解:(1)设EF=x依题意知:△CDE≌△CFE,
∴DE=EF=x,CF=CD=6.
∵在Rt△ACD中,AC==10,
∴AF=AC﹣CF=4,AE=AD﹣DE=8﹣x.
在Rt△AEF中,有AE2=AF2+EF2
即(8﹣x)2=42+x2
解得x=3,即:EF=3.
(2)由(1)知:AE=8﹣3=5,
∴S梯形ABCE==(5+8)×6÷2=39.
