2020-2021学年人教版八年级数学下册19.1.2 函数的图象(28张PPT)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册19.1.2 函数的图象(28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 23:42:02 | ||
图片预览






文档简介
(共28张PPT)
19.1.2
函数的图象(2)
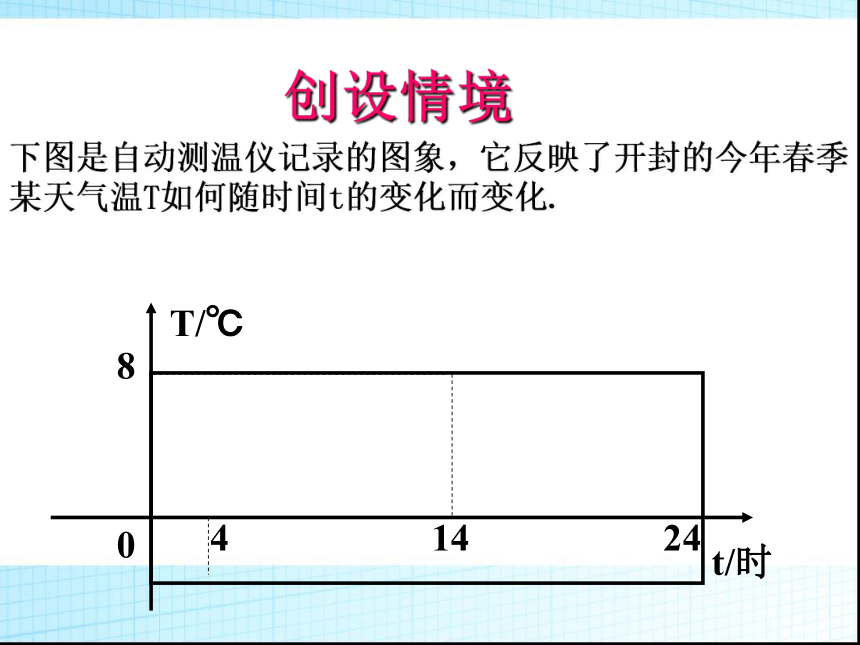
创设情境
下图是自动测温仪记录的图象,它反映了开封的今年春季
某天气温T如何随时间t的变化而变化.
4
14
24
t/时
8
T/℃
0
学习目标
1.会观察函数图象;
2.能结合函数图像对简单实际问题中的函数关系和变化趋势进行分析,从中获取信息,解决问题;
3.了解数形结合思想,体会数学来源于生活又应用于生活.
复习提问
一般地,在一个变化过程
中,如果有两个变量
x
与y,并且对于
x
的每一个确定的值,
y
都有唯一确定的值与其对应,那么我们就说
x
是自变量,y
是
x
的函数.
1.函数的定义:
22一般地,对于一个函数,如果把自变量与函数的每对对应的值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
2.函数的图像:
函数——
自变量x
,函数值y
点——
(横坐标
,
纵坐标)
探究新知
下图是自动测温仪记录的图象,它反映了开封的今年春季某天气温T如何随时间t的变化而变化.
4
14
24
t/时
8
T/℃
0
4
14
24
t/时
8
T/℃
0
?
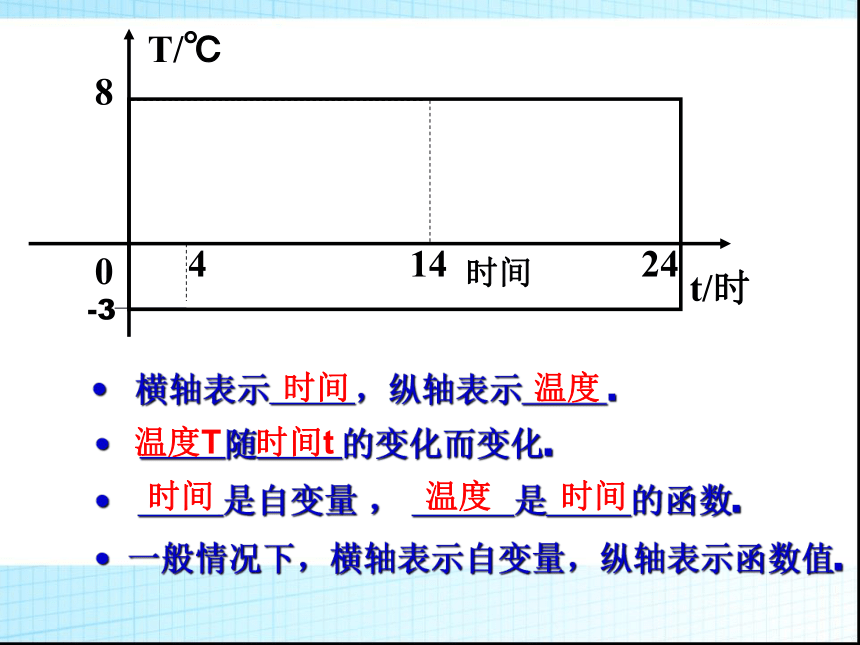
横轴表示_____,纵轴表示_____.
?
_____随_____的变化而变化.
-3
时间
温度
时间
温度T
时间t
?
_____是自变量
,
______是_____的函数.
时间
温度
时间
?
一般情况下,横轴表示自变量,纵轴表示函数值.
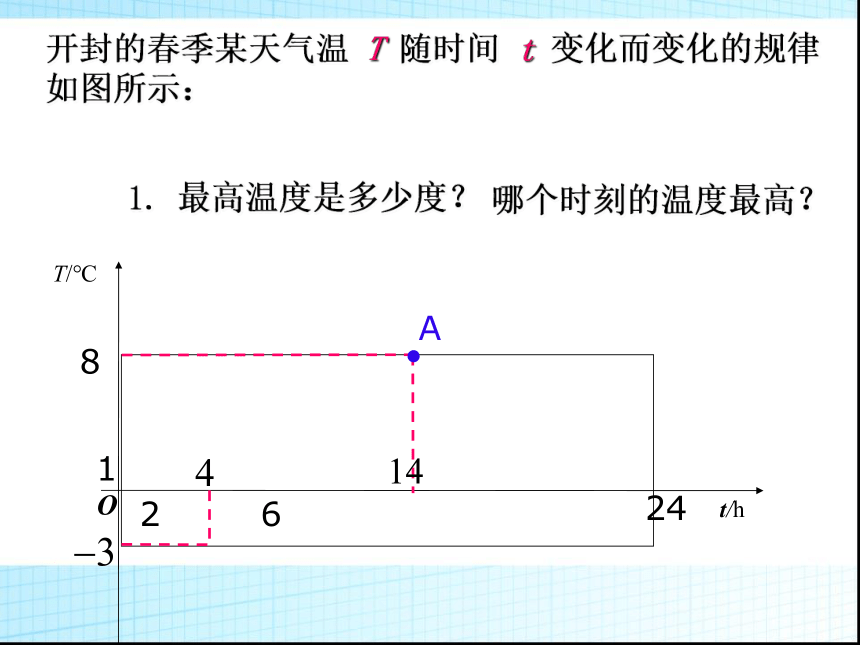
开封的春季某天气温
T
随时间
t
变化而变化的规律如图所示:
1.
最高温度是多少度?
哪个时刻的温度最高?
24
6
O
t/h
2
T/℃
1
8
A
?
24
6
O
t/h
2
T/℃
1
8
2.
最低温度是多少度?
哪个时刻的温度最低?
?
B
24
6
O
t/h
2
T/℃
1
8
3.图像上的哪一段时间表示温度在上升?
图像上的哪一段时间表示温度在下降?
24
6
O
t/h
2
T/℃
1
8
4.图像与x轴的交点表示什么意义?
与y轴的交点呢?
?
C
?
D
?
E
总结
看图像的方法
1.
了解横、纵轴的意义
2.
从函数图象上判定函数与自变量的关系
3.
抓住特殊点的实际意义
一看坐标轴
二看特殊点
三看变化趋势
下图反映的过程是小明从家去食堂吃早餐,
接着去图书馆读报,然后回家.其中x
表示时间,y
表
示小明离家的距离,小明家、食堂、图书馆在同一直线
上.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
从家到食堂
从食堂到图书馆
从图书馆回家
学以致用
解(1)由纵坐标看
出,菜地离小明
家1.1千米;由横
坐标看出小明走
到菜地用了15分
种。
解:由纵坐标看出,食堂离小明家0.6千米,由横坐标看出,小明从家到食堂用了8分钟.
根据图象回答下列问题:
1.
食堂离小明家多远?
小明从家到食堂用了多长时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
2.小明吃早餐用了多少时间?
(2)由横坐标看
出,小明给菜地浇
水用了10分。
(25-10)
解:由横坐标看出,25-8=17,小明吃早餐用了17分钟.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
3.食堂离图书馆多远?
小明从食堂到图书馆用了多少时间?
解:由纵坐标看出,0.8-0.6=0.2,食堂离图书馆0.2千米;由横坐标看出,28-25=3,小明从食堂到图书馆用了3分钟.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
4.小明读报用了多少时间?
解:由横坐标看出,58-28=30,小明读报用了30分钟.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
5.图书馆离小明家多远?
小明从图书馆回家的平均速度是多少?
解:由纵坐标看出,图书馆离小明0.8千米;
由横坐标看出,68-58=10;小明从图书馆回家用了10分钟,由此算出平均速度为0.08千米/分.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
?
当函数图象从左向右上升时,函数值y随自变量x的增大而
总结
图像变化规律
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
?
当函数图象从左向右下降
时,函数值y随自变量x的增大而
?
当函数图象某段平行于x轴时,则此段上的函数值y
增大,
减小.
不变.
函数图像上升时,y随x的增大而增大;
函数图像下降时,y随x的增大而减小.
课堂小练兵
1.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是(
)
C
2.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是(
)
D
3.周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离开家后的距离S(千米)与时间t(时)的关系可以用图中的曲线表示.根据这个图象回答下列问题:
(1)小李到达离家最远的地方是什么时间?
(2)小李何时第一次休息?
(3)10时到13时,小骑了多少千米?
(4)返回时,小李的平均车速是多少?
4、(中招题)甲,乙两同学骑自行车从A地沿同一条路到B地,
已知乙比甲先出发.他们离出发地的距离s/km和骑行时间
t/h之间的函数关系如图所示,给出下列说法:
a.他们都骑了20km;
b.乙在途中停留了0.5h;
c.甲和乙两人同时到达目的地;
d.相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的是 ( )
B
t/h
A.1个
B.2个
D.4个
C.3个
甲
乙
s/km
请谈谈你的收获
(1)你认为观察函数图象时要注意哪些问题?
图象信息(形)
图象上点的坐标(数)
对应关系和变化规律
(数形结合)
课堂小结
(2)对你的生活有哪些帮助?
A层
习题19.1第9、13题.
B层
习题19.1第9题
C层
习题19.1第8题
今日作业
感谢同学们的陪伴!
19.1.2
函数的图象(2)
创设情境
下图是自动测温仪记录的图象,它反映了开封的今年春季
某天气温T如何随时间t的变化而变化.
4
14
24
t/时
8
T/℃
0
学习目标
1.会观察函数图象;
2.能结合函数图像对简单实际问题中的函数关系和变化趋势进行分析,从中获取信息,解决问题;
3.了解数形结合思想,体会数学来源于生活又应用于生活.
复习提问
一般地,在一个变化过程
中,如果有两个变量
x
与y,并且对于
x
的每一个确定的值,
y
都有唯一确定的值与其对应,那么我们就说
x
是自变量,y
是
x
的函数.
1.函数的定义:
22一般地,对于一个函数,如果把自变量与函数的每对对应的值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
2.函数的图像:
函数——
自变量x
,函数值y
点——
(横坐标
,
纵坐标)
探究新知
下图是自动测温仪记录的图象,它反映了开封的今年春季某天气温T如何随时间t的变化而变化.
4
14
24
t/时
8
T/℃
0
4
14
24
t/时
8
T/℃
0
?
横轴表示_____,纵轴表示_____.
?
_____随_____的变化而变化.
-3
时间
温度
时间
温度T
时间t
?
_____是自变量
,
______是_____的函数.
时间
温度
时间
?
一般情况下,横轴表示自变量,纵轴表示函数值.
开封的春季某天气温
T
随时间
t
变化而变化的规律如图所示:
1.
最高温度是多少度?
哪个时刻的温度最高?
24
6
O
t/h
2
T/℃
1
8
A
?
24
6
O
t/h
2
T/℃
1
8
2.
最低温度是多少度?
哪个时刻的温度最低?
?
B
24
6
O
t/h
2
T/℃
1
8
3.图像上的哪一段时间表示温度在上升?
图像上的哪一段时间表示温度在下降?
24
6
O
t/h
2
T/℃
1
8
4.图像与x轴的交点表示什么意义?
与y轴的交点呢?
?
C
?
D
?
E
总结
看图像的方法
1.
了解横、纵轴的意义
2.
从函数图象上判定函数与自变量的关系
3.
抓住特殊点的实际意义
一看坐标轴
二看特殊点
三看变化趋势
下图反映的过程是小明从家去食堂吃早餐,
接着去图书馆读报,然后回家.其中x
表示时间,y
表
示小明离家的距离,小明家、食堂、图书馆在同一直线
上.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
从家到食堂
从食堂到图书馆
从图书馆回家
学以致用
解(1)由纵坐标看
出,菜地离小明
家1.1千米;由横
坐标看出小明走
到菜地用了15分
种。
解:由纵坐标看出,食堂离小明家0.6千米,由横坐标看出,小明从家到食堂用了8分钟.
根据图象回答下列问题:
1.
食堂离小明家多远?
小明从家到食堂用了多长时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
2.小明吃早餐用了多少时间?
(2)由横坐标看
出,小明给菜地浇
水用了10分。
(25-10)
解:由横坐标看出,25-8=17,小明吃早餐用了17分钟.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
3.食堂离图书馆多远?
小明从食堂到图书馆用了多少时间?
解:由纵坐标看出,0.8-0.6=0.2,食堂离图书馆0.2千米;由横坐标看出,28-25=3,小明从食堂到图书馆用了3分钟.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
4.小明读报用了多少时间?
解:由横坐标看出,58-28=30,小明读报用了30分钟.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
5.图书馆离小明家多远?
小明从图书馆回家的平均速度是多少?
解:由纵坐标看出,图书馆离小明0.8千米;
由横坐标看出,68-58=10;小明从图书馆回家用了10分钟,由此算出平均速度为0.08千米/分.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
?
当函数图象从左向右上升时,函数值y随自变量x的增大而
总结
图像变化规律
8
25
28
58
68
x/min
0.8
0.6
y/km
O
A
B
E
D
C
?
当函数图象从左向右下降
时,函数值y随自变量x的增大而
?
当函数图象某段平行于x轴时,则此段上的函数值y
增大,
减小.
不变.
函数图像上升时,y随x的增大而增大;
函数图像下降时,y随x的增大而减小.
课堂小练兵
1.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是(
)
C
2.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是(
)
D
3.周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离开家后的距离S(千米)与时间t(时)的关系可以用图中的曲线表示.根据这个图象回答下列问题:
(1)小李到达离家最远的地方是什么时间?
(2)小李何时第一次休息?
(3)10时到13时,小骑了多少千米?
(4)返回时,小李的平均车速是多少?
4、(中招题)甲,乙两同学骑自行车从A地沿同一条路到B地,
已知乙比甲先出发.他们离出发地的距离s/km和骑行时间
t/h之间的函数关系如图所示,给出下列说法:
a.他们都骑了20km;
b.乙在途中停留了0.5h;
c.甲和乙两人同时到达目的地;
d.相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的是 ( )
B
t/h
A.1个
B.2个
D.4个
C.3个
甲
乙
s/km
请谈谈你的收获
(1)你认为观察函数图象时要注意哪些问题?
图象信息(形)
图象上点的坐标(数)
对应关系和变化规律
(数形结合)
课堂小结
(2)对你的生活有哪些帮助?
A层
习题19.1第9、13题.
B层
习题19.1第9题
C层
习题19.1第8题
今日作业
感谢同学们的陪伴!
