2020-2021学年北师大版七年级数学下册第五章生活中的轴对称单元综合提升训练(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第五章生活中的轴对称单元综合提升训练(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 315.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 17:03:29 | ||
图片预览

文档简介
2021年度北师大版七年级数学下册《第5章生活中的轴对称》单元同步提升训练(附答案)
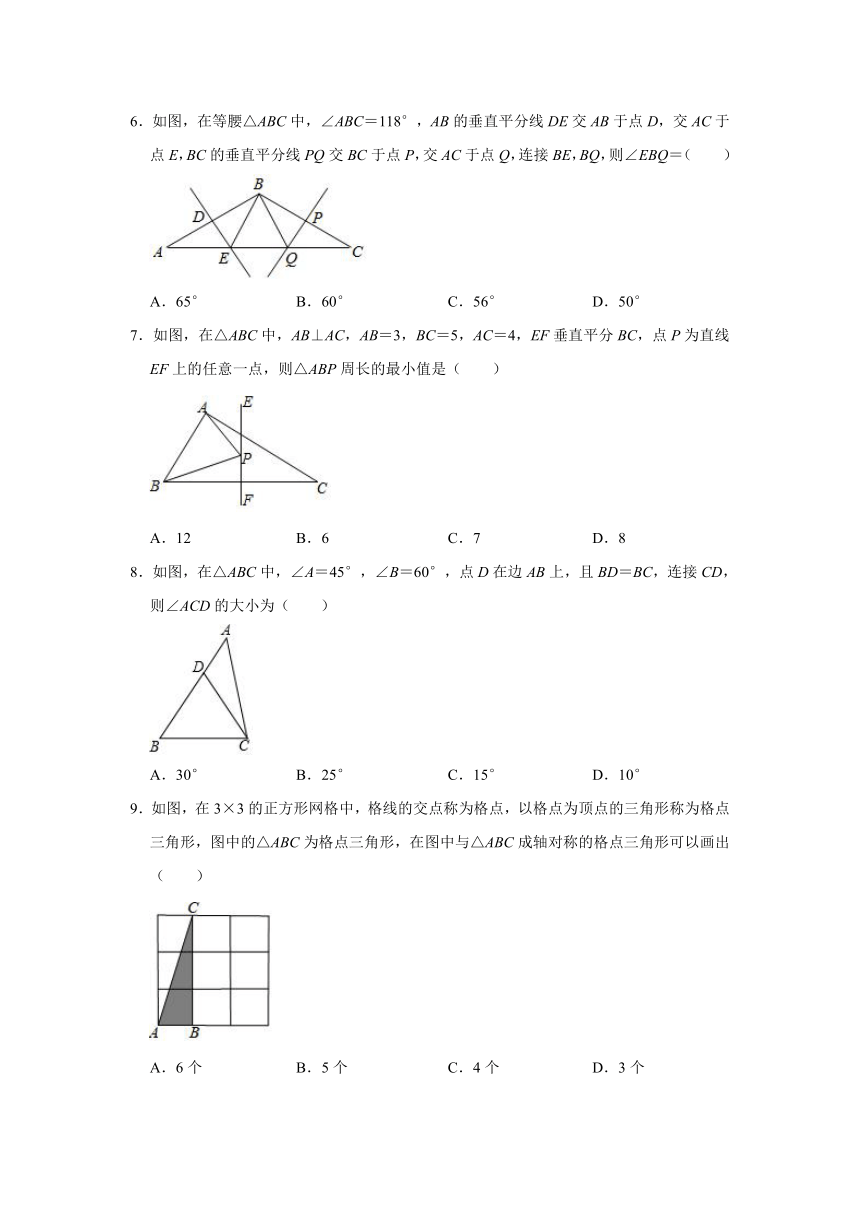
1.下列图案不是轴对称图形的是( )
A. B. C. D.
2.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是( )
A.AD⊥BC B.EF=FD C.BE=BD D.AE=AC
3.如图,在△ABC中,∠A=87°,∠ABC的平分线BD交AC于点D,E是BC中点,且DE⊥BC,那么∠C的度数为( )
A.16° B.28° C.31° D.62°
4.下列四个说法:
①等腰三角形的腰一定大于其腰上的高;②等腰三角形的两腰上的中线长相等;
③等腰三角形的高、中线、角平分线互相重合;
④等腰三角形的一边为5,另一边为10,则它的周长为20或25.
其中正确的个数为( )
A.1个 B.2 C.3 D.4
5.如图,在△ABC中,AC的垂直平分线交边AC于点D,交边BC于点E,连接AE.若AB=6,BC=9,则△ABE的周长为( )
A.24 B.21 C.18 D.15
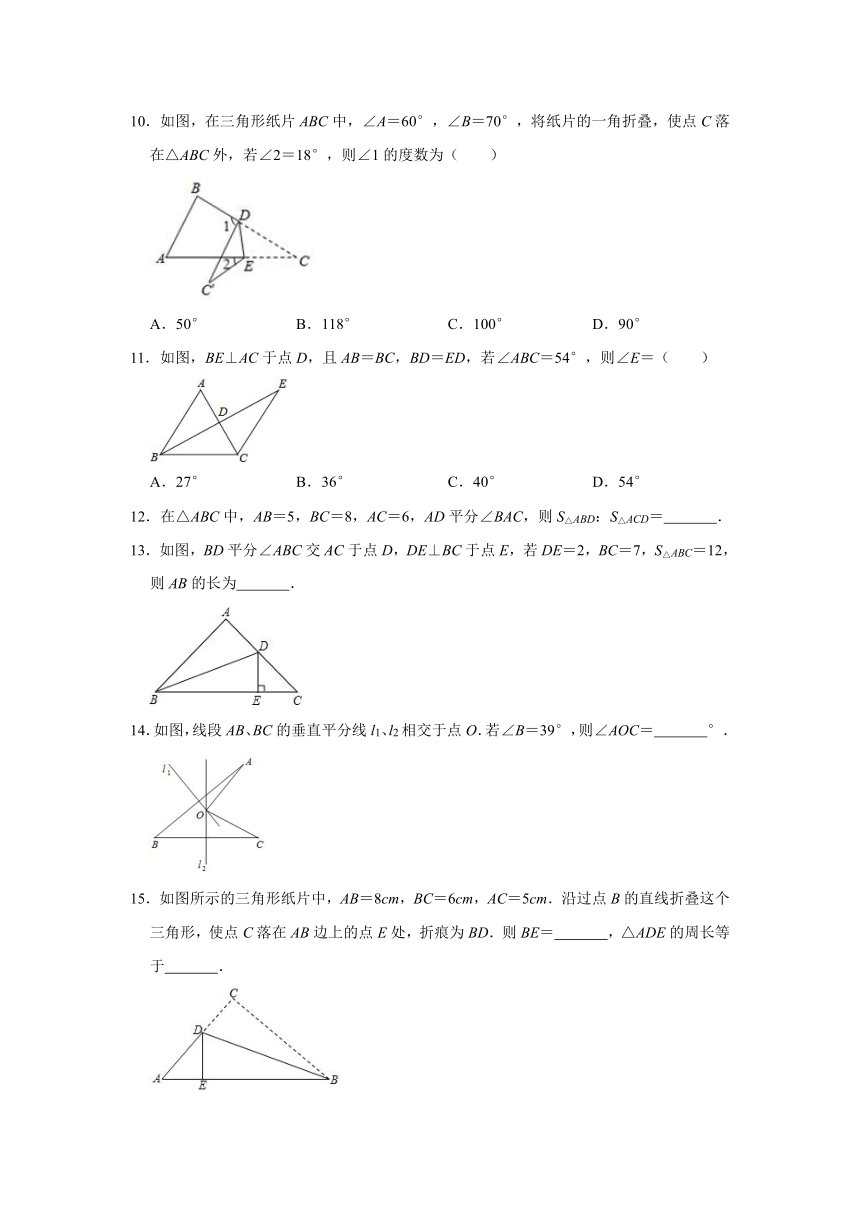
6.如图,在等腰△ABC中,∠ABC=118°,AB的垂直平分线DE交AB于点D,交AC于点E,BC的垂直平分线PQ交BC于点P,交AC于点Q,连接BE,BQ,则∠EBQ=( )
A.65° B.60° C.56° D.50°
7.如图,在△ABC中,AB⊥AC,AB=3,BC=5,AC=4,EF垂直平分BC,点P为直线EF上的任意一点,则△ABP周长的最小值是( )
A.12 B.6 C.7 D.8
8.如图,在△ABC中,∠A=45°,∠B=60°,点D在边AB上,且BD=BC,连接CD,则∠ACD的大小为( )
A.30° B.25° C.15° D.10°
9.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形可以画出( )
A.6个 B.5个 C.4个 D.3个
10.如图,在三角形纸片ABC中,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为( )
A.50° B.118° C.100° D.90°
11.如图,BE⊥AC于点D,且AB=BC,BD=ED,若∠ABC=54°,则∠E=( )
A.27° B.36° C.40° D.54°
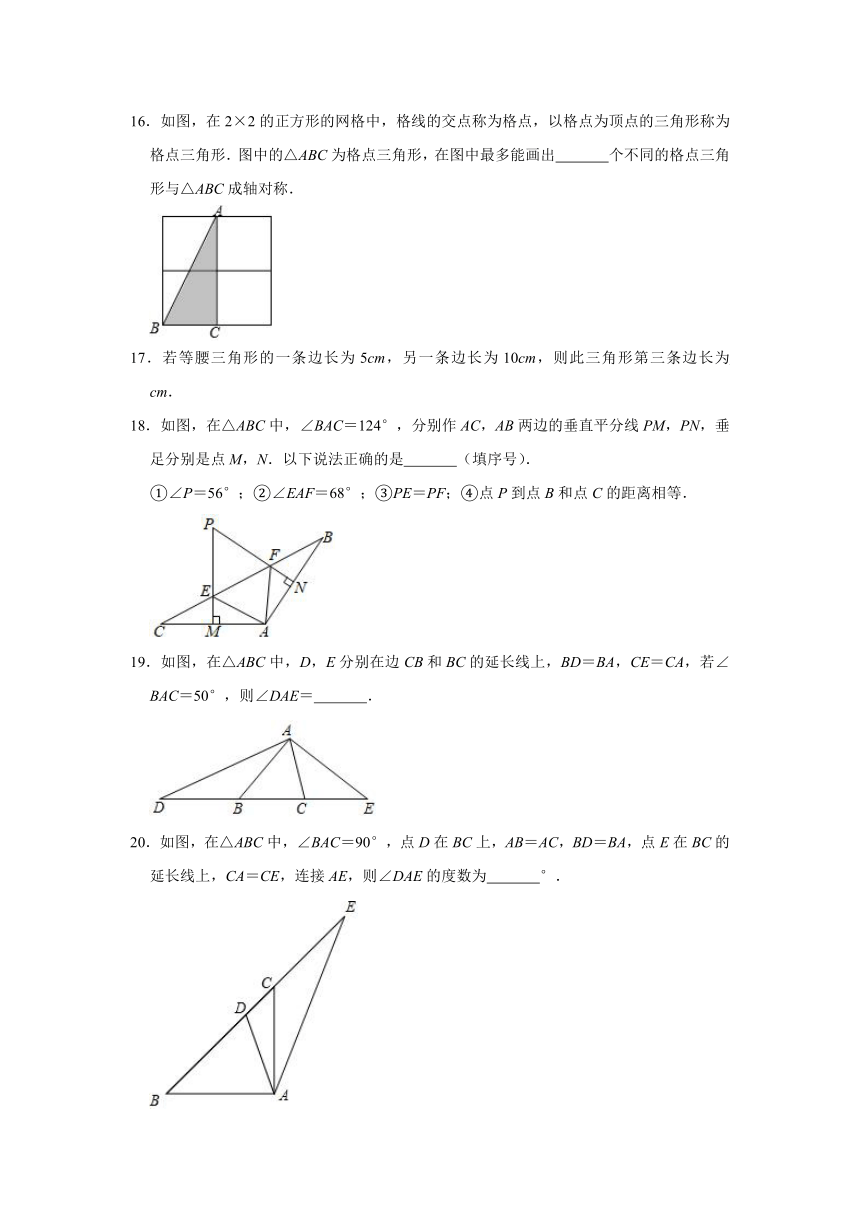
12.在△ABC中,AB=5,BC=8,AC=6,AD平分∠BAC,则S△ABD:S△ACD= .
13.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若DE=2,BC=7,S△ABC=12,则AB的长为 .
14.如图,线段AB、BC的垂直平分线l1、l2相交于点O.若∠B=39°,则∠AOC= °.
15.如图所示的三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD.则BE= ,△ADE的周长等于 .
16.如图,在2×2的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC为格点三角形,在图中最多能画出 个不同的格点三角形与△ABC成轴对称.
17.若等腰三角形的一条边长为5cm,另一条边长为10cm,则此三角形第三条边长为 cm.
18.如图,在△ABC中,∠BAC=124°,分别作AC,AB两边的垂直平分线PM,PN,垂足分别是点M,N.以下说法正确的是 (填序号).
①∠P=56°;②∠EAF=68°;③PE=PF;④点P到点B和点C的距离相等.
19.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE= .
20.如图,在△ABC中,∠BAC=90°,点D在BC上,AB=AC,BD=BA,点E在BC的延长线上,CA=CE,连接AE,则∠DAE的度数为 °.
21.如图,在△ABC中,AB的垂直平分线DE分别与AB、BC交于点D、E,AC的垂直平分线FG分别与BC、AC交于点F、G,BC=10,EF=3,则△AEF的周长是 .
22.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=86°,则∠CAD的度数是 .
23.如图,在△ABC中,AB<AC<BC,以点A为圆心,线段AB的长为半径画弧,与BC边交于点D,连接AD过点D作DE⊥AD,交AC于点E.
(1)若∠B=50°,∠C=28°,求∠AED度数;
(2)若点F是BD的中点,连接AF,求证:∠BAF=∠EDC.
24.如图,在△ABP中,∠ABP=60°,90°<∠APB<120°,过点A的直线l垂直于线段BP所在的直线.设点B,P关于直线l的对称点分别为点B′,P′
(1)在图中画出△ABP关于直线l对称的三角形△AB′P′.
(2)若∠BAP=α,求∠AP′B的度数.(用α表示)
(3)若点P′关于直线AB′的对称点为M,连接AM,PM.请写出PA、PM之间的数量关系和位置关系,并证明你的结论.
25.问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由.
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
26.在△ABC中,∠ABC和∠ACB的平分线相交于点O,
(1)若∠ABC=60°,∠ACB=40°,求∠BOC的度数;
(2)若∠ABC=60°,OB=4,且△ABC的周长为16,求△ABC的面积.
27.阅读:在同一个三角形中,相等的边所对的角相等,简称为“等边对等角”.
例如,在△ABC中,如果AB=AC,依据“等边对等角”可得∠B=∠C.
请运用上述知识,解决问题:
已知:如图,△ABC中,AD⊥BC于D,BE是三角形的角平分线,交AD于F.
(1)若∠ABC=40°,求∠AFE的度数.
(2)若AE=AF,试判断△ABC的形状,并写出证明过程.
28.已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
29.如图,△ABC中,BA=BC,点D是AC延长线上一点,平面上一点E,连接EB、EC、ED、BD,CB平分∠ACE.
(1)若∠ABC=50°,求∠DCE的度数;
(2)若∠ABC=∠DBE,求证:AD=CE.
参考答案
1.解:A、不是轴对称图形,故此选项符合题意;
B、是轴对称图形,故此选项不合题意;
C、是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项不符合题意;
故选:A.
2.解:∵△ABC是等边三角形,△AED是等边三角形,
∴AB=AC=BC,∠BAC=60°,AE=AD=ED,∠EAD=60°,
∴∠DAB=∠DAC=30°,
∴AD⊥BC,故①正确,∠EAB=∠BAD=30°,
∴AB⊥ED,EF=DF,故②正确
∴BE=BD,故③正确,
无法得出AC=AE,故④错误;故选:D.
3.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE⊥BC,E是BC中点,
∴DB=DC,
∴∠DBC=∠C,
∴∠ABD=∠CBD=∠C,
∴∠ABD+∠CBD+∠C=180°﹣87°,
解得,∠C=31°,故选:C.
4.解:如图1,
在Rt△ABC中,AC=BC=BD,
∴等腰三角形的腰一定大于或等于其腰上的高,故①错误;
如图2,∵AB=AC,AD=DC,AE=EB,
∴DC=BE,∠DCB=∠EBC.
在△BDC和△CEB中,
,
∴△BDC≌△CEB(SAS).
∴BD=CE,故②正确;
∵等腰三角形的顶角的平分线,底边上的高,底边上的中线互相重合,故③错误;
∵等腰三角形的一边长为5,一边长为10,
∴只能三边是10,10,5,
∴它的周长是25,故④错误.
故选:A.
5.解:∵DE是线段AC的垂直平分线,
∴EA=EC,
∴△ABE的周长=AB+BE+EA=AB+BE+EC=AB+BC,
∵AB=6,BC=9,
∴△ABE的周长=AB+BC=6+9=15,
故选:D.
6.解:等腰△ABC中,∠ABC=118°,
∴∠A=∠C=31°,
∵AB的垂直平分线DE交AB于点D,交AC于点E,BC的垂直平分线PQ交BC于点P,交AC于点Q,
∴EA=EB,QB=QC,
∴∠ABE=∠QBC=∠A=∠C=31°,
∴∠EBQ=∠ABC﹣∠ABE﹣∠QBC=118°﹣31°﹣31°=56°,
故选:C.
7.解:∵EF垂直平分BC,
∴B、C关于EF对称,
设AC交EF于D,
∴当P和D重合时,AP+BP的值最小,最小值等于AC的长,
∵AB=3,AC=4,
∴△ABP周长的最小值是AB+AC=3+4=7.
故选:C.
8.解:在△ABC中,∠A=45°,∠B=60°,
∴∠ACB=180°﹣45°﹣60°=75°,
∵BD=BC,
∴∠BCD=(180°﹣60°)÷2=60°,
∴∠ACD=∠ACB﹣∠BCD=75°﹣60°=15°.
故选:C.
9.解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故选:A.
10.解:在△ABC中,∠A=60°,∠B=70°,
∴∠C=180°﹣∠A﹣∠B=50°.
由折叠,可知:∠CDE=∠C′DE,∠CED=∠C′ED,
∴∠CED==99°,
∴∠CDE=180°﹣∠CED﹣∠C=31°,
∴∠1=180°﹣∠CDE﹣∠C′DE=180°﹣2∠CDE=118°.
故选:B.
11.解:∵AB=BC,BE⊥AC,∠ABC=54°,
∴∠CBD=∠ABD=∠ABC=27°,
∵BE⊥AC,BD=ED,
∴AC是BE的垂直平分线,
∴CB=CE,
∴∠E=∠CBD=27°.
故选:A.
12.解:过D作DE⊥AB于E,DF⊥AC于F,
∵AD平分∠BAC,
∴DE=DF,
设DE=DF=R,
∵S△ABD==R,S△ACD==,
∴S△ABD:S△ACD=5:6,
故答案为:5:6.
13.解:
过D作DF⊥BA,交BA的延长线于F,
∵BD平分∠ABC,DE⊥BC,DE=2,
∴DF=DE=2,
∵BC=7,S△ABC=S△ABD+S△BDC=12,
∴+=12,
∴=12,
解得:AB=5,
故答案为:5.
14.解:连接BO并延长至D,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴OA=OB,OC=OB,
∴∠OAB=∠OBA,∠OCB=∠OBC,
∴∠AOD=2∠OBA,∠COD=2∠OBC,
∴∠AOC=2(∠OBA+∠OBC)=2∠ABC=78°,
故答案为:78.
15.解:∵折叠这个三角形点C落在AB边上的点E处,折痕为BD,
∴BE=BC=6cm,DE=CD,
∴AE=AB﹣BE=AB﹣BC=8﹣6=2(cm),
∴△ADE的周长=AD+DE+AE,=AD+CD+AE,=AC+AE,=5+2,=7(cm).
故答案为:6cm;7cm.
16.解:与△ABC成轴对称的格点三角形如图所示,
在图中最多能画出5个不同的格点三角形与△ABC成轴对称.
故答案为:5.
17.解:当5cm为底时,其它两边都为10cm,
则5cm、10cm、10cm可以构成三角形;
当5cm为腰时,其它两边为5cm和10cm,因为5+5=10,所以不能构成三角形,故舍去.
所以三角形三边长只能是5cm、10cm、10cm,所以第三边是10cm.
故答案为:10.
18.解:∵PM垂直平分AC,PN垂直平分AB,
∴∠PMA=∠PNA=90°,
∴∠P=360°﹣90°﹣90°﹣124°=56°,①说法正确;
∵∠BAC=124°,
∴∠B+∠C=180°﹣124°=56°,
∵PM垂直平分AC,PN垂直平分AB,
∴EC=EA,FB=FA,
∴∠EAC=∠C,∠FAB=∠B,
∴∠EAF=∠BAC﹣∠EAC﹣∠FAB=∠BAC﹣(∠B+∠C)=124°﹣56°=68°,②说法正确;
△ABC不一定是等腰三角形,
∴PE与PF的大小无法确定,③说法错误;
连接PC、PA、PB,
∵PM垂直平分AC,PN垂直平分AB,
∴PC=PA,PB=PA,
∴PB=PC,即点P到点B和点C的距离相等,④说法正确,
故答案为:①②④.
19.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
20.解:∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=(180°﹣∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E=∠ACB=22.5°,
在△ABE中,∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=112.5°﹣67.5°=45°,
故答案为:45.
21.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
同理,FA=FC,
∴△AEF的周长=FA+EF+EA=EB+EF+FC=BC+EF+EF=16,
故答案为:16.
22.解:∵C、D两点在线段AB的中垂线上,
∴CA=CB,DA=DB,
∵CD⊥AB,
∴∠ACD=∠ACB=×50°=25°,∠ADC=∠ADB=×86°=43°,
当点C与点D在线段AB两侧时,∠CAD=180°﹣∠ACD﹣∠ADC=180°﹣25°﹣43°=112°,
当点C与点D′在线段AB同侧时,∠CAD′=∠AD′C﹣∠ACD′=43°﹣25°=18°,
故答案为:18°或112°.
23.解:(1)由题意可得AB=AD,
∴∠ADB=∠B=50°,
∵DE⊥AD,
∴∠ADE=90°,
∴∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣50°﹣90°=40°,
∵∠C=28°,
∴∠AED=∠EDC+∠C=40°+28°=68°;
(2)∵AB=AD,点F是BD的中点,
∴AF⊥BD,∠BAF=∠DAF,
∴∠DAF+∠ADB=90°
∵DE⊥AD,
∴∠ADE=90°,
∴∠ADF+∠EDC=90°,
∴∠DAF=∠EDC,
∴∠BAF=∠EDC.
24.解:(1)图形如图1所示:
(2)解:如图1中,设直线l交PP′于C,
∵P′,P关于直线l对称,过点A的直线l垂直于线段BP所在的直线,
∴AC⊥PP′,CP=CP′,
∴AP=AP′,
∴∠APP′=∠AP′B,
又∵在△ABP中,∠B=60°,∠BAP=α,
∴∠AP′B=∠APP′=∠B+∠BAP=60°+α.
(3)如图2中,结论:PA=PM,PA与PM所成锐角为60°.
理由:设直线l交PP′于C,AB交MP′于D.
∵B,B′关于直线l对称
∴AC⊥BB′,CB=CB′,
∴AB=AB′,
∵∠B=60°,
∴∠B=∠B′=60°,
在△AP′B′中∠2=∠B′+∠3=60°+∠3,
又∵∠2=60°+α,
∴∠3=α,
∵P′,M关于AB′对称,
∴AB′⊥P′M,DP′=DM,
∴AP′=AM,
∴∠4=∠3=α,
∵∠5=α,
∴∠4=∠5,
∴∠PAM=∠PAB′+∠4=∠PAB′+∠5=∠BAB′,
∵AB=AB′,∠B=60°,
∴△BAB′为等边三角形,
∴∠BAB′=∠PAM=60°,
又∵由(2)得AP=AP′,AP′=AM,
∴AP=AM
∴△PAM为等边三角形
∴PA=PM,∠APM=60°,
即PA=PM,PA与PM所成角为60°.
25.解:(1)∠DAC的度数不会改变;
∵EA=EC,
∴∠EAC=∠C,①,
∵BA=BD,
∴∠BAD=∠BDA,
∵∠BAE=90°,
∴∠B=90°﹣∠AED=90°﹣2∠C,
∴∠BAD=(180°﹣∠B)=[180°﹣(90°﹣2∠C)]=45°+∠C,
∴∠DAE=90°﹣∠BAD=90°﹣(45°+∠C)=45°﹣∠C,②
由①,②得,∠DAC=∠DAE+∠CAE=45°﹣∠C+∠C=45°;
(2)设∠ABC=m°,
则∠BAD=(180°﹣m°)=90°﹣m°,∠AEB=180°﹣n°﹣m°,
∴∠DAE=n°﹣∠BAD=n°﹣90°+m°,
∵EA=EC,
∴∠CAE=AEB=90°﹣n°﹣m°,
∴∠DAC=∠DAE+∠CAE=n°﹣90°+m°+90°﹣n°﹣m°=n°.
26.解:(1)∵BO、CO分别平分∠ABC和∠ACB,
∵∠ABC=60°,∠ACB=40°
∴∠OBC=30°,∠OCB=20°,
∴∠COB=180°﹣(30°+20°)=130°;
(2)过O作OD⊥AB于D点,OE⊥AC于E,OF⊥BC于F,连接AO,如图,
∵∠ABC=60°,OB=4
∴∠OBD=30°,
∴OD=OB=2,
∵∠ABC和∠ACB的平分线相交于点O,
∴OE=OF=OD=2,
∵S△ABC=S△AOB+S△AOC+S△BOC
=×2×AB+×2×AC+×2×BC
=AB+BC+AC,
又∵△ABC的周长为16,
∴S△ABC=16.
27.解:(1)∵AD⊥BC,
∴∠ADB=90°,
∵∠ABC=40°,BE平分∠ABC,
∴∠DBF=∠ABC=20°,
∴∠BFD=90°﹣20°=70°,
∴∠AFE=∠BFD=70°;
(2)∵AE=AF,
∴∠AEF=∠AFE,
∵∠ABE=∠DBE,∠AFE=∠BFD,
∴∠BAE=180°﹣∠ABE﹣∠AEB,∠BDF=180°﹣∠DBF﹣∠BFD,
∴∠BAE=∠BDF=90°,
∴△ABC是直角三角形.
28.解:(1)∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积=DF?AC=×2×4=4.
29.解:(1)∵△ABC中,BA=BC,∠ABC=50°,
∴∠BAC=∠ACB=,
∵CB平分∠ACE,
∴∠BCE=∠ACB=65°,
∴∠DCE=180°﹣65°﹣65°=50°;
(2)∵△ABC中,BA=BC,
∴∠BAC=∠ACB,
∵CB平分∠ACE,
∴∠BCE=∠ACB
∴∠BCE=∠BAC,
∵∠ABC=∠DBE,
∴∠ABD=∠CBE,
∵AB=BC,
∴△BAD≌△BCE(ASA),
∴AD=CE.
1.下列图案不是轴对称图形的是( )
A. B. C. D.
2.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是( )
A.AD⊥BC B.EF=FD C.BE=BD D.AE=AC
3.如图,在△ABC中,∠A=87°,∠ABC的平分线BD交AC于点D,E是BC中点,且DE⊥BC,那么∠C的度数为( )
A.16° B.28° C.31° D.62°
4.下列四个说法:
①等腰三角形的腰一定大于其腰上的高;②等腰三角形的两腰上的中线长相等;
③等腰三角形的高、中线、角平分线互相重合;
④等腰三角形的一边为5,另一边为10,则它的周长为20或25.
其中正确的个数为( )
A.1个 B.2 C.3 D.4
5.如图,在△ABC中,AC的垂直平分线交边AC于点D,交边BC于点E,连接AE.若AB=6,BC=9,则△ABE的周长为( )
A.24 B.21 C.18 D.15
6.如图,在等腰△ABC中,∠ABC=118°,AB的垂直平分线DE交AB于点D,交AC于点E,BC的垂直平分线PQ交BC于点P,交AC于点Q,连接BE,BQ,则∠EBQ=( )
A.65° B.60° C.56° D.50°
7.如图,在△ABC中,AB⊥AC,AB=3,BC=5,AC=4,EF垂直平分BC,点P为直线EF上的任意一点,则△ABP周长的最小值是( )
A.12 B.6 C.7 D.8
8.如图,在△ABC中,∠A=45°,∠B=60°,点D在边AB上,且BD=BC,连接CD,则∠ACD的大小为( )
A.30° B.25° C.15° D.10°
9.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形可以画出( )
A.6个 B.5个 C.4个 D.3个
10.如图,在三角形纸片ABC中,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为( )
A.50° B.118° C.100° D.90°
11.如图,BE⊥AC于点D,且AB=BC,BD=ED,若∠ABC=54°,则∠E=( )
A.27° B.36° C.40° D.54°
12.在△ABC中,AB=5,BC=8,AC=6,AD平分∠BAC,则S△ABD:S△ACD= .
13.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若DE=2,BC=7,S△ABC=12,则AB的长为 .
14.如图,线段AB、BC的垂直平分线l1、l2相交于点O.若∠B=39°,则∠AOC= °.
15.如图所示的三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD.则BE= ,△ADE的周长等于 .
16.如图,在2×2的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC为格点三角形,在图中最多能画出 个不同的格点三角形与△ABC成轴对称.
17.若等腰三角形的一条边长为5cm,另一条边长为10cm,则此三角形第三条边长为 cm.
18.如图,在△ABC中,∠BAC=124°,分别作AC,AB两边的垂直平分线PM,PN,垂足分别是点M,N.以下说法正确的是 (填序号).
①∠P=56°;②∠EAF=68°;③PE=PF;④点P到点B和点C的距离相等.
19.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE= .
20.如图,在△ABC中,∠BAC=90°,点D在BC上,AB=AC,BD=BA,点E在BC的延长线上,CA=CE,连接AE,则∠DAE的度数为 °.
21.如图,在△ABC中,AB的垂直平分线DE分别与AB、BC交于点D、E,AC的垂直平分线FG分别与BC、AC交于点F、G,BC=10,EF=3,则△AEF的周长是 .
22.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=86°,则∠CAD的度数是 .
23.如图,在△ABC中,AB<AC<BC,以点A为圆心,线段AB的长为半径画弧,与BC边交于点D,连接AD过点D作DE⊥AD,交AC于点E.
(1)若∠B=50°,∠C=28°,求∠AED度数;
(2)若点F是BD的中点,连接AF,求证:∠BAF=∠EDC.
24.如图,在△ABP中,∠ABP=60°,90°<∠APB<120°,过点A的直线l垂直于线段BP所在的直线.设点B,P关于直线l的对称点分别为点B′,P′
(1)在图中画出△ABP关于直线l对称的三角形△AB′P′.
(2)若∠BAP=α,求∠AP′B的度数.(用α表示)
(3)若点P′关于直线AB′的对称点为M,连接AM,PM.请写出PA、PM之间的数量关系和位置关系,并证明你的结论.
25.问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由.
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
26.在△ABC中,∠ABC和∠ACB的平分线相交于点O,
(1)若∠ABC=60°,∠ACB=40°,求∠BOC的度数;
(2)若∠ABC=60°,OB=4,且△ABC的周长为16,求△ABC的面积.
27.阅读:在同一个三角形中,相等的边所对的角相等,简称为“等边对等角”.
例如,在△ABC中,如果AB=AC,依据“等边对等角”可得∠B=∠C.
请运用上述知识,解决问题:
已知:如图,△ABC中,AD⊥BC于D,BE是三角形的角平分线,交AD于F.
(1)若∠ABC=40°,求∠AFE的度数.
(2)若AE=AF,试判断△ABC的形状,并写出证明过程.
28.已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
29.如图,△ABC中,BA=BC,点D是AC延长线上一点,平面上一点E,连接EB、EC、ED、BD,CB平分∠ACE.
(1)若∠ABC=50°,求∠DCE的度数;
(2)若∠ABC=∠DBE,求证:AD=CE.
参考答案
1.解:A、不是轴对称图形,故此选项符合题意;
B、是轴对称图形,故此选项不合题意;
C、是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项不符合题意;
故选:A.
2.解:∵△ABC是等边三角形,△AED是等边三角形,
∴AB=AC=BC,∠BAC=60°,AE=AD=ED,∠EAD=60°,
∴∠DAB=∠DAC=30°,
∴AD⊥BC,故①正确,∠EAB=∠BAD=30°,
∴AB⊥ED,EF=DF,故②正确
∴BE=BD,故③正确,
无法得出AC=AE,故④错误;故选:D.
3.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE⊥BC,E是BC中点,
∴DB=DC,
∴∠DBC=∠C,
∴∠ABD=∠CBD=∠C,
∴∠ABD+∠CBD+∠C=180°﹣87°,
解得,∠C=31°,故选:C.
4.解:如图1,
在Rt△ABC中,AC=BC=BD,
∴等腰三角形的腰一定大于或等于其腰上的高,故①错误;
如图2,∵AB=AC,AD=DC,AE=EB,
∴DC=BE,∠DCB=∠EBC.
在△BDC和△CEB中,
,
∴△BDC≌△CEB(SAS).
∴BD=CE,故②正确;
∵等腰三角形的顶角的平分线,底边上的高,底边上的中线互相重合,故③错误;
∵等腰三角形的一边长为5,一边长为10,
∴只能三边是10,10,5,
∴它的周长是25,故④错误.
故选:A.
5.解:∵DE是线段AC的垂直平分线,
∴EA=EC,
∴△ABE的周长=AB+BE+EA=AB+BE+EC=AB+BC,
∵AB=6,BC=9,
∴△ABE的周长=AB+BC=6+9=15,
故选:D.
6.解:等腰△ABC中,∠ABC=118°,
∴∠A=∠C=31°,
∵AB的垂直平分线DE交AB于点D,交AC于点E,BC的垂直平分线PQ交BC于点P,交AC于点Q,
∴EA=EB,QB=QC,
∴∠ABE=∠QBC=∠A=∠C=31°,
∴∠EBQ=∠ABC﹣∠ABE﹣∠QBC=118°﹣31°﹣31°=56°,
故选:C.
7.解:∵EF垂直平分BC,
∴B、C关于EF对称,
设AC交EF于D,
∴当P和D重合时,AP+BP的值最小,最小值等于AC的长,
∵AB=3,AC=4,
∴△ABP周长的最小值是AB+AC=3+4=7.
故选:C.
8.解:在△ABC中,∠A=45°,∠B=60°,
∴∠ACB=180°﹣45°﹣60°=75°,
∵BD=BC,
∴∠BCD=(180°﹣60°)÷2=60°,
∴∠ACD=∠ACB﹣∠BCD=75°﹣60°=15°.
故选:C.
9.解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故选:A.
10.解:在△ABC中,∠A=60°,∠B=70°,
∴∠C=180°﹣∠A﹣∠B=50°.
由折叠,可知:∠CDE=∠C′DE,∠CED=∠C′ED,
∴∠CED==99°,
∴∠CDE=180°﹣∠CED﹣∠C=31°,
∴∠1=180°﹣∠CDE﹣∠C′DE=180°﹣2∠CDE=118°.
故选:B.
11.解:∵AB=BC,BE⊥AC,∠ABC=54°,
∴∠CBD=∠ABD=∠ABC=27°,
∵BE⊥AC,BD=ED,
∴AC是BE的垂直平分线,
∴CB=CE,
∴∠E=∠CBD=27°.
故选:A.
12.解:过D作DE⊥AB于E,DF⊥AC于F,
∵AD平分∠BAC,
∴DE=DF,
设DE=DF=R,
∵S△ABD==R,S△ACD==,
∴S△ABD:S△ACD=5:6,
故答案为:5:6.
13.解:
过D作DF⊥BA,交BA的延长线于F,
∵BD平分∠ABC,DE⊥BC,DE=2,
∴DF=DE=2,
∵BC=7,S△ABC=S△ABD+S△BDC=12,
∴+=12,
∴=12,
解得:AB=5,
故答案为:5.
14.解:连接BO并延长至D,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴OA=OB,OC=OB,
∴∠OAB=∠OBA,∠OCB=∠OBC,
∴∠AOD=2∠OBA,∠COD=2∠OBC,
∴∠AOC=2(∠OBA+∠OBC)=2∠ABC=78°,
故答案为:78.
15.解:∵折叠这个三角形点C落在AB边上的点E处,折痕为BD,
∴BE=BC=6cm,DE=CD,
∴AE=AB﹣BE=AB﹣BC=8﹣6=2(cm),
∴△ADE的周长=AD+DE+AE,=AD+CD+AE,=AC+AE,=5+2,=7(cm).
故答案为:6cm;7cm.
16.解:与△ABC成轴对称的格点三角形如图所示,
在图中最多能画出5个不同的格点三角形与△ABC成轴对称.
故答案为:5.
17.解:当5cm为底时,其它两边都为10cm,
则5cm、10cm、10cm可以构成三角形;
当5cm为腰时,其它两边为5cm和10cm,因为5+5=10,所以不能构成三角形,故舍去.
所以三角形三边长只能是5cm、10cm、10cm,所以第三边是10cm.
故答案为:10.
18.解:∵PM垂直平分AC,PN垂直平分AB,
∴∠PMA=∠PNA=90°,
∴∠P=360°﹣90°﹣90°﹣124°=56°,①说法正确;
∵∠BAC=124°,
∴∠B+∠C=180°﹣124°=56°,
∵PM垂直平分AC,PN垂直平分AB,
∴EC=EA,FB=FA,
∴∠EAC=∠C,∠FAB=∠B,
∴∠EAF=∠BAC﹣∠EAC﹣∠FAB=∠BAC﹣(∠B+∠C)=124°﹣56°=68°,②说法正确;
△ABC不一定是等腰三角形,
∴PE与PF的大小无法确定,③说法错误;
连接PC、PA、PB,
∵PM垂直平分AC,PN垂直平分AB,
∴PC=PA,PB=PA,
∴PB=PC,即点P到点B和点C的距离相等,④说法正确,
故答案为:①②④.
19.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
20.解:∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=(180°﹣∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E=∠ACB=22.5°,
在△ABE中,∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=112.5°﹣67.5°=45°,
故答案为:45.
21.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
同理,FA=FC,
∴△AEF的周长=FA+EF+EA=EB+EF+FC=BC+EF+EF=16,
故答案为:16.
22.解:∵C、D两点在线段AB的中垂线上,
∴CA=CB,DA=DB,
∵CD⊥AB,
∴∠ACD=∠ACB=×50°=25°,∠ADC=∠ADB=×86°=43°,
当点C与点D在线段AB两侧时,∠CAD=180°﹣∠ACD﹣∠ADC=180°﹣25°﹣43°=112°,
当点C与点D′在线段AB同侧时,∠CAD′=∠AD′C﹣∠ACD′=43°﹣25°=18°,
故答案为:18°或112°.
23.解:(1)由题意可得AB=AD,
∴∠ADB=∠B=50°,
∵DE⊥AD,
∴∠ADE=90°,
∴∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣50°﹣90°=40°,
∵∠C=28°,
∴∠AED=∠EDC+∠C=40°+28°=68°;
(2)∵AB=AD,点F是BD的中点,
∴AF⊥BD,∠BAF=∠DAF,
∴∠DAF+∠ADB=90°
∵DE⊥AD,
∴∠ADE=90°,
∴∠ADF+∠EDC=90°,
∴∠DAF=∠EDC,
∴∠BAF=∠EDC.
24.解:(1)图形如图1所示:
(2)解:如图1中,设直线l交PP′于C,
∵P′,P关于直线l对称,过点A的直线l垂直于线段BP所在的直线,
∴AC⊥PP′,CP=CP′,
∴AP=AP′,
∴∠APP′=∠AP′B,
又∵在△ABP中,∠B=60°,∠BAP=α,
∴∠AP′B=∠APP′=∠B+∠BAP=60°+α.
(3)如图2中,结论:PA=PM,PA与PM所成锐角为60°.
理由:设直线l交PP′于C,AB交MP′于D.
∵B,B′关于直线l对称
∴AC⊥BB′,CB=CB′,
∴AB=AB′,
∵∠B=60°,
∴∠B=∠B′=60°,
在△AP′B′中∠2=∠B′+∠3=60°+∠3,
又∵∠2=60°+α,
∴∠3=α,
∵P′,M关于AB′对称,
∴AB′⊥P′M,DP′=DM,
∴AP′=AM,
∴∠4=∠3=α,
∵∠5=α,
∴∠4=∠5,
∴∠PAM=∠PAB′+∠4=∠PAB′+∠5=∠BAB′,
∵AB=AB′,∠B=60°,
∴△BAB′为等边三角形,
∴∠BAB′=∠PAM=60°,
又∵由(2)得AP=AP′,AP′=AM,
∴AP=AM
∴△PAM为等边三角形
∴PA=PM,∠APM=60°,
即PA=PM,PA与PM所成角为60°.
25.解:(1)∠DAC的度数不会改变;
∵EA=EC,
∴∠EAC=∠C,①,
∵BA=BD,
∴∠BAD=∠BDA,
∵∠BAE=90°,
∴∠B=90°﹣∠AED=90°﹣2∠C,
∴∠BAD=(180°﹣∠B)=[180°﹣(90°﹣2∠C)]=45°+∠C,
∴∠DAE=90°﹣∠BAD=90°﹣(45°+∠C)=45°﹣∠C,②
由①,②得,∠DAC=∠DAE+∠CAE=45°﹣∠C+∠C=45°;
(2)设∠ABC=m°,
则∠BAD=(180°﹣m°)=90°﹣m°,∠AEB=180°﹣n°﹣m°,
∴∠DAE=n°﹣∠BAD=n°﹣90°+m°,
∵EA=EC,
∴∠CAE=AEB=90°﹣n°﹣m°,
∴∠DAC=∠DAE+∠CAE=n°﹣90°+m°+90°﹣n°﹣m°=n°.
26.解:(1)∵BO、CO分别平分∠ABC和∠ACB,
∵∠ABC=60°,∠ACB=40°
∴∠OBC=30°,∠OCB=20°,
∴∠COB=180°﹣(30°+20°)=130°;
(2)过O作OD⊥AB于D点,OE⊥AC于E,OF⊥BC于F,连接AO,如图,
∵∠ABC=60°,OB=4
∴∠OBD=30°,
∴OD=OB=2,
∵∠ABC和∠ACB的平分线相交于点O,
∴OE=OF=OD=2,
∵S△ABC=S△AOB+S△AOC+S△BOC
=×2×AB+×2×AC+×2×BC
=AB+BC+AC,
又∵△ABC的周长为16,
∴S△ABC=16.
27.解:(1)∵AD⊥BC,
∴∠ADB=90°,
∵∠ABC=40°,BE平分∠ABC,
∴∠DBF=∠ABC=20°,
∴∠BFD=90°﹣20°=70°,
∴∠AFE=∠BFD=70°;
(2)∵AE=AF,
∴∠AEF=∠AFE,
∵∠ABE=∠DBE,∠AFE=∠BFD,
∴∠BAE=180°﹣∠ABE﹣∠AEB,∠BDF=180°﹣∠DBF﹣∠BFD,
∴∠BAE=∠BDF=90°,
∴△ABC是直角三角形.
28.解:(1)∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积=DF?AC=×2×4=4.
29.解:(1)∵△ABC中,BA=BC,∠ABC=50°,
∴∠BAC=∠ACB=,
∵CB平分∠ACE,
∴∠BCE=∠ACB=65°,
∴∠DCE=180°﹣65°﹣65°=50°;
(2)∵△ABC中,BA=BC,
∴∠BAC=∠ACB,
∵CB平分∠ACE,
∴∠BCE=∠ACB
∴∠BCE=∠BAC,
∵∠ABC=∠DBE,
∴∠ABD=∠CBE,
∵AB=BC,
∴△BAD≌△BCE(ASA),
∴AD=CE.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
