2020--2021学年沪科版八年级下册16.1 二次根式教学同步课件(26张ppt)
文档属性
| 名称 | 2020--2021学年沪科版八年级下册16.1 二次根式教学同步课件(26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 374.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 12:12:22 | ||
图片预览







文档简介
(共26张PPT)
第16章
二次根式
16.1
二次根式
知识回顾
用带有根号的式子填空,看看写出的结果有什么特点:
(1)面积为3的正方形的边长为
,面积为S的正方形的边长为_____.
(2)一个长方形的围栏,长是宽的2倍,面积为130
m2,则它的宽为______m.
(3)一个物体从高处自由落下,落到地面所用的时间t(单位:s)
与开始落下时离地面的高度h(单位:m)满足关系h=5t2.如果用含有h的式子表示t,那么t为______.
获取新知
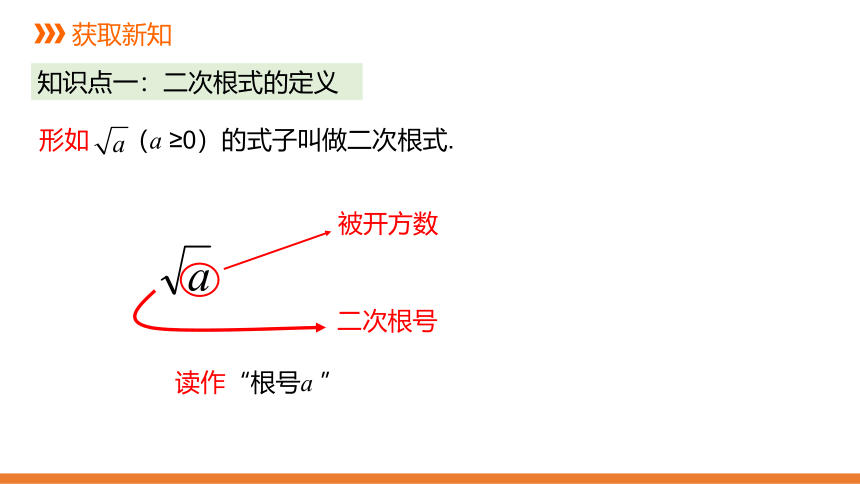
形如
(a
≥0)的式子叫做二次根式.
被开方数
二次根号
读作“根号a
”
知识点一:二次根式的定义
两个必备特征
①外貌特征:含有“
”
②内在特征:被开方数a
≥0
注意:a可以是数,也可以是式.
例题讲解
例1
下列各式中,哪些是二次根式?哪些不是?
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
分析:
解:(1)(4)(6)均是二次根式,其中a2+1属于“非负数+正数”的形式一定大于零.
(2)(3)(5)(7)均不是二次根式.
例2
当x为何值时,下列式子在实数范围内有意义?
解:(1)要使
有意义,必须x+3
≥0.解这个不等
式,得
x
≥
-3.
即当x
≥
-3时,
在实数范围内有意义.
(2)因为x为任何实数时都有x2
≥0,所以当x为一切实数时,
在实数范围内都有意义
求二次根式有意义时字母的取值范围的方法:
第一步,明确式子有意义的条件,对于单个的二次根式,
只需满足被开方数为非负数;
对于含有多个二次根式的,则必须满足多个被开方数
同时为非负数;
对于零指数幂,则必须满足底数不能为零
获取新知
当a>0时,
表示a的算术平方根,因此
>0;
当a=0时,
表示0的算术平方根,因此
=0.
这就是说,当a≥0时,
≥0.
知识点二:二次根式的性质1
问题
二次根式
的被开方数a的取值范围是什么?它本身的取值范围又是什么?
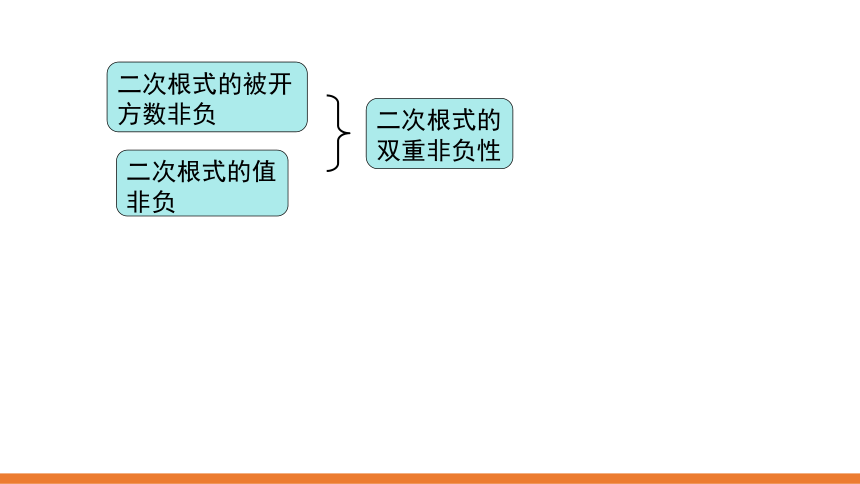
二次根式的被开方数非负
二次根式的值非负
二次根式的双重非负性
根据算术平方根及平方的意义填空,你发现了什么?
a(a≥0)
...
算术平方根
平方运算
4
5
0
...
...
22
=
4
02
=
0
观察两者有什么关系?
归纳总结
的性质:
一般地,
=a
(a
≥0).
即一个非负数的算术平方根的平方等于它本身.
注意:
不要忽略a≥0这一限制条件.
这是使二次根式有意义的前提条件.
例题讲解
例3
计算:
解:
积的乘方:
(ab)2=a2b2
获取新知
知识点三:二次根式的性质2
根据算术平方根意义填空,你发现了什么?
平方运算
算术平方根
a(a≥0)
3
0.5
0
-0.5
...
观察两者有什么关系?
归纳总结
即任意一个非负数的平方的算术平方根等于它本身的绝对值.
的性质:
a
(a≥0)
-a
(a<0)
例题讲解
例4
计算:
(1)
;
(2)
.
解:
(1)
或
(2)
例5
先化简再求值:
,其中x=4.
解:
当x=4时,
∴当x=4时,
计算
一般有两个步骤:①去掉根号及被开方数
的指数,写成绝对值的形式,即
=|a|;②去掉绝对
值符号,根据绝对值的意义进行化简,即|a|=
随堂演练
1.
下列式子中,不属于二次根式的是(
)
C
2.
如果式子
有意义,那么x的取值范围在数轴上表示正确的是( )
C
3.
下列等式正确的是( )
A
4.当x=____时,二次根式
取最小值,其最小值为____.
-1
0
-1
0
1
2
a
5.
实数a在数轴上的位置如图所示,化简
的结果是
.
1
6.
实数a、b在数轴上的对应点如图所示,请你化简:
a
b
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
7.
已知a、b、c是△ABC的三边长,化简:
解:∵a、b、c是△ABC的三边长,
∴a+b+c>0,b+c>a,b+a>c,
∴原式=|a+b+c|-|b+c-a|+|c-b-a|
=a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
=3a+b-c.
8.先化简,再求值:当a=9时,求
的值,甲、乙两人的解答如下:
甲的解答:原式=
乙的解答:原式=
当a=9时,|1-a|=a-1,所以原式=a+a-1=2a-1=17.
两人的解答中谁的解答是错误的?请你说明错误的原因.
解:甲的解答是错误的.
错误原因:∵当a=9时,1-a<0,
课堂小结
二次根式性质
二次根式
定义
带有二次根号
在有意义条件下求字母的取值范围
抓住被开方数必须为非负数,从而建立不等式求出其解集.
被开方数为非负数
(a为全体实数)
第16章
二次根式
16.1
二次根式
知识回顾
用带有根号的式子填空,看看写出的结果有什么特点:
(1)面积为3的正方形的边长为
,面积为S的正方形的边长为_____.
(2)一个长方形的围栏,长是宽的2倍,面积为130
m2,则它的宽为______m.
(3)一个物体从高处自由落下,落到地面所用的时间t(单位:s)
与开始落下时离地面的高度h(单位:m)满足关系h=5t2.如果用含有h的式子表示t,那么t为______.
获取新知
形如
(a
≥0)的式子叫做二次根式.
被开方数
二次根号
读作“根号a
”
知识点一:二次根式的定义
两个必备特征
①外貌特征:含有“
”
②内在特征:被开方数a
≥0
注意:a可以是数,也可以是式.
例题讲解
例1
下列各式中,哪些是二次根式?哪些不是?
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
分析:
解:(1)(4)(6)均是二次根式,其中a2+1属于“非负数+正数”的形式一定大于零.
(2)(3)(5)(7)均不是二次根式.
例2
当x为何值时,下列式子在实数范围内有意义?
解:(1)要使
有意义,必须x+3
≥0.解这个不等
式,得
x
≥
-3.
即当x
≥
-3时,
在实数范围内有意义.
(2)因为x为任何实数时都有x2
≥0,所以当x为一切实数时,
在实数范围内都有意义
求二次根式有意义时字母的取值范围的方法:
第一步,明确式子有意义的条件,对于单个的二次根式,
只需满足被开方数为非负数;
对于含有多个二次根式的,则必须满足多个被开方数
同时为非负数;
对于零指数幂,则必须满足底数不能为零
获取新知
当a>0时,
表示a的算术平方根,因此
>0;
当a=0时,
表示0的算术平方根,因此
=0.
这就是说,当a≥0时,
≥0.
知识点二:二次根式的性质1
问题
二次根式
的被开方数a的取值范围是什么?它本身的取值范围又是什么?
二次根式的被开方数非负
二次根式的值非负
二次根式的双重非负性
根据算术平方根及平方的意义填空,你发现了什么?
a(a≥0)
...
算术平方根
平方运算
4
5
0
...
...
22
=
4
02
=
0
观察两者有什么关系?
归纳总结
的性质:
一般地,
=a
(a
≥0).
即一个非负数的算术平方根的平方等于它本身.
注意:
不要忽略a≥0这一限制条件.
这是使二次根式有意义的前提条件.
例题讲解
例3
计算:
解:
积的乘方:
(ab)2=a2b2
获取新知
知识点三:二次根式的性质2
根据算术平方根意义填空,你发现了什么?
平方运算
算术平方根
a(a≥0)
3
0.5
0
-0.5
...
观察两者有什么关系?
归纳总结
即任意一个非负数的平方的算术平方根等于它本身的绝对值.
的性质:
a
(a≥0)
-a
(a<0)
例题讲解
例4
计算:
(1)
;
(2)
.
解:
(1)
或
(2)
例5
先化简再求值:
,其中x=4.
解:
当x=4时,
∴当x=4时,
计算
一般有两个步骤:①去掉根号及被开方数
的指数,写成绝对值的形式,即
=|a|;②去掉绝对
值符号,根据绝对值的意义进行化简,即|a|=
随堂演练
1.
下列式子中,不属于二次根式的是(
)
C
2.
如果式子
有意义,那么x的取值范围在数轴上表示正确的是( )
C
3.
下列等式正确的是( )
A
4.当x=____时,二次根式
取最小值,其最小值为____.
-1
0
-1
0
1
2
a
5.
实数a在数轴上的位置如图所示,化简
的结果是
.
1
6.
实数a、b在数轴上的对应点如图所示,请你化简:
a
b
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
7.
已知a、b、c是△ABC的三边长,化简:
解:∵a、b、c是△ABC的三边长,
∴a+b+c>0,b+c>a,b+a>c,
∴原式=|a+b+c|-|b+c-a|+|c-b-a|
=a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
=3a+b-c.
8.先化简,再求值:当a=9时,求
的值,甲、乙两人的解答如下:
甲的解答:原式=
乙的解答:原式=
当a=9时,|1-a|=a-1,所以原式=a+a-1=2a-1=17.
两人的解答中谁的解答是错误的?请你说明错误的原因.
解:甲的解答是错误的.
错误原因:∵当a=9时,1-a<0,
课堂小结
二次根式性质
二次根式
定义
带有二次根号
在有意义条件下求字母的取值范围
抓住被开方数必须为非负数,从而建立不等式求出其解集.
被开方数为非负数
(a为全体实数)
