2020--2021学年八年级数学沪科版下册教学同步课件:19.2 第3课时 平行四边形的判定(共21张ppt)
文档属性
| 名称 | 2020--2021学年八年级数学沪科版下册教学同步课件:19.2 第3课时 平行四边形的判定(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 199.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 12:27:27 | ||
图片预览






文档简介
(共21张PPT)
第19章
四边形
19.2
第3课时
平行四边形的判定
知识回顾
1.回顾:平行四边形的性质
平行四边形对边平行;
平行四边形对边相等;
平行四边形对角相等;
平行四边形对角线互相平分
2.思考:平行四边形的性质的逆命题
对边平行的四边形是平行四边形;
对边相等的四边形是平行四边形;
对角相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形
猜:这些逆命题可否成为平行四边形的判定方法?
获取新知
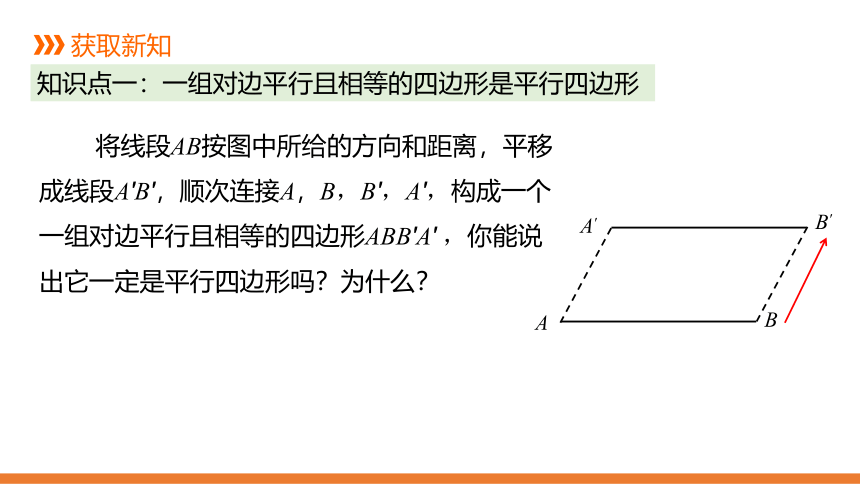
知识点一:一组对边平行且相等的四边形是平行四边形
将线段AB按图中所给的方向和距离,平移成线段A′B′,顺次连接A,B,B′,A′,构成一个一组对边平行且相等的四边形ABB′A′
,你能说出它一定是平行四边形吗?为什么?
A
B
A'
B'
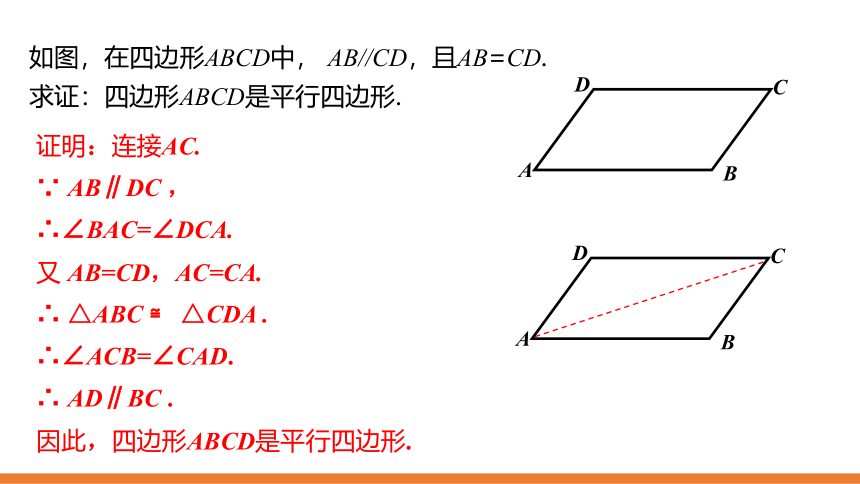
如图,在四边形ABCD中,
AB//CD,且AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵
AB∥DC
,
∴∠BAC=∠DCA.
又
AB=CD,AC=CA.
∴
△ABC
≌
△CDA
.
∴∠ACB=∠CAD.
∴
AD∥BC
.
因此,四边形ABCD是平行四边形.
D
A
B
C
D
A
B
C
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
归纳总结
符号语言描述:
在四边形ABCD中,
∵AB
CD,
∴四边形ABCD是平行四边形.
B
D
A
C
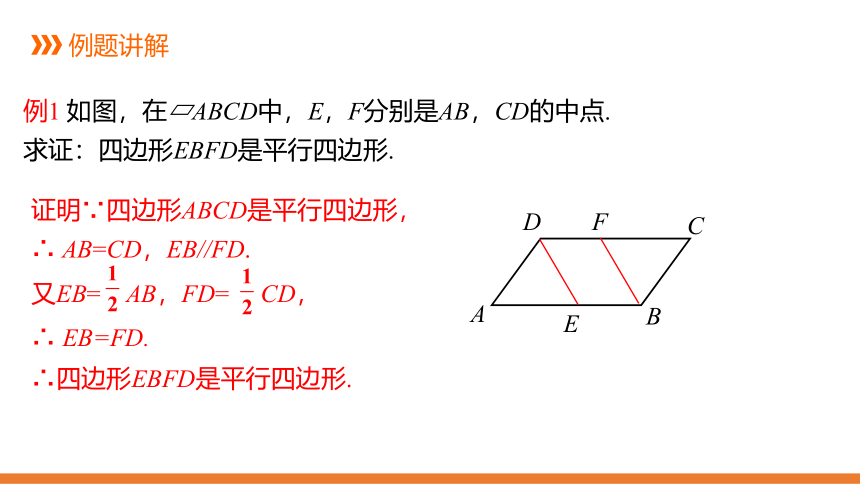
例1
如图,在?ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
例题讲解
证明∵四边形ABCD是平行四边形,
∴
AB=CD,EB//FD.
又EB=
AB,FD=
CD,
∴
EB=FD.
∴四边形EBFD是平行四边形.
B
D
A
C
E
F
获取新知
知识点二:两组对边相等的四边形是平行四边形
已知:
四边形ABCD中,AB=DC,AD=BC.
求证:
四边形ABCD是平行四边形.
证明:∵AB=CD,AD=CB,AC=CA,
∴△ABC≌△CDA,
∴∠1=∠2,∠3=∠4,
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
归纳总结
符号语言描述:
在四边形ABCD中,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
B
D
A
C
例题讲解
例2
如图,在Rt△MON中,∠MON=90°.
求证:四边形PONM是平行四边形.
证明:Rt△MON中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
获取新知
知识点三:对角线互相平分的四边形是平行四边形
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:∵OA=OC,OD=OB,∠AOD=∠COB,
∴△
AOD≌△COB.
∴∠OAD=∠OCB,∠ODA=∠OBC.
∴AD//BC,AB//DC.
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
对角线互相平分的四边形是平行四边形.
归纳总结
符号语言描述:
在四边形ABCD中,
∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
B
O
D
A
C
例题讲解
例3
已知:如图,点E,F是?ABCD的对角线AC上两点,且AE=CF.
求证:四边形BEDF是平行四边形.
证明:连接BD交AC于点O.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵AE=CF,
∴OE=AO
-AE=CO
-CF=OF.
∴四边形BEDF是平行四边形.
B
D
A
C
E
F
O
随堂演练
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
2
四边形的四条边长分别是a,b,c,d,其中a,b为一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
B
3.如图,在四边形ABCD中,如果∠A:∠B:∠
C:∠D
=a:b:a:b(a,b为正数),那么四边形ABCD是__________.
平行四边形
4.
横格纸的横线是互相平行的,在一条横线上截取线段
AB=
25
mm,在另一条横线上按照同一方向截取CD=25
mm,连结AC,BD,那么四边形ACDB一定是平行四边形,
理由是____________________________________________
一组对边平行且相等的四边形是平行四边形
5.如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
证明:∵△ABD、△BCE、△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,
∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,
∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.
6.如图,在四边形ABCD中,AB=CD,过点A作AE⊥BD交BD于点E,过点C作CF⊥BD交BD于点F,且AE=CF.
求证:四边形ABCD是平行四边形.
证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
在Rt△ABE和Rt△CDF中,
∵AE=CF,AB=CD,
∴Rt△ABE≌Rt△CDF,
∴∠ABE=∠CDF,
∴AB∥CD.
∵AB=CD,
∴四边形ABCD是平行四边形.
7.
如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?
说说你的理由.
解:四边形BMDN是平行四边形.
理由如下:连接BD交AC于O.
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°.
∵四边形ABCD是平行四边形,
∴OB=OD,AO=CO,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∴△ADN≌△CBM,∴AN=CM,
∴OA-AN=OC-CM,即ON=OM,
∴四边形BMDN是平行四边形.
O
课堂小结
平行四边形的判定
定义法:两组对边分别平行
对边:两组对边分别相等
对角:两组对角分别相等
对角线:对角线互相平分
一组对边平行且相等
定义的拓展
第19章
四边形
19.2
第3课时
平行四边形的判定
知识回顾
1.回顾:平行四边形的性质
平行四边形对边平行;
平行四边形对边相等;
平行四边形对角相等;
平行四边形对角线互相平分
2.思考:平行四边形的性质的逆命题
对边平行的四边形是平行四边形;
对边相等的四边形是平行四边形;
对角相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形
猜:这些逆命题可否成为平行四边形的判定方法?
获取新知
知识点一:一组对边平行且相等的四边形是平行四边形
将线段AB按图中所给的方向和距离,平移成线段A′B′,顺次连接A,B,B′,A′,构成一个一组对边平行且相等的四边形ABB′A′
,你能说出它一定是平行四边形吗?为什么?
A
B
A'
B'
如图,在四边形ABCD中,
AB//CD,且AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵
AB∥DC
,
∴∠BAC=∠DCA.
又
AB=CD,AC=CA.
∴
△ABC
≌
△CDA
.
∴∠ACB=∠CAD.
∴
AD∥BC
.
因此,四边形ABCD是平行四边形.
D
A
B
C
D
A
B
C
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
归纳总结
符号语言描述:
在四边形ABCD中,
∵AB
CD,
∴四边形ABCD是平行四边形.
B
D
A
C
例1
如图,在?ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
例题讲解
证明∵四边形ABCD是平行四边形,
∴
AB=CD,EB//FD.
又EB=
AB,FD=
CD,
∴
EB=FD.
∴四边形EBFD是平行四边形.
B
D
A
C
E
F
获取新知
知识点二:两组对边相等的四边形是平行四边形
已知:
四边形ABCD中,AB=DC,AD=BC.
求证:
四边形ABCD是平行四边形.
证明:∵AB=CD,AD=CB,AC=CA,
∴△ABC≌△CDA,
∴∠1=∠2,∠3=∠4,
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
归纳总结
符号语言描述:
在四边形ABCD中,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
B
D
A
C
例题讲解
例2
如图,在Rt△MON中,∠MON=90°.
求证:四边形PONM是平行四边形.
证明:Rt△MON中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
获取新知
知识点三:对角线互相平分的四边形是平行四边形
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:∵OA=OC,OD=OB,∠AOD=∠COB,
∴△
AOD≌△COB.
∴∠OAD=∠OCB,∠ODA=∠OBC.
∴AD//BC,AB//DC.
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
对角线互相平分的四边形是平行四边形.
归纳总结
符号语言描述:
在四边形ABCD中,
∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
B
O
D
A
C
例题讲解
例3
已知:如图,点E,F是?ABCD的对角线AC上两点,且AE=CF.
求证:四边形BEDF是平行四边形.
证明:连接BD交AC于点O.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵AE=CF,
∴OE=AO
-AE=CO
-CF=OF.
∴四边形BEDF是平行四边形.
B
D
A
C
E
F
O
随堂演练
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
2
四边形的四条边长分别是a,b,c,d,其中a,b为一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
B
3.如图,在四边形ABCD中,如果∠A:∠B:∠
C:∠D
=a:b:a:b(a,b为正数),那么四边形ABCD是__________.
平行四边形
4.
横格纸的横线是互相平行的,在一条横线上截取线段
AB=
25
mm,在另一条横线上按照同一方向截取CD=25
mm,连结AC,BD,那么四边形ACDB一定是平行四边形,
理由是____________________________________________
一组对边平行且相等的四边形是平行四边形
5.如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
证明:∵△ABD、△BCE、△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,
∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,
∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.
6.如图,在四边形ABCD中,AB=CD,过点A作AE⊥BD交BD于点E,过点C作CF⊥BD交BD于点F,且AE=CF.
求证:四边形ABCD是平行四边形.
证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
在Rt△ABE和Rt△CDF中,
∵AE=CF,AB=CD,
∴Rt△ABE≌Rt△CDF,
∴∠ABE=∠CDF,
∴AB∥CD.
∵AB=CD,
∴四边形ABCD是平行四边形.
7.
如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?
说说你的理由.
解:四边形BMDN是平行四边形.
理由如下:连接BD交AC于O.
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°.
∵四边形ABCD是平行四边形,
∴OB=OD,AO=CO,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∴△ADN≌△CBM,∴AN=CM,
∴OA-AN=OC-CM,即ON=OM,
∴四边形BMDN是平行四边形.
O
课堂小结
平行四边形的判定
定义法:两组对边分别平行
对边:两组对边分别相等
对角:两组对角分别相等
对角线:对角线互相平分
一组对边平行且相等
定义的拓展
