代入法方解二元一次程组

(共18张PPT)
——用代入法解二元一次方程组
（第1课时）
解二元一次方程组
课前五分钟训练
1、若　　　是方程５ｘ＋ｋｙ＝４的解，则ｋ＝　　。
试一试你能行
-3
2你能把下列方程写成用含x的式子表示y的形式吗？
用含ｘ的式子表示ｙ为___________
用含ｙ的式子表示ｘ为_______________.
3.已知二元一次方程2x+y=4
y=4-2x
并比较哪一种形式简单？
哼!我从你背上拿来1个，我的包裹数就是你的2倍！
你还累？这么大的个，才比我多驮了2个．
它们各驮了多少包裹呢？
真的？
用一元一次方程求解
解：小马驮了x个包裹，则老牛驮了（x+2)个包裹，根据题意，得：
解：设小马驮了 x 个包裹,老牛驮了y个包裹, 根据题意，得：
用二元一次方程组求解
解得：x=5.
将x=5代入得x+2=7
答：老牛驮了7个包裹，小马驮了5个包裹。
用一元一次方程求解
解：小马驮了x个包裹，则老牛驮了（x+2)个包裹，根据题意，得：
解：设小马驮了 x 个包裹,老牛驮了y个包裹, 根据题意，得：
用二元一次方程组求解
解得：x=5.
将x=5代入得x+2=7
答：老牛驮了7个包裹，小马驮了5个包裹。
观察:列二元一次方程组和列一元一次方程设未知数有何不同？列出的方程和方程组又有何联系？对你解二元一次方程组有何启示？
分析
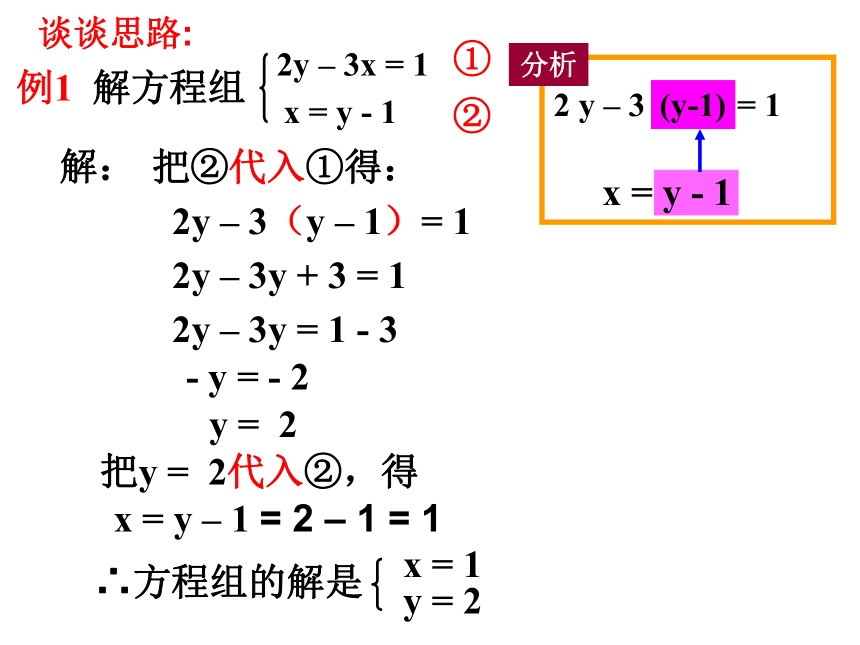
例1 解方程组
2y – 3x = 1
x = y - 1
解：
①
②
把②代入①得：
2y – 3（y – 1）= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②，得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路:
例1 解方程组
2y – 3x = 1
x = y - 1
①
②
变：
2y – 3x = 1
x – y = – 1
①
②
谈谈思路:
解：
把②代入①得：
2y – 3（y – 1）= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②，得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
例2 解方程组
解：
①
②
由①得：
x = 3+ y
③
把③代入②得：
3（3+y）– 8y= 14
把y= – 1代入③，得
x = 2
1、将方程组里的一个方程变形，用含有一个未知数的式子表示另一个未知数；
2、用这个式子代替另一个方程中相应的未知数，得到一个一元一次方程，求得一个未知数的值；
3、把这个未知数的值代入上面的式子，求得另一个未知数的值；
4、写出方程组的解。
上面解二元一次方程组基本思路是什么？ 一般步骤有哪些？
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法:
解二元一次方程组
⑴
y=2x-3
3x+2y=8
⑵
2x- y=5
3x +4y=2
能 力 检 验
1.教材随堂练习
2.补充练习：用代入消元法解下列方程组
自己编2-3个二元一次方程组并用代入法把它们解出来。
1、二元一次方程组
这节课我们学习了
什么知识
代入消元法
一元一次方程
2、代入消元法的一般步骤：
3、思想方法：转化思想、代入消元思想、
方程（组）思想.
知 识 梳 理
变
代
求
写
1
1 . 已知 是二元一次方程组
的解，则 a= ，b= 。
2.已知 (a+2b-5)2+|4a+b-6|=0， 求a和b的值.
知 识 拓 展
3
1
bx+ay = 5
ax+by = 7
a=1
b=1
思考题
3.若方程组
2x-y=3
3x+2y=8
的解与方程组
ax+by=1
bx+3y=a
的解相同,求a,b的值.
1、练习：解方程组
看看你掌握了吗？
2、已知（2x+3y- 4）+∣x+3y-7∣=0
则x= ，y= 。
2
－3
解：由②得,y =－1－4x ③
把③代入①得,2x－3(－1－4x )= 7
解得,x=
把x= 代入③得 y=－1－4× =
∴原方程组的解为
①
②
解:由①得, ③
把③代入②得,
解得,
把 代入③得,
∴原方程组的解为
小结:
通过本节课的研究,学习,你有哪些收获？
基本思路:
消元: 二元
一元
主要步骤：
变形技巧：
用含一个未知数的代数式表示另一个未知数；代入另一个方程消去一个元；分别求
出两个未知数的值；写出方程组的解。
选择系数比较简单的方程进行变形。
巩 固 延 伸
请写出一个二元一次方程组，
使它的解是
x = 7
y = 1
2x-5y=9
2x+5y=19
3x+4y=25
5x+2y=37
1