青岛版七年级下册第9章角全章学案(无答案)
文档属性
| 名称 | 青岛版七年级下册第9章角全章学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 184.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-12 13:21:47 | ||
图片预览



文档简介
七年级数学第9章《角》学案
§9.1 角的表示
主备人:新泰羊流初级中学 郭玲
【教师寄语】“学而不思则惘,思而不学则殆”,只有在学习中不断思考才能不断地进步.
【学习目标】1、掌握角的两种定义及有关概念;
2、掌握角的四种表示方法;
3、提高抽象、概括能力及操作实践能力.
【重难点】1、角的两种定义表示法;2、角的四种表示法.
【课前预习】
1、角的两种定义表示法:(1) ;(2) .
2、角的四种表示法:(1) ;(2) ;
(3) ;(4) .
【学习过程】
一、自主学习
1、角的定义
观察:秒针在钟面上转动;
操作:把圆规的两只脚由并在一起到逐渐把一只脚旋转到另一个位置;
思考:在秒针的转动过程中,有没有给我们形成角的形象?那么角又可以是怎样形成的呢?
小结:角是具有 的两条射线组成的图形。其中,组成角的两条射线叫做角的两条 ,公共端点叫做角的 .
2、角的表示方法:
试结合图形来说明角的四种表示方法:
⑴用一个角的符号∠,加上三个 表示.例如,∠
⑵用一个角的符号∠,加上表示顶点的一个 表示.例如,∠
⑶用一个角的符号∠,加上一个 字母表示.例如,∠
⑷用一个角的符号∠,加上一个 表示.例如,∠
合作交流
1、举例说明什么是角的始边?角的终边?(组内交流)
2、小结:角是由一条射线绕着它的端点旋转到另一个位置所成的图形,处于 位置的那条射线叫做角的始边, 位置的那条射线叫做角的终边.
3、当始边和终边处于同一条直线上时,这时构成的角是 ;当终边旋转回到始边位置,并与始边重合,这时,所构成的角是 .
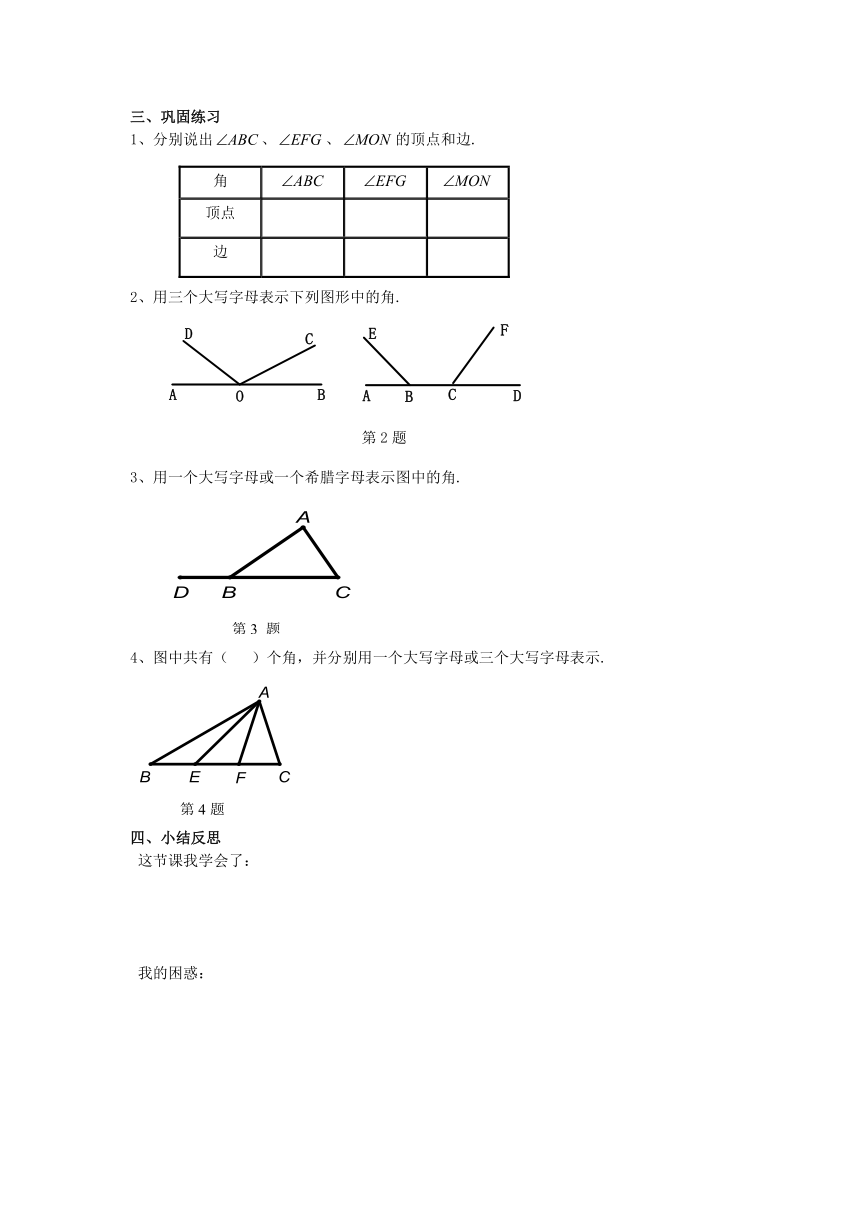
三、巩固练习
1、分别说出、、的顶点和边.
角
顶点
边
2、用三个大写字母表示下列图形中的角.
3、用一个大写字母或一个希腊字母表示图中的角.
4、图中共有( )个角,并分别用一个大写字母或三个大写字母表示.
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
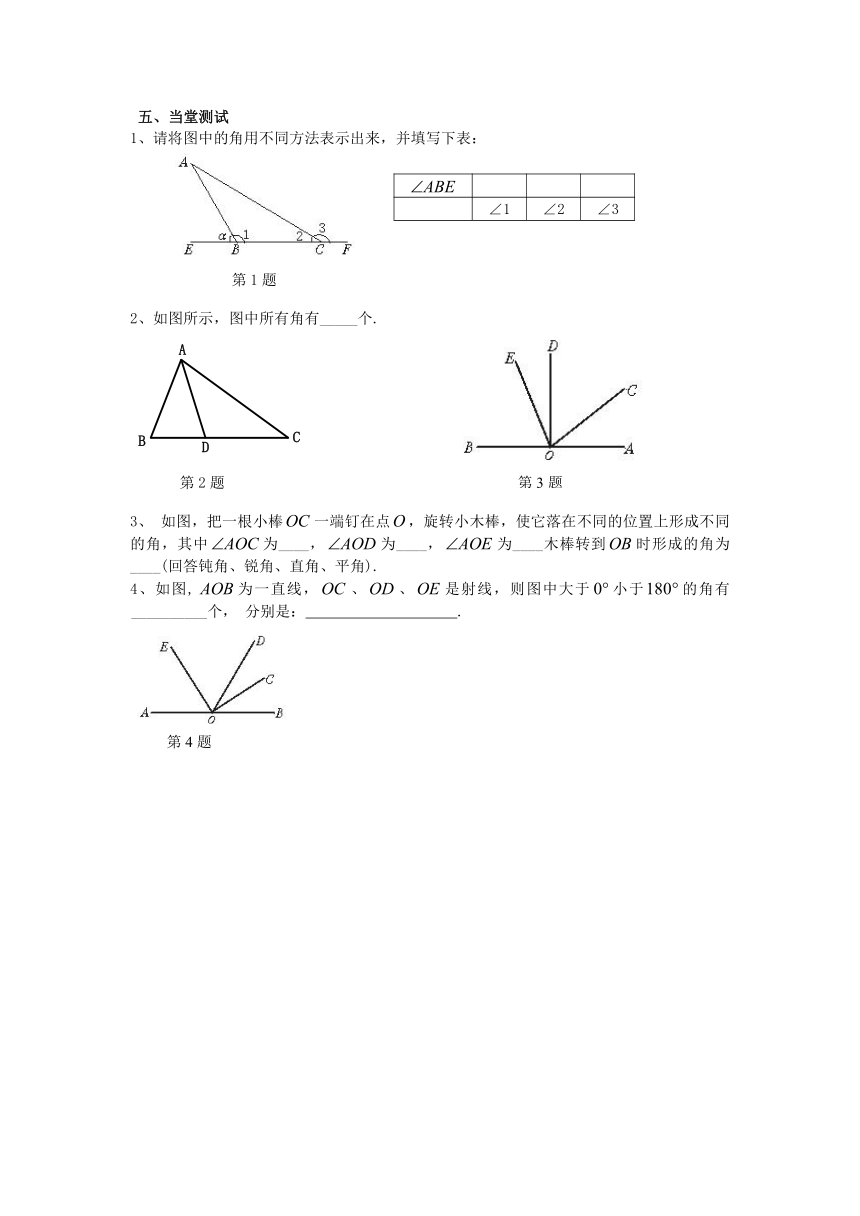
1、请将图中的角用不同方法表示出来,并填写下表:
∠1 ∠2 ∠3
2、如图所示,图中所有角有_____个.
3、 如图,把一根小棒一端钉在点,旋转小木棒,使它落在不同的位置上形成不同的角,其中为____,为____,为____木棒转到时形成的角为____(回答钝角、锐角、直角、平角).
4、如图,为一直线,、、是射线,则图中大于小于的角有__________个, 分别是: .
§9.2 角的比较
主备人:新泰羊流初级中学 郭玲
【教师寄语】自信是走向成功的第一步!
【学习目标】
1、理解角的大小比较意义;掌握直角、锐角、钝角的概念;掌握角平分线的概念.
2、会估计一个角的大小;会用叠合法和度量法进行角的大小比较;会区别直角、锐角和钝角;会运用角平分线的性质解决一些角的计算问题.
3、体验生活中的几何知识,激发学生对生活的热爱;通过动脑、动手、动口、合作和探究,启发学生的智慧,感受快乐数学,接受逻辑推理思维的熏陶.
【重难点】角的大小比较和角平分线的概念.
【课前预习】 比较角的大小.
如图1,两块三角尺的顶点分别记为、、和、、.你认为与哪个角较大?说说你是怎样比较的?
【学习过程】
自主学习
1、估计角的大小
叠合法:如图2,把一个角放在另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在这一边的同侧. 此时,边落在内部,这就说明小于,记作<或>.
如果两个角的顶点和它们的两边都能分别重合,我们就说这两个角相等.
度量法:比较角的大小,我们也可以用量角器分别量出角的度数,然后加以比较.
例如∵,,∴<.
2、试一试:
根据两块三角板(如图1)上各个角的度数,在“=”、“>”或“<”中,选择适当的符号填入下面的各空格内:
___,,,,.
3、做一做:
在一张透明纸上任意画一个角(如
图3),把这张透明纸折叠,使角的两边与
重合,然后把这张纸展开、铺平,画出折
痕.
试比较与的大小.
角的平分线:从一个角的顶点引出的一条射线,
把这个角分成两个相等的角,这条射线叫做这个角的平分线(angular bisector).
例如:图3中射线就是的平分线,这时.
4、想一想:怎样用量角器画一个角的平分线?
如图4,已知,画射线,使平分.
5、练一练:(仿照例2)
如图5,,,平分.求的度数.
解:
小结:一般地,一个角的度数是另两个角的度数的和,这个角就是另两个角的和.一个角的度数是另两个角的度数的差,这个角就是另两个角的差.
二、合作交流
利用一副三角尺,你能画出哪些度数的角?
三、巩固练习
1、比较下列各题中两个角的大小.
(1) (2)
2、根据图形填空:
(1);(2);
(3).
3、已知是,你可以用哪些方法画出的平分线?
4、如图,点在直线上,画出的平分线.若,求的度数.
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
1、3∶30时,时针与分针所成的角是( ).
A.锐角 B.直角 C.钝角 D.平角
2、填“>”或“<”.
(1)直角 锐角,直角 钝角,钝角 锐角,直角 钝角 平角.
(2)如图1,
∠AOC ∠AOB
∠BOD ∠COD
∠AOC ∠AOD
∠BOD ∠BOC
3、看图2填空:
(1).
(2)若,,则,若,,,则,.
(3) =,.
4、如图3,为直线上一点,平分,
平分,则;
若,则,,
,.
5、如图,∠AOB是平角,OD、OC、OE是三条射线,OD是∠AOC的平分线, 请你补充一个条使∠DOE=90°,并说明你的理由.
§9.3 角的度量
主备人:新泰羊流初级中学 郭玲
【教师寄语】在探究中求知,在合作中解疑,展示自我,相信自己!
【学习目标】1、认识度、分、秒,会进行它们之间的简单换算,会通过角度比较角的大小。
2、会用量角器度量一个角的大小,并判断它是直角、锐角还是钝角。
3、认知互为余角,互为补角 ,能利用互余角互补角进行计算.
4、余角性质,补角性质 ,能利用余角性质、补角性质解决问题.
【重难点】1、互为余角,互为补角. 2、余角性质,补角性质.
【课前预习】
1、什么叫互为余角?余角的性质? .
2、什么叫互为补角?补角的性质? .
3、若,,则与_______;若,,则与_________;若,则与________;若,则与________;若,且,则与_______.
若,则与互为补角,对吗?
4、互为余角的两个角必是_________.
互为补角的两个角中能是两直角?两钝角?两锐角?
5、与互余,则=________ ,与互补,则=________.
【学习过程】
一、自主学习
1、角的度量单位之间的关系
把圆周分成360份,每一份是1度记作1°,1周角=360°;
把1度分成60份,每一份是1分记作1′,1°=60′;
把1分分成60份,每一份是1秒记作1″,1′=60″
2、角的分类:
(1)特殊的角:
用一副三角板可画出哪些角(不大于180°):直接画:30°、45°、60°、90°;间接画:15°、75°、105°、120°、135°、150°、165°、180°
绕着端点旋转到角的终边和始边成一直线,这时所成的角叫做平角;
绕着端点旋转到角的终边和始边再次重合,这时所成的角叫做周角。
(2)小于180°角可以分成:锐角、直角、钝角
例1 把18°15′化成用度表示的角。
解:
思考18°15′与18.15°是否相等 并说明理由。
例2 ∠α=37°50′∠β=52°10′
求 ∠α+∠β与 ∠β-∠α
3、认知互为余角,互为补角
若,则和互为余角,是的余角,是的余角.
若∠1+∠2=180°,则∠1与∠2互为补角,∠1是∠2是补角,∠2是∠1的补角.
例3、如图,如果与互余, 与互余,那么与相等吗 为什么
解: 与相等.
∵与互余, 与互余,
∴,,(余角的定义)
∴.(等量代换)
想一想:如果与互补, 与互余,,那么与有怎样的关系 为什么 (理解例题的说理过程,说明的过程及理由.)
2、题组训练:
(1)已知,,则.
(2)若,则它的余角是_______,它的补角是________.
(3)若一个角有补角但没有余角这个角是__________.
(4)一个角的补角是它余角的3倍,则这个角是_____.
二、合作交流
补角性质与余角性质
例4、如果∠1与∠2互补,∠3与∠4互补,且∠1=∠3,那么∠2与∠4相等吗?为什么?
补角性质:同角或等角的补角相等. 余角性质:同角或等角的余角相等.
三、巩固练习
1、判断题
(1)一个锐角与一个钝角的和一定大于平角. ( )
(2)一个角一定小于它的余角,也小于它的补角. ( )
(3)如果两个角互补,则它们的角平分线互相垂直. ( )
(4)如两个角互补,则一个角为锐角,另一个为钝角. ( )
(5)互余的两个角的比是4:6,则这两个角分别是、 ( )
(6)如果,,,那么互为补角. ( )
(7)用一副三角板的内角可画出大于且小于不同度数的角共有11种. ( )
2、填空题
(1)若,,则.
(2)若,,且,则.
(3)若,,则.
(4)若,∠1+∠2=180°,且,则.
3、已知一个角的补角和这个角的余角互补,求这个角的度数.
4、如图, ,图中有与互补的角吗
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
1、计算:
(1)49°38′+66°22′; (2)180°-79°19′;
2、,则其余角为_______,补角为_______.
3、的补角是70°,则=__________.
4、一个角的补角与它的余角的2倍的和是平角 ,则这个角是______.
5、一个锐角的补角与它的余角的差为________.
6、一个角的补角是这个角的余角的5倍,求这个角_______.
§9.4 对顶角
主备人:新泰羊流初级中学 郭玲
【教师寄语】善于珍惜时间的人就等于延长了生命.
【学习目标】1、理解对顶角的概念,能在图形中辨认;
2、掌握对顶角相等的性质和它的推证过程;
3、会用对顶角的性质进行有关的推理和计算.
【重难点】1、对顶角的正确判断.2、对顶角相等的应用,写出简单的证明过程.
【课前预习】
1、如果,则与是______.
2、已知,是的邻补角,则=_______.
3、如图,是的角平分线,
,则=_______.
4、与互为补角,与也互
为补角,则_______.
【学习过程】
一、自主学习
对顶角定义:
(1)指出的边和顶点.
(2)把,延长,得到,,
形成,观察这两个角,它们有什么特点?
(3)总结:
对顶角的定义: .
于是我们在上图中可得到:∠ 与∠ 是对顶角,∠ 与∠ 是对顶角.
二、合作交流(对顶角相等)
1、操作:每个同学画一对对顶角,分别量出它们的度数.
猜想:下图中,= ,.(为什么?)
结论:如果两个角是对顶角,那么这两个角 .简单的说: 相等.
如图,直线与相交于点,射线是角的平分线,已知,求,,,的度数.
三、巩固练习
1、说出下列图中的对顶角.
2、已知:直线与直线相交于, ,求,,各为多少度?
解:
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
如图: , ,那么,=____,=____,=_____,=___.
2、已知:直线、相交于点,平分,,求.
3、直、相交于点,,如果,那么等于多少度?
§9.5 垂直
主备人:新泰羊流初级中学 郭玲
【教师寄语】好问,是好的.但是如果自己不想,只随口问,即使能得到正确答复,也未必受到大益.所以学问二字,“问”放在“学”的后面.
【学习目标】1、通过画、折等活动,认识两条直线互相垂直及垂线的概念,掌握有关的符号表示.
2、会借助三角尺、量角器等画垂线,进一步丰富操作活动经验.
3、通过操作活动,探索有关垂直的一些性质,体会点到直线距离
【学习重点】1、垂直的定义;
2、通过动手画垂直的两条直线,探索有关垂直的一些性质.
【学习难点】垂线的画法.
【课前预习】
1、平面内的两条直线有哪几种位置关系?
2、收集有垂直的图案或物品.
【学习过程】
一、自主学习(垂直的定义)
1.(动手做一做)将一张长方形的纸对折,量一量折痕与纸边所成角的度数.
2.你能说一说什么叫垂直吗?
只要两条直线相交成 角,就说这两条直线互相垂直.其中一条直线是另一条直线的 ,它们的交点叫做 .
如图,直线AB与直线CD相交成直角,
我们就说直线AB与直线CD互相 ,
直线AB是直线CD的 ,直线CD也是
直线AB的 .交点O是 .
3.垂直的表示
垂直用符号 表示,直线与直线互相垂直,记作 或 读作 .如果垂足是,那么可记作: 或 .在垂足处常打上直角标志“”以便运用和识别.如果用l、m表示这两条直线,那么直线l与m垂直,记作: .
大家要注意:两条线段或射线垂直是指这两条线段或射线所在的直线垂直.
4.思考:互相垂直的两条直线形成的四个角都是直角,你是如何得出的?
二.合作交流
(一)垂线的画法
1、探索画垂线的方法:(1)利用三角尺作出两条互相垂直的直线.(2)用量角器画垂线.
(3)用方格纸画垂线,有几种画法?在这些方法中,你认为哪一种比较简单呢?
2.直线与点有哪几种位置关系?
在下图中过点A作l的垂线,你能作出多少条?
3、归纳操作要点
画这条直线的垂线的方法,分为三步:
一靠:即把三角尺的一条直角边靠在已知直线上.
二移:即移动三角尺使三角尺的另一条直角边经过已知点.
三画:即沿已知点所在的直角边画出直线.
通过画图,得出垂线的性质:在平面内,过一点(这一点可以在直线上,也可以在直线外)只能作一条直线与已知直线垂直.
(二)垂线段性质
如图,从P点出发向直线m所作的线段中哪一条最短?你怎么知道的?
从以上的两个活动中得出垂线的另一性质:直线外一点与直线上各点连接的所有线段中,垂线段最短.
(三)点到直线的距离
如下图,如何测量跳远成绩?请学生上来演示.
得出:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
三、巩固练习
1、找出图中互相垂直的线段.
2、判断
1)一条直线的垂线只能画一条. ( )
2)两直线相交所构成的四个角相等,则这两直线互相垂直. ( )
3)点到直线的垂线段就是点到直线的距离. ( )
4)过一点有且只有一条直线与已知直线垂直. ( )
3、如图,,且,则为( ).
A. B.
C. D.
4、如图,是的边上一点.
(1)过点画的垂线,交于点;(2)过点画的垂线,垂足为.
5、思考:要把水渠中的水引到村庄,(1)在渠岸的什么地方开沟,才能使水沟最短,画出图形,并说明道理.(2)若河另一侧有村庄,问怎样架桥,才能使到距离最近.
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
1、点到直线的距离是指这点到这条直线的( ).
A.垂线段 B.垂线 C.垂线的长度 D.垂线段的长度
2、已知,且∶=2∶3,则的度数是( ).
A.30 ° B.150° C.30°或150° D.不能确定
3、如图中的与满足_____________条件时,能使.(只要添一个条件即可)
4、如图,将一副三角板叠放在一起,使直角的顶点重合于点,则__________.
第2题
第3 题
第4题
第1题
第3题
第2题
第4题
图3
图4
图5
第1题
O
图3
第3 题
A
B
C
D
O
1
2
3
4
第2题
第1题
第2题
第1题
第3 题
m
第3题
第4 题
第5 题图
·D
·C
A
·
·
·
·
····
B
第3 题
第4 题
§9.1 角的表示
主备人:新泰羊流初级中学 郭玲
【教师寄语】“学而不思则惘,思而不学则殆”,只有在学习中不断思考才能不断地进步.
【学习目标】1、掌握角的两种定义及有关概念;
2、掌握角的四种表示方法;
3、提高抽象、概括能力及操作实践能力.
【重难点】1、角的两种定义表示法;2、角的四种表示法.
【课前预习】
1、角的两种定义表示法:(1) ;(2) .
2、角的四种表示法:(1) ;(2) ;
(3) ;(4) .
【学习过程】
一、自主学习
1、角的定义
观察:秒针在钟面上转动;
操作:把圆规的两只脚由并在一起到逐渐把一只脚旋转到另一个位置;
思考:在秒针的转动过程中,有没有给我们形成角的形象?那么角又可以是怎样形成的呢?
小结:角是具有 的两条射线组成的图形。其中,组成角的两条射线叫做角的两条 ,公共端点叫做角的 .
2、角的表示方法:
试结合图形来说明角的四种表示方法:
⑴用一个角的符号∠,加上三个 表示.例如,∠
⑵用一个角的符号∠,加上表示顶点的一个 表示.例如,∠
⑶用一个角的符号∠,加上一个 字母表示.例如,∠
⑷用一个角的符号∠,加上一个 表示.例如,∠
合作交流
1、举例说明什么是角的始边?角的终边?(组内交流)
2、小结:角是由一条射线绕着它的端点旋转到另一个位置所成的图形,处于 位置的那条射线叫做角的始边, 位置的那条射线叫做角的终边.
3、当始边和终边处于同一条直线上时,这时构成的角是 ;当终边旋转回到始边位置,并与始边重合,这时,所构成的角是 .
三、巩固练习
1、分别说出、、的顶点和边.
角
顶点
边
2、用三个大写字母表示下列图形中的角.
3、用一个大写字母或一个希腊字母表示图中的角.
4、图中共有( )个角,并分别用一个大写字母或三个大写字母表示.
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
1、请将图中的角用不同方法表示出来,并填写下表:
∠1 ∠2 ∠3
2、如图所示,图中所有角有_____个.
3、 如图,把一根小棒一端钉在点,旋转小木棒,使它落在不同的位置上形成不同的角,其中为____,为____,为____木棒转到时形成的角为____(回答钝角、锐角、直角、平角).
4、如图,为一直线,、、是射线,则图中大于小于的角有__________个, 分别是: .
§9.2 角的比较
主备人:新泰羊流初级中学 郭玲
【教师寄语】自信是走向成功的第一步!
【学习目标】
1、理解角的大小比较意义;掌握直角、锐角、钝角的概念;掌握角平分线的概念.
2、会估计一个角的大小;会用叠合法和度量法进行角的大小比较;会区别直角、锐角和钝角;会运用角平分线的性质解决一些角的计算问题.
3、体验生活中的几何知识,激发学生对生活的热爱;通过动脑、动手、动口、合作和探究,启发学生的智慧,感受快乐数学,接受逻辑推理思维的熏陶.
【重难点】角的大小比较和角平分线的概念.
【课前预习】 比较角的大小.
如图1,两块三角尺的顶点分别记为、、和、、.你认为与哪个角较大?说说你是怎样比较的?
【学习过程】
自主学习
1、估计角的大小
叠合法:如图2,把一个角放在另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在这一边的同侧. 此时,边落在内部,这就说明小于,记作<或>.
如果两个角的顶点和它们的两边都能分别重合,我们就说这两个角相等.
度量法:比较角的大小,我们也可以用量角器分别量出角的度数,然后加以比较.
例如∵,,∴<.
2、试一试:
根据两块三角板(如图1)上各个角的度数,在“=”、“>”或“<”中,选择适当的符号填入下面的各空格内:
___,,,,.
3、做一做:
在一张透明纸上任意画一个角(如
图3),把这张透明纸折叠,使角的两边与
重合,然后把这张纸展开、铺平,画出折
痕.
试比较与的大小.
角的平分线:从一个角的顶点引出的一条射线,
把这个角分成两个相等的角,这条射线叫做这个角的平分线(angular bisector).
例如:图3中射线就是的平分线,这时.
4、想一想:怎样用量角器画一个角的平分线?
如图4,已知,画射线,使平分.
5、练一练:(仿照例2)
如图5,,,平分.求的度数.
解:
小结:一般地,一个角的度数是另两个角的度数的和,这个角就是另两个角的和.一个角的度数是另两个角的度数的差,这个角就是另两个角的差.
二、合作交流
利用一副三角尺,你能画出哪些度数的角?
三、巩固练习
1、比较下列各题中两个角的大小.
(1) (2)
2、根据图形填空:
(1);(2);
(3).
3、已知是,你可以用哪些方法画出的平分线?
4、如图,点在直线上,画出的平分线.若,求的度数.
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
1、3∶30时,时针与分针所成的角是( ).
A.锐角 B.直角 C.钝角 D.平角
2、填“>”或“<”.
(1)直角 锐角,直角 钝角,钝角 锐角,直角 钝角 平角.
(2)如图1,
∠AOC ∠AOB
∠BOD ∠COD
∠AOC ∠AOD
∠BOD ∠BOC
3、看图2填空:
(1).
(2)若,,则,若,,,则,.
(3) =,.
4、如图3,为直线上一点,平分,
平分,则;
若,则,,
,.
5、如图,∠AOB是平角,OD、OC、OE是三条射线,OD是∠AOC的平分线, 请你补充一个条使∠DOE=90°,并说明你的理由.
§9.3 角的度量
主备人:新泰羊流初级中学 郭玲
【教师寄语】在探究中求知,在合作中解疑,展示自我,相信自己!
【学习目标】1、认识度、分、秒,会进行它们之间的简单换算,会通过角度比较角的大小。
2、会用量角器度量一个角的大小,并判断它是直角、锐角还是钝角。
3、认知互为余角,互为补角 ,能利用互余角互补角进行计算.
4、余角性质,补角性质 ,能利用余角性质、补角性质解决问题.
【重难点】1、互为余角,互为补角. 2、余角性质,补角性质.
【课前预习】
1、什么叫互为余角?余角的性质? .
2、什么叫互为补角?补角的性质? .
3、若,,则与_______;若,,则与_________;若,则与________;若,则与________;若,且,则与_______.
若,则与互为补角,对吗?
4、互为余角的两个角必是_________.
互为补角的两个角中能是两直角?两钝角?两锐角?
5、与互余,则=________ ,与互补,则=________.
【学习过程】
一、自主学习
1、角的度量单位之间的关系
把圆周分成360份,每一份是1度记作1°,1周角=360°;
把1度分成60份,每一份是1分记作1′,1°=60′;
把1分分成60份,每一份是1秒记作1″,1′=60″
2、角的分类:
(1)特殊的角:
用一副三角板可画出哪些角(不大于180°):直接画:30°、45°、60°、90°;间接画:15°、75°、105°、120°、135°、150°、165°、180°
绕着端点旋转到角的终边和始边成一直线,这时所成的角叫做平角;
绕着端点旋转到角的终边和始边再次重合,这时所成的角叫做周角。
(2)小于180°角可以分成:锐角、直角、钝角
例1 把18°15′化成用度表示的角。
解:
思考18°15′与18.15°是否相等 并说明理由。
例2 ∠α=37°50′∠β=52°10′
求 ∠α+∠β与 ∠β-∠α
3、认知互为余角,互为补角
若,则和互为余角,是的余角,是的余角.
若∠1+∠2=180°,则∠1与∠2互为补角,∠1是∠2是补角,∠2是∠1的补角.
例3、如图,如果与互余, 与互余,那么与相等吗 为什么
解: 与相等.
∵与互余, 与互余,
∴,,(余角的定义)
∴.(等量代换)
想一想:如果与互补, 与互余,,那么与有怎样的关系 为什么 (理解例题的说理过程,说明的过程及理由.)
2、题组训练:
(1)已知,,则.
(2)若,则它的余角是_______,它的补角是________.
(3)若一个角有补角但没有余角这个角是__________.
(4)一个角的补角是它余角的3倍,则这个角是_____.
二、合作交流
补角性质与余角性质
例4、如果∠1与∠2互补,∠3与∠4互补,且∠1=∠3,那么∠2与∠4相等吗?为什么?
补角性质:同角或等角的补角相等. 余角性质:同角或等角的余角相等.
三、巩固练习
1、判断题
(1)一个锐角与一个钝角的和一定大于平角. ( )
(2)一个角一定小于它的余角,也小于它的补角. ( )
(3)如果两个角互补,则它们的角平分线互相垂直. ( )
(4)如两个角互补,则一个角为锐角,另一个为钝角. ( )
(5)互余的两个角的比是4:6,则这两个角分别是、 ( )
(6)如果,,,那么互为补角. ( )
(7)用一副三角板的内角可画出大于且小于不同度数的角共有11种. ( )
2、填空题
(1)若,,则.
(2)若,,且,则.
(3)若,,则.
(4)若,∠1+∠2=180°,且,则.
3、已知一个角的补角和这个角的余角互补,求这个角的度数.
4、如图, ,图中有与互补的角吗
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
1、计算:
(1)49°38′+66°22′; (2)180°-79°19′;
2、,则其余角为_______,补角为_______.
3、的补角是70°,则=__________.
4、一个角的补角与它的余角的2倍的和是平角 ,则这个角是______.
5、一个锐角的补角与它的余角的差为________.
6、一个角的补角是这个角的余角的5倍,求这个角_______.
§9.4 对顶角
主备人:新泰羊流初级中学 郭玲
【教师寄语】善于珍惜时间的人就等于延长了生命.
【学习目标】1、理解对顶角的概念,能在图形中辨认;
2、掌握对顶角相等的性质和它的推证过程;
3、会用对顶角的性质进行有关的推理和计算.
【重难点】1、对顶角的正确判断.2、对顶角相等的应用,写出简单的证明过程.
【课前预习】
1、如果,则与是______.
2、已知,是的邻补角,则=_______.
3、如图,是的角平分线,
,则=_______.
4、与互为补角,与也互
为补角,则_______.
【学习过程】
一、自主学习
对顶角定义:
(1)指出的边和顶点.
(2)把,延长,得到,,
形成,观察这两个角,它们有什么特点?
(3)总结:
对顶角的定义: .
于是我们在上图中可得到:∠ 与∠ 是对顶角,∠ 与∠ 是对顶角.
二、合作交流(对顶角相等)
1、操作:每个同学画一对对顶角,分别量出它们的度数.
猜想:下图中,= ,.(为什么?)
结论:如果两个角是对顶角,那么这两个角 .简单的说: 相等.
如图,直线与相交于点,射线是角的平分线,已知,求,,,的度数.
三、巩固练习
1、说出下列图中的对顶角.
2、已知:直线与直线相交于, ,求,,各为多少度?
解:
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
如图: , ,那么,=____,=____,=_____,=___.
2、已知:直线、相交于点,平分,,求.
3、直、相交于点,,如果,那么等于多少度?
§9.5 垂直
主备人:新泰羊流初级中学 郭玲
【教师寄语】好问,是好的.但是如果自己不想,只随口问,即使能得到正确答复,也未必受到大益.所以学问二字,“问”放在“学”的后面.
【学习目标】1、通过画、折等活动,认识两条直线互相垂直及垂线的概念,掌握有关的符号表示.
2、会借助三角尺、量角器等画垂线,进一步丰富操作活动经验.
3、通过操作活动,探索有关垂直的一些性质,体会点到直线距离
【学习重点】1、垂直的定义;
2、通过动手画垂直的两条直线,探索有关垂直的一些性质.
【学习难点】垂线的画法.
【课前预习】
1、平面内的两条直线有哪几种位置关系?
2、收集有垂直的图案或物品.
【学习过程】
一、自主学习(垂直的定义)
1.(动手做一做)将一张长方形的纸对折,量一量折痕与纸边所成角的度数.
2.你能说一说什么叫垂直吗?
只要两条直线相交成 角,就说这两条直线互相垂直.其中一条直线是另一条直线的 ,它们的交点叫做 .
如图,直线AB与直线CD相交成直角,
我们就说直线AB与直线CD互相 ,
直线AB是直线CD的 ,直线CD也是
直线AB的 .交点O是 .
3.垂直的表示
垂直用符号 表示,直线与直线互相垂直,记作 或 读作 .如果垂足是,那么可记作: 或 .在垂足处常打上直角标志“”以便运用和识别.如果用l、m表示这两条直线,那么直线l与m垂直,记作: .
大家要注意:两条线段或射线垂直是指这两条线段或射线所在的直线垂直.
4.思考:互相垂直的两条直线形成的四个角都是直角,你是如何得出的?
二.合作交流
(一)垂线的画法
1、探索画垂线的方法:(1)利用三角尺作出两条互相垂直的直线.(2)用量角器画垂线.
(3)用方格纸画垂线,有几种画法?在这些方法中,你认为哪一种比较简单呢?
2.直线与点有哪几种位置关系?
在下图中过点A作l的垂线,你能作出多少条?
3、归纳操作要点
画这条直线的垂线的方法,分为三步:
一靠:即把三角尺的一条直角边靠在已知直线上.
二移:即移动三角尺使三角尺的另一条直角边经过已知点.
三画:即沿已知点所在的直角边画出直线.
通过画图,得出垂线的性质:在平面内,过一点(这一点可以在直线上,也可以在直线外)只能作一条直线与已知直线垂直.
(二)垂线段性质
如图,从P点出发向直线m所作的线段中哪一条最短?你怎么知道的?
从以上的两个活动中得出垂线的另一性质:直线外一点与直线上各点连接的所有线段中,垂线段最短.
(三)点到直线的距离
如下图,如何测量跳远成绩?请学生上来演示.
得出:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
三、巩固练习
1、找出图中互相垂直的线段.
2、判断
1)一条直线的垂线只能画一条. ( )
2)两直线相交所构成的四个角相等,则这两直线互相垂直. ( )
3)点到直线的垂线段就是点到直线的距离. ( )
4)过一点有且只有一条直线与已知直线垂直. ( )
3、如图,,且,则为( ).
A. B.
C. D.
4、如图,是的边上一点.
(1)过点画的垂线,交于点;(2)过点画的垂线,垂足为.
5、思考:要把水渠中的水引到村庄,(1)在渠岸的什么地方开沟,才能使水沟最短,画出图形,并说明道理.(2)若河另一侧有村庄,问怎样架桥,才能使到距离最近.
四、小结反思
这节课我学会了:
我的困惑:
五、当堂测试
1、点到直线的距离是指这点到这条直线的( ).
A.垂线段 B.垂线 C.垂线的长度 D.垂线段的长度
2、已知,且∶=2∶3,则的度数是( ).
A.30 ° B.150° C.30°或150° D.不能确定
3、如图中的与满足_____________条件时,能使.(只要添一个条件即可)
4、如图,将一副三角板叠放在一起,使直角的顶点重合于点,则__________.
第2题
第3 题
第4题
第1题
第3题
第2题
第4题
图3
图4
图5
第1题
O
图3
第3 题
A
B
C
D
O
1
2
3
4
第2题
第1题
第2题
第1题
第3 题
m
第3题
第4 题
第5 题图
·D
·C
A
·
·
·
·
····
B
第3 题
第4 题
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
