17.2.1 平面直角坐标系(共35张ppt)
文档属性
| 名称 | 17.2.1 平面直角坐标系(共35张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 495.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 12:32:16 | ||
图片预览








文档简介
第17章 函数及其图象
17.2 函数的图象
第1课时 平面直角坐标系
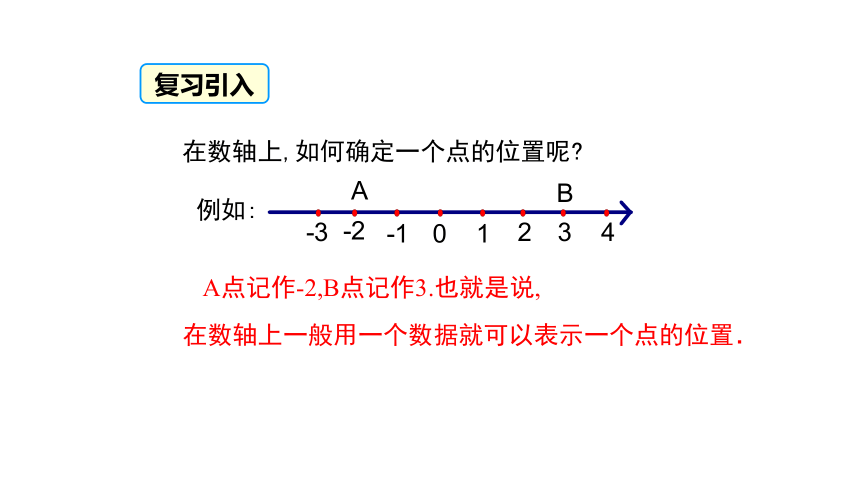
复习引入
在数轴上,如何确定一个点的位置呢?
A点记作-2,B点记作3.也就是说,
例如:
在数轴上一般用一个数据就可以表示一个点的位置.
小明父子俩周末去电影院看国产大片《战狼2》,买了两张票去观看,座位号分别是3排6座和6排3座.怎样才能既快又准地找到座位?
情境引入
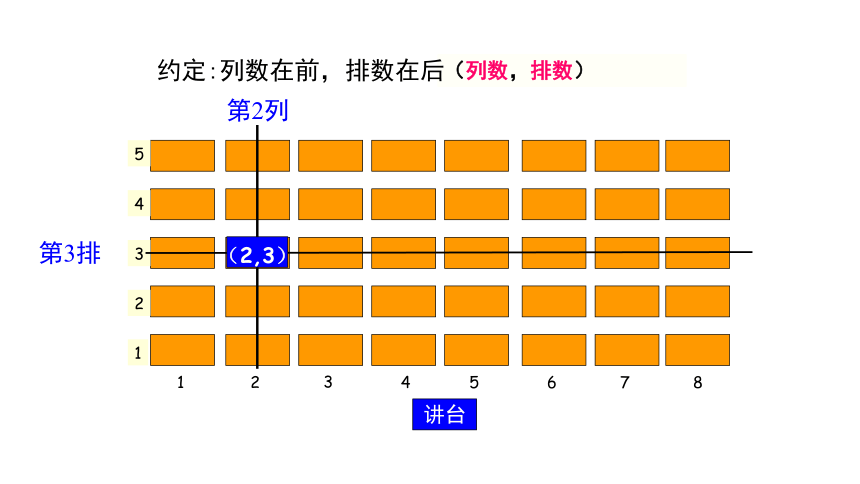
思考1 在班里老师想找一个学生,你知道是谁吗?
思考2 你认为确定一个位置需要几个数据?
提示1:只给一个数据“第2列”,你能确定老师要找的学生是谁吗?
提示2:给出两个数据“第2列,第3排”,你能确定是谁了吗?
平面直角坐标系
(1)在电影票上“6排3号”与“3排6号”中的“6”的含义有什么不同?你能找到它们对应的位置吗?
(2)如果将“6排3号”简记作(6,3),那么“3排6号”如何表示?(5,6)表示什么含义? (6,5)呢?
(3) 在只有一层的电影院内,确定一个座位一般需要几个数据?
答:两个数据:排数和号数.
做一做
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第3排
第2列
(2,3)
(列数,排数)
约定:列数在前,排数在后
平面直角坐标系:在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴,这就建立了平面直角坐标系.
如图,通常把其中水平的数轴叫做
x轴或横轴,取向右为正方向;
铅直的数轴叫做y轴或纵轴,取向
上为正方向;
两条数轴的交点O叫做坐标原点.
建立平面直角坐标系时,一定要注
明原点O、x轴和y轴,一般x,y标在箭头旁边
注意:x轴和y轴的单位长度可以相同,也可以不同(一般是一致的),其单位长度是根据需要而规定的.
2.x轴和y轴把平面分成四个象限,如图所示.
3.易错警示:象限以坐标轴为界,
x轴、y轴上的点不属于任何象限.
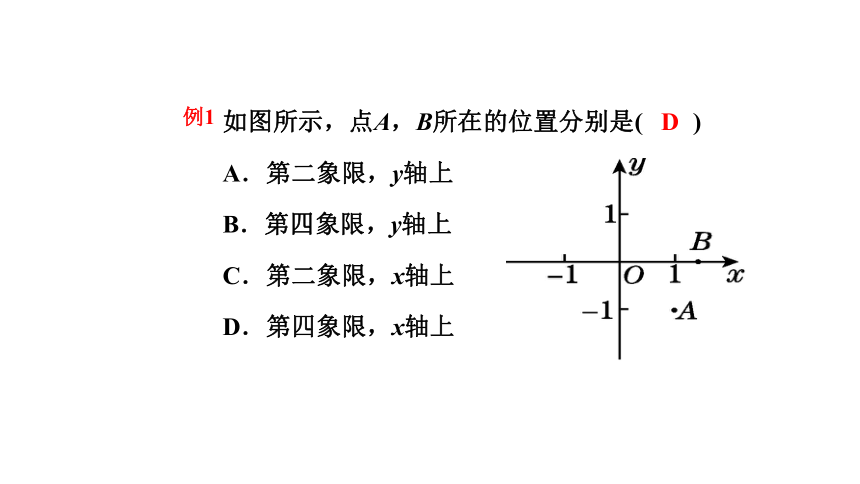
如图所示,点A,B所在的位置分别是( )
A.第二象限,y轴上
B.第四象限,y轴上
C.第二象限,x轴上
D.第四象限,x轴上
例1
D
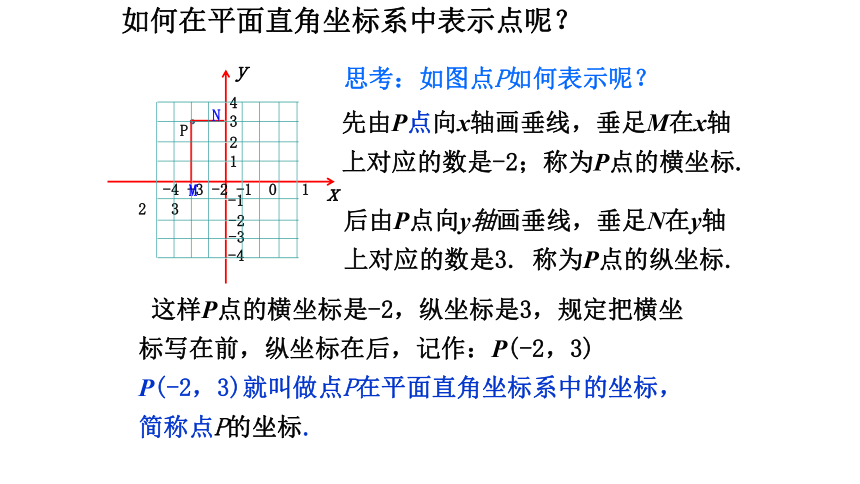
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上对应的数是3. 称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上对应的数是-2;称为P点的横坐标.
P
N
M
如何在平面直角坐标系中表示点呢?
2. 点的坐标:在平面直角坐标系中,任意一点都可以用一对有序实数来表示,对于平面直角坐标系中的任意一点A,过点A分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别称为点A的横坐标和纵坐标,可记作A(a,b).坐标平面中每一个点都可以用有序实数对表示,所以平面直角坐标系中的点和有序实数对是一一对应的关系.
要点精析:
平面直角坐标系中点的坐标是指一对有序实数,其顺序是先横后纵,所以在记一个点的坐标时,一定要横坐标在前,纵坐标在后,中间用逗号隔开,其位置不能颠倒.例如:(2,3)和(3,2)是完全不同的两个点的坐标.
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
0
A
(4,3)
x
y
1. 找出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
试一试
A
B
C
E
F
D
写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
2. 在平面直角坐标系中找点A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
各象限内、坐标轴上点的坐标特征
活动1: 观察坐标系,填写各象限内的点的坐标的特征:
点的位置
横标的符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,-1), D(2.5,-2), E(0,-4)所在的象限吗?你的方法又是什么?
点的位置
横坐标的符号
纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说出(-5,0),(0,-5),(3,0),
(0,3),(0,0)所在的位置吗?你的方法又是什么?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2.观察坐标系,填写坐标轴上的点的坐标的特征:
(1)各象限内点的坐标特征:设P(x,y),
若点P在第一象限,则x>0,y>0;
若点P在第二象限,则__________;
若点P在第三象限,则_________;
若点P在第四象限,则__________.
(2)坐标轴上点的坐标特征:
①若点P(x,y)在x轴上,则它的纵坐标____,横坐标x________
②若点P(x,y)在y轴上,则它的横坐标____,纵坐标y_________
③坐标原点是x轴和y轴的交点,它的横纵坐标_____,即x=y=0.
x<0,y>0
x<0,y<0
x>0,y<0
y=0
x=0
为任意实数
为任意实数
都为0
已知平面直角坐标系中有一点P(a+2,b-3).
(1)若点P在x轴上,则b=___;若点P在y轴上,则a=____.
(2)若点P在原点,则a=________,b=________;
(3)若b=2a,且点P在第三象限,求a的取值范围.
例3
3
-2
-2
3
x
y
O
如图,在平面直角坐标系中你能画出点A关于x轴的对称点吗?
A (2,3)
A′(2,-3)
你能说出点A与点A'坐标的关系吗?
特殊点的坐标的特征
x
y
O
在平面直角坐标系中画出下列各点关于x轴的对称点.
C (3,-4)
C '(3,4)
B(-4,2)
B '(-4,-2)
(x , y)
关于 x 轴
对称
( , )
x
-y
知识归纳
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(简称:横轴横相等)
P(x,y)关于x轴对称的点的坐标为P1(x,-y);
如图,在平面直角坐标系中你能画出点A关于y轴的对称点吗?
x
y
O
A (2,3)
A′(-2,3)
你能说出点A与点A'坐标的关系吗?
x
y
O
在平面直角坐标系中画出下列各点关于y轴的对称点.
C (3,-4)
C '(-3,-4)
B(-4,2)
B '(4,2)
(x , y)
关于 y轴
对称
( , )
-x
y
知识归纳
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
(简称:纵轴纵相等)
P(x,y)关于y轴对称的点的坐标为P2(-x,y);
如图,分别写出以下各点关于原点对称的点的坐标.
-4 -3 -2 -1O 1 2 3 4 5 x
y
4321
-1
-2
-3
-4
E
B
A
D
C
H
F
G
M
N
Q
思考:关于原点对称的两点的坐标又有何特征呢?
P
A(3,1),
B(1,3),
P(0,3),
C(-1,3),
D(-3,1)
M(0,3)
E(-3,-1),
F(-1,-3),
Q(0,-3),
G(1,-3),
H(3,-1)
N(0,-3)
O
x
y
(x,y)
M
N
(-x,-y)
总结归纳
关于原点对称的两点,横坐标和纵坐标都互为相反数.
(1)各象限角平分线上点的坐标特征:
若P(x,y)在第一、三象限的角平分线上,则x=y;
若P(x,y)在第二、四象限的角平分线上,则x=-y.
(2)对称点的坐标特征:
①关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
如P(x,y)关于x轴对称的点的坐标为P1(x,-y);
②关于y轴对称的两点,纵坐标相同,横坐标互为相反数,
如P(x,y)关于y轴对称的点的坐标为P2(-x,y);
归纳总结
③关于原点对称的两点,横、纵坐标分别互为相反数,如P(x,y)关于原点对称的点的坐标为P3(-x,-y).
(3)与x轴、y轴平行的直线上的点的坐标特征:过点(a, b)且与x轴平行的直线上的点的纵坐标y是不变的量,即y=b;
过点(a,b)且与y轴平行的直线上的点的横坐标x是不变的量,即x=a.
(4)点P(a,b)到x轴的距离为|b|,到y轴的距离为|a|.
根据“关于原点对称的点的横、纵坐标都互为相反数”可得点(-2,3)关于原点的对称点,再向左平移2个单位长度,只需“横坐标减2,纵坐标不变”可得答案.点(-2,3)关于原点的对称点是(2,-3),再向左平移2个单位长度得到的点的坐标是(0,-3).
导引:
在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
A.(4,-3) B.(-4,3)
C.(0,-3) D.(0,3)
例4
C
1.平面直角坐标系的三要素:
(1)两条数轴;(2)互相垂直;(3)公共原点.
2. 平面直角坐标系中两条数轴的特征:
(1)互相垂直; (2)原点重合;
(3)通常取向上、向右为正方向;
(4)单位长度一般取相同的.在有些实际问题中,两条数轴上的单位长度可以不同.
3. 坐标轴上的点不属于任何象限;坐标平面内的任何一个点,不在四个象限内就在坐标轴上.
(1)各象限内点的坐标特征:设P(x,y),
若点P在第一象限,则x>0,y>0;若点P在第二象限,则__________
若点P在第三象限,则_________;若点P在第四象限,则_________.
(2)坐标轴上点的坐标特征:
①若点P(x,y)在x轴上,则它的纵坐标____,横坐标x________
②若点P(x,y)在y轴上,则它的横坐标____,纵坐标y_________
③坐标原点是x轴和y轴的交点,它的横纵坐标_____,即x=y=0.
x<0,y>0
x<0,y<0
x>0,y<0
y=0
x=0
为任意实数
为任意实数
都为0
4、各象限内、坐标轴上点的坐标特征
(1)各象限角平分线上点的坐标特征:
若P(x,y)在第一、三象限的角平分线上,则x=y;
若P(x,y)在第二、四象限的角平分线上,则x=-y.
(2)对称点的坐标特征:
①关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
如P(x,y)关于x轴对称的点的坐标为P1(x,-y);
②关于y轴对称的两点,纵坐标相同,横坐标互为相反数,
如P(x,y)关于y轴对称的点的坐标为P2(-x,y);
5、特殊点的坐标的特征
③关于原点对称的两点,横、纵坐标分别互为相反数,如P(x,y)关于原点对称的点的坐标为P3(-x,-y).
(3)与x轴、y轴平行的直线上的点的坐标特征:过点(a, b)且与x轴平行的直线上的点的纵坐标y是不变的量,即y=b;
过点(a,b)且与y轴平行的直线上的点的横坐标x是不变的量,即x=a.
(4)点P(a,b)到x轴的距离为|b|,到y轴的距离为|a|.
17.2 函数的图象
第1课时 平面直角坐标系
复习引入
在数轴上,如何确定一个点的位置呢?
A点记作-2,B点记作3.也就是说,
例如:
在数轴上一般用一个数据就可以表示一个点的位置.
小明父子俩周末去电影院看国产大片《战狼2》,买了两张票去观看,座位号分别是3排6座和6排3座.怎样才能既快又准地找到座位?
情境引入
思考1 在班里老师想找一个学生,你知道是谁吗?
思考2 你认为确定一个位置需要几个数据?
提示1:只给一个数据“第2列”,你能确定老师要找的学生是谁吗?
提示2:给出两个数据“第2列,第3排”,你能确定是谁了吗?
平面直角坐标系
(1)在电影票上“6排3号”与“3排6号”中的“6”的含义有什么不同?你能找到它们对应的位置吗?
(2)如果将“6排3号”简记作(6,3),那么“3排6号”如何表示?(5,6)表示什么含义? (6,5)呢?
(3) 在只有一层的电影院内,确定一个座位一般需要几个数据?
答:两个数据:排数和号数.
做一做
讲台
2
1
3
4
5
6
7
8
1
2
3
4
5
第3排
第2列
(2,3)
(列数,排数)
约定:列数在前,排数在后
平面直角坐标系:在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴,这就建立了平面直角坐标系.
如图,通常把其中水平的数轴叫做
x轴或横轴,取向右为正方向;
铅直的数轴叫做y轴或纵轴,取向
上为正方向;
两条数轴的交点O叫做坐标原点.
建立平面直角坐标系时,一定要注
明原点O、x轴和y轴,一般x,y标在箭头旁边
注意:x轴和y轴的单位长度可以相同,也可以不同(一般是一致的),其单位长度是根据需要而规定的.
2.x轴和y轴把平面分成四个象限,如图所示.
3.易错警示:象限以坐标轴为界,
x轴、y轴上的点不属于任何象限.
如图所示,点A,B所在的位置分别是( )
A.第二象限,y轴上
B.第四象限,y轴上
C.第二象限,x轴上
D.第四象限,x轴上
例1
D
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3)
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
后由P点向y轴画垂线,垂足N在y轴上对应的数是3. 称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上对应的数是-2;称为P点的横坐标.
P
N
M
如何在平面直角坐标系中表示点呢?
2. 点的坐标:在平面直角坐标系中,任意一点都可以用一对有序实数来表示,对于平面直角坐标系中的任意一点A,过点A分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别称为点A的横坐标和纵坐标,可记作A(a,b).坐标平面中每一个点都可以用有序实数对表示,所以平面直角坐标系中的点和有序实数对是一一对应的关系.
要点精析:
平面直角坐标系中点的坐标是指一对有序实数,其顺序是先横后纵,所以在记一个点的坐标时,一定要横坐标在前,纵坐标在后,中间用逗号隔开,其位置不能颠倒.例如:(2,3)和(3,2)是完全不同的两个点的坐标.
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
0
A
(4,3)
x
y
1. 找出点A的坐标.
(1)过点A作x轴的垂线,垂足在x轴上对应的数是4;
(2)过点A作y轴的垂线,垂足在y轴上对应的数是3;
点A的坐标为(4,3)
试一试
A
B
C
E
F
D
写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
2. 在平面直角坐标系中找点A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
各象限内、坐标轴上点的坐标特征
活动1: 观察坐标系,填写各象限内的点的坐标的特征:
点的位置
横标的符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,-1), D(2.5,-2), E(0,-4)所在的象限吗?你的方法又是什么?
点的位置
横坐标的符号
纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说出(-5,0),(0,-5),(3,0),
(0,3),(0,0)所在的位置吗?你的方法又是什么?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2.观察坐标系,填写坐标轴上的点的坐标的特征:
(1)各象限内点的坐标特征:设P(x,y),
若点P在第一象限,则x>0,y>0;
若点P在第二象限,则__________;
若点P在第三象限,则_________;
若点P在第四象限,则__________.
(2)坐标轴上点的坐标特征:
①若点P(x,y)在x轴上,则它的纵坐标____,横坐标x________
②若点P(x,y)在y轴上,则它的横坐标____,纵坐标y_________
③坐标原点是x轴和y轴的交点,它的横纵坐标_____,即x=y=0.
x<0,y>0
x<0,y<0
x>0,y<0
y=0
x=0
为任意实数
为任意实数
都为0
已知平面直角坐标系中有一点P(a+2,b-3).
(1)若点P在x轴上,则b=___;若点P在y轴上,则a=____.
(2)若点P在原点,则a=________,b=________;
(3)若b=2a,且点P在第三象限,求a的取值范围.
例3
3
-2
-2
3
x
y
O
如图,在平面直角坐标系中你能画出点A关于x轴的对称点吗?
A (2,3)
A′(2,-3)
你能说出点A与点A'坐标的关系吗?
特殊点的坐标的特征
x
y
O
在平面直角坐标系中画出下列各点关于x轴的对称点.
C (3,-4)
C '(3,4)
B(-4,2)
B '(-4,-2)
(x , y)
关于 x 轴
对称
( , )
x
-y
知识归纳
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(简称:横轴横相等)
P(x,y)关于x轴对称的点的坐标为P1(x,-y);
如图,在平面直角坐标系中你能画出点A关于y轴的对称点吗?
x
y
O
A (2,3)
A′(-2,3)
你能说出点A与点A'坐标的关系吗?
x
y
O
在平面直角坐标系中画出下列各点关于y轴的对称点.
C (3,-4)
C '(-3,-4)
B(-4,2)
B '(4,2)
(x , y)
关于 y轴
对称
( , )
-x
y
知识归纳
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
(简称:纵轴纵相等)
P(x,y)关于y轴对称的点的坐标为P2(-x,y);
如图,分别写出以下各点关于原点对称的点的坐标.
-4 -3 -2 -1O 1 2 3 4 5 x
y
4321
-1
-2
-3
-4
E
B
A
D
C
H
F
G
M
N
Q
思考:关于原点对称的两点的坐标又有何特征呢?
P
A(3,1),
B(1,3),
P(0,3),
C(-1,3),
D(-3,1)
M(0,3)
E(-3,-1),
F(-1,-3),
Q(0,-3),
G(1,-3),
H(3,-1)
N(0,-3)
O
x
y
(x,y)
M
N
(-x,-y)
总结归纳
关于原点对称的两点,横坐标和纵坐标都互为相反数.
(1)各象限角平分线上点的坐标特征:
若P(x,y)在第一、三象限的角平分线上,则x=y;
若P(x,y)在第二、四象限的角平分线上,则x=-y.
(2)对称点的坐标特征:
①关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
如P(x,y)关于x轴对称的点的坐标为P1(x,-y);
②关于y轴对称的两点,纵坐标相同,横坐标互为相反数,
如P(x,y)关于y轴对称的点的坐标为P2(-x,y);
归纳总结
③关于原点对称的两点,横、纵坐标分别互为相反数,如P(x,y)关于原点对称的点的坐标为P3(-x,-y).
(3)与x轴、y轴平行的直线上的点的坐标特征:过点(a, b)且与x轴平行的直线上的点的纵坐标y是不变的量,即y=b;
过点(a,b)且与y轴平行的直线上的点的横坐标x是不变的量,即x=a.
(4)点P(a,b)到x轴的距离为|b|,到y轴的距离为|a|.
根据“关于原点对称的点的横、纵坐标都互为相反数”可得点(-2,3)关于原点的对称点,再向左平移2个单位长度,只需“横坐标减2,纵坐标不变”可得答案.点(-2,3)关于原点的对称点是(2,-3),再向左平移2个单位长度得到的点的坐标是(0,-3).
导引:
在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
A.(4,-3) B.(-4,3)
C.(0,-3) D.(0,3)
例4
C
1.平面直角坐标系的三要素:
(1)两条数轴;(2)互相垂直;(3)公共原点.
2. 平面直角坐标系中两条数轴的特征:
(1)互相垂直; (2)原点重合;
(3)通常取向上、向右为正方向;
(4)单位长度一般取相同的.在有些实际问题中,两条数轴上的单位长度可以不同.
3. 坐标轴上的点不属于任何象限;坐标平面内的任何一个点,不在四个象限内就在坐标轴上.
(1)各象限内点的坐标特征:设P(x,y),
若点P在第一象限,则x>0,y>0;若点P在第二象限,则__________
若点P在第三象限,则_________;若点P在第四象限,则_________.
(2)坐标轴上点的坐标特征:
①若点P(x,y)在x轴上,则它的纵坐标____,横坐标x________
②若点P(x,y)在y轴上,则它的横坐标____,纵坐标y_________
③坐标原点是x轴和y轴的交点,它的横纵坐标_____,即x=y=0.
x<0,y>0
x<0,y<0
x>0,y<0
y=0
x=0
为任意实数
为任意实数
都为0
4、各象限内、坐标轴上点的坐标特征
(1)各象限角平分线上点的坐标特征:
若P(x,y)在第一、三象限的角平分线上,则x=y;
若P(x,y)在第二、四象限的角平分线上,则x=-y.
(2)对称点的坐标特征:
①关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
如P(x,y)关于x轴对称的点的坐标为P1(x,-y);
②关于y轴对称的两点,纵坐标相同,横坐标互为相反数,
如P(x,y)关于y轴对称的点的坐标为P2(-x,y);
5、特殊点的坐标的特征
③关于原点对称的两点,横、纵坐标分别互为相反数,如P(x,y)关于原点对称的点的坐标为P3(-x,-y).
(3)与x轴、y轴平行的直线上的点的坐标特征:过点(a, b)且与x轴平行的直线上的点的纵坐标y是不变的量,即y=b;
过点(a,b)且与y轴平行的直线上的点的横坐标x是不变的量,即x=a.
(4)点P(a,b)到x轴的距离为|b|,到y轴的距离为|a|.
