华师大版八年级下册17.2.2 函数的图象课件(23张ppt)
文档属性
| 名称 | 华师大版八年级下册17.2.2 函数的图象课件(23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 13:27:14 | ||
图片预览






文档简介
第17章 函数及其图象
17.2 函数的图象
第2课时 函数的图象
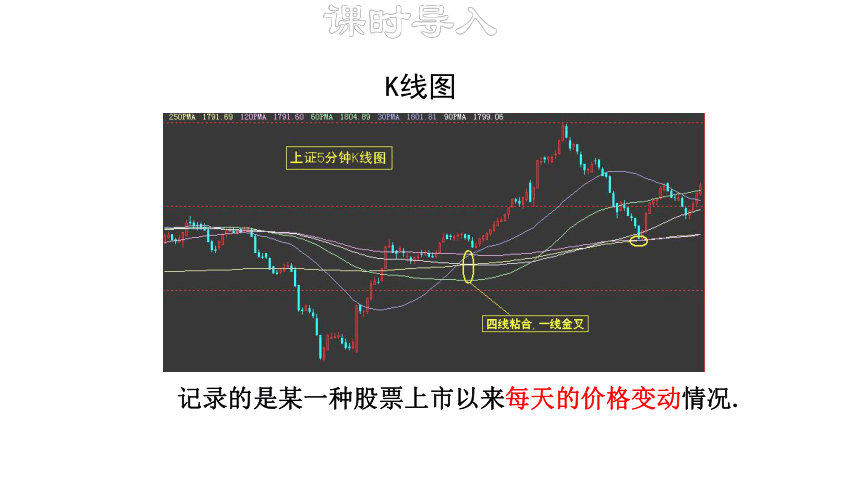
记录的是某一种股票上市以来每天的价格变动情况.
K线图
心电图
记录的是心脏本身的生物电在每一心动周期中发生的电变化情况.
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T(?C)
2
4
6
8
-2
0
回顾和思考
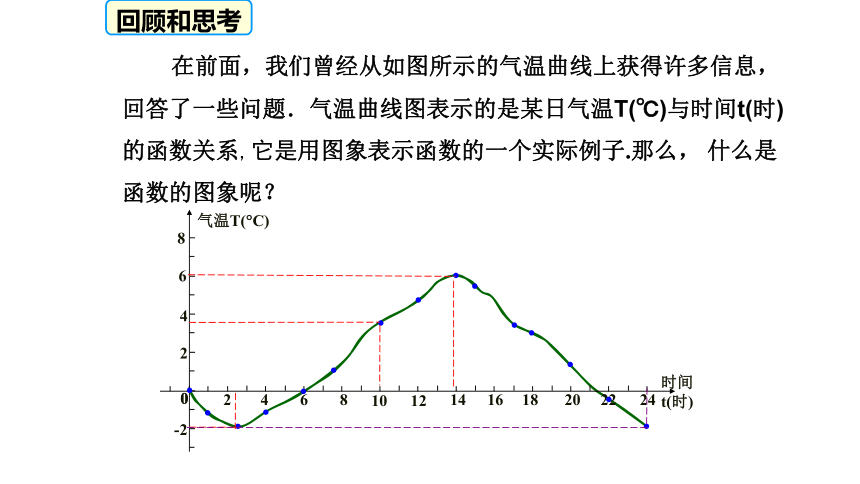
在前面,我们曾经从如图所示的气温曲线上获得许多信息,回答了一些问题.气温曲线图表示的是某日气温T(℃)与时间t(时)的函数关系,它是用图象表示函数的一个实际例子.那么, 什么是函数的图象呢?
函数的图象
定义:一般来说,函数的图象是由平面直角坐标系中一系列的点组成的,图象上每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与该自变量的值对应的函数值.
(2)怎样获得组成图形的点?
先确定点的坐标
(4)自变量x 的一个确定的值与它所对应的唯一的函数值y,是否唯一确定了一个点(x,y)呢?
取一些自变量的值,计算出相应的函数值.
(3)怎样确定满足函数关系的点的坐标?
(1)在平面直角坐标系中,平面内的点可以用一对_______ 来表示.即坐标平面内 与有序数对是一一 的.
有序数对
点
对应
想一想:
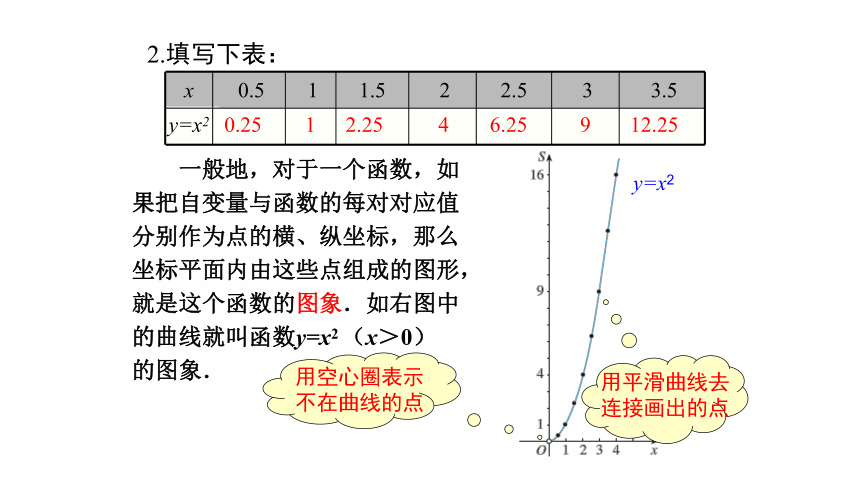
2.填写下表:
x
0.5
1
1.5
2
2.5
3
3.5
y=x2
0.25
1
2.25
4
6.25
9
12.25
一般地,对于一个函数,如
果把自变量与函数的每对对应值
分别作为点的横、纵坐标,那么
坐标平面内由这些点组成的图形,
就是这个函数的图象.如右图中
的曲线就叫函数y=x2 (x>0)
的图象.
用空心圈表示不在曲线的点
用平滑曲线去连接画出的点
y=x2
要点精析:
(1)函数图象上的任意点P(x,y)中的x,y都满足函数关系,另一方面,满足函数关系的任意一对有序实数对(x,y)所对应的点一定在函数的图象上.
(2)函数图象上的所有点与函数关系式中的两个变量的关系是一一对应的.它们是函数中的两个变量间的关系的两种不同(一个是“数”,一个是“形”)的呈现方式.
已知函数y=2x-1.
(1)试判断点A(-1,3)和点B 是否在此函数的图象上;
(2)已知点C(a,a+1)在此函数的图象上,求a的值.
例1
(1)∵当x=-1时,y=2×(-1)-1=-3≠3,
∴点A不在函数y=2x-1的图象上.
∵当x= 时,y=2× -1=- , ∴点B在函数y=2x-1的图象上
(2)∵点C(a,a+1)在函数y=2x-1的图象上,
∴把x=a,y=a+1代入y=2x-1,得a+1=2a-1. 解得a=2.
解:
画出下列函数的图象:
(1) ; (2) .
解:(1)从函数解析式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值, 算出y的
对应值,填写在表格里:
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
-5 -3 -1 1 3 5 7
全体实数
用描点法画函数的图象
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
当自变量的值越来越大时,
对应的函数值 .
画出的图象是一条 ,
直线
越来越大
-6
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
为什么没有“0”?
解:(2)列表 :取一些自变量的值,并求出对应的函数值,填入表中.
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
(2)描点: 分别以表中
对应的x、y为横纵
坐标,在坐标系中描
出对应的点.
(3)连线: 用光滑的曲线把这些点依次连接起来.
(1,-6)
第一步,列表——表中给出一些自变量的值(注意自变量的取值范围)及其 ;
第二步,描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,描出表格中各数对对应的各点;
第三步:连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
归纳总结
画函数图象的一般步骤:
画出下列函数的图象:
y=2x,
{2D5ABB26-0587-4C30-8999-92F81FD0307C}
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
解:(1)函数y=2x中自变量x可为任意实数.
①列表如下:
练一练
y=2x
②描点;
③连线.
同样可以画出函数 的图象.
画出函数 的图象.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-3
-2
-1
0
1
2
3
…
y
…
…
4.5
2
0.5
0.5
2
4.5
0
·
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
·
·
·
·
·
王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:
实际问题中的函数图象
解:由图象可知:(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米;
(2)山顶离山脚的距离是300米,小强先爬上山;
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
O
(3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷;
(3)小强需多少时间追上爷爷?
O
小强爬山300米用了10分钟,速度为30米/分,爷爷爬山(300-60)米=240米,用了10.5分钟,速度约为23米/分,因此小强的速度大,大7米/分.
O
(4)谁的速度大?大多少?
由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相
应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用
光滑的曲线连结起来.
17.2 函数的图象
第2课时 函数的图象
记录的是某一种股票上市以来每天的价格变动情况.
K线图
心电图
记录的是心脏本身的生物电在每一心动周期中发生的电变化情况.
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T(?C)
2
4
6
8
-2
0
回顾和思考
在前面,我们曾经从如图所示的气温曲线上获得许多信息,回答了一些问题.气温曲线图表示的是某日气温T(℃)与时间t(时)的函数关系,它是用图象表示函数的一个实际例子.那么, 什么是函数的图象呢?
函数的图象
定义:一般来说,函数的图象是由平面直角坐标系中一系列的点组成的,图象上每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与该自变量的值对应的函数值.
(2)怎样获得组成图形的点?
先确定点的坐标
(4)自变量x 的一个确定的值与它所对应的唯一的函数值y,是否唯一确定了一个点(x,y)呢?
取一些自变量的值,计算出相应的函数值.
(3)怎样确定满足函数关系的点的坐标?
(1)在平面直角坐标系中,平面内的点可以用一对_______ 来表示.即坐标平面内 与有序数对是一一 的.
有序数对
点
对应
想一想:
2.填写下表:
x
0.5
1
1.5
2
2.5
3
3.5
y=x2
0.25
1
2.25
4
6.25
9
12.25
一般地,对于一个函数,如
果把自变量与函数的每对对应值
分别作为点的横、纵坐标,那么
坐标平面内由这些点组成的图形,
就是这个函数的图象.如右图中
的曲线就叫函数y=x2 (x>0)
的图象.
用空心圈表示不在曲线的点
用平滑曲线去连接画出的点
y=x2
要点精析:
(1)函数图象上的任意点P(x,y)中的x,y都满足函数关系,另一方面,满足函数关系的任意一对有序实数对(x,y)所对应的点一定在函数的图象上.
(2)函数图象上的所有点与函数关系式中的两个变量的关系是一一对应的.它们是函数中的两个变量间的关系的两种不同(一个是“数”,一个是“形”)的呈现方式.
已知函数y=2x-1.
(1)试判断点A(-1,3)和点B 是否在此函数的图象上;
(2)已知点C(a,a+1)在此函数的图象上,求a的值.
例1
(1)∵当x=-1时,y=2×(-1)-1=-3≠3,
∴点A不在函数y=2x-1的图象上.
∵当x= 时,y=2× -1=- , ∴点B在函数y=2x-1的图象上
(2)∵点C(a,a+1)在函数y=2x-1的图象上,
∴把x=a,y=a+1代入y=2x-1,得a+1=2a-1. 解得a=2.
解:
画出下列函数的图象:
(1) ; (2) .
解:(1)从函数解析式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值, 算出y的
对应值,填写在表格里:
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
-5 -3 -1 1 3 5 7
全体实数
用描点法画函数的图象
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
当自变量的值越来越大时,
对应的函数值 .
画出的图象是一条 ,
直线
越来越大
-6
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
为什么没有“0”?
解:(2)列表 :取一些自变量的值,并求出对应的函数值,填入表中.
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
(2)描点: 分别以表中
对应的x、y为横纵
坐标,在坐标系中描
出对应的点.
(3)连线: 用光滑的曲线把这些点依次连接起来.
(1,-6)
第一步,列表——表中给出一些自变量的值(注意自变量的取值范围)及其 ;
第二步,描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,描出表格中各数对对应的各点;
第三步:连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
归纳总结
画函数图象的一般步骤:
画出下列函数的图象:
y=2x,
{2D5ABB26-0587-4C30-8999-92F81FD0307C}
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
解:(1)函数y=2x中自变量x可为任意实数.
①列表如下:
练一练
y=2x
②描点;
③连线.
同样可以画出函数 的图象.
画出函数 的图象.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-3
-2
-1
0
1
2
3
…
y
…
…
4.5
2
0.5
0.5
2
4.5
0
·
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
·
·
·
·
·
王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:
实际问题中的函数图象
解:由图象可知:(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米;
(2)山顶离山脚的距离是300米,小强先爬上山;
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
O
(3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷;
(3)小强需多少时间追上爷爷?
O
小强爬山300米用了10分钟,速度为30米/分,爷爷爬山(300-60)米=240米,用了10.5分钟,速度约为23米/分,因此小强的速度大,大7米/分.
O
(4)谁的速度大?大多少?
由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相
应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用
光滑的曲线连结起来.
