江西省井冈山实验学校2011-2012学年高二下学期第一次月考数学(文)试题(无答案)
文档属性
| 名称 | 江西省井冈山实验学校2011-2012学年高二下学期第一次月考数学(文)试题(无答案) | 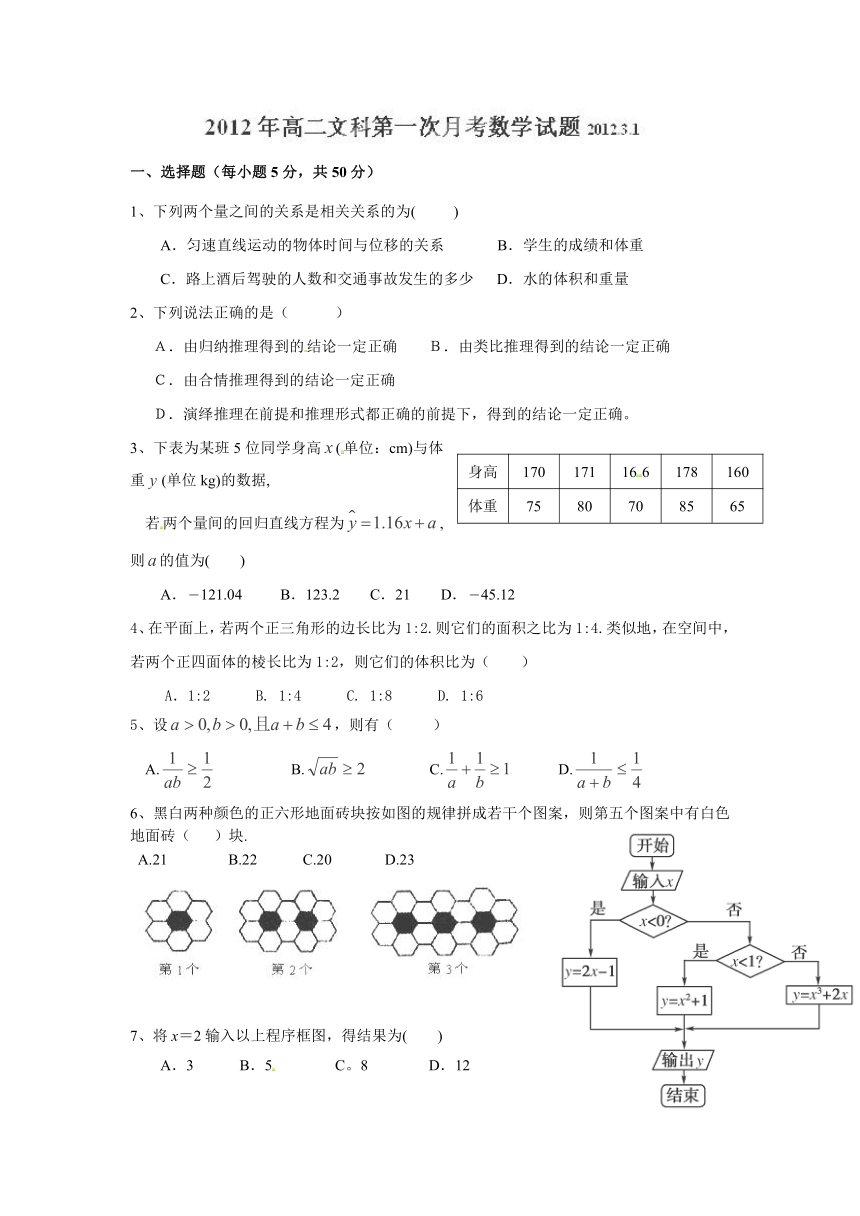 | |
| 格式 | zip | ||
| 文件大小 | 157.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-12 16:53:54 | ||
图片预览



文档简介
一、选择题(每小题5分,共50分)
1、下列两个量之间的关系是相关关系的为( )
A.匀速直线运动的物体时间与位移的关系 B.学生的成绩和体重
C.路上酒后驾驶的人数和交通事故发生的多少 D.水的体积和重量
2、下列说法正确的是( )
A.由归纳推理得到的结论一定正确 B.由类比推理得到的结论一定正确
C.由合情推理得到的结论一定正确
D.演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确。
身高 170 171 166 178 160
体重 75 80 70 85 65
3、下表为某班5位同学身高(单位:cm)与体重(单位kg)的数据,
若两个量间的回归直线方程为,则的值为( )
A.121.04 B.123.2 C.21 D.45.12
4、在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
A.1:2 B. 1:4 C. 1:8 D. 1:6
5、设,则有( )
A. B. C. D.
6、黑白两种颜色的正六形地面砖块按如图的规律拼成若干个图案,则第五个图案中有白色地面砖( )块.
A.21 B.22 C.20 D.23
7、将x=2输入以上程序框图,得结果为( )
A.3 B.5 C。8 D.12
8、在10个球中有6个红球和4个白球,不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为( )
A. B. C. D.
9、一袋中有3个红球,2个白球,另一袋中有2个红球,1个白球,从每袋中任取一球,则至少取到1个白球的概率是( )
A. B. C. D.
10、有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖”。四位歌手的话只有两名是对的,则获奖的歌手是( )
A.甲 B.乙 C.丙 D.丁
二、填空题(每小题5分,共25分)
11、回归直线方程为,则时,的估计值为
12.已知一列数1,-5,9,-13,17,……,根据其规律,下一个数应为
13、在平面几何里,有勾股定理:“设的两边AB、AC互相垂直,则。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
14、若且,则
15、将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
. . . . . . .
按照以上排列的规律,第 行()从左向右的第3个数为 .
高二文科第一次月考数学试题
班级 考号 姓名 得分
一、选择题(每小题5分共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(本大题共5小题,每小题5分,共25分. 把答案填在对应题号后的横线上)
11、 12、 13、
14、 15、
三、解答题(共6小题,共75分)
16、在数列{an}中,,试写出这个数列的前4项,并猜想这个数列的通项公式。
17、求证:
18、某招聘会正如火如荼进行着,甲、乙、丙三名大学生跃跃欲试,已知甲能被录用的概率为,甲、乙两人都不能被录用的概率为,乙、丙两人都能被录用的概率为.
(Ⅰ)乙、丙两人各自能被录用的概率;
(Ⅱ)求甲、乙、丙三人至少有一人能被录用的概率.
19、在中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,
a、b、c成等比数列,求证:为等边三角形。
20、如图,是正方形,是正方形的中心,
底面,是的中点.
求证:(1)//平面;
(2)平面平面.
21、函数 f (x) 对任意x R都有.
(1)求的值.
(2)数列{an} 满足:,数列是等差数列吗 请给予证明.
1、下列两个量之间的关系是相关关系的为( )
A.匀速直线运动的物体时间与位移的关系 B.学生的成绩和体重
C.路上酒后驾驶的人数和交通事故发生的多少 D.水的体积和重量
2、下列说法正确的是( )
A.由归纳推理得到的结论一定正确 B.由类比推理得到的结论一定正确
C.由合情推理得到的结论一定正确
D.演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确。
身高 170 171 166 178 160
体重 75 80 70 85 65
3、下表为某班5位同学身高(单位:cm)与体重(单位kg)的数据,
若两个量间的回归直线方程为,则的值为( )
A.121.04 B.123.2 C.21 D.45.12
4、在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
A.1:2 B. 1:4 C. 1:8 D. 1:6
5、设,则有( )
A. B. C. D.
6、黑白两种颜色的正六形地面砖块按如图的规律拼成若干个图案,则第五个图案中有白色地面砖( )块.
A.21 B.22 C.20 D.23
7、将x=2输入以上程序框图,得结果为( )
A.3 B.5 C。8 D.12
8、在10个球中有6个红球和4个白球,不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为( )
A. B. C. D.
9、一袋中有3个红球,2个白球,另一袋中有2个红球,1个白球,从每袋中任取一球,则至少取到1个白球的概率是( )
A. B. C. D.
10、有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖”。四位歌手的话只有两名是对的,则获奖的歌手是( )
A.甲 B.乙 C.丙 D.丁
二、填空题(每小题5分,共25分)
11、回归直线方程为,则时,的估计值为
12.已知一列数1,-5,9,-13,17,……,根据其规律,下一个数应为
13、在平面几何里,有勾股定理:“设的两边AB、AC互相垂直,则。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
14、若且,则
15、将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
. . . . . . .
按照以上排列的规律,第 行()从左向右的第3个数为 .
高二文科第一次月考数学试题
班级 考号 姓名 得分
一、选择题(每小题5分共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(本大题共5小题,每小题5分,共25分. 把答案填在对应题号后的横线上)
11、 12、 13、
14、 15、
三、解答题(共6小题,共75分)
16、在数列{an}中,,试写出这个数列的前4项,并猜想这个数列的通项公式。
17、求证:
18、某招聘会正如火如荼进行着,甲、乙、丙三名大学生跃跃欲试,已知甲能被录用的概率为,甲、乙两人都不能被录用的概率为,乙、丙两人都能被录用的概率为.
(Ⅰ)乙、丙两人各自能被录用的概率;
(Ⅱ)求甲、乙、丙三人至少有一人能被录用的概率.
19、在中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,
a、b、c成等比数列,求证:为等边三角形。
20、如图,是正方形,是正方形的中心,
底面,是的中点.
求证:(1)//平面;
(2)平面平面.
21、函数 f (x) 对任意x R都有.
(1)求的值.
(2)数列{an} 满足:,数列是等差数列吗 请给予证明.
同课章节目录
