9.4 正方形的性质和判定 同步训练(含解析)
文档属性
| 名称 | 9.4 正方形的性质和判定 同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 07:10:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学苏科版八年级下册9.4
正方形的性质和判定
同步训练
一、单选题(本题共10题,每题3分,共30分)
1.以下命题中正确的是(?
)
A.?对角线相等的平行四边形是正方形??????????????????????
B.?对角线互相垂直的平行四边形是正方形
C.?对角线相等且互相平分的四边形是正方形???????????D.?对角线相等且互相垂直平分的四边形是正方形
2.如图,正方形ABCD的面积为8,菱形AECF的面积为4,则EF的长是(???
)
A.?4??????????????????????????????????????????B.???????????????????????????????????????????C.?2??????????????????????????????????????????D.?1
3.边长分别为2和4的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为(??
)
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?12
4.如图,正方形
的边长为
,
,
,连接
,则线段
的长为(??
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
5.如图,在正方形ABCD中,BD=2,∠DCE是正方形ABCD的外角,P是∠DCE的角平分线CF上任意一点,则△PBD的面积等于( )
A.?1??????????????????????????????????????????B.?1.5??????????????????????????????????????????C.?2??????????????????????????????????????????D.?2.5
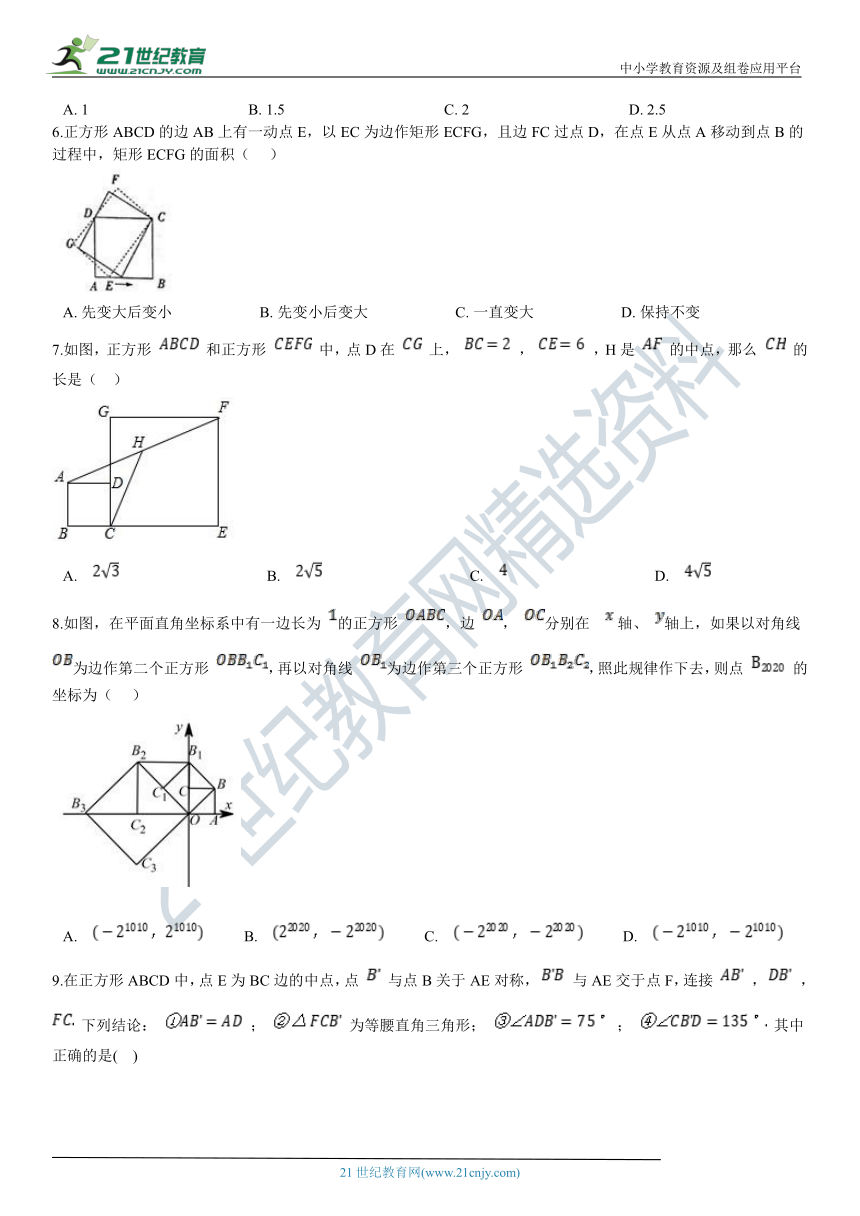
6.正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FC过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积(
???)
A.?先变大后变小???????????????????????B.?先变小后变大???????????????????????C.?一直变大???????????????????????D.?保持不变
7.如图,正方形
和正方形
中,点D在
上,
,
,H是
的中点,那么
的长是(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
8.如图,在平面直角坐标系中有一边长为
的正方形
,边
,
分别在
?轴、
轴上,如果以对角线
为边作第二个正方形
,再以对角线
为边作第三个正方形
,照此规律作下去,则点
的坐标为(???
)
A.???????????B.???????????C.???????????D.?
9.在正方形ABCD中,点E为BC边的中点,点
与点B关于AE对称,
与AE交于点F,连接
,
,
下列结论:
;
为等腰直角三角形;
;
其中正确的是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
10.如图,在正方形ABCD中,AC、BD相交于点O,E、F分别为BC、CD上的两点,BE=CF,AE、BF分别交BD、AC于M、N两点,连OE、OF.下列结论:①AE=BF;②AE⊥BF;③CE+CF=BD;④S四边形OECF=
S正方形ABCD
,
其中正确的是(
??????????)
A.?①②?????????????????????????????????B.?①④?????????????????????????????????C.?①②④?????????????????????????????????D.?①②③④
二、填空题(本题共8题,每题2分,共16分)
11.如图,正方形
的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且
,则四边形
的面积为________.
12.如图,两个正方形的边长分别为
、
,若
,
,则四边形
(阴影部分)的面积为________
13.如图,在正方形
中,直线
分别过
三点且
,若
与
的距离为
,
与
的距离为
,则正方形
的边长是________.
14.如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是________cm.
15.如图,在正方形ABCD中,P为对角线BD上一点,过P作PE⊥BC于E,PF⊥CD于F,若PE=1,PF=3,则AP=________?。
16.如图,矩形纸片
中,已知
,
,点
在
边上,沿
折叠纸片,使点
落在点
处,连结
,当
为直角三角形时,
的长为________.
17.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为2的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=4
EF,则正方形ABCD的面积为________
18.如图,边长为2的正方形ABCD中,AE平分∠DAC
,
AE交CD于点F
,
CE⊥AE
,
垂足为点E
,
EG⊥CD
,
垂足为点G
,
点H在边BC上,BH=DF
,
连接AH、FH
,
FH与AC交于点M
,
以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=
AF;⑤EG2=FG?DG
,
其中正确结论的有________(只填序号).
三、解答题(本题共7题,共84分)
19.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),
,且
.求证:四边形ABCD是正方形.
20.正方形ABCD和正方形CEFG的边长分别为b和a将它们如图所示放置,求图中阴影部分的面积.
21.如图,正方形ABCD的对角线AC,BD相交于点O.E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OG=OE.
22.如图,边长为2的正方形ABCD中,P是对角线AC上的一个动点(点P不与A、C重合),连结BP,过点B作
且使得
,连结QP交BC于点E,延长QP与直线AD交于点F.
(1)
面积的最小值为________;
(2)连结CQ,求证:
;
(3)猜想PF与EQ的数量关系,并说明理由.
23.如图(1),正方形
的对角线
相交于点
是
上一点,连接
过点A作
垂足为
与
相交于点F.
(1)直接写出
与
的数量关系;
(2)如图(2)若点E在
的延长线上,
于点
交
的延长线于点F,其他条件不变.试探究
与
的数量关系,并说明理由.
24.如图①,
的顶点P在正方形
两条对角线的交点处,
,将
绕点P旋转,旋转过程中
的两边分别与正方形
的边
和
交于点E和点F(点F与点C、D不重合).
(1)如图①,当
时,
、
、
之间满足的数量关系是________;
(2)如图②,将图①中的正方形
改为
的菱形,其他条件不变,当
时,(1)中的结论变为
,并给出证明过程;
(3)在(2)的条件下,若旋转过程中
的边
与边
的延长线交于点E,其他条件不变,探究在整个运动变化过程中,
、
、
之间满足的数量关系,直接写出结论,不用加以证明.
25.如图1,点E是正方形ABCD边AB上任意一点,以BE为边作正方形BEFG
,
连接DF
,
点M
,
N分别是线段AE、DF中点,连接MN
.
(1)请猜想MN与AE的关系,并证明你的结论;
(2)把图1中的正方形BEFG绕点B顺时针旋转
,此时点E、G恰好分别落在线段BC、AB上,如图2,其他条件不变,(1)中的结论是否成立?请说明理由.
答案解析部分
一、单选题
1.【答案】
D
解:A、对角线相等的平行四边形是矩形,故不符合题意;
B、对角线互相垂直的平行四边形是菱形,故不符合题意;
C、对角线相等且互相平分的四边形是矩形,故不符合题意;
D、对角线相等且互相垂直平分的四边形是正方形,符合题意,
故答案为:D.
2.【答案】
C
解:连接AC,如下图所示:
∵正方形ABCD的面积为8
∴AD=
∴在Rt△ACD中,由勾股定理知:
,
∵菱形AECF的面积为4,
∴
×EF×AC=4,代入AC=4,
故求得EF=2.
故答案选:C.
3.【答案】
B
解:如图,
∵BC=4,CE=2,
∴BE=2,
∴BE=
BC,
∵边长分别为2和4的两个正方形按如图的样式摆放并连线,
∴ER//CQ,
∴ER为△BCQ的中位线,
∴ER=
CQ=1,
∴S阴影=S△ABQ-S△BER=
AB·BC-
BE·ER=
×4×4-
×2×1=7,
故答案为:B.
4.【答案】
B
解:如图,延长
交
于点
,
,
,
,
,
和
是直角三角形,
在
和
中,
,
,
,
,
,
,
又
,
,
,
,
在
和
中,
,
,
,
,
,
,
同理可得
,
在
中,
,
故答案为:B.
5.【答案】
A
CG⊥BD于G,
∵CF是∠DCE的平分线,
∴∠FCE=45°,
∵∠DBC=45°,
∴CF∥BD,
∴CG等于△PBD的高,
∵BD=2,
∴CG=1,
△PBD的面积等于=1.
故答案为:A.
6.【答案】
D
解:连接DE,
∵S△CDE=S四边形CEGF,S△CDE=S正方形ABCD
,
∴S四边形CEGF=S正方形ABCD
,
故答案为:D.
7.【答案】
B
解:如图,连接AC、CF,
在正方形ABCD和正方形CEFG中,AC=
BC=2
,CF=
CE=6
,
∠ACD=∠GCF=45°,
所以,∠ACF=45°+45°=90°,
所以,△ACF是直角三角形,
由勾股定理得,AF=
=4
,
∵H是AF的中点,
∴CH=
AF=
×4
=2
.
故答案为:B.
8.【答案】
D
解:
∵正方形OABC边长为1,
∴OB=,
∴OB1=2,
∴B1点坐标为(0,2),
同理可知B2点坐标为(-2,2),B3点坐标为(-4,0),
B4点坐标为(-4,-4),B5点坐标为(0,-8),
B6点坐标为(8,-8),B7点坐标为(16,0)
B8点坐标为(16,16),B9点坐标为(0,32),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的倍,
∵2020÷8=252…4,
∴B2020的纵横坐标符号与点B4的相同,纵横坐标都是负值,
∴B2012的坐标为(-21010,
-21010).
故答案为:D.
9.【答案】
B
解:
点
与点B关于AE对称,
与
关于AE对称,
,
,
故
正确;
如图,连接
.
则
,
,
.
则
,
即
为直角三角形.
为
的中位线,
,
∽
,
,
即
,
故FB
.
.
为等腰直角三角形.
故
正确.
设
度,
度,
则在四边形
中,
,
即
度.
又
,
.
故
正确.
假设
成立,
则
,
,
为等边三角形,
故B
,与
矛盾,
故
错误.
故答案为:B.
10.【答案】
C
解:①∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=90°,
在△ABE和△BCF中,
∵
,
∴△ABE≌△BCF(SAS),
∴AE=BF,
故①符合题意;
②由①知:△ABE≌△BCF,
∴∠FBC=∠BAE,
∴∠FBC+∠ABF=∠BAE+∠ABF=90°,
∴AE⊥BF,
故②符合题意;
③∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BD=
BC,
∴CE+CF=CE+BE=
=
BC,
故③不符合题意;
④∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,
在△OBE和△OCF中,
∵
,
∴△OBE≌△OCF(SAS),
∴S△OBE=S△OCF
,
∴S四边形OECF=S△COE+S△OCF=S△COE+S△OBE=S△OBC=
S正方形ABCD
,
故④符合题意;
故答案为:C.
二、填空题
11.【答案】
1
解:∵四边形ABD是正方形,
∴OA=OB,∠OAE=∠OBF=45°,AC⊥BD,
∴∠AOB=90°,
∵OE⊥OF,∴∠EOF=90°,
∴∠AOE=∠BOF,
∴△AOE≌△BOF(ASA),
∴△AOE的面积=△BOF的面积,
∴四边形AFOE的面积=
正方形ABCD的面积=
×22=1;
故答案为:1.
12.【答案】
20
解:如图,
由题意得:
S四边形ABCD(阴影部分)=a2+b2-S△ADE-S△ABF
=a2+b2-
a2-
=
=
=
=20,
故答案为:20.
13.【答案】
解:过点B作
于E,
于F
∵ABCD为正方形
∴AB=BC,
∴
∴
∵
∴
∴AE=BF=5
∵BE=3
∴
故答案为:
.
14.【答案】
解:这是一个”将军饮马“类型的两条线段之和的最小值问题,可作点E关于AC的对称点F,连接BF,则BF的长就是PE+PF的最小值.
如图,在AD取一点F,使AF=AE,连接BF,则BF的长就是PE+PF的最小值,
在Rt△ABF中,AB=10,AF=AE=10-4=6,由勾股定理得:
.
故答案为
.
15.【答案】
图,延长FP、EP交AB、AD于M、N,∵四边形ABCD为正方形,∴∠PBE=∠PDF=45°,∴BE=PE=PM=1,PN=FD=FP=3,则?.
16.【答案】
3或
解:分两种情况:①当∠EFC=90°,如图1,
∵∠AFE=∠B=90°,∠EFC=90°,
∴点A、F、C共线,
∵矩形ABCD的边AD=4,
∴BC=AD=4,
在Rt△ABC中,AC=
设BE=x,则CE=BC-BE=4-x,
由翻折的性质得AF=AB=3,EF=BE=x,∴CF=AC-AF=5-3=2
在Rt△CEF中,EF2+CF2=CE2
,
即x2+22=(4-x)2
,
解得x=
;
②当∠CEF=90°,如图2
由翻折的性质可知∠AEB=∠AEF=45°,
∴四边形ABEF是正方形,
∴BE=AB=3,
故BE的长为3或
.
故答案为:3或
.
17.【答案】
98
解:如图,
设AM=2a.BM=b.则正方形ABCD的面积=4a2+b2
由题意可知EF=(2a-b)-2(a-b)=2a-b-2a+2b=b,
∵AM=
EF,
∴2a=
b,
∴a=?
b,
∵正方形EFGH的面积为2,
∴b2=2,
∴正方形ABCD的面积=4a2+b2=49b2=98.
故答案为:98.
18.【答案】
①②④⑤
解:①②∵四边形ABCD是正方形,∴AB=AD
,
∠B=∠D=90°,∠BAD=90°,∵AE平分∠DAC
,
∴∠FAD=∠CAF=22.5°,∵BH=DF
,
∴△ABH≌△ADF
,
∴AH=AF
,
∠BAH=?FAD=22.5°,∴∠HAC=∠FAC
,
∴HM=FM
,
AC⊥FH
,
∵AE平分∠DAC
,
∴DF=FM
,
∴FH=2DF=2BH
,
故答案为:项①②正确;
③在Rt△FMC中,∠FCM=45°,∴△FMC是等腰直角三角形,∵正方形的边长为2,∴AC=
,MC=DF=
﹣2,∴FC=2﹣DF=2﹣(
﹣2)=4﹣
,S△AFC=
CF?AD≠1,所以选项③错误;
④AF=
=
=
,∵△ADF∽△CEF
,
∴
,∴
,∴CE=
,∴CE=
AF
,
故答案为:项④正确;
⑤在Rt△FEC中,EG⊥FC
,
∴
=FG?CG
,
cos∠FCE=
,∴CG=
=
=1,∴DG=CG
,
∴
=FG?DG
,
故答案为:项⑤正确;
本题正确的结论有4个,
故答案为:①②④⑤.
三、解答题
19.【答案】
证明:如图,作
于点M,
∵四边形
是矩形,∴
,∴
,
∴
,
,∠ABC=90°
∵
,∴
,
∵
,∴
,
∴
,∴
∴矩形
是正方形.
20.【答案】
解:由题意得:
?
?
21.【答案】
证明:∵四边形ABCD是正方形,
∴AC⊥BD,OC=OD,
∴∠DOG=∠EOC=90°,∠OCE+∠CED=90°
∵DF⊥CE,
∴∠EDF+∠CED=90°
∴∠EDF=∠OEC
∴△DOG≌△COE(ASA)
∴OE=OG
22.【答案】解:(1)连接BD交AC于O,
∵
,
,
∴△BPQ为等腰直角三角形,
∴当BP最短即BP⊥AC,△BPQ的面积最小,此时P为AC的中点O,
∵四边形ABCD是边长为2的正方形,
∴BD=
AB=2
,
∴BO=
,即BP=
,
∴△BPQ的最小面积为
=1,
故答案为:1;
(2)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵BP⊥BQ,
∴∠CBQ+∠PBC=90°,
∴∠ABP=∠CBQ,又BP=BQ,
∴△ABP≌△CBQ(SAS),
∴CQ=AP
(3)解:PF=EQ,理由为:
作PM⊥AB,PN⊥AD,GQ⊥BC,垂足分别为M、N、G,则∠PNF=∠QGE=90°,
在正方形ABCD中,AC平分∠DAB,AD∥BC,
∴PN=PM,∠NFP=∠GEQ,
∵△ABP≌△CBQ,
∴PM=QG,
∴PN=QG,
在△NFP和△GEQ中,
,
∴△NFP≌△GEQ(AAS),
∴PF=EQ.
23.【答案】
(1)
(2)解:OE=OF;证明如下:
∵四边形
为正方形,对角线AC、BD相交于点
,
,
∴
∴
于点
,
,
在
和
中
∴OE=OF.
解:(1)
;
∵正方形ABCD的对角线AC、BD相交于点O,
∴OA=OD,OA⊥OD,
∵AM⊥DE,
∴∠EAM+∠AEM=∠EDO+∠AEM=90°,
∴∠EAM=∠EDO,
在△FAO和△EDO中,
,
∴△FAO≌△EDO,
∴OE=OF.
24.【答案】
(1)
(2)解:如图②,取AD的中点M,连接PM,
∵四边形ABCD为∠ADC=120°的菱形,
∴BD=AD,∠DAP=30°,∠ADP=∠CDP=60°,
∴△MDP是等边三角形,
∴PM=PD,∠PME=∠PDF=60°,
∵∠PAM=30°,
∴∠MPD=60°,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中
,
∴△MPE≌△DPF(ASA)
∴ME=DF,
∴DE+DF=
AD;
(3)解:如图③,
当点E落在AD的延长线上时,取AD的中点M,连接PM,
∵四边形ABCD为菱形,∠ADC=120°,
∴AD=CD,∠DAP=30°,AC⊥BD,
∴∠ADP=∠CDP=60°,
∵AM=MD,
∴PM=MD,
∴△MDP是等边三角形,
∴∠PME=∠MPD=60°,PM=PD,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中
,
∴△MPE≌△DPF(ASA),
∴ME=DF,
∴DF?DE=ME?DE=DM=
AD.
解:(1)正方形ABCD的对角线AC,BD交于点P,
∴PA=PD,∠PAE=∠PDF=45°,
∵∠APE+∠EPD=∠DPF+∠EPD=90°,
∴∠APE=∠DPF,
在△APE和△DPF中
,
∴△APE≌△DPF(ASA),
∴AE=DF,
∴DE+DF=AD;
25.【答案】
(1)解:MN与AE的关系:MN⊥AE,MN=
AE.
证明:连接EN,并延长交AD于H.
∵四边形ABCD和四边形BEFG都是正方形,
∴EF//BG,AD//BC,EF=BE,AD=AB,
∴AD//EF,
∴∠HDN=∠EFN.
∵N是DF的中点,
∴DN=NF,
在△DHN和△FEN中,
,
∴△DHN≌△FEN,
∴HD=EF,
∴HD=BE,
∴AH=AE,
∵M是AE的中点,N是DF的中点,
∴MN是△AHE的中位线,
∴MN//AD,MN=
AD,
∵AD⊥AB,
∴MN⊥AB,
∴MN⊥AE,MN=
AE
(2)解:成立.
证明:如图,连接AN,BF,NE,GN,取AG中点H,连接NH.
∵H是AG中点,N是DF中点,
∴NH//AD.
∵AD⊥AB,
∴NH⊥AG,
在△ANH和△GNH中,
,
∴△ANH≌△GNH,
∴AN=GN,
∠ANH=GNH.
∵∠GBF=45°,
∠GBD=45°,
∴B,F,D共线,
∵∠BFG=∠BFE=45°,
∴∠GFN=∠EFN=135°,
在△GNF和△ENF中,
,
∴△GNF≌△ENF,
∴EN=GN,
∠GNF=∠ENF,
∵∠GHN=∠HGF=90°,
∠GFN=135°,
∴∠HNF=360°-90°-90°-135°=45°,
∴∠ANE=90°,
∵EN=GN,
AN=GN,
∴AN=EN,
∴△ANE是等腰直角三角形,
∵M是AE中点,
∴MN⊥AE,MN=
AE
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
初中数学苏科版八年级下册9.4
正方形的性质和判定
同步训练
一、单选题(本题共10题,每题3分,共30分)
1.以下命题中正确的是(?
)
A.?对角线相等的平行四边形是正方形??????????????????????
B.?对角线互相垂直的平行四边形是正方形
C.?对角线相等且互相平分的四边形是正方形???????????D.?对角线相等且互相垂直平分的四边形是正方形
2.如图,正方形ABCD的面积为8,菱形AECF的面积为4,则EF的长是(???
)
A.?4??????????????????????????????????????????B.???????????????????????????????????????????C.?2??????????????????????????????????????????D.?1
3.边长分别为2和4的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为(??
)
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?12
4.如图,正方形
的边长为
,
,
,连接
,则线段
的长为(??
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
5.如图,在正方形ABCD中,BD=2,∠DCE是正方形ABCD的外角,P是∠DCE的角平分线CF上任意一点,则△PBD的面积等于( )
A.?1??????????????????????????????????????????B.?1.5??????????????????????????????????????????C.?2??????????????????????????????????????????D.?2.5
6.正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FC过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积(
???)
A.?先变大后变小???????????????????????B.?先变小后变大???????????????????????C.?一直变大???????????????????????D.?保持不变
7.如图,正方形
和正方形
中,点D在
上,
,
,H是
的中点,那么
的长是(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
8.如图,在平面直角坐标系中有一边长为
的正方形
,边
,
分别在
?轴、
轴上,如果以对角线
为边作第二个正方形
,再以对角线
为边作第三个正方形
,照此规律作下去,则点
的坐标为(???
)
A.???????????B.???????????C.???????????D.?
9.在正方形ABCD中,点E为BC边的中点,点
与点B关于AE对称,
与AE交于点F,连接
,
,
下列结论:
;
为等腰直角三角形;
;
其中正确的是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
10.如图,在正方形ABCD中,AC、BD相交于点O,E、F分别为BC、CD上的两点,BE=CF,AE、BF分别交BD、AC于M、N两点,连OE、OF.下列结论:①AE=BF;②AE⊥BF;③CE+CF=BD;④S四边形OECF=
S正方形ABCD
,
其中正确的是(
??????????)
A.?①②?????????????????????????????????B.?①④?????????????????????????????????C.?①②④?????????????????????????????????D.?①②③④
二、填空题(本题共8题,每题2分,共16分)
11.如图,正方形
的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且
,则四边形
的面积为________.
12.如图,两个正方形的边长分别为
、
,若
,
,则四边形
(阴影部分)的面积为________
13.如图,在正方形
中,直线
分别过
三点且
,若
与
的距离为
,
与
的距离为
,则正方形
的边长是________.
14.如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是________cm.
15.如图,在正方形ABCD中,P为对角线BD上一点,过P作PE⊥BC于E,PF⊥CD于F,若PE=1,PF=3,则AP=________?。
16.如图,矩形纸片
中,已知
,
,点
在
边上,沿
折叠纸片,使点
落在点
处,连结
,当
为直角三角形时,
的长为________.
17.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为2的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=4
EF,则正方形ABCD的面积为________
18.如图,边长为2的正方形ABCD中,AE平分∠DAC
,
AE交CD于点F
,
CE⊥AE
,
垂足为点E
,
EG⊥CD
,
垂足为点G
,
点H在边BC上,BH=DF
,
连接AH、FH
,
FH与AC交于点M
,
以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=
AF;⑤EG2=FG?DG
,
其中正确结论的有________(只填序号).
三、解答题(本题共7题,共84分)
19.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),
,且
.求证:四边形ABCD是正方形.
20.正方形ABCD和正方形CEFG的边长分别为b和a将它们如图所示放置,求图中阴影部分的面积.
21.如图,正方形ABCD的对角线AC,BD相交于点O.E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OG=OE.
22.如图,边长为2的正方形ABCD中,P是对角线AC上的一个动点(点P不与A、C重合),连结BP,过点B作
且使得
,连结QP交BC于点E,延长QP与直线AD交于点F.
(1)
面积的最小值为________;
(2)连结CQ,求证:
;
(3)猜想PF与EQ的数量关系,并说明理由.
23.如图(1),正方形
的对角线
相交于点
是
上一点,连接
过点A作
垂足为
与
相交于点F.
(1)直接写出
与
的数量关系;
(2)如图(2)若点E在
的延长线上,
于点
交
的延长线于点F,其他条件不变.试探究
与
的数量关系,并说明理由.
24.如图①,
的顶点P在正方形
两条对角线的交点处,
,将
绕点P旋转,旋转过程中
的两边分别与正方形
的边
和
交于点E和点F(点F与点C、D不重合).
(1)如图①,当
时,
、
、
之间满足的数量关系是________;
(2)如图②,将图①中的正方形
改为
的菱形,其他条件不变,当
时,(1)中的结论变为
,并给出证明过程;
(3)在(2)的条件下,若旋转过程中
的边
与边
的延长线交于点E,其他条件不变,探究在整个运动变化过程中,
、
、
之间满足的数量关系,直接写出结论,不用加以证明.
25.如图1,点E是正方形ABCD边AB上任意一点,以BE为边作正方形BEFG
,
连接DF
,
点M
,
N分别是线段AE、DF中点,连接MN
.
(1)请猜想MN与AE的关系,并证明你的结论;
(2)把图1中的正方形BEFG绕点B顺时针旋转
,此时点E、G恰好分别落在线段BC、AB上,如图2,其他条件不变,(1)中的结论是否成立?请说明理由.
答案解析部分
一、单选题
1.【答案】
D
解:A、对角线相等的平行四边形是矩形,故不符合题意;
B、对角线互相垂直的平行四边形是菱形,故不符合题意;
C、对角线相等且互相平分的四边形是矩形,故不符合题意;
D、对角线相等且互相垂直平分的四边形是正方形,符合题意,
故答案为:D.
2.【答案】
C
解:连接AC,如下图所示:
∵正方形ABCD的面积为8
∴AD=
∴在Rt△ACD中,由勾股定理知:
,
∵菱形AECF的面积为4,
∴
×EF×AC=4,代入AC=4,
故求得EF=2.
故答案选:C.
3.【答案】
B
解:如图,
∵BC=4,CE=2,
∴BE=2,
∴BE=
BC,
∵边长分别为2和4的两个正方形按如图的样式摆放并连线,
∴ER//CQ,
∴ER为△BCQ的中位线,
∴ER=
CQ=1,
∴S阴影=S△ABQ-S△BER=
AB·BC-
BE·ER=
×4×4-
×2×1=7,
故答案为:B.
4.【答案】
B
解:如图,延长
交
于点
,
,
,
,
,
和
是直角三角形,
在
和
中,
,
,
,
,
,
,
又
,
,
,
,
在
和
中,
,
,
,
,
,
,
同理可得
,
在
中,
,
故答案为:B.
5.【答案】
A
CG⊥BD于G,
∵CF是∠DCE的平分线,
∴∠FCE=45°,
∵∠DBC=45°,
∴CF∥BD,
∴CG等于△PBD的高,
∵BD=2,
∴CG=1,
△PBD的面积等于=1.
故答案为:A.
6.【答案】
D
解:连接DE,
∵S△CDE=S四边形CEGF,S△CDE=S正方形ABCD
,
∴S四边形CEGF=S正方形ABCD
,
故答案为:D.
7.【答案】
B
解:如图,连接AC、CF,
在正方形ABCD和正方形CEFG中,AC=
BC=2
,CF=
CE=6
,
∠ACD=∠GCF=45°,
所以,∠ACF=45°+45°=90°,
所以,△ACF是直角三角形,
由勾股定理得,AF=
=4
,
∵H是AF的中点,
∴CH=
AF=
×4
=2
.
故答案为:B.
8.【答案】
D
解:
∵正方形OABC边长为1,
∴OB=,
∴OB1=2,
∴B1点坐标为(0,2),
同理可知B2点坐标为(-2,2),B3点坐标为(-4,0),
B4点坐标为(-4,-4),B5点坐标为(0,-8),
B6点坐标为(8,-8),B7点坐标为(16,0)
B8点坐标为(16,16),B9点坐标为(0,32),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的倍,
∵2020÷8=252…4,
∴B2020的纵横坐标符号与点B4的相同,纵横坐标都是负值,
∴B2012的坐标为(-21010,
-21010).
故答案为:D.
9.【答案】
B
解:
点
与点B关于AE对称,
与
关于AE对称,
,
,
故
正确;
如图,连接
.
则
,
,
.
则
,
即
为直角三角形.
为
的中位线,
,
∽
,
,
即
,
故FB
.
.
为等腰直角三角形.
故
正确.
设
度,
度,
则在四边形
中,
,
即
度.
又
,
.
故
正确.
假设
成立,
则
,
,
为等边三角形,
故B
,与
矛盾,
故
错误.
故答案为:B.
10.【答案】
C
解:①∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=90°,
在△ABE和△BCF中,
∵
,
∴△ABE≌△BCF(SAS),
∴AE=BF,
故①符合题意;
②由①知:△ABE≌△BCF,
∴∠FBC=∠BAE,
∴∠FBC+∠ABF=∠BAE+∠ABF=90°,
∴AE⊥BF,
故②符合题意;
③∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BD=
BC,
∴CE+CF=CE+BE=
=
BC,
故③不符合题意;
④∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,
在△OBE和△OCF中,
∵
,
∴△OBE≌△OCF(SAS),
∴S△OBE=S△OCF
,
∴S四边形OECF=S△COE+S△OCF=S△COE+S△OBE=S△OBC=
S正方形ABCD
,
故④符合题意;
故答案为:C.
二、填空题
11.【答案】
1
解:∵四边形ABD是正方形,
∴OA=OB,∠OAE=∠OBF=45°,AC⊥BD,
∴∠AOB=90°,
∵OE⊥OF,∴∠EOF=90°,
∴∠AOE=∠BOF,
∴△AOE≌△BOF(ASA),
∴△AOE的面积=△BOF的面积,
∴四边形AFOE的面积=
正方形ABCD的面积=
×22=1;
故答案为:1.
12.【答案】
20
解:如图,
由题意得:
S四边形ABCD(阴影部分)=a2+b2-S△ADE-S△ABF
=a2+b2-
a2-
=
=
=
=20,
故答案为:20.
13.【答案】
解:过点B作
于E,
于F
∵ABCD为正方形
∴AB=BC,
∴
∴
∵
∴
∴AE=BF=5
∵BE=3
∴
故答案为:
.
14.【答案】
解:这是一个”将军饮马“类型的两条线段之和的最小值问题,可作点E关于AC的对称点F,连接BF,则BF的长就是PE+PF的最小值.
如图,在AD取一点F,使AF=AE,连接BF,则BF的长就是PE+PF的最小值,
在Rt△ABF中,AB=10,AF=AE=10-4=6,由勾股定理得:
.
故答案为
.
15.【答案】
图,延长FP、EP交AB、AD于M、N,∵四边形ABCD为正方形,∴∠PBE=∠PDF=45°,∴BE=PE=PM=1,PN=FD=FP=3,则?.
16.【答案】
3或
解:分两种情况:①当∠EFC=90°,如图1,
∵∠AFE=∠B=90°,∠EFC=90°,
∴点A、F、C共线,
∵矩形ABCD的边AD=4,
∴BC=AD=4,
在Rt△ABC中,AC=
设BE=x,则CE=BC-BE=4-x,
由翻折的性质得AF=AB=3,EF=BE=x,∴CF=AC-AF=5-3=2
在Rt△CEF中,EF2+CF2=CE2
,
即x2+22=(4-x)2
,
解得x=
;
②当∠CEF=90°,如图2
由翻折的性质可知∠AEB=∠AEF=45°,
∴四边形ABEF是正方形,
∴BE=AB=3,
故BE的长为3或
.
故答案为:3或
.
17.【答案】
98
解:如图,
设AM=2a.BM=b.则正方形ABCD的面积=4a2+b2
由题意可知EF=(2a-b)-2(a-b)=2a-b-2a+2b=b,
∵AM=
EF,
∴2a=
b,
∴a=?
b,
∵正方形EFGH的面积为2,
∴b2=2,
∴正方形ABCD的面积=4a2+b2=49b2=98.
故答案为:98.
18.【答案】
①②④⑤
解:①②∵四边形ABCD是正方形,∴AB=AD
,
∠B=∠D=90°,∠BAD=90°,∵AE平分∠DAC
,
∴∠FAD=∠CAF=22.5°,∵BH=DF
,
∴△ABH≌△ADF
,
∴AH=AF
,
∠BAH=?FAD=22.5°,∴∠HAC=∠FAC
,
∴HM=FM
,
AC⊥FH
,
∵AE平分∠DAC
,
∴DF=FM
,
∴FH=2DF=2BH
,
故答案为:项①②正确;
③在Rt△FMC中,∠FCM=45°,∴△FMC是等腰直角三角形,∵正方形的边长为2,∴AC=
,MC=DF=
﹣2,∴FC=2﹣DF=2﹣(
﹣2)=4﹣
,S△AFC=
CF?AD≠1,所以选项③错误;
④AF=
=
=
,∵△ADF∽△CEF
,
∴
,∴
,∴CE=
,∴CE=
AF
,
故答案为:项④正确;
⑤在Rt△FEC中,EG⊥FC
,
∴
=FG?CG
,
cos∠FCE=
,∴CG=
=
=1,∴DG=CG
,
∴
=FG?DG
,
故答案为:项⑤正确;
本题正确的结论有4个,
故答案为:①②④⑤.
三、解答题
19.【答案】
证明:如图,作
于点M,
∵四边形
是矩形,∴
,∴
,
∴
,
,∠ABC=90°
∵
,∴
,
∵
,∴
,
∴
,∴
∴矩形
是正方形.
20.【答案】
解:由题意得:
?
?
21.【答案】
证明:∵四边形ABCD是正方形,
∴AC⊥BD,OC=OD,
∴∠DOG=∠EOC=90°,∠OCE+∠CED=90°
∵DF⊥CE,
∴∠EDF+∠CED=90°
∴∠EDF=∠OEC
∴△DOG≌△COE(ASA)
∴OE=OG
22.【答案】解:(1)连接BD交AC于O,
∵
,
,
∴△BPQ为等腰直角三角形,
∴当BP最短即BP⊥AC,△BPQ的面积最小,此时P为AC的中点O,
∵四边形ABCD是边长为2的正方形,
∴BD=
AB=2
,
∴BO=
,即BP=
,
∴△BPQ的最小面积为
=1,
故答案为:1;
(2)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵BP⊥BQ,
∴∠CBQ+∠PBC=90°,
∴∠ABP=∠CBQ,又BP=BQ,
∴△ABP≌△CBQ(SAS),
∴CQ=AP
(3)解:PF=EQ,理由为:
作PM⊥AB,PN⊥AD,GQ⊥BC,垂足分别为M、N、G,则∠PNF=∠QGE=90°,
在正方形ABCD中,AC平分∠DAB,AD∥BC,
∴PN=PM,∠NFP=∠GEQ,
∵△ABP≌△CBQ,
∴PM=QG,
∴PN=QG,
在△NFP和△GEQ中,
,
∴△NFP≌△GEQ(AAS),
∴PF=EQ.
23.【答案】
(1)
(2)解:OE=OF;证明如下:
∵四边形
为正方形,对角线AC、BD相交于点
,
,
∴
∴
于点
,
,
在
和
中
∴OE=OF.
解:(1)
;
∵正方形ABCD的对角线AC、BD相交于点O,
∴OA=OD,OA⊥OD,
∵AM⊥DE,
∴∠EAM+∠AEM=∠EDO+∠AEM=90°,
∴∠EAM=∠EDO,
在△FAO和△EDO中,
,
∴△FAO≌△EDO,
∴OE=OF.
24.【答案】
(1)
(2)解:如图②,取AD的中点M,连接PM,
∵四边形ABCD为∠ADC=120°的菱形,
∴BD=AD,∠DAP=30°,∠ADP=∠CDP=60°,
∴△MDP是等边三角形,
∴PM=PD,∠PME=∠PDF=60°,
∵∠PAM=30°,
∴∠MPD=60°,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中
,
∴△MPE≌△DPF(ASA)
∴ME=DF,
∴DE+DF=
AD;
(3)解:如图③,
当点E落在AD的延长线上时,取AD的中点M,连接PM,
∵四边形ABCD为菱形,∠ADC=120°,
∴AD=CD,∠DAP=30°,AC⊥BD,
∴∠ADP=∠CDP=60°,
∵AM=MD,
∴PM=MD,
∴△MDP是等边三角形,
∴∠PME=∠MPD=60°,PM=PD,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中
,
∴△MPE≌△DPF(ASA),
∴ME=DF,
∴DF?DE=ME?DE=DM=
AD.
解:(1)正方形ABCD的对角线AC,BD交于点P,
∴PA=PD,∠PAE=∠PDF=45°,
∵∠APE+∠EPD=∠DPF+∠EPD=90°,
∴∠APE=∠DPF,
在△APE和△DPF中
,
∴△APE≌△DPF(ASA),
∴AE=DF,
∴DE+DF=AD;
25.【答案】
(1)解:MN与AE的关系:MN⊥AE,MN=
AE.
证明:连接EN,并延长交AD于H.
∵四边形ABCD和四边形BEFG都是正方形,
∴EF//BG,AD//BC,EF=BE,AD=AB,
∴AD//EF,
∴∠HDN=∠EFN.
∵N是DF的中点,
∴DN=NF,
在△DHN和△FEN中,
,
∴△DHN≌△FEN,
∴HD=EF,
∴HD=BE,
∴AH=AE,
∵M是AE的中点,N是DF的中点,
∴MN是△AHE的中位线,
∴MN//AD,MN=
AD,
∵AD⊥AB,
∴MN⊥AB,
∴MN⊥AE,MN=
AE
(2)解:成立.
证明:如图,连接AN,BF,NE,GN,取AG中点H,连接NH.
∵H是AG中点,N是DF中点,
∴NH//AD.
∵AD⊥AB,
∴NH⊥AG,
在△ANH和△GNH中,
,
∴△ANH≌△GNH,
∴AN=GN,
∠ANH=GNH.
∵∠GBF=45°,
∠GBD=45°,
∴B,F,D共线,
∵∠BFG=∠BFE=45°,
∴∠GFN=∠EFN=135°,
在△GNF和△ENF中,
,
∴△GNF≌△ENF,
∴EN=GN,
∠GNF=∠ENF,
∵∠GHN=∠HGF=90°,
∠GFN=135°,
∴∠HNF=360°-90°-90°-135°=45°,
∴∠ANE=90°,
∵EN=GN,
AN=GN,
∴AN=EN,
∴△ANE是等腰直角三角形,
∵M是AE中点,
∴MN⊥AE,MN=
AE
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
