9.5 三角形的中位线 同步训练(含解析)
文档属性
| 名称 | 9.5 三角形的中位线 同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 07:13:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学苏科版八年级下册9.5
三角形的中位线
同步训练
一、单选题(本题共10题,每题3分,共30分)
1.Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为(????
)
A.?10cm????????????????????????????????????B.?3cm????????????????????????????????????C.?4cm????????????????????????????????????D.?5cm
2.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是(
??)
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?5
3.如图,Rt△ABC中,∠BAC=90°,点D
,
E分别是边AB
,
BC的中点,AD与CE交于点F
,
则△DEF与△ACF的面积之比是(???
)
A.?1:2????????????????????????????????????B.?1:3????????????????????????????????????C.?2:3????????????????????????????????????D.?1:4
4.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为(??
)
A.?32??????????????????????????????????????????B.?16??????????????????????????????????????????C.?8??????????????????????????????????????????D.?4
5.如图,在平行四边形ABCD中,已知
分别是线段OD,OA的中点,则EF的长为(??
)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?8
6.如图,在四边形ABCD中,∠C=90°,E,F分别为AB,AD的中点,BC=2,CD=
,则EF的长为(??
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
7.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,则应添加的条件是(???
)
A.?AB//CD?????????????????????????????B.?AC⊥BD?????????????????????????????C.?AC=BD?????????????????????????????D.?AD=BC
8.如图,在正方形ABCD中,AB=4,E是CD的中点,将
BCE沿BE翻折至
BFE,连接DF,则DF的长度是(??
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
9.矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连结AF,取AF的中点H,连结GH,若BC=EF=4,CD=CE=2,则GH=(
???)
A.?1?????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
10.如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有(??
)
A.?3个?????????????????????????????????????B.?4n个?????????????????????????????????????C.?3n个?????????????????????????????????????D.?3n个
二、填空题(本题共8题,每题2分,共16分)
11.如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是BO、BC的中点,若AB=5,BC=12,则EF=________;
12.如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN。若AB=5,BC=8,则MN=________。
13.如图所示,
为
的中位线,点F在
上,且
,若
则
的长为________.
14.如图,
ABC中,AB=AC=4,以AC为斜边作Rt
ADC,使∠ADC=90°,∠CAD=∠CAB=30°,E、F分别是BC、AC的中点,则ED=________.
15.如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为________.
16.如图,在四边形ABCD中,AD=BC
,
∠DAB=50°,∠CBA=70°,P、M、N分别是AB
,
AC、BD的中点,若BC=8,则△PMN的周长是________.
17.如图,△ABC的周长为26,点D、?E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长是________.
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN、MN的中点,则DE长度的取值范围是________.
三、解答题(本题共10题,共84分)
19.如图,在△ABC中,∠ACB=90°,点D
,
E
,
F分别为AB
,
AC
,
BC的中点.求证:CD=EF
.
20.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
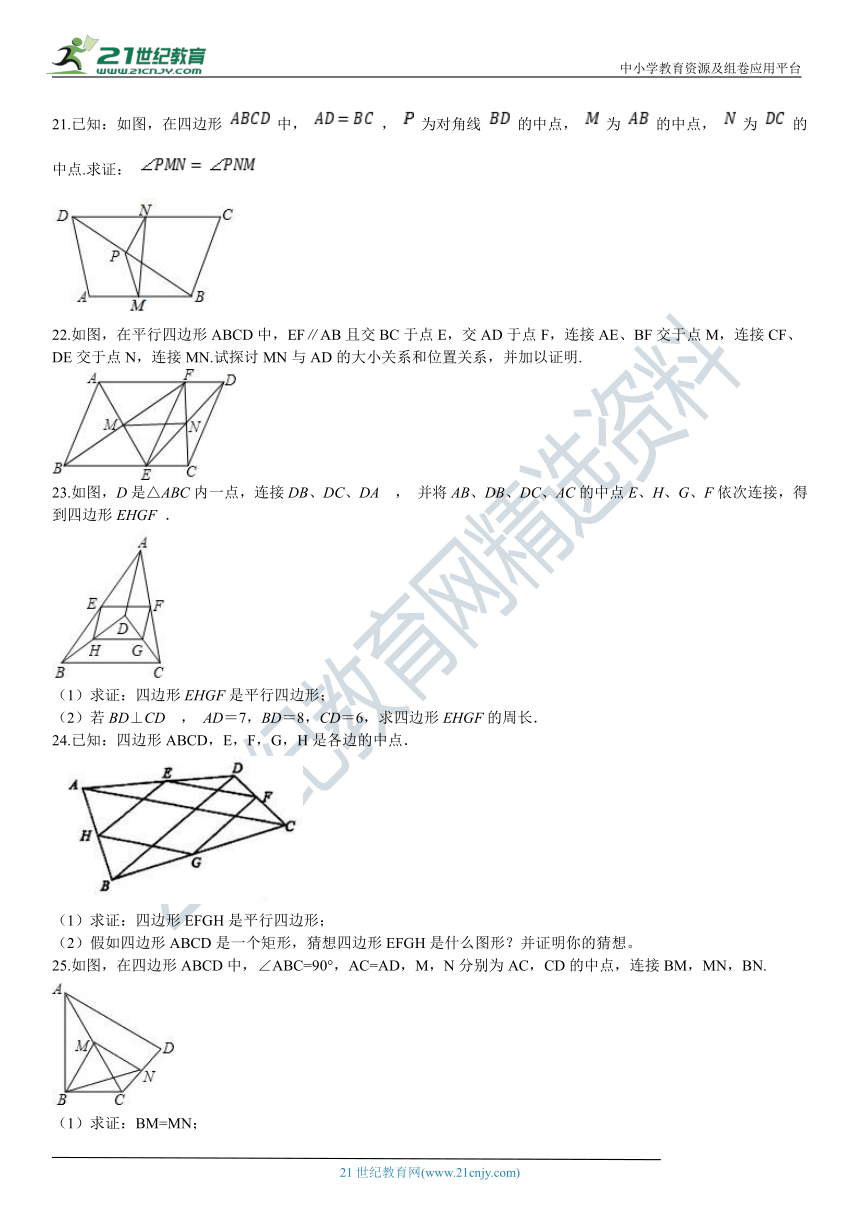
21.已知:如图,在四边形
中,
,
为对角线
的中点,
为
的中点,
为
的中点.求证:
22.如图,在平行四边形ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE、BF交于点M,连接CF、DE交于点N,连接MN.试探讨MN与AD的大小关系和位置关系,并加以证明.
23.如图,D是△ABC内一点,连接DB、DC、DA
,
并将AB、DB、DC、AC的中点E、H、G、F依次连接,得到四边形EHGF
.
(1)求证:四边形EHGF是平行四边形;
(2)若BD⊥CD
,
AD=7,BD=8,CD=6,求四边形EHGF的周长.
24.已知:四边形ABCD,E,F,G,H是各边的中点.
(1)求证:四边形EFGH是平行四边形;
(2)假如四边形ABCD是一个矩形,猜想四边形EFGH是什么图形?并证明你的猜想。
25.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
26.如图,点O是△ABC内一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G.
(1)判断四边形DEFG的形状,并说明理由;
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段BC的长.
27.如图,在R△ABC中,∠ACB=90°,点F是CB的中点,过点F作FE∥AC交AB于点E点D是CA延长线上的一点,且AD=
AC,连接DE、AF
(1)求证:四边形ADEF是平行四边形;
(2)若四边ADEF的周长是24cm,BC的长为6cm,求四边形ADEF的面积.
28.在菱形ABCD中,∠BAD=60°
(1)如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3)在(2)的条件下,若AC=
,请你直接写出DM+CN的最小值
答案解析部分
一、单选题
1.【答案】
D
解:∵Rt△ABC两直角边的长分别为6cm和8cm,
∴斜边=
=10cm,
∴连接这两条直角边中点的线段长为
×10=5cm.
故答案为:D.
2.【答案】
C
解:∵D、E分别是△ABC的边BC、AB的中点,
∴DE=
AC,同理
EF=
BC,DF=
AB,∴C△DEF=DE+EF+DF=
(AC+BC+AB)=
×20=10.
故答案为:C.
3.【答案】
D
解:∵点D
,
E分别是边AB
,
BC的中点,
∴DE∥AC
,
DE=
AC
,
∴△FDE∽△FAC
,
∴S△DEF:S△ACF=(DE:AC)2=1:4.
故答案为:D
.
4.【答案】
C
解:∵AD=AC
∴
是等腰三角形
∵AE⊥CD
∴
∴E是CD的中点
∵F是BC的中点
∴EF是△BCD的中位线
∴
故答案为:C.
5.【答案】
B
解:∵在平行四边形ABCD中,∠ODA=90°,AC=20,BD=12,
∴AO=CO=10,BO=DO=6,
故AD=
=
=8,
∵E、F分别是线段OD、OA的中点,
∴EF是△ADO的中位线,
∴EF∥AD,EF=
AD,
则EF的长为:4.
故答案为:B.
6.【答案】
D
解:连接BD,
∵BC=2,CD=
,∠C=90°,
∴BD=
=
,
∵E、F分别为AB、AD的中点,
∴BD=
EF=
,
故答案为:D.
7.【答案】
B
解:∵E、F、G、H是四边形各边中点,
∴易得四边形EFGH是平行四边形,
当AC⊥BD时,四边形EFGH是矩形.
故答案选B.
8.【答案】
D
解:如图,连接CF,交BE于H,
∵在正方形ABCD中,AB=4,E是CD的中点,
∴BC=CD=4,CE=DE=2,∠BCD=90°,
∴BE=
,
∵将△BCE沿BE翻折至△BFE,
∴CE=EF=2,BE⊥CF,FH=CH,
∵S△BCE=
×BE×CH=
×BC×CE,
∴CH=
,
∴EH=
,
∵CE=DE,FH=CH,
∴DF=2EH=
,
故答案为:D.
9.【答案】
C
解:解法一:以C点为原点建立直角坐标系,CE为x正半轴,CG为y正半轴,
则A(-4,2),F(2,4),G(0,4);
∵H为AF的中点,则xH=,
yH=?
则H的坐标为(1,3),
∴.
解法二:作HL⊥FE,HM⊥BE,DN⊥FE,
?,
,
?.
故答案为:C.
?
10.【答案】
D
解:图(1)中,?A1、B1、C1分别是△ABC的边BC、CA、AB的中点?,
∴?A1B1∥AB?,B1C1?∥BC,A1C1?∥AC,,
∴四边形AC1A1B1C1?,A1B1C1B,
A1CB1C1是平行四边形,共有3=3×1个;
图(2)中,同理可得AC1A1B1C1?,A1B1C1B,
A1CB1C1
,
A1C2B2C1分?A2B2
A1C2分
A2B2C2B1是平行四边形,共有6=2×3个;
···,依次规律,可得第n个图形中平行四边形的个数为3n个.
故答案为:D.
二、填空题
11.【答案】
解:∵四边形ABCD是矩形,
∴∠BAD=90°,OC=
AC,AD=BC=12,
∴AC=
=13,
∴OC=
,
∵点E、F分别是BO、BC的中点,
∴EF是△BOC的中位线,
∴EF=
OC=
,
故答案为:
.
12.【答案】
1.5
解:∵BD⊥AB,BM⊥AD于点M
∴AM=DM
∵N为AC的中点
∴AN=CN
∴MN为三角形ACD的中位线
∴MN=DC
∵AB=5,BC=8
∴DC=3
∴MN=
13.【答案】
3
解:∵
为
的中位线,
∴DE=
,点D为AB的中点
∵
∴DF=
∴EF=DE-DF=3
故答案为:3.
14.【答案】
解:∵E、F分别是BC、AC的中点,∠CAD=∠CAB=30°,∠ADC=90°,
∴EF是△ABC的中位线,CD=
AC,
∴EF=
AB,∠EFC=∠CAB=30°.
∵AB=AC,△ACD是直角三角形,点F是斜边AC的中点,
∴EF=DF=CF=CD=2,
∴△CDF是等边三角形,
∴∠DFC=60°,
∴∠DFC+∠EFC
=60°+30°=90°,
∴△EFD为等腰直角三角形,
∴DE=
,
故答案为
.
15.【答案】
12
解:如图,延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=8,BN=ND,
又∵M是△ABC的边BC的中点,
∴MN是△BCD的中位线,
∴DC=2MN=4,
∴AC=AD+CD=8+4=12,
故答案为:12.
16.【答案】
12
解:∵P、N是AB和BD的中点,
∴PN=
AD=
×8=4,PN∥AD,
∴∠NPB=∠DAB=50°,
同理,PM=4,∠MPA=∠CBA=70°,
∴PM=PN=4,∠MPN=180°-50°-70°=60°,
∴△PMN是等边三角形.
∴MN=PM=PN=4,
∴△PMN的周长是12,
故答案为:12.
17.【答案】
3
解:∵BQ平分∠ABC,BQ⊥AE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点Q是AE中点,点P是AD中点,
∴PQ是△ADE的中位线.
∵BE+CD=AB+AC=26-BC=26-10=16,
∴DE=BE+CD-BC=6,
∴PQ=DE=3.
故答案为C.
18.【答案】
解:作CH⊥AB于H,连接CM,
在Rt△ABC中,AB
5,
S△ABC
AC×BC
AB×CH,即
3×4
5×CH,
解得:CH
,
∵点D、E分别为CN、MN的中点,
∴DE是△MNC的中位线,
∴DE
CM,
当CM⊥AB时,CM最小,最小值为
,
当点M与点B重合时,CM最大,最大值为4,
∴
.
故答案为:
.
三、解答题
19.【答案】
解:根据直角三角形斜边中中线等于斜边的一半可得
,再根据中位线定理可得
,从而可以得到
20.【答案】
解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=6,GF=CF,
则BG=AB﹣AG=8﹣6=2.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=
BG=1.
21.【答案】
证明:∵
是
中点,
是
中点,
∴
是
的中位线,
∴
,
∵
是
中点,
是
中点,
∴
是
的中位线,
∴
,
∵
,
∴
,
∴
是等腰三角形,
∴
.
22.【答案】
MN=
AD,MN∥AD;
证明:∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∵EF∥AB,∴EF∥CD
∴四边形ABEF、四边形EFDC均是平行四边形,
∴AM=EM,FN=CN,
∴MN是△AED的中位线,
∴MN=
AD,MN∥AD.
23.【答案】
(1)证明:∵E、F分别是AB、AC的中点,
∴EF∥BC,EF=
BC.
∵H、G分别是DB、DC的中点,
∴HG∥BC,HG=
BC.
∴HG=EF,HG∥EF.
∴四边形EHGF是平行四边形
(2)解:∵BD⊥CD,BD=8,CD=6,
∴BC=
=
=10,
∵E、F、H、G分别是AB、AC、BD、CD的中点,
∴EH=FG=
AD=3.5,
EF=GH=
BC=5,
∴四边形EHGF的周长=EH+GH+FG+EF=17
24.【答案】
(1)∵E,F,G,H是各边的中点,
∴EF∥AC∥HG,HE∥BD∥GF,
∴四边形EFGH是平行四边形;???????????
(2)四边形ABCD是一个矩形,四边形EFGH是菱形;
∵四边形ABCD是矩形,
∴AC=BD,
∴EF=
AC=
=EH,
∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形.?????????????????
25.【答案】
(1)证明:在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,且MN=
AD,在Rt△ABC中,∵M是AC的中点,∴BM=
AC,又∵AC=AD,∴MN=BM;
(2)解:∵∠BAD=60°且AC平分∠BAD,∴∠BAC=∠DAC=30°,由(1)知,BM=
AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°.∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴
,而由(1)知,MN=BM=
AC=
×2=1,∴BN=
.
26.【答案】
(1)解:四边形DEFG是平行四边形,
理由如下:∵E、F分别为线段OB、OC的中点,
∴EF=
BC,EF∥BC,
同理DG=
BC,DG∥BC,
∴EF=DG,EF∥DG,
∴四边形DEFG是平行四边形
(2)解:∵∠OBC和∠OCB互余,
∴∠BOC=90°,
∵M为EF的中点,OM=2,
∴EF=2OM=4,
∴BC=2EF=8.
27.【答案】
(1)证明:∵点F是CB的中点,过点F作FE∥AC,
∴BE=AE,
∴EF=
AC,
∵AD=
AC,
∴EF=AD,
∵EF∥AD,
∴四边形ADEF是平行四边形;
(2)解:∵四边形ADEF的周长是24cm,
∴AD+AF=12,
∴AF=12-AD,
∵AC=2AD,CF=
BC=3,
∴AC2+CF2=AF2
,
即(2AD)2+9=(12-AD)2
,
∴AD=
-4,
∴四边形ADEF的面积=AD?CF=3
-12.
28.【答案】
(1)解:如图1,连接BD,则BD平分∠ABC,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠A+∠ABC=180?,
∵∠A=60?,
∴∠ABC=120?,
∴?ABD是等边三角形,
∴BD=AD=4,
∵E是AB的中点,
由勾股定理得:DE=2
,
∵DC∥AB,
∴∠EDC=∠DEA=90?,
在Rt?DEC中,
EC=2
(2)解:如图2,延长CD至H,使CD=DH,连接NH、AH,
∵AD=CD,
∴AD=DH,
∵CD∥AB,
∴∠HDA=∠BAD=60?,
∴?ADH是等边三角形,
∴AH=AD,
∠HAD=60?,
∵?AMN是等边三角形,
∴AM=AN,
∠NAM=60?,
∴∠HAN=∠DAM,
∴?ANH≌?AMD,
∴HN=DM,
∵D是CH的中点,Q是NC的中点,
∴DQ是?CHN的中位线,
∴HN=2DQ,
∴DM=2DQ
(3)解:如图2,由(2)知,HN=DM,
∴要CN+DM最小,便是CN+HN最小,
即:点C,H,N在同一条线上时,CN+DM最小,
此时,点D和点Q重合,
即:CN+DM的最小值为CH,
如图3,
由(2)知,△ADH是等边三角形,
∴∠H=60°.
∵AC是菱形ABCD的对角线,
∴∠ACD=
∠BCD=
∠BAD=30°,
∴∠CAH=180°-30°-60°=90°,
在Rt△ACH中,CH=
=2,
∴DM+CN的最小值为2
?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
初中数学苏科版八年级下册9.5
三角形的中位线
同步训练
一、单选题(本题共10题,每题3分,共30分)
1.Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为(????
)
A.?10cm????????????????????????????????????B.?3cm????????????????????????????????????C.?4cm????????????????????????????????????D.?5cm
2.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是(
??)
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?5
3.如图,Rt△ABC中,∠BAC=90°,点D
,
E分别是边AB
,
BC的中点,AD与CE交于点F
,
则△DEF与△ACF的面积之比是(???
)
A.?1:2????????????????????????????????????B.?1:3????????????????????????????????????C.?2:3????????????????????????????????????D.?1:4
4.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为(??
)
A.?32??????????????????????????????????????????B.?16??????????????????????????????????????????C.?8??????????????????????????????????????????D.?4
5.如图,在平行四边形ABCD中,已知
分别是线段OD,OA的中点,则EF的长为(??
)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?8
6.如图,在四边形ABCD中,∠C=90°,E,F分别为AB,AD的中点,BC=2,CD=
,则EF的长为(??
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
7.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,则应添加的条件是(???
)
A.?AB//CD?????????????????????????????B.?AC⊥BD?????????????????????????????C.?AC=BD?????????????????????????????D.?AD=BC
8.如图,在正方形ABCD中,AB=4,E是CD的中点,将
BCE沿BE翻折至
BFE,连接DF,则DF的长度是(??
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
9.矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连结AF,取AF的中点H,连结GH,若BC=EF=4,CD=CE=2,则GH=(
???)
A.?1?????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
10.如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有(??
)
A.?3个?????????????????????????????????????B.?4n个?????????????????????????????????????C.?3n个?????????????????????????????????????D.?3n个
二、填空题(本题共8题,每题2分,共16分)
11.如图,矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是BO、BC的中点,若AB=5,BC=12,则EF=________;
12.如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN。若AB=5,BC=8,则MN=________。
13.如图所示,
为
的中位线,点F在
上,且
,若
则
的长为________.
14.如图,
ABC中,AB=AC=4,以AC为斜边作Rt
ADC,使∠ADC=90°,∠CAD=∠CAB=30°,E、F分别是BC、AC的中点,则ED=________.
15.如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为________.
16.如图,在四边形ABCD中,AD=BC
,
∠DAB=50°,∠CBA=70°,P、M、N分别是AB
,
AC、BD的中点,若BC=8,则△PMN的周长是________.
17.如图,△ABC的周长为26,点D、?E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长是________.
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN、MN的中点,则DE长度的取值范围是________.
三、解答题(本题共10题,共84分)
19.如图,在△ABC中,∠ACB=90°,点D
,
E
,
F分别为AB
,
AC
,
BC的中点.求证:CD=EF
.
20.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
21.已知:如图,在四边形
中,
,
为对角线
的中点,
为
的中点,
为
的中点.求证:
22.如图,在平行四边形ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE、BF交于点M,连接CF、DE交于点N,连接MN.试探讨MN与AD的大小关系和位置关系,并加以证明.
23.如图,D是△ABC内一点,连接DB、DC、DA
,
并将AB、DB、DC、AC的中点E、H、G、F依次连接,得到四边形EHGF
.
(1)求证:四边形EHGF是平行四边形;
(2)若BD⊥CD
,
AD=7,BD=8,CD=6,求四边形EHGF的周长.
24.已知:四边形ABCD,E,F,G,H是各边的中点.
(1)求证:四边形EFGH是平行四边形;
(2)假如四边形ABCD是一个矩形,猜想四边形EFGH是什么图形?并证明你的猜想。
25.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
26.如图,点O是△ABC内一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G.
(1)判断四边形DEFG的形状,并说明理由;
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段BC的长.
27.如图,在R△ABC中,∠ACB=90°,点F是CB的中点,过点F作FE∥AC交AB于点E点D是CA延长线上的一点,且AD=
AC,连接DE、AF
(1)求证:四边形ADEF是平行四边形;
(2)若四边ADEF的周长是24cm,BC的长为6cm,求四边形ADEF的面积.
28.在菱形ABCD中,∠BAD=60°
(1)如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3)在(2)的条件下,若AC=
,请你直接写出DM+CN的最小值
答案解析部分
一、单选题
1.【答案】
D
解:∵Rt△ABC两直角边的长分别为6cm和8cm,
∴斜边=
=10cm,
∴连接这两条直角边中点的线段长为
×10=5cm.
故答案为:D.
2.【答案】
C
解:∵D、E分别是△ABC的边BC、AB的中点,
∴DE=
AC,同理
EF=
BC,DF=
AB,∴C△DEF=DE+EF+DF=
(AC+BC+AB)=
×20=10.
故答案为:C.
3.【答案】
D
解:∵点D
,
E分别是边AB
,
BC的中点,
∴DE∥AC
,
DE=
AC
,
∴△FDE∽△FAC
,
∴S△DEF:S△ACF=(DE:AC)2=1:4.
故答案为:D
.
4.【答案】
C
解:∵AD=AC
∴
是等腰三角形
∵AE⊥CD
∴
∴E是CD的中点
∵F是BC的中点
∴EF是△BCD的中位线
∴
故答案为:C.
5.【答案】
B
解:∵在平行四边形ABCD中,∠ODA=90°,AC=20,BD=12,
∴AO=CO=10,BO=DO=6,
故AD=
=
=8,
∵E、F分别是线段OD、OA的中点,
∴EF是△ADO的中位线,
∴EF∥AD,EF=
AD,
则EF的长为:4.
故答案为:B.
6.【答案】
D
解:连接BD,
∵BC=2,CD=
,∠C=90°,
∴BD=
=
,
∵E、F分别为AB、AD的中点,
∴BD=
EF=
,
故答案为:D.
7.【答案】
B
解:∵E、F、G、H是四边形各边中点,
∴易得四边形EFGH是平行四边形,
当AC⊥BD时,四边形EFGH是矩形.
故答案选B.
8.【答案】
D
解:如图,连接CF,交BE于H,
∵在正方形ABCD中,AB=4,E是CD的中点,
∴BC=CD=4,CE=DE=2,∠BCD=90°,
∴BE=
,
∵将△BCE沿BE翻折至△BFE,
∴CE=EF=2,BE⊥CF,FH=CH,
∵S△BCE=
×BE×CH=
×BC×CE,
∴CH=
,
∴EH=
,
∵CE=DE,FH=CH,
∴DF=2EH=
,
故答案为:D.
9.【答案】
C
解:解法一:以C点为原点建立直角坐标系,CE为x正半轴,CG为y正半轴,
则A(-4,2),F(2,4),G(0,4);
∵H为AF的中点,则xH=,
yH=?
则H的坐标为(1,3),
∴.
解法二:作HL⊥FE,HM⊥BE,DN⊥FE,
?,
,
?.
故答案为:C.
?
10.【答案】
D
解:图(1)中,?A1、B1、C1分别是△ABC的边BC、CA、AB的中点?,
∴?A1B1∥AB?,B1C1?∥BC,A1C1?∥AC,,
∴四边形AC1A1B1C1?,A1B1C1B,
A1CB1C1是平行四边形,共有3=3×1个;
图(2)中,同理可得AC1A1B1C1?,A1B1C1B,
A1CB1C1
,
A1C2B2C1分?A2B2
A1C2分
A2B2C2B1是平行四边形,共有6=2×3个;
···,依次规律,可得第n个图形中平行四边形的个数为3n个.
故答案为:D.
二、填空题
11.【答案】
解:∵四边形ABCD是矩形,
∴∠BAD=90°,OC=
AC,AD=BC=12,
∴AC=
=13,
∴OC=
,
∵点E、F分别是BO、BC的中点,
∴EF是△BOC的中位线,
∴EF=
OC=
,
故答案为:
.
12.【答案】
1.5
解:∵BD⊥AB,BM⊥AD于点M
∴AM=DM
∵N为AC的中点
∴AN=CN
∴MN为三角形ACD的中位线
∴MN=DC
∵AB=5,BC=8
∴DC=3
∴MN=
13.【答案】
3
解:∵
为
的中位线,
∴DE=
,点D为AB的中点
∵
∴DF=
∴EF=DE-DF=3
故答案为:3.
14.【答案】
解:∵E、F分别是BC、AC的中点,∠CAD=∠CAB=30°,∠ADC=90°,
∴EF是△ABC的中位线,CD=
AC,
∴EF=
AB,∠EFC=∠CAB=30°.
∵AB=AC,△ACD是直角三角形,点F是斜边AC的中点,
∴EF=DF=CF=CD=2,
∴△CDF是等边三角形,
∴∠DFC=60°,
∴∠DFC+∠EFC
=60°+30°=90°,
∴△EFD为等腰直角三角形,
∴DE=
,
故答案为
.
15.【答案】
12
解:如图,延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=8,BN=ND,
又∵M是△ABC的边BC的中点,
∴MN是△BCD的中位线,
∴DC=2MN=4,
∴AC=AD+CD=8+4=12,
故答案为:12.
16.【答案】
12
解:∵P、N是AB和BD的中点,
∴PN=
AD=
×8=4,PN∥AD,
∴∠NPB=∠DAB=50°,
同理,PM=4,∠MPA=∠CBA=70°,
∴PM=PN=4,∠MPN=180°-50°-70°=60°,
∴△PMN是等边三角形.
∴MN=PM=PN=4,
∴△PMN的周长是12,
故答案为:12.
17.【答案】
3
解:∵BQ平分∠ABC,BQ⊥AE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点Q是AE中点,点P是AD中点,
∴PQ是△ADE的中位线.
∵BE+CD=AB+AC=26-BC=26-10=16,
∴DE=BE+CD-BC=6,
∴PQ=DE=3.
故答案为C.
18.【答案】
解:作CH⊥AB于H,连接CM,
在Rt△ABC中,AB
5,
S△ABC
AC×BC
AB×CH,即
3×4
5×CH,
解得:CH
,
∵点D、E分别为CN、MN的中点,
∴DE是△MNC的中位线,
∴DE
CM,
当CM⊥AB时,CM最小,最小值为
,
当点M与点B重合时,CM最大,最大值为4,
∴
.
故答案为:
.
三、解答题
19.【答案】
解:根据直角三角形斜边中中线等于斜边的一半可得
,再根据中位线定理可得
,从而可以得到
20.【答案】
解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=6,GF=CF,
则BG=AB﹣AG=8﹣6=2.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=
BG=1.
21.【答案】
证明:∵
是
中点,
是
中点,
∴
是
的中位线,
∴
,
∵
是
中点,
是
中点,
∴
是
的中位线,
∴
,
∵
,
∴
,
∴
是等腰三角形,
∴
.
22.【答案】
MN=
AD,MN∥AD;
证明:∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∵EF∥AB,∴EF∥CD
∴四边形ABEF、四边形EFDC均是平行四边形,
∴AM=EM,FN=CN,
∴MN是△AED的中位线,
∴MN=
AD,MN∥AD.
23.【答案】
(1)证明:∵E、F分别是AB、AC的中点,
∴EF∥BC,EF=
BC.
∵H、G分别是DB、DC的中点,
∴HG∥BC,HG=
BC.
∴HG=EF,HG∥EF.
∴四边形EHGF是平行四边形
(2)解:∵BD⊥CD,BD=8,CD=6,
∴BC=
=
=10,
∵E、F、H、G分别是AB、AC、BD、CD的中点,
∴EH=FG=
AD=3.5,
EF=GH=
BC=5,
∴四边形EHGF的周长=EH+GH+FG+EF=17
24.【答案】
(1)∵E,F,G,H是各边的中点,
∴EF∥AC∥HG,HE∥BD∥GF,
∴四边形EFGH是平行四边形;???????????
(2)四边形ABCD是一个矩形,四边形EFGH是菱形;
∵四边形ABCD是矩形,
∴AC=BD,
∴EF=
AC=
=EH,
∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形.?????????????????
25.【答案】
(1)证明:在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,且MN=
AD,在Rt△ABC中,∵M是AC的中点,∴BM=
AC,又∵AC=AD,∴MN=BM;
(2)解:∵∠BAD=60°且AC平分∠BAD,∴∠BAC=∠DAC=30°,由(1)知,BM=
AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°.∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴
,而由(1)知,MN=BM=
AC=
×2=1,∴BN=
.
26.【答案】
(1)解:四边形DEFG是平行四边形,
理由如下:∵E、F分别为线段OB、OC的中点,
∴EF=
BC,EF∥BC,
同理DG=
BC,DG∥BC,
∴EF=DG,EF∥DG,
∴四边形DEFG是平行四边形
(2)解:∵∠OBC和∠OCB互余,
∴∠BOC=90°,
∵M为EF的中点,OM=2,
∴EF=2OM=4,
∴BC=2EF=8.
27.【答案】
(1)证明:∵点F是CB的中点,过点F作FE∥AC,
∴BE=AE,
∴EF=
AC,
∵AD=
AC,
∴EF=AD,
∵EF∥AD,
∴四边形ADEF是平行四边形;
(2)解:∵四边形ADEF的周长是24cm,
∴AD+AF=12,
∴AF=12-AD,
∵AC=2AD,CF=
BC=3,
∴AC2+CF2=AF2
,
即(2AD)2+9=(12-AD)2
,
∴AD=
-4,
∴四边形ADEF的面积=AD?CF=3
-12.
28.【答案】
(1)解:如图1,连接BD,则BD平分∠ABC,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠A+∠ABC=180?,
∵∠A=60?,
∴∠ABC=120?,
∴?ABD是等边三角形,
∴BD=AD=4,
∵E是AB的中点,
由勾股定理得:DE=2
,
∵DC∥AB,
∴∠EDC=∠DEA=90?,
在Rt?DEC中,
EC=2
(2)解:如图2,延长CD至H,使CD=DH,连接NH、AH,
∵AD=CD,
∴AD=DH,
∵CD∥AB,
∴∠HDA=∠BAD=60?,
∴?ADH是等边三角形,
∴AH=AD,
∠HAD=60?,
∵?AMN是等边三角形,
∴AM=AN,
∠NAM=60?,
∴∠HAN=∠DAM,
∴?ANH≌?AMD,
∴HN=DM,
∵D是CH的中点,Q是NC的中点,
∴DQ是?CHN的中位线,
∴HN=2DQ,
∴DM=2DQ
(3)解:如图2,由(2)知,HN=DM,
∴要CN+DM最小,便是CN+HN最小,
即:点C,H,N在同一条线上时,CN+DM最小,
此时,点D和点Q重合,
即:CN+DM的最小值为CH,
如图3,
由(2)知,△ADH是等边三角形,
∴∠H=60°.
∵AC是菱形ABCD的对角线,
∴∠ACD=
∠BCD=
∠BAD=30°,
∴∠CAH=180°-30°-60°=90°,
在Rt△ACH中,CH=
=2,
∴DM+CN的最小值为2
?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
