11.3 用反比例函数解决问题 同步训练(含解析)
文档属性
| 名称 | 11.3 用反比例函数解决问题 同步训练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 08:04:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学苏科版八年级下册11.3
用反比例函数解决问题
同步训练
一、单选题(本题共10题,每题3分,共30分)
1.一定质量的二氧化碳,当它的体积V=5,密度p=1.98kg/时,p与V
之间的函数关系式是(
?
?
?
)
A.?p=9.9V????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
2.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.?不小于0.5m3???????????????????B.?不大于0.5m3???????????????????C.?不小于0.6m3???????????????????D.?不大于0.6m3
3.如图,曲线表示温度T(℃)与时间t(h)之间的函数关系,它是一个反比例函数的图象的一支.当温度T≤2℃时,时间t应(??
)
A.?不小于
h??????????????????????B.?不大于
h??????????????????????C.?不小于
h??????????????????????D.?不大于
h
4.如图,直线y=-x+3与y轴交于点A,与反比例函数y=
(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为(??
)
A.?y=
???????????????????????????????B.?y=-
???????????????????????????????C.?y=
???????????????????????????????D.?y=-
5.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18°C的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(°C)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
(k≠0)的一部分,则当x=16时,大棚内的温度为(???
)
A.?18℃??????????????????????????????????B.?15.5℃??????????????????????????????????C.?13.5℃??????????????????????????????????D.?12℃
6.如图,在平面直角坐标系中,直线y=﹣
x+1分别交x轴,y轴于点A,B,交反比例函数y1=
(k<0,x<0),y2=
(k<0,x>0)于点C,D两点,连接OC,OD,过点D作DE⊥x轴于点E,若△ODE的面积与△OCB的面积相等,则k的值是(??
)
A.?﹣4???????????????????????????????????B.?﹣2???????????????????????????????????C.?﹣2
???????????????????????????????????D.?﹣
7.如图,在平面直角坐标系中,点
、
在函数
的图象上.当
时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D
.
QD交PA于点E
.
随着m的增大,四边形ACQE的面积(??
)
A.?减小???????????????????????????B.?增大???????????????????????????C.?先减小后增大???????????????????????????D.?先增大后减小
8.图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是(??
)
A.?当x=3时,EC<EM????????????????????????????????????????????B.?当y=9时,EC>EM
C.?当x增大时,EC·CF的值增大。?????????????????????????????D.?当y增大时,BE·DF的值不变。
9.如图,A,B两点在反比例函数
的图象上,C,D两点在反比例函数
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的值是(??
)
A.?6???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
10.如图,在直角坐标系中,直线
与坐标轴交于A、B两点,与双曲线
(
)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①
;②当0<x<3时,
;③如图,当x=3时,EF=
;④当x>0时,
随x的增大而增大,
随x的增大而减小.其中符合题意结论的个数是(
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题(本题共6题,每题2分,共12分)
11.在温度不变的条件下,一定质量的气体的压强P与它的体积V成反比例,当V=200时,P=50,则当P=25时,V=________.
12.某水池容积为300m3
,
原有水100m3
,
现以xm3/min的速度匀速向水池中注水,注满水需要y
min,则y关于x的函数表达式为________.
13.小刚欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为900牛顿和0.5米,则当动力臂为1.5米时,撬动石头需要的力大于________牛顿.(提示根据杠杆原理:阻力x阻力臂=动力x动力臂)
14.一次函数y1=k1x(k1≠0)与反比例函数y2=
(k2≠0)的图象的一个交点是M(-3,2),若y2________。
15.已知直线
与反比例函数
的图象交于A、B两点,当线段AB的长最小时,以AB为斜边作等腰直角三角形△ABC,则点C的坐标是________.
16.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为6mg.研究表明当每立方米空气中含药量低于1.2mg时,对人体方能无毒害作用,那么从消毒开始,至少需要经过________分钟后,学生才能回到教室.
三、综合题(本题共10题,共88分)
17.已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为ν(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时)
(1)求v关于t的函数表达式
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
18.码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地开始卸货,平均卸货速度v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上货物不超过5天卸货完毕,那么平均每天至少要缷货多少吨?
19.记面积为
的平行四边形的一条边长为x(cm),这条边上的高线长为y(cm).
(1)求y关于x的函数表达式,以及自变量x的取值范围.
(2)求当边长满足
时,高线长的最大值.
20.某校绿色行动小组组织一批人参加植树活动,完成任务的时间y(h)是参加植树人数
(人)的反比例函数,且当
人时,
.
(1)若平均每人每小时植树4棵,则这次共计要植树________棵;
(2)当
时,求y的值;
(3)为了能在
内完成任务,至少需要多少人参加植树?
21.某气球内充满一定质量的气体,当温度不变时,气球内气体的压强p(kPa)与气体的体积v(m?)成反比例。当气体的体积V=0.8m3时,气球内气体的压强p=112.5kPa。当气球内气体的压强大于150kPa时,气球就会爆炸。
(1)求p关于V的函数表达式。
(2)当气球内气体的体积从1.2m?增加至1.8
m?
(含1.2
m?和1.8m?)时,求气体压强的范围。
(3)若气球内气体的体积为0.55m?,气球会不会爆炸?请说明理由。
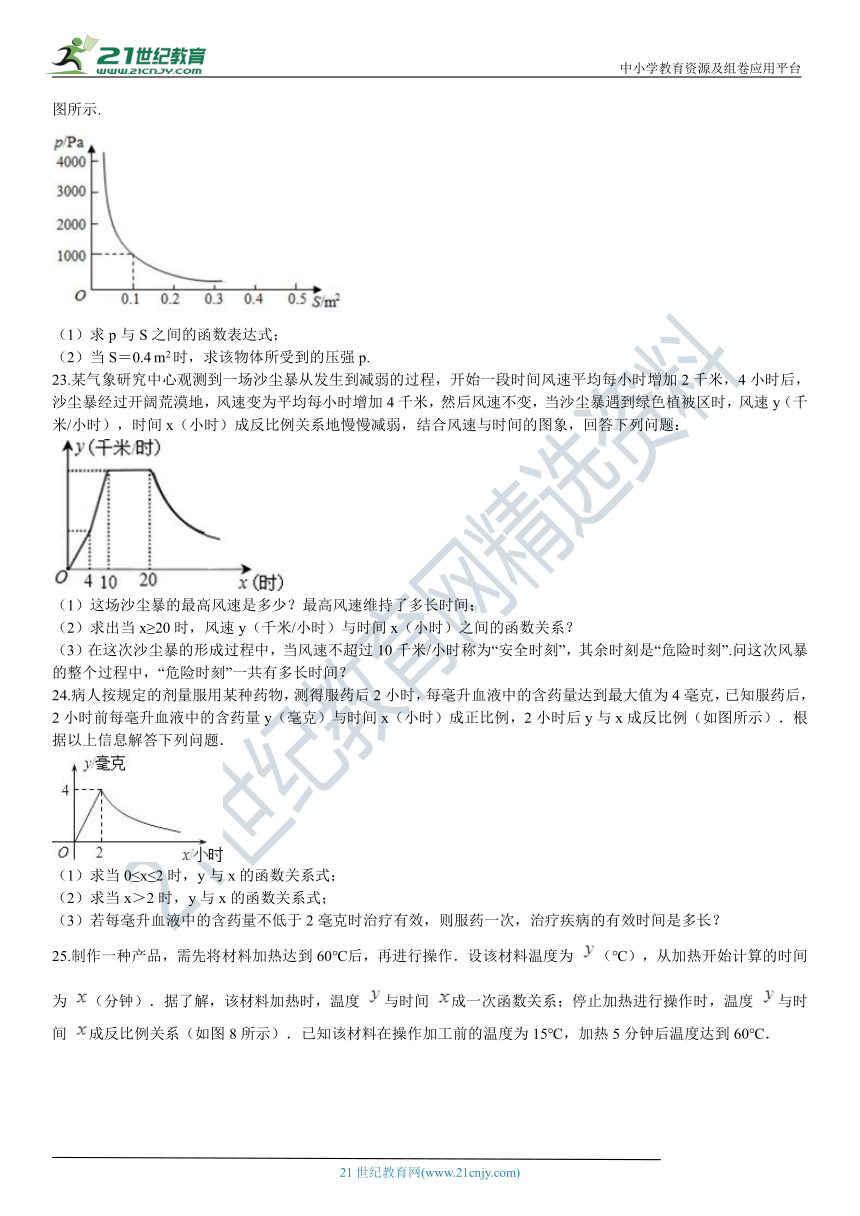
22.在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,其图象如图所示.
(1)求p与S之间的函数表达式;
(2)当S=0.4
m2时,求该物体所受到的压强p.
23.某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:
(1)这场沙尘暴的最高风速是多少?最高风速维持了多长时间;
(2)求出当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系?
(3)在这次沙尘暴的形成过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻是“危险时刻”.问这次风暴的整个过程中,“危险时刻”一共有多长时间?
24.病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
25.制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为
(℃),从加热开始计算的时间为
(分钟).据了解,该材料加热时,温度
与时间
成一次函数关系;停止加热进行操作时,温度
与时间
成反比例关系(如图8所示).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,
与
的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停
止操作,共经历了多少时间?
26.为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg
,
请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
答案解析部分
一、单选题
1.【答案】
B
解:由题意得,故选B。
2.【答案】
C
解:设函数解析式为P
,
∵当V=1.5m3时,p=16000Pa,∴k=Vp=24000,∴p
,
∵气球内的气压大于40000Pa时,气球将爆炸,∴
4000,
解得:v≥0.6,
即气球的体积应不小于0.6m3.
故答案为:C.
3.【答案】
C
解:假设反比例函数关系式为:
(其中
为常数且不为零,
为正数),
由图可知点(1,3)在反比例函数上,故将点代入函数可得:
,故
.
∵
,
∴
,
解上述不等式得:
,即时间
不小于
.
故答案为:C.
4.【答案】
D
解:∵直线y=-x+3与y轴交于点A,
∴A(0,3),即OA=3,
∵AO=3BO,
∴OB=1,
∴点C的横坐标为-1,
∵点C在直线y=-x+3上,
∴当x=-1时,y=-(-1)+3=4,
∴点C的坐标为(-1,4).
∴反比例函数的解析式为:y=
,
故答案为:D.
5.【答案】
C
解:∵点(12,18)在双曲线y=?上,
∴k=12×18=216
∴
当x=16时y=13.5.
故答案为:C.
6.【答案】
B
解:设点C(m,
),
∵直线y=﹣
x+1交y轴于点B,则OB=1,
∵△ODE的面积与△OCB的面积相等,
即
(﹣k)=
×OB×(﹣m),解得:m=k,
将点C的坐标代入一次函数表达式得:
=﹣
m+1,
解得:m=﹣2=k,
故答案为:B.
7.【答案】
B
解:AC=m-1,CQ=n,
则S四边形ACQE=AC?CQ=(m-1)n=mn-n.
∵P(1,4)、Q(m,n)在函数y=
(x>0)的图象上,
∴mn=k=4(常数).
∴S四边形ACQE=AC?CQ=4-n,
∵当m>1时,n随m的增大而减小,
∴S四边形ACQE=4-n随m的增大而增大.
故答案为:B.
8.【答案】
D
解:A、由图象可知,反比例函数图象经过(3,3),应用待定系数法可得该反比例函数关系式为
,因此,
当x=3时,y=3,点C与点M重合,即EC=EM,选项A不符合题意;
B、根据等腰直角三角形的性质,当x=3时,y=3,点C与点M重合时,EM=
,
当y=9时,
,即EC=
,所以,EC<EM,选项B不符合题意;
C、根据等腰直角三角形的性质,EC=
,CF=
,
即EC·CF=
,为定值,所以不论x如何变化,EC·CF的值不变,选项C不符合题意;
D、根据等腰直角三角形的性质,BE=x,DF=y,所以BE·DF=
,为定值,所以不论y如何变化,BE·DF的值不变,选项D符合题意.
故答案为:D.
9.【答案】
D
解:连接OA、OC、OD、OB,如图:
由反比例函数的性质可知S△AOE=S△BOF=
|k1|=
k1
,
S△COE=S△DOF=
|k2|=﹣
k2
,
∵S△AOC=S△AOE+S△COE
,
∴
?AC?OE=
×2OE=OE=
(k1﹣k2)…①,∵S△BOD=S△DOF+S△BOF
,
∴
?BD?OF=
×(EF﹣OE)=
×(3﹣OE)=
﹣
OE=
(k1﹣k2)…②,由①②两式解得OE=1,则
=2.故答案为:D.
10.【答案】
C
解:对于直线
,令x=0,得到y=2;令y=0,得到x=1,∴A(1,0),B(0,﹣2),即OA=1,OB=2,在△OBA和△CDA中,∵∠AOB=∠ADC=90°,∠OAB=∠DAC,OA=AD,∴△OBA≌△CDA(AAS),∴CD=OB=2,OA=AD=1,∴
(同底等高三角形面积相等),选项①符合题意;
∴C(2,2),把C坐标代入反比例解析式得:k=4,即
,由函数图象得:当0<x<2时,
,选项②不符合题意;
当x=3时,
,
,即EF=
=
,选项③符合题意;
当x>0时,
随x的增大而增大,
随x的增大而减小,选项④符合题意,
故答案为:C.
二、填空题
11.【答案】400
解:∵一定质量的气体的压强P与它的体积V成反比例,当V=200时,P=50,
∴K=PV=1000,
∴当P=25时,V=1000÷25=400.
故答案为:400.
12.【答案】
y=
解:容积300m3,原有水100m3
,
还需注水200m3
,
由题意得:?y=??.
13.【答案】
300
解:设需要的力大小为x,
由题意得:900×0.5=x×1.5,
解得:x=300.
故答案为:300.
14.【答案】
解:如图,
一次函数y1=k1x
(k1≠0)与反比例函数y2=(k2≠0)图象相交于点M、N,
∴M、N点关于原点对称,
∴N
(3,
-2)
,
把M
(-3,
2)代入y1=k1x得
-3k1=2,解得k1=-
,
∴一次函数解析式为y1=-x,
当y=5时,-x=5,解得x=-
,
∴若y2故答案为:-15.【答案】
或
解:由题可得
,
可得
,
根据△ABC是等腰直角三角形可得:
,
解得
,
当k=1时,点C的坐标为
,
当k=-1时,点C的坐标为
,
故答案为
或
.
16.【答案】
50
解:由图像可知两函数图像经过点(10,6),
设药物燃烧后y与x的函数解析式为y=
,
k=10×6=60;
∴y=;
∵当y=1.2时,y=.
故答案为:50
三、综合题
17.【答案】
(1)解:由题意可得:100=vt
则v=
(2)解:∵不超过5小时卸完船上的这批货物,
∴t≤5,
则v≥
=20,
答:平均每小时至少要卸货20吨。
18.【答案】
(1)解:设轮船上的货物总量为k吨,根据已知条件得k=30×8=240,所以v关于t的函数表达式为v=
(2)解:∵v=
,
∴t=
,
∵t≤5,
∴
≤5,
解得v≥48.
即平均每天至少要卸货48吨
19.【答案】
(1)解:由题意得
,所以y关于x的函数表达式为
的取值范围为
.
(2)解:∵
,
∴在第一象限内,y随x的增大而减小,且
,
∴当
时,y有最大值是12.∴高线长有最大值为12cm.
20.【答案】
(1)240
(2)解:设y与x的函数表达式为
.
∵当
时,
.
∴
,
∴
,
∴
,
当
时,
.
(3)解:把
代入
,得:
,解得:
.
根据反比例函数的性质,y随x的增大而减小,所以为了能在
内完成任务,至少需要40人参加植树.
21.【答案】
(1)解:由题意可设p=
(k≠0)
∵V=0.8m?时,
p=112.5kPa
∴k=0.8×112.5=90
∴p=
(2)解:当1.2≤V≤1.8时
∵k=90>0
∴
?
∴50≤p≤75
(3)解:(3)气球会爆炸
由题意可知p≤150
∴
≤150
∴V≥0.6
∵0.55<0.6
∴若气球内气体的体积为0.55m?,气球会爆炸。
22.【答案】
(1)解:设p与S之间的函数表达式为p=
.
图象经过点(0.1,1000),
把S=0.1,p=1000代入p=
,得1000=
.
解得k=100.
表达式为p=
.
(2)解:当S=0.4
m2时,p=
=250(Pa).
答:当S=0.4
m2时,该物体所受到的压强p为250
Pa.
23.【答案】
(1)解:0~4时,风速平均每小时增加2千米,所以4时风速为8千米/时;
4~10时,风速变为平均每小时增加4千米,10时达到最高风速,为8+6×4=32千米/时,
10~20时,风速不变,最高风速维持时间为20﹣10=10小时;
答:这场沙尘暴的最高风速是32千米/时,最高风速维持了10小时
(2)解:设y=
,
将(20,32)代入,得32=
,
解得k=640.
所以当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系为y=
(3)解:∵4时风速为8千米/时,而4小时后,风速变为平均每小时增加4千米,
∴4.5时风速为10千米/时,
将y=10代入y=
,
得10=
,
解得x=64,
64﹣4.5=59.5(小时).
故沙尘暴的风速从开始形成过程中的10千米/小时到最后减弱过程中的10千米/小时,共经过59.5小时.
答:这次风暴的整个过程中,“危险时刻”一共经过59.5小时.
24.【答案】
(1)解:根据图象,正比例函数图象经过点(2,4),
设函数解析式为y=kx,
则2k=4,
解得k=2,
所以函数关系为y=2x(0≤x≤2)
(2)解:根据图象,反比例函数图象经过点(2,4),
设函数解析式为y=
,
则
=4,
解得k=8,
所以,函数关系为y=
(x>2)
(3)解:当y=2时,2x=2,解得x=1,
=2,解得x=4,
4﹣1=3小时,
∴服药一次,治疗疾病的有效时间是3小时
25.【答案】
(1)解:材料加热时,设
,
由题意,有
,解得
.
材料加热时,
与
的函数关系式为:
.
停止加热时,设
,由题意,有
,解得
.
停止加热进行操作时
与
的函数关系式为:
(2)解:把
代入
,得
.20+5=25(分钟)
答:从开始加热到停止操作,共经历了25分钟
26.【答案】
(1)解:设药物燃烧时y关于x的函数关系式为y=k1x(k1>0)代入(8,6)为6=8k1
∴k1=
?
设药物燃烧后y关于x的函数关系式为y=
(k2>0)代入(8,6)为6=
,
∴k2=48
∴药物燃烧时y关于x的函数关系式为
(0≤x≤8)药物燃烧后y关于x的函数关系式为
(x>8)
∴
?
(2)解:结合实际,令
中y≤1.6得x≥30
即从消毒开始,至少需要30分钟后生才能进入教室
(3)解:把y=3代入
,得:x=4
把y=3代入
,得:x=16
∵16﹣4=12
所以这次消毒是有效的
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
初中数学苏科版八年级下册11.3
用反比例函数解决问题
同步训练
一、单选题(本题共10题,每题3分,共30分)
1.一定质量的二氧化碳,当它的体积V=5,密度p=1.98kg/时,p与V
之间的函数关系式是(
?
?
?
)
A.?p=9.9V????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
2.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.?不小于0.5m3???????????????????B.?不大于0.5m3???????????????????C.?不小于0.6m3???????????????????D.?不大于0.6m3
3.如图,曲线表示温度T(℃)与时间t(h)之间的函数关系,它是一个反比例函数的图象的一支.当温度T≤2℃时,时间t应(??
)
A.?不小于
h??????????????????????B.?不大于
h??????????????????????C.?不小于
h??????????????????????D.?不大于
h
4.如图,直线y=-x+3与y轴交于点A,与反比例函数y=
(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为(??
)
A.?y=
???????????????????????????????B.?y=-
???????????????????????????????C.?y=
???????????????????????????????D.?y=-
5.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18°C的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(°C)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
(k≠0)的一部分,则当x=16时,大棚内的温度为(???
)
A.?18℃??????????????????????????????????B.?15.5℃??????????????????????????????????C.?13.5℃??????????????????????????????????D.?12℃
6.如图,在平面直角坐标系中,直线y=﹣
x+1分别交x轴,y轴于点A,B,交反比例函数y1=
(k<0,x<0),y2=
(k<0,x>0)于点C,D两点,连接OC,OD,过点D作DE⊥x轴于点E,若△ODE的面积与△OCB的面积相等,则k的值是(??
)
A.?﹣4???????????????????????????????????B.?﹣2???????????????????????????????????C.?﹣2
???????????????????????????????????D.?﹣
7.如图,在平面直角坐标系中,点
、
在函数
的图象上.当
时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D
.
QD交PA于点E
.
随着m的增大,四边形ACQE的面积(??
)
A.?减小???????????????????????????B.?增大???????????????????????????C.?先减小后增大???????????????????????????D.?先增大后减小
8.图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是(??
)
A.?当x=3时,EC<EM????????????????????????????????????????????B.?当y=9时,EC>EM
C.?当x增大时,EC·CF的值增大。?????????????????????????????D.?当y增大时,BE·DF的值不变。
9.如图,A,B两点在反比例函数
的图象上,C,D两点在反比例函数
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的值是(??
)
A.?6???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
10.如图,在直角坐标系中,直线
与坐标轴交于A、B两点,与双曲线
(
)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①
;②当0<x<3时,
;③如图,当x=3时,EF=
;④当x>0时,
随x的增大而增大,
随x的增大而减小.其中符合题意结论的个数是(
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题(本题共6题,每题2分,共12分)
11.在温度不变的条件下,一定质量的气体的压强P与它的体积V成反比例,当V=200时,P=50,则当P=25时,V=________.
12.某水池容积为300m3
,
原有水100m3
,
现以xm3/min的速度匀速向水池中注水,注满水需要y
min,则y关于x的函数表达式为________.
13.小刚欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为900牛顿和0.5米,则当动力臂为1.5米时,撬动石头需要的力大于________牛顿.(提示根据杠杆原理:阻力x阻力臂=动力x动力臂)
14.一次函数y1=k1x(k1≠0)与反比例函数y2=
(k2≠0)的图象的一个交点是M(-3,2),若y2
15.已知直线
与反比例函数
的图象交于A、B两点,当线段AB的长最小时,以AB为斜边作等腰直角三角形△ABC,则点C的坐标是________.
16.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为6mg.研究表明当每立方米空气中含药量低于1.2mg时,对人体方能无毒害作用,那么从消毒开始,至少需要经过________分钟后,学生才能回到教室.
三、综合题(本题共10题,共88分)
17.已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为ν(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时)
(1)求v关于t的函数表达式
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
18.码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地开始卸货,平均卸货速度v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上货物不超过5天卸货完毕,那么平均每天至少要缷货多少吨?
19.记面积为
的平行四边形的一条边长为x(cm),这条边上的高线长为y(cm).
(1)求y关于x的函数表达式,以及自变量x的取值范围.
(2)求当边长满足
时,高线长的最大值.
20.某校绿色行动小组组织一批人参加植树活动,完成任务的时间y(h)是参加植树人数
(人)的反比例函数,且当
人时,
.
(1)若平均每人每小时植树4棵,则这次共计要植树________棵;
(2)当
时,求y的值;
(3)为了能在
内完成任务,至少需要多少人参加植树?
21.某气球内充满一定质量的气体,当温度不变时,气球内气体的压强p(kPa)与气体的体积v(m?)成反比例。当气体的体积V=0.8m3时,气球内气体的压强p=112.5kPa。当气球内气体的压强大于150kPa时,气球就会爆炸。
(1)求p关于V的函数表达式。
(2)当气球内气体的体积从1.2m?增加至1.8
m?
(含1.2
m?和1.8m?)时,求气体压强的范围。
(3)若气球内气体的体积为0.55m?,气球会不会爆炸?请说明理由。
22.在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,其图象如图所示.
(1)求p与S之间的函数表达式;
(2)当S=0.4
m2时,求该物体所受到的压强p.
23.某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:
(1)这场沙尘暴的最高风速是多少?最高风速维持了多长时间;
(2)求出当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系?
(3)在这次沙尘暴的形成过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻是“危险时刻”.问这次风暴的整个过程中,“危险时刻”一共有多长时间?
24.病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
25.制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为
(℃),从加热开始计算的时间为
(分钟).据了解,该材料加热时,温度
与时间
成一次函数关系;停止加热进行操作时,温度
与时间
成反比例关系(如图8所示).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,
与
的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停
止操作,共经历了多少时间?
26.为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg
,
请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
答案解析部分
一、单选题
1.【答案】
B
解:由题意得,故选B。
2.【答案】
C
解:设函数解析式为P
,
∵当V=1.5m3时,p=16000Pa,∴k=Vp=24000,∴p
,
∵气球内的气压大于40000Pa时,气球将爆炸,∴
4000,
解得:v≥0.6,
即气球的体积应不小于0.6m3.
故答案为:C.
3.【答案】
C
解:假设反比例函数关系式为:
(其中
为常数且不为零,
为正数),
由图可知点(1,3)在反比例函数上,故将点代入函数可得:
,故
.
∵
,
∴
,
解上述不等式得:
,即时间
不小于
.
故答案为:C.
4.【答案】
D
解:∵直线y=-x+3与y轴交于点A,
∴A(0,3),即OA=3,
∵AO=3BO,
∴OB=1,
∴点C的横坐标为-1,
∵点C在直线y=-x+3上,
∴当x=-1时,y=-(-1)+3=4,
∴点C的坐标为(-1,4).
∴反比例函数的解析式为:y=
,
故答案为:D.
5.【答案】
C
解:∵点(12,18)在双曲线y=?上,
∴k=12×18=216
∴
当x=16时y=13.5.
故答案为:C.
6.【答案】
B
解:设点C(m,
),
∵直线y=﹣
x+1交y轴于点B,则OB=1,
∵△ODE的面积与△OCB的面积相等,
即
(﹣k)=
×OB×(﹣m),解得:m=k,
将点C的坐标代入一次函数表达式得:
=﹣
m+1,
解得:m=﹣2=k,
故答案为:B.
7.【答案】
B
解:AC=m-1,CQ=n,
则S四边形ACQE=AC?CQ=(m-1)n=mn-n.
∵P(1,4)、Q(m,n)在函数y=
(x>0)的图象上,
∴mn=k=4(常数).
∴S四边形ACQE=AC?CQ=4-n,
∵当m>1时,n随m的增大而减小,
∴S四边形ACQE=4-n随m的增大而增大.
故答案为:B.
8.【答案】
D
解:A、由图象可知,反比例函数图象经过(3,3),应用待定系数法可得该反比例函数关系式为
,因此,
当x=3时,y=3,点C与点M重合,即EC=EM,选项A不符合题意;
B、根据等腰直角三角形的性质,当x=3时,y=3,点C与点M重合时,EM=
,
当y=9时,
,即EC=
,所以,EC<EM,选项B不符合题意;
C、根据等腰直角三角形的性质,EC=
,CF=
,
即EC·CF=
,为定值,所以不论x如何变化,EC·CF的值不变,选项C不符合题意;
D、根据等腰直角三角形的性质,BE=x,DF=y,所以BE·DF=
,为定值,所以不论y如何变化,BE·DF的值不变,选项D符合题意.
故答案为:D.
9.【答案】
D
解:连接OA、OC、OD、OB,如图:
由反比例函数的性质可知S△AOE=S△BOF=
|k1|=
k1
,
S△COE=S△DOF=
|k2|=﹣
k2
,
∵S△AOC=S△AOE+S△COE
,
∴
?AC?OE=
×2OE=OE=
(k1﹣k2)…①,∵S△BOD=S△DOF+S△BOF
,
∴
?BD?OF=
×(EF﹣OE)=
×(3﹣OE)=
﹣
OE=
(k1﹣k2)…②,由①②两式解得OE=1,则
=2.故答案为:D.
10.【答案】
C
解:对于直线
,令x=0,得到y=2;令y=0,得到x=1,∴A(1,0),B(0,﹣2),即OA=1,OB=2,在△OBA和△CDA中,∵∠AOB=∠ADC=90°,∠OAB=∠DAC,OA=AD,∴△OBA≌△CDA(AAS),∴CD=OB=2,OA=AD=1,∴
(同底等高三角形面积相等),选项①符合题意;
∴C(2,2),把C坐标代入反比例解析式得:k=4,即
,由函数图象得:当0<x<2时,
,选项②不符合题意;
当x=3时,
,
,即EF=
=
,选项③符合题意;
当x>0时,
随x的增大而增大,
随x的增大而减小,选项④符合题意,
故答案为:C.
二、填空题
11.【答案】400
解:∵一定质量的气体的压强P与它的体积V成反比例,当V=200时,P=50,
∴K=PV=1000,
∴当P=25时,V=1000÷25=400.
故答案为:400.
12.【答案】
y=
解:容积300m3,原有水100m3
,
还需注水200m3
,
由题意得:?y=??.
13.【答案】
300
解:设需要的力大小为x,
由题意得:900×0.5=x×1.5,
解得:x=300.
故答案为:300.
14.【答案】
一次函数y1=k1x
(k1≠0)与反比例函数y2=(k2≠0)图象相交于点M、N,
∴M、N点关于原点对称,
∴N
(3,
-2)
,
把M
(-3,
2)代入y1=k1x得
-3k1=2,解得k1=-
,
∴一次函数解析式为y1=-x,
当y=5时,-x=5,解得x=-
,
∴若y2
或
解:由题可得
,
可得
,
根据△ABC是等腰直角三角形可得:
,
解得
,
当k=1时,点C的坐标为
,
当k=-1时,点C的坐标为
,
故答案为
或
.
16.【答案】
50
解:由图像可知两函数图像经过点(10,6),
设药物燃烧后y与x的函数解析式为y=
,
k=10×6=60;
∴y=;
∵当y=1.2时,y=.
故答案为:50
三、综合题
17.【答案】
(1)解:由题意可得:100=vt
则v=
(2)解:∵不超过5小时卸完船上的这批货物,
∴t≤5,
则v≥
=20,
答:平均每小时至少要卸货20吨。
18.【答案】
(1)解:设轮船上的货物总量为k吨,根据已知条件得k=30×8=240,所以v关于t的函数表达式为v=
(2)解:∵v=
,
∴t=
,
∵t≤5,
∴
≤5,
解得v≥48.
即平均每天至少要卸货48吨
19.【答案】
(1)解:由题意得
,所以y关于x的函数表达式为
的取值范围为
.
(2)解:∵
,
∴在第一象限内,y随x的增大而减小,且
,
∴当
时,y有最大值是12.∴高线长有最大值为12cm.
20.【答案】
(1)240
(2)解:设y与x的函数表达式为
.
∵当
时,
.
∴
,
∴
,
∴
,
当
时,
.
(3)解:把
代入
,得:
,解得:
.
根据反比例函数的性质,y随x的增大而减小,所以为了能在
内完成任务,至少需要40人参加植树.
21.【答案】
(1)解:由题意可设p=
(k≠0)
∵V=0.8m?时,
p=112.5kPa
∴k=0.8×112.5=90
∴p=
(2)解:当1.2≤V≤1.8时
∵k=90>0
∴
?
∴50≤p≤75
(3)解:(3)气球会爆炸
由题意可知p≤150
∴
≤150
∴V≥0.6
∵0.55<0.6
∴若气球内气体的体积为0.55m?,气球会爆炸。
22.【答案】
(1)解:设p与S之间的函数表达式为p=
.
图象经过点(0.1,1000),
把S=0.1,p=1000代入p=
,得1000=
.
解得k=100.
表达式为p=
.
(2)解:当S=0.4
m2时,p=
=250(Pa).
答:当S=0.4
m2时,该物体所受到的压强p为250
Pa.
23.【答案】
(1)解:0~4时,风速平均每小时增加2千米,所以4时风速为8千米/时;
4~10时,风速变为平均每小时增加4千米,10时达到最高风速,为8+6×4=32千米/时,
10~20时,风速不变,最高风速维持时间为20﹣10=10小时;
答:这场沙尘暴的最高风速是32千米/时,最高风速维持了10小时
(2)解:设y=
,
将(20,32)代入,得32=
,
解得k=640.
所以当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系为y=
(3)解:∵4时风速为8千米/时,而4小时后,风速变为平均每小时增加4千米,
∴4.5时风速为10千米/时,
将y=10代入y=
,
得10=
,
解得x=64,
64﹣4.5=59.5(小时).
故沙尘暴的风速从开始形成过程中的10千米/小时到最后减弱过程中的10千米/小时,共经过59.5小时.
答:这次风暴的整个过程中,“危险时刻”一共经过59.5小时.
24.【答案】
(1)解:根据图象,正比例函数图象经过点(2,4),
设函数解析式为y=kx,
则2k=4,
解得k=2,
所以函数关系为y=2x(0≤x≤2)
(2)解:根据图象,反比例函数图象经过点(2,4),
设函数解析式为y=
,
则
=4,
解得k=8,
所以,函数关系为y=
(x>2)
(3)解:当y=2时,2x=2,解得x=1,
=2,解得x=4,
4﹣1=3小时,
∴服药一次,治疗疾病的有效时间是3小时
25.【答案】
(1)解:材料加热时,设
,
由题意,有
,解得
.
材料加热时,
与
的函数关系式为:
.
停止加热时,设
,由题意,有
,解得
.
停止加热进行操作时
与
的函数关系式为:
(2)解:把
代入
,得
.20+5=25(分钟)
答:从开始加热到停止操作,共经历了25分钟
26.【答案】
(1)解:设药物燃烧时y关于x的函数关系式为y=k1x(k1>0)代入(8,6)为6=8k1
∴k1=
?
设药物燃烧后y关于x的函数关系式为y=
(k2>0)代入(8,6)为6=
,
∴k2=48
∴药物燃烧时y关于x的函数关系式为
(0≤x≤8)药物燃烧后y关于x的函数关系式为
(x>8)
∴
?
(2)解:结合实际,令
中y≤1.6得x≥30
即从消毒开始,至少需要30分钟后生才能进入教室
(3)解:把y=3代入
,得:x=4
把y=3代入
,得:x=16
∵16﹣4=12
所以这次消毒是有效的
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
