12.2 证明 同步训练（含解析）

中小学教育资源及组卷应用平台
初中数学苏科版七年级下册12.2
证明
同步训练
一、单选题（本题共10题，每题3分，共30分）
1.下列运用等式性质进行的变形中，正确的是（??
）
A.?若a＝b，则ac＝bc?????????????????????????????????????????????B.?若x＝y，则5﹣x＝5+y
C.?若2x＝3，则x＝
?????????????????????????????????????????????D.?若a＝b，则
＝
2.如图，下列判断正确的是（??
）
A.?若∠1=∠2，则AD∥BC????????????????????????????????????????B.?若∠1=∠2，则AB∥CD
C.?若∠A=∠3，则AD∥BC????????????????????????????????????????D.?若∠3+∠ADC=180°
，则AB∥CD
3.如图，在
中，
是
延长线上点，
，
，则
等于（??
）
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
4.如图，点
在
的延长线上，下列条件不能判断
的是（
??）
A.???????????????????B.?
??????????????????C.?∠5=∠B??????????????????D.?
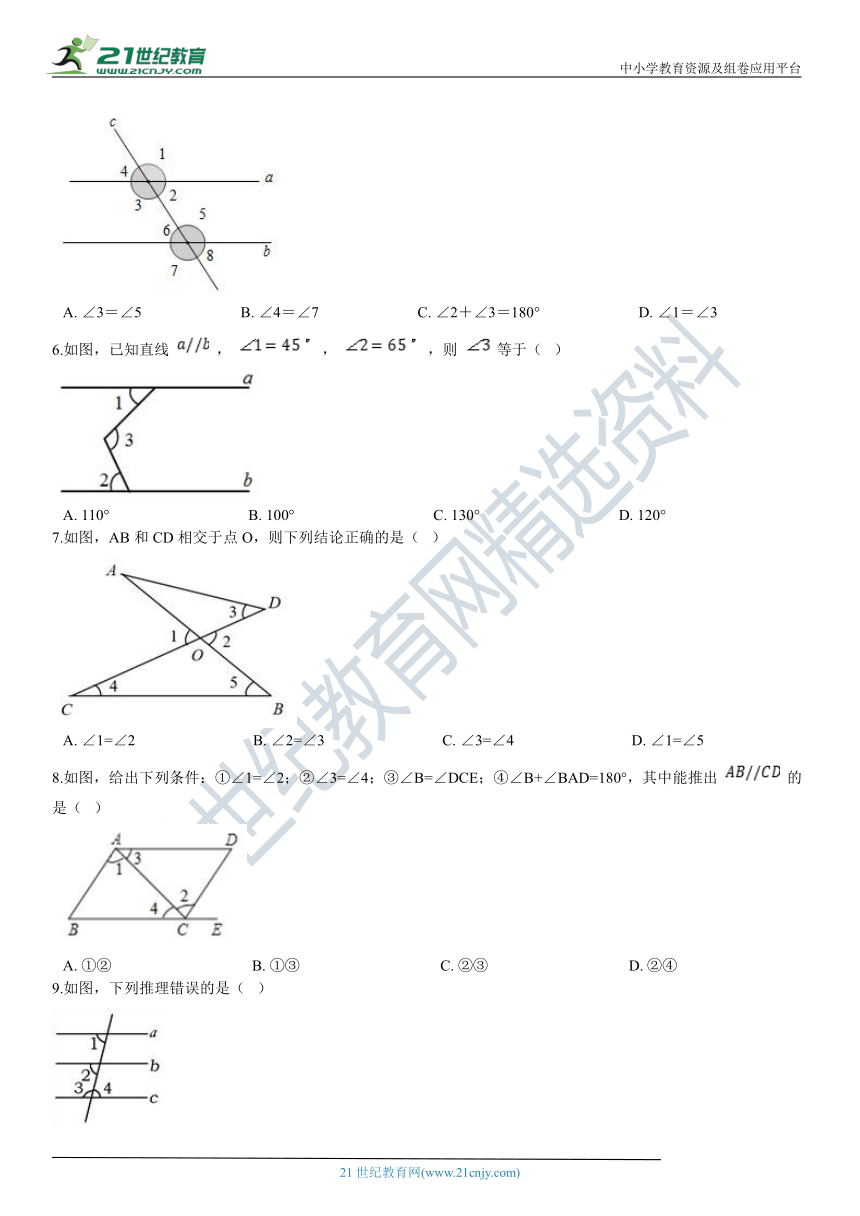
5.如图，直线a，b被直线c所截，下列条件能判断a∥b的是（?
）
A.?∠3＝∠5??????????????????????????B.?∠4＝∠7??????????????????????????C.?∠2＋∠3＝180°??????????????????????????D.?∠1＝∠3
6.如图，已知直线
，
，
，则
等于（?
）
A.?110°????????????????????????????????????B.?100°????????????????????????????????????C.?130°????????????????????????????????????D.?120°
7.如图，AB和CD相交于点O，则下列结论正确的是（?
）
A.?∠1=∠2???????????????????????????????B.?∠2=∠3???????????????????????????????C.?∠3=∠4???????????????????????????????D.?∠1=∠5
8.如图，给出下列条件：①∠1=∠2；②∠3=∠4；③∠B=∠DCE；④∠B+∠BAD=180°，其中能推出
的是（?
）
A.?①②?????????????????????????????????????B.?①③?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
9.如图，下列推理错误的是（?
）
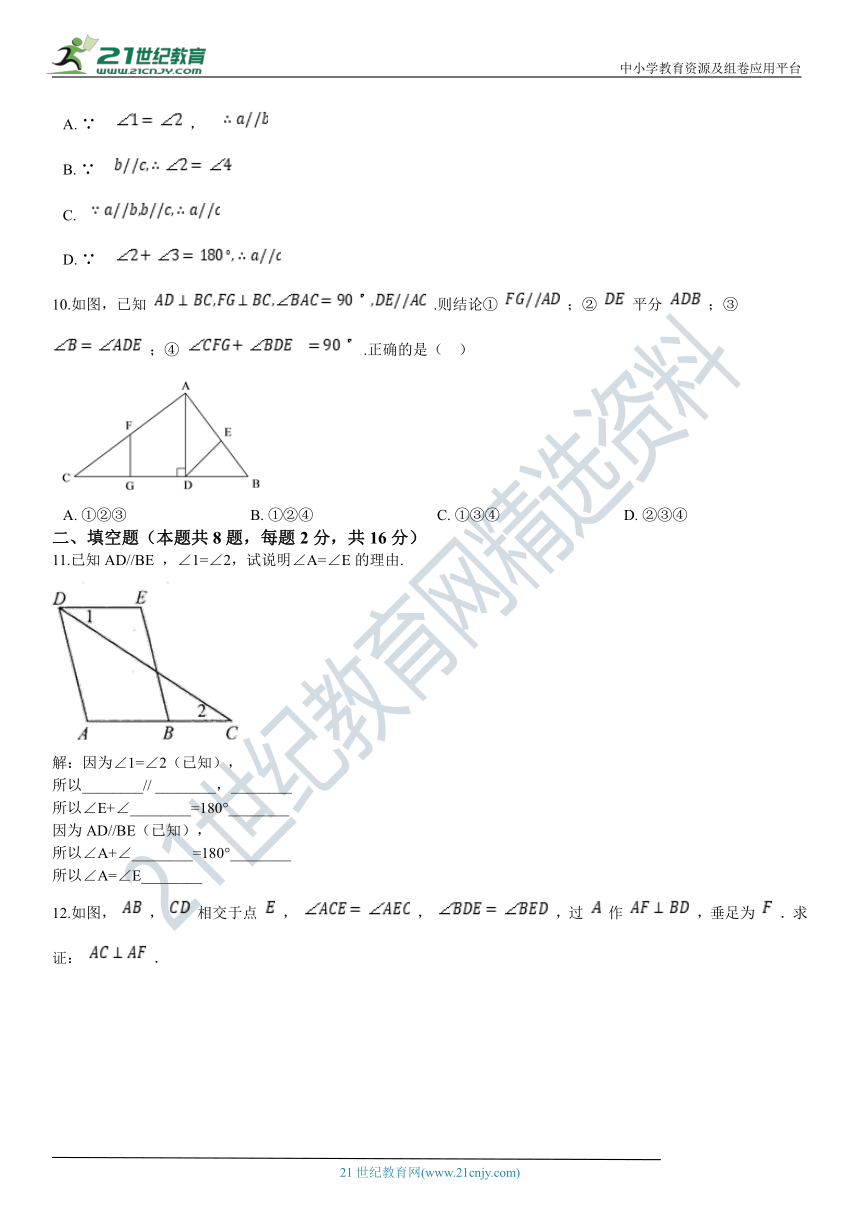
A.?∵
，
B.?∵
C.?
D.?∵
10.如图，已知
.则结论①
；②
平分
；③
；④
.正确的是（??
）
A.?①②③????????????????????????????????B.?①②④????????????????????????????????C.?①③④????????????????????????????????D.?②③④
二、填空题（本题共8题，每题2分，共16分）
11.已知AD//BE
，∠1=∠2，试说明∠A=∠E的理由.
解：因为∠1=∠2（已知），
所以________//
________，________
所以∠E+∠________=180°________
因为AD//BE（已知），
所以∠A+∠________=180°________
所以∠A=∠E________
12.如图，
，
相交于点
，
，
，过
作
，垂足为
．求证：
．
证明：∵
，
又
（________）
∴
∴
（________）
∴
（________）
∵
∴
（________）
∴
∴
13.如图，已知CD⊥DA，DA⊥AB，∠1=∠4.试说明DF∥AE.请你完成下列填空，把证明过程补充完整.
证明：∵________（________）
∴∠CDA=90°，∠DAB=90°（________）.
∴∠4+∠3=90°，∠2+∠1=90°.
又∵∠1=∠4，
∴________（________），
∴DF∥AE（________）.
14.推理填空，如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．
解：∵∠A=∠F（________），
∴AC∥DF（________），
∴∠D=∠1（________），
又∵∠C=∠D（________），
∴∠1=∠C（________），
∴BD∥CE（________）．
15.已知：如图，在△
中，
于点D，E是
上一点，且
．求证：
．
请在括号内填写出证明依据．
证明：∵
（已知）
∴
（________）
∵
（________）
∴
（________）
∴
∥
（________）
∴
（________）
16.填写推理理由，将过程补充完整：
如图，
，
试说明
解：
，
?________（________），
，
（等量代换），
，
，即
，
?________（等量代换），
（________）．
17.补全解答过程：
如图，∠1+∠2＝180°，∠3＝∠A
．
求证：∠B＝∠C
．
证明：∵∠1+∠2＝180°，
∴________（同旁内角互补，两直线平行）．
∴∠3＝∠D（________）．
又∵∠3＝∠A
，
∴________．
∴AB∥CD（________）．
∴∠B＝∠C（________）．
18.完成下面的证明：
（1）已知：如图，AB∥CD
求证：∠1+∠3
=
180°
证明：∵
AB∥CD（已知），
∴
∠1+∠2
=
180°（________）
又∵
∠2
=?
∠3（________）
∴
∠1+∠3=180°（________）
（2）已知：如图，AM∥EF
，
∠1
=
∠B
．
求证：∠2
=
∠C
．
证明：∵
∠1
=?
∠B（已知），
∴
EF∥BC（________）
∵
AM∥EF（已知），
∴
AM∥BC（________）
∴
∠2
=?
∠C（________）
三、解答题（本题共8题，共84分）
19.如图，已知∠1=∠2，∠C=∠F.请指出∠A与∠D
的数量关系，并说明理由.
20.如图，E点为DF上的点，B为AC上的点，∠1＝∠2，∠C＝∠D.
试说明：AC∥DF.
21.已知：如图，∠1=∠2，∠3=∠E，证明：∠A=∠EBC.
22.完善下列证明过程，已知：如图，已知∠DAF=∠F，∠B=∠D.证明：AB∥DC
证明：∵∠DAF=∠F
(???
▲???
)
∴???
▲???
∥???
▲???
（???
▲???
）
∴∠D=∠DCF
(???
▲???
)
∵∠B=∠D（???
▲???
）
∴∠???
▲???
=∠DCF
(等量代换)
∴AB∥DC
(???
▲???
)
23.已知：如图，在△ABC中CD交AB边于点D，直线DE平分
且与直线BE相交于点E，
，
.
求证：
证明：理由如下：
平分
（已知）
（已知）
（等量代换）
又
（已知）
（等量代换）
24.如图，已知
，∠B=∠D，AE交BC的延长线于点E.
（1）求证：
；
（2）若∠1=∠2=60°，∠BAC=2∠EAC，求∠DCE的度数.
25.已知：直线
分别与直线
，
交于点
，
．
平分
，
平分
，并且
．
（1）如图1，求证：
；
（2）如图2，
，在不添加任何辅助线的情况下，请直接写出图2中四个角，使写出的每个角的度数都为
．
26.如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F.
（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为________.
（2）当△PMN所放位置如图②所示时，PN交CD于点H.请猜想∠PFD与∠AEM的数量关系并证明.
（3）在（2）的条件下，若MN与CD交于点O，且∠DON＝20°，∠PEB＝15°，求∠N的度数.
答案解析部分
一、单选题
1.【答案】
A
解：A、若a＝b，则ac＝bc?，正确；
B、
若x＝y，则5+x＝5+y?，错误；
C、
若2x＝3，则x=?，错误；
D、
若a＝b，则??＝?
（c≠0）；
故答案为：A.
2.【答案】
B
解：AB、若∠1=∠2，则AB∥CD，则A错误，B正确；
C、若∠A=∠3，无法判断平行，错误；
D、若∠3+∠ADC=180°
，无法判断平行，错误；
故答案为：B.
3.【答案】
D
解：∵
，
，
∴∠A=120°-40°=80°.
故答案为：D.
4.【答案】
B
解：A．由
，得
（内错角相等，两直线平行），故该选项不符合题意．
B．由
，得
（内错角相等，两直线平行），并不能证明
，故该选项符合题意．
C．由∠5=∠B，得
（同位角相等，两直线平行），故该选项不符合题意．
D．由
，得
（同旁内角互补，两直线平行），故该选项不符合题意．
故答案为：B．
5.【答案】
A
解：A选项，
∵∠3＝∠5（已知），
∴a∥b（内错角相等，两直线平行）.
B选项，∠4＝∠7，∠4与∠7无关系，不能判定平行；
C选项，∠2＋∠3＝180°，∠2与∠3为邻补角，不能判定平行；
D选项，∠1＝∠3，∠1与∠3为对顶角，不能判定两直线平行；
故答案为：A.
6.【答案】
A
解：如图，作直线c//
，
直线
，直线c//
，
c//
，
（两直线平行，内错角相等）
（两直线平行，内错角相等）
（等量代换）
故答案为：A.
7.【答案】
A
解：A、∠1、∠2互为对顶角，对顶角相等，故A符合题意；
B、根据三角形外角定理，∠2=∠3+∠A，∠2>∠3，故不符合题意；
C、根据三角形外角定理，∠1=∠4+∠5，∠2=∠3+∠A，∠3和∠4不一定相等，故不符合题意；
D、根据三角形外角定理，∠1=∠5+∠4，∠1>∠5，故不符合题意；
故答案为：A．
8.【答案】
B
解：①∵∠1=∠2，
∴AB∥CD；
②∵∠3=∠4，
∴AD∥BC；
③∵∠B=∠DCE，
∴AB∥CD；
④∵∠B+∠BAD=180°，
∴AD∥BC；
∴能得到AB∥CD的条件是①③.
故答案为：B
9.【答案】
D
解：A.
∵
，
，不符合题意；?
B.
∵
，不符合题意；
C.
，不符合题意；
D.
∵
∴
，故D符合题意；
故答案为：D.
10.【答案】
C
解：∵
∴∠FGB=∠ADB=90°，
∴FG∥AD，∠ADE+∠BDE=90°，
故①正确；
∵DE∥AC，
∴∠DEB=∠CAB=90°，
∴∠B+∠BDE=90°，
∴
，
∴③正确；
∵
，
∴∠BDE=∠C，
∵∠FGC=90°，
∴∠C+∠CFG=90°，
∴∠BDE+∠CFG=90°，
∴④正确；
∵∠ADB=90°，
∴∠ADE+∠BDE=90°，
∴②不正确；
故答案为：C.
二、填空题
11.【答案】
DE；AC；A内错角相等，两直线平行；ABE；两直线平行，同旁内角互补；ABE；两直线平行，同旁内角互补；等量代换
解：因为∠1=∠2（已知），
所以DE∥AC（内错角相等，两直线平行），
所以∠E+∠ABE=180°（两直线平行，同旁内角互补），
因为AD//BE（已知），
所以∠A+∠ABE=180°（两直线平行，同旁内角互补），
所以∠A=∠E（等量代换），
故答案为：DE；AC；内错角相等，两直线平行；ABE；两直线平行，同旁内角互补；ABE；两直线平行，同旁内角互补；等量代换.
12.【答案】
对顶角相等；内错角相等，两直线平行；两直线平行，内错角相等；垂直定义
解：证明：∵
，
，
又
（对顶角相等），
∴
，
∴
（内错角相等，两直线平行），
∴
（两直线平行，内错角相等），
∵
，
∴
（垂直定义），
∴
，
∴
．
故答案为：对顶角相等；内错角相等，两直线平行；两直线平行，内错角相等；垂直定义．
13.【答案】
CD⊥DA，DA⊥AB；已知；垂直定义；∠2=∠3；等角的余角相等；内错角相等，两直线平行
解：证明：如图：
∵
CD⊥DA，DA⊥AB
（已知）
?∴∠CDA=90°，∠DAB=90°
（
垂直定义
）.
?∴∠4+∠3=90°，∠2+∠1=90°.
?又∵∠1=∠4，
?∴∠2=∠3?
（
等角的余角相等?
），
?∴DF∥AE
（
内错角相等，两直线平行?
）.
故答案为：CD⊥DA，DA⊥AB
，
已知；垂直定义；∠2=∠3
，等角的余角相等；内错角相等，两直线平行.
14.【答案】
已知；内错角相等，两直线平行；两直线平行，内错角相等；已知；等量代换；同位角相等，两直线平行
解：∵∠A=∠F（已知），
?∴AC∥DF（内错角相等，两直线平行），
∴∠D=∠1（两直线平行，内错角相等），
?又∵∠C=∠D（已知），
?
∴∠1=∠C（等量代换），
∴BD∥CE（同位角相等，两直线平行）．
故答案是：已知；内错角相等，两直线平行；两直线平行，内错角相等；已知；等量代换；同位角相等，两直线平行
15.【答案】
垂直定义；已知；同角的余角相等；内错角相等，两直线平行；两直线平行，同位角相等
解：证明：∵CD⊥AB（已知），
∴∠1+∠3=90°（垂直定义），
∵∠1+∠2=90°（已知），
∴∠3=∠2（同角的余角相等），
∴DE∥BC（内错角相等，两直线平行），
∴∠AED=∠ACB（两直线平行，同位角相等）.
故答案为：垂直定义；已知；同角的余角相等；内错角相等，两直线平行；两直线平行，同位角相等．
16.【答案】
；两直线平行，同位角相等；；内错角相等，两直线平行
（内错角相等，两直线平行）
解：
，
（两直线平行，同位角相等）
，
（等量代换），
，
，即
，
（等量代换），
（内错角相等，两直线平行）．
17.【答案】
AD∥EF；两直线平行，同位角相等；∠A=∠D；内错角相等，两直线平行；两直线平行，内错角相等
解：∵∠1+∠2=180°，
∴AD∥EF（同旁内角互补，两直线平行）．
∴∠3=∠D（两直线平行，同位角相等）．
又∵∠3=∠A
，
∴∠A=∠D
．
∴AB∥CD（内错角相等，两直线平行）．
∴∠B=∠C（两直线平行，内错角相等）．
故答案为：AD∥EF；两直线平行，同位角相等；∠A=∠D；内错角相等，两直线平行；两直线平行，内错角相等．
18.【答案】
（1）两直线平行，同旁内角互补；对顶角相等；等量代换
（2）同位角相等，两直线平行；平行公理推论；两直线平行，内错角相等
解：（1）证明：∵
（已知）
∴
（两直线平行，同旁内角互补
）
又∵
（
对顶角相等
）
∴
（
等量代换
）；（2）证明：∵
（已知）
∴
（
同位角相等，两直线平行
）
∵
（已知）
∴
（
平行公理推论
）
∴
（
两直线平行，内错角相等
）．
三、解答题
19.【答案】
∠A=∠D
理由：∠A与∠D
的数量关系为∠A=∠D.
理由：∵∠2=∠AGC，∠1=∠2，
∴∠1=∠AGC，
∴BF∥CE,
∴∠F=∠DEC
∵∠C=∠F，
∴∠C=∠DEC，
∴DF∥AC，
∴∠A=∠D.
20.【答案】
证明：∵∠1=∠2，∠1=∠3，
∴∠2=∠3,
∴DB∥EC，
∴∠C=∠ABD，
∵
∠C＝∠D
,
∴∠ABD，
∵
∠ABD＝∠D
,
∴AC∥DF.
21.【答案】
证明：
∵∠1=∠2（已知），
∴DB∥EC（内错角相等，两直线平行），
∴∠E=∠4（两直线平行，内错角相等），
又∵∠E=∠3（已知），
∴∠3=∠4（
等量代换），
∴AD∥BE（内错角相等，两直线平行），
∴∠A=∠EBC（两直线平行，同位角相等），
22.【答案】
证明：∵∠DAF＝∠F（已知），
∴AD∥BF（内错角相等，两直线平行
），
∴∠D＝∠DCF（两直线平行，内错角相等），
∵∠B＝∠D（已知），
∴∠B＝∠DCF（等量代换），
∴AB∥DC（同位角相等，两直线平行）．
23.【答案】
解：
理由如下：
平分
（已知）
（已知）
（等量代换）
（同位角相等，两直线平行）
（两直线平行，内错角相等）
又
（已知）
（等量代换）
（内错角相等，两直线平行）.
24.【答案】
（1）证明：∵
，
∴
∵
，
∴
，
∴
（2）解：∵
，
，
∴
，
∴
∵
，
∴
∵
∴
25.【答案】
（1）证明：∵
，∴
．
∵
平分
，
平分
，∴
，
．
∴
．
∴
．
（2）解：由（1）知AB
CD，
∴∠AEF+∠CFE=180°，
∵∠AEF=2∠CFN=∠CFE，
∴∠AEF=∠CFE=90°，
∴∠CFN=∠EFN=∠FEM=∠BEM=45°，∠BEG=∠CFH=∠DFE=90°,
∴∠AEM=∠GEM=∠HFN=∠DFN=90°+45°=135°，
∴度数为135°的角有：
、??
、?
、??
．
答案】
（1）∠AEM+∠PFD=90°
（2）猜想：∠PFD-∠AEM=90°
证明：∵∠P=90°，∠PEB=∠AEM，∠PHE=∠BHN
∴∠PEB+∠PHE=90°
∴∠AEM+∠BHN=90°即∠BHN=90°-∠AEM
∵AB∥CD，
∴∠BHN+∠PFD=180°
∴90°-∠AEM+∠PFD=180°
∴∠PFD-∠AEM=90°.
（3）解：∵∠PEB=∠AEM=15°，∠PFD-∠AEM=90°.
∴∠PFD=∠OFN=90°+15°=105°，
∵∠N=180°-∠DON-∠OFN=180°-105°-20°=55°.
解：（1）过点P作PG∥AB，
?
∵AB∥CD
∴
AB∥CD
∥PG，
∴∠AEM=∠MPG，∠PFD=∠NPG，?
?
∵∠MPN=∠MPG+∠NPG=90°，
∴∠AEM+∠PFD=90°
故答案为：∠AEM+∠PFD=90°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)