【2020年中考数学二轮复习】专题五 几何动态探究专题(含答案)
文档属性
| 名称 | 【2020年中考数学二轮复习】专题五 几何动态探究专题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 17:44:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
几何动态探究专题
专题解读
几何动态问题是近些年来中考数学的热点题型.纵观全国各地的中考数学试卷,动态几何型综合题常常出现在一张试卷的压轴题位置,估计这一趋势在今后几年的中考中仍将持续.这类试题信息量大,综合性较强,往往涉及到函数、直线型、圆等初中数学的多个重点考查对象,对获取信息和处理信息的能力要求较高,应加大训练的力度.
解题策略:几何动态型问题就是在线段、三角形、矩形圆等一些几何图形上,设计一个或几个动点(或线或面),并对这些点(或线或面)在运动变化的过程中相伴随着的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等进行研究考查.动态型问题常常集几何、代数知识于一体,数形结合,有较强的综合性.解决动态型问题需要用运动与变化的眼光去观察和研究图形,把握动点(或线或面)运动与变化的全过程,抓住其中的等量关系和变量关系,并特别关注一些不变量、不变关系或特殊关系,“动中求静,静中求解”.
几何动态型问题有时把函数、方程、不等式联系起来,当求有关图形的变量之间关系时,常建立函数模型或不等式模型求解;当求图形之间的特殊位置关系和一些特殊的值时,通常建立方程模型去求解.
考点一 探究三角形中的动点问题
典例1 如图所示,点P,Q分别是等边△ABC边AB,BC上的动点(端点除外),点P,Q以相同的速度,同时从点A,B出发.
(1)如图1所示,连接AQ,CP.求证:△ABQ≌△CAP;
(2)如图1所示,当点P,Q分别在AB,BC边上运动时,AQ,CP相交于点M,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数;
(3)如图2所示,当点P,Q在AB,BC的延长线上运动时,直线AQ,CP相交于M,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
思路导引
(1)根据等边三角形的性质,利用SAS证明△ABQ≌△CAP即可;
(2)先判定△ABQ≌△CAP,根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=60°;(3)先判定△ABQ≌△CAP,根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=120°.
名师点拨
此题是三角形的动态综合题,主要考查了等边三角形的性质、全等三角形的判定与性质等知识的综合应用.解决问题的关键是掌握全等三角形的判定方法:两边及其夹角分别对应相等的两个三角形全等.解题时注意运用全等三角形的对应边相等、对应角相等的性质,体会在运动变化过程中蕴含着不变的量.
跟踪训练1
1.如图所示,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点PAP→B的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
2.如图所示,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D,E分别在ACBC边上运动,且始终保持AD=CE.连接DE,DF,EF(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形;
(3)若AD=5,BE=7,求AC的长.
3.如图所示,在平面直角坐标系中,△AOB的顶点O是坐标原点,点A的坐标为(4,4),点B的坐标为(6,0),动点P从O开始以每秒1个单位长度的速度沿y轴正方向运动,设运动的时间为t秒(0<t<4),过点P作PN∥x轴,分别交AO,AB于点 M,N.
(1)填空:AO的长为__________,AB的长为__________.
(2)当t=1时,求点N的坐标;
(3)请直接写出MN的长为_________(用含t的代数式表示);
(4)点E是线段MN上一动点(点E不与点M,N重合),△AOE和△ABE的面积分别表示为S1和S2,当t=时,请直接写出S1·S2(即S1与S2的积)的最大值为__________.
考点二 探究特殊四边形中的动点问题
典例2 如图所示,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1所示,若k=1,则AF与AE之间的数量关系是__________;
(2)如图2所示,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)
(3)若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.
思路导引
(1)证明△EAB≌△FAD(AAS),由全等三角形的性质得出AF=AE;
(2)证明△ABE∽△ADF,由相似三角形的性质得出,则可得出结论;
(3)①当点F在DC上时,证得△GDF∽△GBA,得出,求出AG=AF=.由△ABE∽△ADF可得出,求出AE=则可得出答案;②当点F在DC的延长线上时,同理可求出EG的长.
名师点拨
本题是相似形综合题,考查了全等三角形的判定与性质,正方形的性质,矩形的性质,相似三角形的判定与性质,勾股定理等知识,熟练掌握相似三角形的判定与性质是解题的关键.注意在动态变化过程中,蕴含着确定的数量关系.
跟踪训练2
1.如图所示,正方形ABCD的边长为4点E在AB上且BE=1,F为对角线AC上一动点,则△BFE周长的最小值为( )
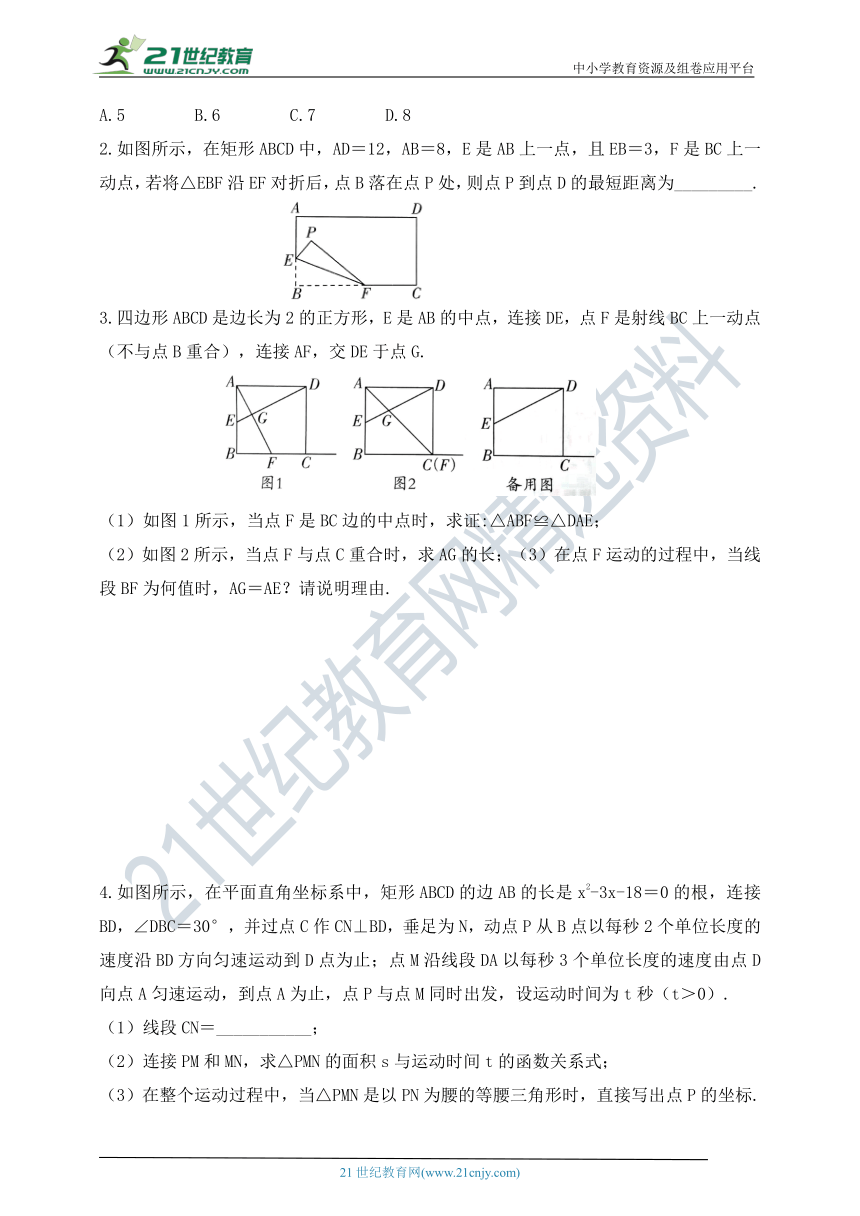
A.5 B.6 C.7 D.8
2.如图所示,在矩形ABCD中,AD=12,AB=8,E是AB上一点,且EB=3,F是BC上一动点,若将△EBF沿EF对折后,点B落在点P处,则点P到点D的最短距离为_________.
3.四边形ABCD是边长为2的正方形,E是AB的中点,连接DE,点F是射线BC上一动点(不与点B重合),连接AF,交DE于点G.
(1)如图1所示,当点F是BC边的中点时,求证:△ABF≌△DAE;
(2)如图2所示,当点F与点C重合时,求AG的长;(3)在点F运动的过程中,当线段BF为何值时,AG=AE?请说明理由.
4.如图所示,在平面直角坐标系中,矩形ABCD的边AB的长是x2-3x-18=0的根,连接BD,∠DBC=30°,并过点C作CN⊥BD,垂足为N,动点P从B点以每秒2个单位长度的速度沿BD方向匀速运动到D点为止;点M沿线段DA以每秒3个单位长度的速度由点D向点A匀速运动,到点A为止,点P与点M同时出发,设运动时间为t秒(t>0).
(1)线段CN=___________;
(2)连接PM和MN,求△PMN的面积s与运动时间t的函数关系式;
(3)在整个运动过程中,当△PMN是以PN为腰的等腰三角形时,直接写出点P的坐标.
5.如图1所示,在矩形ABCD中,AB=6,BC=8,动点P,Q分别从C点,A点同时以每秒1个单位长度的速度出发,且分别在边CA,AB上沿C→A,A→B的方向运动,当点Q运动到点B时,P,Q两点同时停止运动,设点P运动的时间为t(s),连接PQ,过点P作PE⊥PQ,PE与边BC相交于点E,连接QE.
(1)如图2所示,当t=5s时,延长EP交边AD于点F.求证:AF=CE;
(2)在(1)的条件下,试探究线段AQ,QE,CE三者之间的等量关系,并加以证明;
(3)如图3所示,当t>s时,延长EP交边AD于点F,连接FQ,若FQ平分∠AFP,求的值.
考点三 探究圆中的动点问题
典例3 古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆.”请研究如下美丽的圆.如图所示,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接 CD, PE, PC.
(1)求证:CD是⊙O的切线;
(2)小明在研究的过程中发现是一个确定的值回答这个确定的值是多少?并对小明发现的结论加以证明.
思路导引
(1)连接OD,DB,由已知可知DE垂直平分OB,则DB=DO,再由圆的半径相等,可得DB=DO=OB,即△ODB是等边三角形,则∠BDO=60°,再由等腰三角形的性质及三角形的外角性质可得∠CDB=30°,从而可得∠ODC=90°,按照切线的判定定理可得结论;
(2)连接OP,先由已知条件得OP=OB=BC=2OE,再利用两组边成比例,夹角相等来证明△OEP∽△OPC,按照相似三角形的性质得出比例式,则可得答案.
名师点拨
本题考查了切线的判定与性质及相似三角形的判定与性质,熟练掌握相关性质及定理是解题的关键.注意在动点的运动过程中存在确定的线段比值(即确定的数量关系).
跟踪训练3
1.如图所示,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连接OC,AC,当△OAC是直角三角形时,其斜边长为_________.
2.如图所示,已知直线y=-x+4与x,y轴交于AB两点,⊙O的半径为1,P为AB上一动点,PQ切⊙O于Q点.当线段PQ长取最小值时,直线PQ交y轴于M点,a为过点M的一条直线,则点P到直线a的距离的最大值为__________.
3.如图所示,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y=x-3与x轴、y轴分别交于点D,E,则△CDE面积的最小值为____________.
4.如图所示,半径为2cm的⊙O与边长为2cm的正方形ABCD的边AB相切于E,点F为正方形的中心,直线OE过F点.当正方形ABCD沿直线OF以每秒(2-)cm的速度向左运动________秒时,⊙O与正方形重叠部分的面积为()cm2.
5.如图所示,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连接CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2 cm/s的速度从A点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动,设运动时间为t(s)(0<1<2),连接EF,当t为何值时,△BEF为直角三角形.
考点四 探究函数中的动点问题
典例4 如图所示,抛物线y=-x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,
且OA=OB,点G为抛物线的顶点.
(1)求抛物线的解析式及点G的坐标;
(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的纵坐标y的取值范围.
思路导引
(1)先求出点B,点A坐标,代入解析式可求c的值,即可求解;
(2)先求出点M,点N坐标,即可求解.
名师点拨
本题考查了待定系数法求二次函数解析式,二次函数的性质,二次函数图象上点的坐标特征,熟练运用二次函数的性质是解决问题的关键.注意体会动态变化过程与函数思想的密切联系.
跟踪训练4
1.如图所示,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
2.如图所示,等腰△ABC的两个顶点A(-1,-4),B(-4,-1)在反比例函数y=(x<0)的图象上,AC=BC.过点C作边AB的垂线交反比例函数y=(x<0)的图象于点D,动点P从点D出发,沿射线CD方向运动3个单位长度,到达反比例函数y=(x>0)图象上一点,则k2=___________.
3.如图所示,在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(4,),点B在y轴的负半轴上,AB交x轴于点C,C为线段AB的中点.
(1)m=________,点C的坐标为___________;
(2)若点D为线段AB上的一个动点,过点D作DE∥y轴,交反比例函数图象于点E,求△ODE面积的最大值.
4.如图所示,已知抛物线y=ax2过点A(-3,).
(1)求抛物线的解析式;
(2)已知直线过点A,M(,0)且与抛物线交于另一点B,与y轴交于点C,求证:MC2=MA·MB;
(3)若点P,D分别是抛物线与直线l上的动点,以OC为一边且顶点为O,C,P,D的四边形是平行四边形,求所有符合条件的P点坐标.
5.如图所示,二次函数y=ax2+bx+c的图象过O(0,0),A(1,0),B(,)三点.
(1)求二次函数的解析式;
(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;
(3)在直线CD下方的二次函数的图象上有一动点P过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
参考答案
典例1 解:(1)证明:如图1所示,∵△ABC是等边三角形,
∴∠ABQ=∠CAP=60°,AB=CA,
又∵点P,Q运动速度相同,∴AP=BQ,
在△ABQ与△CAP中,∴△ABQ≌△CAP(SAS);
(2)点P,Q在AB,BC边上运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP.
∵∠QMC是△ACM的外角,∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC.
∵∠BAC=60°,∴∠QMC=60°;
(3)如图2所示,点PQ在运动到终点后继续在射线AB,BC上运动时,∠QMC不变.
理由:同理可得,△ABQ≌△CAP,∴∠BAQ=∠ACP.
∵∠QMC是△APM的外角,∴∠QMC=∠BAQ+∠APM.
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°.
即若点P,Q在运动到终点后继续在射线AB,BC上运动,∠QMC的度数为120°.
跟踪训练1
1.B
2.解:(1)证明:在等腰直角△ABC中,∠ACB=90°,AC=BC,F是AB中点,
∴∠A=∠FCE=∠ACF=45°,AF=CF.
在△ADF与△CEF中,AD=CE,∠A=∠FCE,AF=CF,∴△ADF≌△CEF(SAS);
(2)证明:由(1)可知△ADF≌△CEF,
∴DF=FE,∠AFD=∠EFC.∴△DFE是等腰三角形.
又∵∠AFD=∠CFE,∴∠AFD+∠DFC=∠CFE+∠DFC.∴∠AFC=∠DFE.
∵∠AFC=90°,∴∠DFE=90°.∴△DFE是等腰直角三角形;
(3)由(1)可知△ADF≌△CEF,∴AD=CE=5.
∵AC=BC,∴AC-AD=BC-CE,即CD=BE.
∴AC=AD+CD=AD+BE=5+7=12.
3.解:(1)∵A(4,4),B(6,0),
∴OA=,AB=.
故答案为:4,2;
(2)设直线AB的解析式为y=kx+b,
将A(4,4),B(6,0)代入得到,解得
∴直线AB的解析式为y=-2x+12,
由题意,点N的纵坐标为1,
令y=1,则1=-2x+12,∴x=.∴N(,1);
(3)当0<t<4时,令y=t,代入y=-2x+12,得到x=,∴N(,t).
∵∠AOB=∠AOP=45°,∠OPM=90°,∴OP=PM=t.
∴MN=PN-PM=-t=.故答案为:;
(4)如图所示,当t=时,MN==4,
设EM=m,则EN=4-m.
由题意S1·S2=·m×4×(4-m)×4=-4m2+16m=-4(m-2)2+16,
∵-4<0,∴m=2时,S1·S2有最大值,最大值为16.
故答案为:16.
典例2
解:(1)AE=AF.
∵AD=AB,四边形ABCD矩形,∴四边形ABCD是正方形.∴∠BAD=90°.
∵AF⊥AE,∴∠EAF=90°.∴∠EAB=∠FAD.
∴△EAB≌△FAD(AAS),∴AF=AE;
故答案为:AF=AE;
(2)AF=kAE.
证明:∵四边形ABCD是矩形,∴∠BAD=∠ABC=∠ADF=90°.∴∠FAD+∠FAB=90°.
∵AF⊥AE,∴∠EAF=90°.∴∠EAB+∠FAB=90°.∴∠EAB=∠FAD.
∵∠ABE=∠ADF,∴△ABE∽△ADF.
∴ .∵AD=kAB,∴.∴.∴AF=kAE.
(3)①如图1所示,当点F在DC上时,
∵四边形ABCD是矩形,∴AB=CD,AB∥CD.
∵AD=2AB=4,∴AB=2.∴CD=2.
∵CF=1,∴DF=CD-CF=2-1=1.
在Rt△ADF中,∠ADF=90°,∴AF=.
∵DF∥AB,∴∠GDF=∠GBA,∠GFD=∠GAB.∴△GDF∽△GBA.
∴.∵AF=GF+AG,∴AG=AF=.
∵△ABE∽△ADF,∴.∴AE=AF=×=.
在Rt△EAG中,∠EAG=90°,∴EG=.
②如图2所示,当点F在DC的延长线上时,DF=CD+CF=2+1=3,
在Rt△ADF中,∠ADF=90°.∴AF==5.
∵DF∥AB,∵∠GAB=∠GFD,∠GBA=∠GDF,∴△AGB∽△FGD.∴.
∵GF+AG=AF=5,∴AG=2.
∵△ABE∽△ADF,∴.∴AE=AF=×5=.
在Rt△EAG中,∠EAG=90°,∴.
综上所述,EG的长为或.
跟踪训练2
1.B 2.10
3.解:(1)证明:∵四边形ABCD是正方形,∴∠B=∠DAE=90°,AB=AD=BC.
∵点E,F分别是AB,BC的中点,∴AE=AB,BF=BC.∴AE=BF.
∴△ABF≌△DAE(SAS);
(2)在正方形ABCD中,AB∥CD,∠ADC=90°,AD=CD=2,
∴AC=.
∵AB∥CD,∴△AGE∽△CGD.∴,即,∴AG=;
(3)当BF=时,AG=AE,理由如下:
如图所示,设AF交CD于点M,
若使AG=AE=1,则有∠1=∠2.
∵AB∥CD,∴∠1=∠4.
又∵∠2=∠3,∴∠3=∠4.∴DM=MG.
在Rt△ADM中,AM2-DM2=AD2,即(DM+1)2-DM2=22,解得DM=,
∴CM=CD-DM=2-=.
∵AB∥CD,∴△ABF∽△MCF.∴,即.∴BF=.
故当BF=时,AG=AE.
4.解:(1)∵AB长是x2-3x-18=0的根,∴AB=6.
∵四边形ABCD是矩形,∴AD=BC,AB=CD=6,∠BCD=90°.
∵∠DBC=30°,∴BD=2CD=12,BC=CD=6.
∵∠DBC=30°,CN⊥BD,∴CN=BC=3.
故答案为:3.
(2)如图所示,过点M作MH⊥BD于H,
∵AD∥BC,∴∠ADB=∠DBC=30°.∴MH=MD=.
∵∠DBC=30°,CN⊥BD,∴BN=CN=9.
当0<1<时,△PMN的面积s=×(9-2t)×=-t2+t;
当t=时,点P与点N重合,s=0,
当<t≤6时,△PMN的面积s=×(2t-9)×=t2-t;
∴S=.
(3)如图所示,过点P作PE⊥BC于E,
当PN=PM=9-2t时,
∵PM2=MH2+PH2,∴(9-2t)2=(t)2+(12-2t-t)2.
∴t=3或t=.∴BP=6或.
当BP=6时,
∵∠DBC=30°,PE⊥BC,∴PE=BP=3,BE=PE=3.∴点P(3,3).
当BP=,同理可求点P(,),
当PN=NM=9-2t时,
∵NM2=MH2+NH2,∴(9-2t)2=(t)2+(t-3)2.
∴t=3或24(不合题意舍去)∴BP=6.∴点P(3,3).
综上所述:点P坐标为(3,3)或(,).
5.解:(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°.
在Rt△ABC中,AB=6,BC=8,根据勾股定理得,AC=10,
由运动知,CP=t=5,∴AP=AC-CP=5.∴AP=CP.
∵AD∥BC,∴∠PAF=∠PCE,∠AFP=∠CEP.
∴△APF≌△CPE(AAS).∴AF=CE;
(2)结论:AQ2+CE2=QE2,
理由:如图2所示,连接FQ,
由(1)知,△APF≌△CPE,∴AF=CE,PE=PF.∵EF⊥PQ,∴QE=QF.
在Rt△QAF中,根据勾股定理得,AQ2+AF2=QF2,∴AQ2+CE2=QE2;
(3)如图3所示,
由运动知,AQ=t,CP=t,∴AP=AC-CP=10-t.
∵FQ平分∠AFE,∴∠AFQ=∠PFQ.
∵∠FAQ=∠FPQ=90°,FQ=FQ,∴△FAQ≌△FPQ(AAS).
∴AQ=PQ=t,AF=PF.∴BQ=AB-AQ=6-t,∠FAC=∠FPA.
∵∠DAC=∠ACB,∠APF=∠CPE,∴∠ACB=∠CPE.
∴PE=CE,过点E作EN⊥AC于N.∴CN=CP=t,∠CNE=90°=∠ABC.
∵∠NCE=∠BCA,∴△CNE∽△CBA.∴.∴.∴CE=t.
∴PE=t,BE=BC-CE=8-t.
在Rt△QPE中,QE2=PQ2+PE2,在Rt△BQE中,QE2=BQ2+BE2,∴PQ2+PE2=BQ2+BE2.
∴t2+(t)2=(6-t)2+(8-t)2.∴t=.
∴CP=t=.∴AP=10-CP=.
∵AD∥BC,∴△APF∽△CPE.∴
典例3 解:(1)证明:连接OD,DB,
∵点E是线段OB的中点,DE⊥AB交⊙O于点D,∴DE垂直平分OB.∴DB=DO.
∵在⊙O中,DO=OB,∴DB=DO=OB.∴△ODB是等边三角形.∴∠BDO=∠DBO=60°.
∵BC=OB=BD,且∠DBE为△BDC的外角,∴∠BCD=∠BDC=∠DBO.
∵∠DBO=60°,∴∠CDB=30°.
∴∠ODC=∠BDO+∠BDC=60°+30°=90°.∴CD是⊙O的切线;
(2)这个确定的值是.
证明:连接OP,如图所示:
由已知可得:OP=OB=BC=2OE.∴.
又∵∠COP=∠POE,∴△OEP∽△OPC.∴ .
跟踪训练3
1.2或2 2.2 3.2 4.1或(11+6)
5.解:(1)∵AB是⊙O的直径,∴∠ACB=90°.
∵∠ABC=60°∴∠BAC=180°∠ACB-∠ABC=30°;
∴AB=2BC=4cm,即口O的直径为4cm.
(2)如图1所示,CD切⊙O于点C,连接 OC,
则OC=OB=×AB=2cm.∴CD⊥CO.∴∠OCD=90°.
∴∠BAC=30°.∴∠COD=2∠BAC=60°.
∴∠D=180°-∠COD-∠OCD=30°.∴OD=2OC=4cm.
∴BD=OD-OB=4-2=2(cm).∴当BD长为2cm,CD与O相切;
(3)根据题意,得BE=(4-2t)cm, BF=t cm,
如图2所示,当EF⊥BC时,△BEF为直角三角形,此时△BEF∽△BAC,
∴BE:BA=BF:BC.即(4-2t):4=t:2.解得t=1.
如图3所示,当EF⊥BA时,△BEF为直角三角形,此时△BEF∽△BCA,
∴BE:BC=BF:BA;即(4-2t):2=t:4;解得t=1.6.
∴当t=1s或t=1.6s时,△BEF为直角三角形.
典例4 解:(1)∵抛物线y=-x2+2x+c与y轴正半轴分别交于点B,∴点B(0,c).
∵OA=OB=c,∴点A(c,0).∴0=-c2+2c+c.∴c=3或0(舍去).
∴抛物线解析式为y=-x2+2x+3.
∵y=-x2+2x+3=-(x-1)2+4,∴顶点G为(1,4);
(2)∵y=-x2+2x+3=-(x-1)2+4,∴对称轴为直线x=1.
∵点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长
度和5个单位长度,
∴点M的横坐标为-2或4,点N的横坐标为6.
∴点M坐标为(-2,-5)或(4,-5),点N坐标(6,-21).
∵点Q为抛物线上点M,N之间(含点M,N)的一个动点,
∴当M(-2,-5),N(6,-21)时,-21≤yQ≤4;
当M(4,-5),N(6,-21)时,-21≤yQ≤-5.
跟踪训练4
1.D 2.1
3.解:(1)∵反比例函数y=(x>0)的图象经过点A(4,),∴m=4×=6.
∵AB交x轴于点C,C为线段AB的中点.∴C(2,0);
故答案为:6,(2,0);
(2)设直线AB的解析式为y=kx+b,
把A(4,),C(2,0)代入,得解得.
∴直线AB的解析式为y=.
∵点D为线段AB上的一个动点,∴设D(x,)(0<x≤4).
∵DE∥y轴,∴E(x,).∴S△ODE=.
∴当x=1时,△ODE的面积的最大值为.
4.解:(1)把点A(-3,)代入y=ax2,得=9a,∴a=.
∴抛物线的解析式为y=x2.
(2)设直线的解析式为y=kx+b,则有解得,
∴直线的解析式为y=-x+.
令x=0,得y=.∴C(0,).
由解得或∴B(1,).
如图1所示,过点A作AA1⊥x轴于点A1,过点B作BB1⊥x轴于点B1,则BB1∥OC∥AA1,
∴,.
∴,即MC2=MA·MB;
(3)如图2所示,设P(t,),
∵OC为一边且顶点为O,CP,D的四边形是平行四边形,
∴PD∥OC,PD=OC.∴D(t,-t+).∴.
整理,得t2+2t-6=0或t2+2t=0,解得t=-1-或-1+或-2或0(舍去).
∴P(-1-,2+)或(1+,2-)或(-2,1).
5.解:(1)将点O,A,B的坐标代入抛物线表达式,
得,解得,故抛物线的表达式为:;
(2)由点B的坐标知,直线BO的倾斜角为30°,则OB中垂线(CD)与x负半轴的夹角为60°,故设CD的表达式为:y=-x+b,而OB中点的坐标为(),
将该点坐标代入CD表达式并解得b=,故直线CD的表达式为:y=-x+;
(3)过点P作y轴的平行线交CD于点Q,
设点P(x,),则点Q(x,-x+),
则PQ=,
∵故PQ有最大值,此时点P的坐标为.
_21?????????è?????(www.21cnjy.com)_
几何动态探究专题
专题解读
几何动态问题是近些年来中考数学的热点题型.纵观全国各地的中考数学试卷,动态几何型综合题常常出现在一张试卷的压轴题位置,估计这一趋势在今后几年的中考中仍将持续.这类试题信息量大,综合性较强,往往涉及到函数、直线型、圆等初中数学的多个重点考查对象,对获取信息和处理信息的能力要求较高,应加大训练的力度.
解题策略:几何动态型问题就是在线段、三角形、矩形圆等一些几何图形上,设计一个或几个动点(或线或面),并对这些点(或线或面)在运动变化的过程中相伴随着的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等进行研究考查.动态型问题常常集几何、代数知识于一体,数形结合,有较强的综合性.解决动态型问题需要用运动与变化的眼光去观察和研究图形,把握动点(或线或面)运动与变化的全过程,抓住其中的等量关系和变量关系,并特别关注一些不变量、不变关系或特殊关系,“动中求静,静中求解”.
几何动态型问题有时把函数、方程、不等式联系起来,当求有关图形的变量之间关系时,常建立函数模型或不等式模型求解;当求图形之间的特殊位置关系和一些特殊的值时,通常建立方程模型去求解.
考点一 探究三角形中的动点问题
典例1 如图所示,点P,Q分别是等边△ABC边AB,BC上的动点(端点除外),点P,Q以相同的速度,同时从点A,B出发.
(1)如图1所示,连接AQ,CP.求证:△ABQ≌△CAP;
(2)如图1所示,当点P,Q分别在AB,BC边上运动时,AQ,CP相交于点M,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数;
(3)如图2所示,当点P,Q在AB,BC的延长线上运动时,直线AQ,CP相交于M,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
思路导引
(1)根据等边三角形的性质,利用SAS证明△ABQ≌△CAP即可;
(2)先判定△ABQ≌△CAP,根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=60°;(3)先判定△ABQ≌△CAP,根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=120°.
名师点拨
此题是三角形的动态综合题,主要考查了等边三角形的性质、全等三角形的判定与性质等知识的综合应用.解决问题的关键是掌握全等三角形的判定方法:两边及其夹角分别对应相等的两个三角形全等.解题时注意运用全等三角形的对应边相等、对应角相等的性质,体会在运动变化过程中蕴含着不变的量.
跟踪训练1
1.如图所示,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点PAP→B的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
2.如图所示,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D,E分别在ACBC边上运动,且始终保持AD=CE.连接DE,DF,EF(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形;
(3)若AD=5,BE=7,求AC的长.
3.如图所示,在平面直角坐标系中,△AOB的顶点O是坐标原点,点A的坐标为(4,4),点B的坐标为(6,0),动点P从O开始以每秒1个单位长度的速度沿y轴正方向运动,设运动的时间为t秒(0<t<4),过点P作PN∥x轴,分别交AO,AB于点 M,N.
(1)填空:AO的长为__________,AB的长为__________.
(2)当t=1时,求点N的坐标;
(3)请直接写出MN的长为_________(用含t的代数式表示);
(4)点E是线段MN上一动点(点E不与点M,N重合),△AOE和△ABE的面积分别表示为S1和S2,当t=时,请直接写出S1·S2(即S1与S2的积)的最大值为__________.
考点二 探究特殊四边形中的动点问题
典例2 如图所示,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1所示,若k=1,则AF与AE之间的数量关系是__________;
(2)如图2所示,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)
(3)若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.
思路导引
(1)证明△EAB≌△FAD(AAS),由全等三角形的性质得出AF=AE;
(2)证明△ABE∽△ADF,由相似三角形的性质得出,则可得出结论;
(3)①当点F在DC上时,证得△GDF∽△GBA,得出,求出AG=AF=.由△ABE∽△ADF可得出,求出AE=则可得出答案;②当点F在DC的延长线上时,同理可求出EG的长.
名师点拨
本题是相似形综合题,考查了全等三角形的判定与性质,正方形的性质,矩形的性质,相似三角形的判定与性质,勾股定理等知识,熟练掌握相似三角形的判定与性质是解题的关键.注意在动态变化过程中,蕴含着确定的数量关系.
跟踪训练2
1.如图所示,正方形ABCD的边长为4点E在AB上且BE=1,F为对角线AC上一动点,则△BFE周长的最小值为( )
A.5 B.6 C.7 D.8
2.如图所示,在矩形ABCD中,AD=12,AB=8,E是AB上一点,且EB=3,F是BC上一动点,若将△EBF沿EF对折后,点B落在点P处,则点P到点D的最短距离为_________.
3.四边形ABCD是边长为2的正方形,E是AB的中点,连接DE,点F是射线BC上一动点(不与点B重合),连接AF,交DE于点G.
(1)如图1所示,当点F是BC边的中点时,求证:△ABF≌△DAE;
(2)如图2所示,当点F与点C重合时,求AG的长;(3)在点F运动的过程中,当线段BF为何值时,AG=AE?请说明理由.
4.如图所示,在平面直角坐标系中,矩形ABCD的边AB的长是x2-3x-18=0的根,连接BD,∠DBC=30°,并过点C作CN⊥BD,垂足为N,动点P从B点以每秒2个单位长度的速度沿BD方向匀速运动到D点为止;点M沿线段DA以每秒3个单位长度的速度由点D向点A匀速运动,到点A为止,点P与点M同时出发,设运动时间为t秒(t>0).
(1)线段CN=___________;
(2)连接PM和MN,求△PMN的面积s与运动时间t的函数关系式;
(3)在整个运动过程中,当△PMN是以PN为腰的等腰三角形时,直接写出点P的坐标.
5.如图1所示,在矩形ABCD中,AB=6,BC=8,动点P,Q分别从C点,A点同时以每秒1个单位长度的速度出发,且分别在边CA,AB上沿C→A,A→B的方向运动,当点Q运动到点B时,P,Q两点同时停止运动,设点P运动的时间为t(s),连接PQ,过点P作PE⊥PQ,PE与边BC相交于点E,连接QE.
(1)如图2所示,当t=5s时,延长EP交边AD于点F.求证:AF=CE;
(2)在(1)的条件下,试探究线段AQ,QE,CE三者之间的等量关系,并加以证明;
(3)如图3所示,当t>s时,延长EP交边AD于点F,连接FQ,若FQ平分∠AFP,求的值.
考点三 探究圆中的动点问题
典例3 古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆.”请研究如下美丽的圆.如图所示,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接 CD, PE, PC.
(1)求证:CD是⊙O的切线;
(2)小明在研究的过程中发现是一个确定的值回答这个确定的值是多少?并对小明发现的结论加以证明.
思路导引
(1)连接OD,DB,由已知可知DE垂直平分OB,则DB=DO,再由圆的半径相等,可得DB=DO=OB,即△ODB是等边三角形,则∠BDO=60°,再由等腰三角形的性质及三角形的外角性质可得∠CDB=30°,从而可得∠ODC=90°,按照切线的判定定理可得结论;
(2)连接OP,先由已知条件得OP=OB=BC=2OE,再利用两组边成比例,夹角相等来证明△OEP∽△OPC,按照相似三角形的性质得出比例式,则可得答案.
名师点拨
本题考查了切线的判定与性质及相似三角形的判定与性质,熟练掌握相关性质及定理是解题的关键.注意在动点的运动过程中存在确定的线段比值(即确定的数量关系).
跟踪训练3
1.如图所示,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连接OC,AC,当△OAC是直角三角形时,其斜边长为_________.
2.如图所示,已知直线y=-x+4与x,y轴交于AB两点,⊙O的半径为1,P为AB上一动点,PQ切⊙O于Q点.当线段PQ长取最小值时,直线PQ交y轴于M点,a为过点M的一条直线,则点P到直线a的距离的最大值为__________.
3.如图所示,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y=x-3与x轴、y轴分别交于点D,E,则△CDE面积的最小值为____________.
4.如图所示,半径为2cm的⊙O与边长为2cm的正方形ABCD的边AB相切于E,点F为正方形的中心,直线OE过F点.当正方形ABCD沿直线OF以每秒(2-)cm的速度向左运动________秒时,⊙O与正方形重叠部分的面积为()cm2.
5.如图所示,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连接CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2 cm/s的速度从A点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动,设运动时间为t(s)(0<1<2),连接EF,当t为何值时,△BEF为直角三角形.
考点四 探究函数中的动点问题
典例4 如图所示,抛物线y=-x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,
且OA=OB,点G为抛物线的顶点.
(1)求抛物线的解析式及点G的坐标;
(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的纵坐标y的取值范围.
思路导引
(1)先求出点B,点A坐标,代入解析式可求c的值,即可求解;
(2)先求出点M,点N坐标,即可求解.
名师点拨
本题考查了待定系数法求二次函数解析式,二次函数的性质,二次函数图象上点的坐标特征,熟练运用二次函数的性质是解决问题的关键.注意体会动态变化过程与函数思想的密切联系.
跟踪训练4
1.如图所示,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
2.如图所示,等腰△ABC的两个顶点A(-1,-4),B(-4,-1)在反比例函数y=(x<0)的图象上,AC=BC.过点C作边AB的垂线交反比例函数y=(x<0)的图象于点D,动点P从点D出发,沿射线CD方向运动3个单位长度,到达反比例函数y=(x>0)图象上一点,则k2=___________.
3.如图所示,在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(4,),点B在y轴的负半轴上,AB交x轴于点C,C为线段AB的中点.
(1)m=________,点C的坐标为___________;
(2)若点D为线段AB上的一个动点,过点D作DE∥y轴,交反比例函数图象于点E,求△ODE面积的最大值.
4.如图所示,已知抛物线y=ax2过点A(-3,).
(1)求抛物线的解析式;
(2)已知直线过点A,M(,0)且与抛物线交于另一点B,与y轴交于点C,求证:MC2=MA·MB;
(3)若点P,D分别是抛物线与直线l上的动点,以OC为一边且顶点为O,C,P,D的四边形是平行四边形,求所有符合条件的P点坐标.
5.如图所示,二次函数y=ax2+bx+c的图象过O(0,0),A(1,0),B(,)三点.
(1)求二次函数的解析式;
(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;
(3)在直线CD下方的二次函数的图象上有一动点P过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
参考答案
典例1 解:(1)证明:如图1所示,∵△ABC是等边三角形,
∴∠ABQ=∠CAP=60°,AB=CA,
又∵点P,Q运动速度相同,∴AP=BQ,
在△ABQ与△CAP中,∴△ABQ≌△CAP(SAS);
(2)点P,Q在AB,BC边上运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP.
∵∠QMC是△ACM的外角,∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC.
∵∠BAC=60°,∴∠QMC=60°;
(3)如图2所示,点PQ在运动到终点后继续在射线AB,BC上运动时,∠QMC不变.
理由:同理可得,△ABQ≌△CAP,∴∠BAQ=∠ACP.
∵∠QMC是△APM的外角,∴∠QMC=∠BAQ+∠APM.
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°.
即若点P,Q在运动到终点后继续在射线AB,BC上运动,∠QMC的度数为120°.
跟踪训练1
1.B
2.解:(1)证明:在等腰直角△ABC中,∠ACB=90°,AC=BC,F是AB中点,
∴∠A=∠FCE=∠ACF=45°,AF=CF.
在△ADF与△CEF中,AD=CE,∠A=∠FCE,AF=CF,∴△ADF≌△CEF(SAS);
(2)证明:由(1)可知△ADF≌△CEF,
∴DF=FE,∠AFD=∠EFC.∴△DFE是等腰三角形.
又∵∠AFD=∠CFE,∴∠AFD+∠DFC=∠CFE+∠DFC.∴∠AFC=∠DFE.
∵∠AFC=90°,∴∠DFE=90°.∴△DFE是等腰直角三角形;
(3)由(1)可知△ADF≌△CEF,∴AD=CE=5.
∵AC=BC,∴AC-AD=BC-CE,即CD=BE.
∴AC=AD+CD=AD+BE=5+7=12.
3.解:(1)∵A(4,4),B(6,0),
∴OA=,AB=.
故答案为:4,2;
(2)设直线AB的解析式为y=kx+b,
将A(4,4),B(6,0)代入得到,解得
∴直线AB的解析式为y=-2x+12,
由题意,点N的纵坐标为1,
令y=1,则1=-2x+12,∴x=.∴N(,1);
(3)当0<t<4时,令y=t,代入y=-2x+12,得到x=,∴N(,t).
∵∠AOB=∠AOP=45°,∠OPM=90°,∴OP=PM=t.
∴MN=PN-PM=-t=.故答案为:;
(4)如图所示,当t=时,MN==4,
设EM=m,则EN=4-m.
由题意S1·S2=·m×4×(4-m)×4=-4m2+16m=-4(m-2)2+16,
∵-4<0,∴m=2时,S1·S2有最大值,最大值为16.
故答案为:16.
典例2
解:(1)AE=AF.
∵AD=AB,四边形ABCD矩形,∴四边形ABCD是正方形.∴∠BAD=90°.
∵AF⊥AE,∴∠EAF=90°.∴∠EAB=∠FAD.
∴△EAB≌△FAD(AAS),∴AF=AE;
故答案为:AF=AE;
(2)AF=kAE.
证明:∵四边形ABCD是矩形,∴∠BAD=∠ABC=∠ADF=90°.∴∠FAD+∠FAB=90°.
∵AF⊥AE,∴∠EAF=90°.∴∠EAB+∠FAB=90°.∴∠EAB=∠FAD.
∵∠ABE=∠ADF,∴△ABE∽△ADF.
∴ .∵AD=kAB,∴.∴.∴AF=kAE.
(3)①如图1所示,当点F在DC上时,
∵四边形ABCD是矩形,∴AB=CD,AB∥CD.
∵AD=2AB=4,∴AB=2.∴CD=2.
∵CF=1,∴DF=CD-CF=2-1=1.
在Rt△ADF中,∠ADF=90°,∴AF=.
∵DF∥AB,∴∠GDF=∠GBA,∠GFD=∠GAB.∴△GDF∽△GBA.
∴.∵AF=GF+AG,∴AG=AF=.
∵△ABE∽△ADF,∴.∴AE=AF=×=.
在Rt△EAG中,∠EAG=90°,∴EG=.
②如图2所示,当点F在DC的延长线上时,DF=CD+CF=2+1=3,
在Rt△ADF中,∠ADF=90°.∴AF==5.
∵DF∥AB,∵∠GAB=∠GFD,∠GBA=∠GDF,∴△AGB∽△FGD.∴.
∵GF+AG=AF=5,∴AG=2.
∵△ABE∽△ADF,∴.∴AE=AF=×5=.
在Rt△EAG中,∠EAG=90°,∴.
综上所述,EG的长为或.
跟踪训练2
1.B 2.10
3.解:(1)证明:∵四边形ABCD是正方形,∴∠B=∠DAE=90°,AB=AD=BC.
∵点E,F分别是AB,BC的中点,∴AE=AB,BF=BC.∴AE=BF.
∴△ABF≌△DAE(SAS);
(2)在正方形ABCD中,AB∥CD,∠ADC=90°,AD=CD=2,
∴AC=.
∵AB∥CD,∴△AGE∽△CGD.∴,即,∴AG=;
(3)当BF=时,AG=AE,理由如下:
如图所示,设AF交CD于点M,
若使AG=AE=1,则有∠1=∠2.
∵AB∥CD,∴∠1=∠4.
又∵∠2=∠3,∴∠3=∠4.∴DM=MG.
在Rt△ADM中,AM2-DM2=AD2,即(DM+1)2-DM2=22,解得DM=,
∴CM=CD-DM=2-=.
∵AB∥CD,∴△ABF∽△MCF.∴,即.∴BF=.
故当BF=时,AG=AE.
4.解:(1)∵AB长是x2-3x-18=0的根,∴AB=6.
∵四边形ABCD是矩形,∴AD=BC,AB=CD=6,∠BCD=90°.
∵∠DBC=30°,∴BD=2CD=12,BC=CD=6.
∵∠DBC=30°,CN⊥BD,∴CN=BC=3.
故答案为:3.
(2)如图所示,过点M作MH⊥BD于H,
∵AD∥BC,∴∠ADB=∠DBC=30°.∴MH=MD=.
∵∠DBC=30°,CN⊥BD,∴BN=CN=9.
当0<1<时,△PMN的面积s=×(9-2t)×=-t2+t;
当t=时,点P与点N重合,s=0,
当<t≤6时,△PMN的面积s=×(2t-9)×=t2-t;
∴S=.
(3)如图所示,过点P作PE⊥BC于E,
当PN=PM=9-2t时,
∵PM2=MH2+PH2,∴(9-2t)2=(t)2+(12-2t-t)2.
∴t=3或t=.∴BP=6或.
当BP=6时,
∵∠DBC=30°,PE⊥BC,∴PE=BP=3,BE=PE=3.∴点P(3,3).
当BP=,同理可求点P(,),
当PN=NM=9-2t时,
∵NM2=MH2+NH2,∴(9-2t)2=(t)2+(t-3)2.
∴t=3或24(不合题意舍去)∴BP=6.∴点P(3,3).
综上所述:点P坐标为(3,3)或(,).
5.解:(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°.
在Rt△ABC中,AB=6,BC=8,根据勾股定理得,AC=10,
由运动知,CP=t=5,∴AP=AC-CP=5.∴AP=CP.
∵AD∥BC,∴∠PAF=∠PCE,∠AFP=∠CEP.
∴△APF≌△CPE(AAS).∴AF=CE;
(2)结论:AQ2+CE2=QE2,
理由:如图2所示,连接FQ,
由(1)知,△APF≌△CPE,∴AF=CE,PE=PF.∵EF⊥PQ,∴QE=QF.
在Rt△QAF中,根据勾股定理得,AQ2+AF2=QF2,∴AQ2+CE2=QE2;
(3)如图3所示,
由运动知,AQ=t,CP=t,∴AP=AC-CP=10-t.
∵FQ平分∠AFE,∴∠AFQ=∠PFQ.
∵∠FAQ=∠FPQ=90°,FQ=FQ,∴△FAQ≌△FPQ(AAS).
∴AQ=PQ=t,AF=PF.∴BQ=AB-AQ=6-t,∠FAC=∠FPA.
∵∠DAC=∠ACB,∠APF=∠CPE,∴∠ACB=∠CPE.
∴PE=CE,过点E作EN⊥AC于N.∴CN=CP=t,∠CNE=90°=∠ABC.
∵∠NCE=∠BCA,∴△CNE∽△CBA.∴.∴.∴CE=t.
∴PE=t,BE=BC-CE=8-t.
在Rt△QPE中,QE2=PQ2+PE2,在Rt△BQE中,QE2=BQ2+BE2,∴PQ2+PE2=BQ2+BE2.
∴t2+(t)2=(6-t)2+(8-t)2.∴t=.
∴CP=t=.∴AP=10-CP=.
∵AD∥BC,∴△APF∽△CPE.∴
典例3 解:(1)证明:连接OD,DB,
∵点E是线段OB的中点,DE⊥AB交⊙O于点D,∴DE垂直平分OB.∴DB=DO.
∵在⊙O中,DO=OB,∴DB=DO=OB.∴△ODB是等边三角形.∴∠BDO=∠DBO=60°.
∵BC=OB=BD,且∠DBE为△BDC的外角,∴∠BCD=∠BDC=∠DBO.
∵∠DBO=60°,∴∠CDB=30°.
∴∠ODC=∠BDO+∠BDC=60°+30°=90°.∴CD是⊙O的切线;
(2)这个确定的值是.
证明:连接OP,如图所示:
由已知可得:OP=OB=BC=2OE.∴.
又∵∠COP=∠POE,∴△OEP∽△OPC.∴ .
跟踪训练3
1.2或2 2.2 3.2 4.1或(11+6)
5.解:(1)∵AB是⊙O的直径,∴∠ACB=90°.
∵∠ABC=60°∴∠BAC=180°∠ACB-∠ABC=30°;
∴AB=2BC=4cm,即口O的直径为4cm.
(2)如图1所示,CD切⊙O于点C,连接 OC,
则OC=OB=×AB=2cm.∴CD⊥CO.∴∠OCD=90°.
∴∠BAC=30°.∴∠COD=2∠BAC=60°.
∴∠D=180°-∠COD-∠OCD=30°.∴OD=2OC=4cm.
∴BD=OD-OB=4-2=2(cm).∴当BD长为2cm,CD与O相切;
(3)根据题意,得BE=(4-2t)cm, BF=t cm,
如图2所示,当EF⊥BC时,△BEF为直角三角形,此时△BEF∽△BAC,
∴BE:BA=BF:BC.即(4-2t):4=t:2.解得t=1.
如图3所示,当EF⊥BA时,△BEF为直角三角形,此时△BEF∽△BCA,
∴BE:BC=BF:BA;即(4-2t):2=t:4;解得t=1.6.
∴当t=1s或t=1.6s时,△BEF为直角三角形.
典例4 解:(1)∵抛物线y=-x2+2x+c与y轴正半轴分别交于点B,∴点B(0,c).
∵OA=OB=c,∴点A(c,0).∴0=-c2+2c+c.∴c=3或0(舍去).
∴抛物线解析式为y=-x2+2x+3.
∵y=-x2+2x+3=-(x-1)2+4,∴顶点G为(1,4);
(2)∵y=-x2+2x+3=-(x-1)2+4,∴对称轴为直线x=1.
∵点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长
度和5个单位长度,
∴点M的横坐标为-2或4,点N的横坐标为6.
∴点M坐标为(-2,-5)或(4,-5),点N坐标(6,-21).
∵点Q为抛物线上点M,N之间(含点M,N)的一个动点,
∴当M(-2,-5),N(6,-21)时,-21≤yQ≤4;
当M(4,-5),N(6,-21)时,-21≤yQ≤-5.
跟踪训练4
1.D 2.1
3.解:(1)∵反比例函数y=(x>0)的图象经过点A(4,),∴m=4×=6.
∵AB交x轴于点C,C为线段AB的中点.∴C(2,0);
故答案为:6,(2,0);
(2)设直线AB的解析式为y=kx+b,
把A(4,),C(2,0)代入,得解得.
∴直线AB的解析式为y=.
∵点D为线段AB上的一个动点,∴设D(x,)(0<x≤4).
∵DE∥y轴,∴E(x,).∴S△ODE=.
∴当x=1时,△ODE的面积的最大值为.
4.解:(1)把点A(-3,)代入y=ax2,得=9a,∴a=.
∴抛物线的解析式为y=x2.
(2)设直线的解析式为y=kx+b,则有解得,
∴直线的解析式为y=-x+.
令x=0,得y=.∴C(0,).
由解得或∴B(1,).
如图1所示,过点A作AA1⊥x轴于点A1,过点B作BB1⊥x轴于点B1,则BB1∥OC∥AA1,
∴,.
∴,即MC2=MA·MB;
(3)如图2所示,设P(t,),
∵OC为一边且顶点为O,CP,D的四边形是平行四边形,
∴PD∥OC,PD=OC.∴D(t,-t+).∴.
整理,得t2+2t-6=0或t2+2t=0,解得t=-1-或-1+或-2或0(舍去).
∴P(-1-,2+)或(1+,2-)或(-2,1).
5.解:(1)将点O,A,B的坐标代入抛物线表达式,
得,解得,故抛物线的表达式为:;
(2)由点B的坐标知,直线BO的倾斜角为30°,则OB中垂线(CD)与x负半轴的夹角为60°,故设CD的表达式为:y=-x+b,而OB中点的坐标为(),
将该点坐标代入CD表达式并解得b=,故直线CD的表达式为:y=-x+;
(3)过点P作y轴的平行线交CD于点Q,
设点P(x,),则点Q(x,-x+),
则PQ=,
∵故PQ有最大值,此时点P的坐标为.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
