圆的标准方程2
图片预览





文档简介
(共16张PPT)
圆的标准方程
A
r
x
y
O
赵州桥,建于隋炀帝大业年间(595-605年),至今已有1400年的历史,出自著名匠师李春之手,是今天世界上最古老的单肩石拱桥,是世界造桥史上的一个创造。
问题 : 假设桥梁圆拱损坏需修缮,若你修缮专家之一,那你该怎样去修缮桥梁圆拱呢
温故知新:
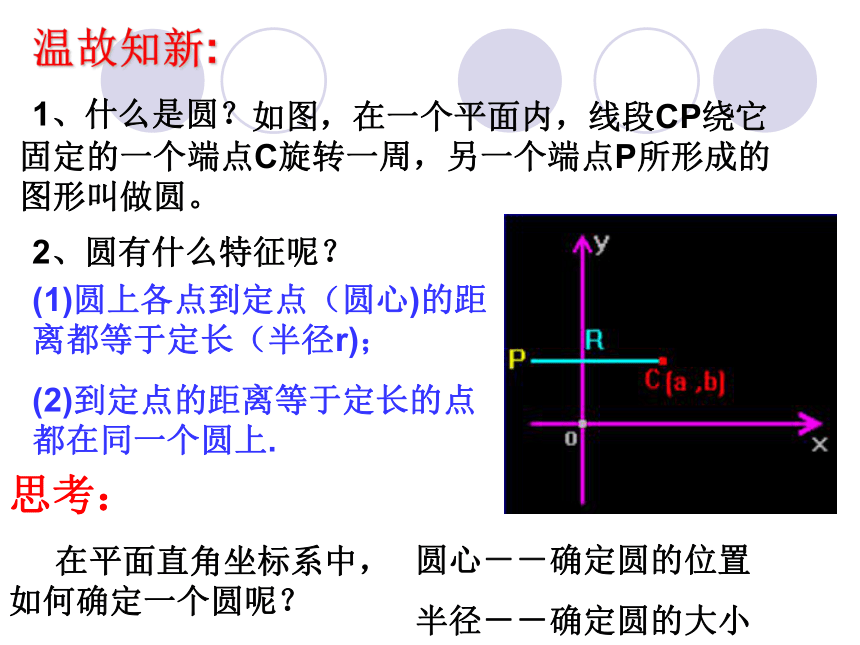
1、什么是圆?
如图,在一个平面内,线段CP绕它固定的一个端点C旋转一周,另一个端点P所形成的图形叫做圆。
2、圆有什么特征呢?
思考:
在平面直角坐标系中,如何确定一个圆呢?
圆心--确定圆的位置
半径--确定圆的大小
(1)圆上各点到定点(圆心)的距离都等于定长(半径r);
(2)到定点的距离等于定长的点都在同一个圆上.
A
M
r
x
O
y
设M(x,y)是圆上任意一点,
根据定义,点M到圆心A的 距离等于r,所以圆心为A的圆就是集合
P={M| |MA|=r}
由两点间的距离公式,点M适合的条件可表示为:
(x-a) 2 + (y-b) 2 = r
把上式两边平方得:
(x-a) 2 + (y-b) 2 = r2
(x-a) 2 + (y-b) 2 = r2
问题: 1、这条方程是圆的方程吗?为什么?
2、以这个方程的根为坐标的点都在圆上吗?为什么?
称为圆心为A(a,b),半径长为r的圆的标准方程
问题:圆的标准方程有什么特征
特别地:圆心在原点,半径为r的圆的方程是什么?
(1)有两个变量x,y,形式都是与某个实数差的平方;
(2)两个变量的系数都是1
(3)方程的右边是某个实数的平方,也就是一定为正数。
x 2 +y 2 = r2
3、已知圆 (x – 2 )2+(y + 3 )2=25 ,判断点 是否在圆上?
1、圆心为 ,半径长等于5的圆的方程为( )
A (x – 2 )2+(y – 3 )2=25 B (x – 2 )2+(y + 3 )2=25
C (x – 2 )2+(y + 3 )2=5 D (x + 2 )2+(y – 3 )2=5
2、圆 (x-2)2+ y2=2的圆心C的坐标为____,半径r =____
练习
点 呢?
点 呢?
重要结论:
点P(x0,y0)与圆(x-a)2+(y-b)2=r2
的位置关系:
问题 1: 假设桥梁圆拱损坏需修缮,若你修缮专家之一,那你该如何设计方案,去修缮桥梁圆拱呢
若现在已知圆拱上的三点A(5,1),B(7,-3),C(2,-8),
你能求出圆拱所在的圆的标准方程吗
问题2: 已知圆心为C的圆经过点A(1,1),B(2,-2),且圆心C在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
(1) 圆心为C(a,b),半径为r 的圆的标准方程为
(x-a) 2 + (y-b) 2 = r2
当圆心在原点时 ,圆的标准方程为: x2 + y2 = r2
(2)推导圆的标准方程的方法与步骤?
(3)点与圆的位置关系?
(4) 如何求圆的标准方程 必须具备三个独立的条件
(5)如何利用圆的标准方程解决实际问题
课堂小结:
问题3、某施工队要建一座圆拱桥,其跨度为20m, 拱高为4m。求该圆拱桥所在的圆的方程。
解:以圆拱所对的的弦所在的直线为x轴,弦的中点为原点建立如图所示的坐标系,设圆心坐标是(0,b)圆的半径是r ,则圆的方程是x2+(y-b)2=r2 。
把P(0,4) B(10,0)代入圆的方程得方程组:
02+(4-b)2= r2
102+(0-b)2=r2
解得:b= -10.5 r2=14.52
所以圆的方程是: x2+(y+10.5)2=14.52
A (-10,0)
B (10,0)
P (0,4)
y
x
O
变一:施工队认为跨度远了,准备在中间每隔4m建一根柱子。试给他们计算中间两根柱子的长度。
y
x
A
B
P
O
E
F
G
H
C
D
R
T
变二:已知一条满载货物的集装箱船,该船及货物离水面的高度是2米,船宽4米,问该船能否通过该桥?若能,那么船在什么区域内可通过?若不能,说明理由。
x2+(y+10.5)2=14.52
令x=2或-2即可
Y=3.86
圆的标准方程
A
r
x
y
O
赵州桥,建于隋炀帝大业年间(595-605年),至今已有1400年的历史,出自著名匠师李春之手,是今天世界上最古老的单肩石拱桥,是世界造桥史上的一个创造。
问题 : 假设桥梁圆拱损坏需修缮,若你修缮专家之一,那你该怎样去修缮桥梁圆拱呢
温故知新:
1、什么是圆?
如图,在一个平面内,线段CP绕它固定的一个端点C旋转一周,另一个端点P所形成的图形叫做圆。
2、圆有什么特征呢?
思考:
在平面直角坐标系中,如何确定一个圆呢?
圆心--确定圆的位置
半径--确定圆的大小
(1)圆上各点到定点(圆心)的距离都等于定长(半径r);
(2)到定点的距离等于定长的点都在同一个圆上.
A
M
r
x
O
y
设M(x,y)是圆上任意一点,
根据定义,点M到圆心A的 距离等于r,所以圆心为A的圆就是集合
P={M| |MA|=r}
由两点间的距离公式,点M适合的条件可表示为:
(x-a) 2 + (y-b) 2 = r
把上式两边平方得:
(x-a) 2 + (y-b) 2 = r2
(x-a) 2 + (y-b) 2 = r2
问题: 1、这条方程是圆的方程吗?为什么?
2、以这个方程的根为坐标的点都在圆上吗?为什么?
称为圆心为A(a,b),半径长为r的圆的标准方程
问题:圆的标准方程有什么特征
特别地:圆心在原点,半径为r的圆的方程是什么?
(1)有两个变量x,y,形式都是与某个实数差的平方;
(2)两个变量的系数都是1
(3)方程的右边是某个实数的平方,也就是一定为正数。
x 2 +y 2 = r2
3、已知圆 (x – 2 )2+(y + 3 )2=25 ,判断点 是否在圆上?
1、圆心为 ,半径长等于5的圆的方程为( )
A (x – 2 )2+(y – 3 )2=25 B (x – 2 )2+(y + 3 )2=25
C (x – 2 )2+(y + 3 )2=5 D (x + 2 )2+(y – 3 )2=5
2、圆 (x-2)2+ y2=2的圆心C的坐标为____,半径r =____
练习
点 呢?
点 呢?
重要结论:
点P(x0,y0)与圆(x-a)2+(y-b)2=r2
的位置关系:
问题 1: 假设桥梁圆拱损坏需修缮,若你修缮专家之一,那你该如何设计方案,去修缮桥梁圆拱呢
若现在已知圆拱上的三点A(5,1),B(7,-3),C(2,-8),
你能求出圆拱所在的圆的标准方程吗
问题2: 已知圆心为C的圆经过点A(1,1),B(2,-2),且圆心C在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
(1) 圆心为C(a,b),半径为r 的圆的标准方程为
(x-a) 2 + (y-b) 2 = r2
当圆心在原点时 ,圆的标准方程为: x2 + y2 = r2
(2)推导圆的标准方程的方法与步骤?
(3)点与圆的位置关系?
(4) 如何求圆的标准方程 必须具备三个独立的条件
(5)如何利用圆的标准方程解决实际问题
课堂小结:
问题3、某施工队要建一座圆拱桥,其跨度为20m, 拱高为4m。求该圆拱桥所在的圆的方程。
解:以圆拱所对的的弦所在的直线为x轴,弦的中点为原点建立如图所示的坐标系,设圆心坐标是(0,b)圆的半径是r ,则圆的方程是x2+(y-b)2=r2 。
把P(0,4) B(10,0)代入圆的方程得方程组:
02+(4-b)2= r2
102+(0-b)2=r2
解得:b= -10.5 r2=14.52
所以圆的方程是: x2+(y+10.5)2=14.52
A (-10,0)
B (10,0)
P (0,4)
y
x
O
变一:施工队认为跨度远了,准备在中间每隔4m建一根柱子。试给他们计算中间两根柱子的长度。
y
x
A
B
P
O
E
F
G
H
C
D
R
T
变二:已知一条满载货物的集装箱船,该船及货物离水面的高度是2米,船宽4米,问该船能否通过该桥?若能,那么船在什么区域内可通过?若不能,说明理由。
x2+(y+10.5)2=14.52
令x=2或-2即可
Y=3.86
