七年级数学第七章三角形的内角和
文档属性
| 名称 | 七年级数学第七章三角形的内角和 |  | |
| 格式 | zip | ||
| 文件大小 | 60.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-13 11:09:39 | ||
图片预览


文档简介
(共19张PPT)
三角形的内角
人教版数学七年级(下) 第七章 第三节
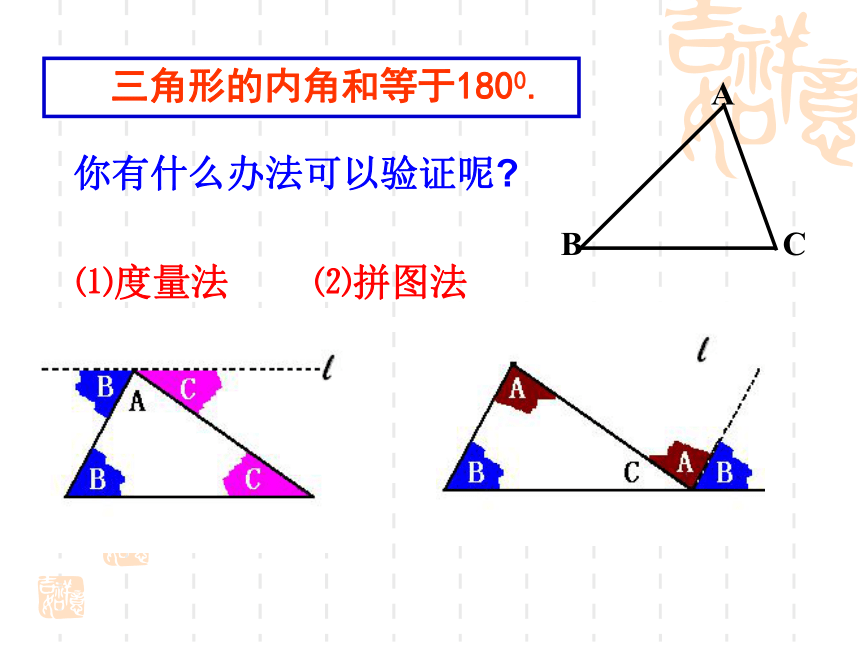
你有什么办法可以验证呢
三角形的内角和等于1800.
⑴度量法 ⑵拼图法
A
B
C
A
B
C
E
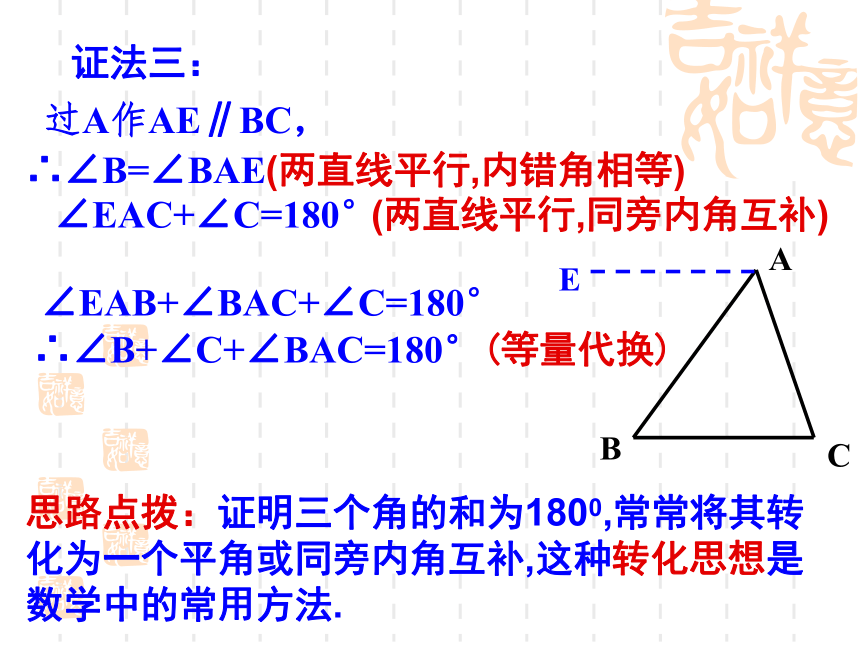
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°(等量代换)
∠EAC+∠C=180°
思路点拨:证明三个角的和为1800,常常将其转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
证法三:
闯关练习---分组抢答竞赛:
1、在老师示意开始抢答时,各小组举手抢答, 举手最多的小组获得答题权。
2、答对者小组获得相应的分数。答错者将答题权转给对方。
3、积分最高者为优胜组。
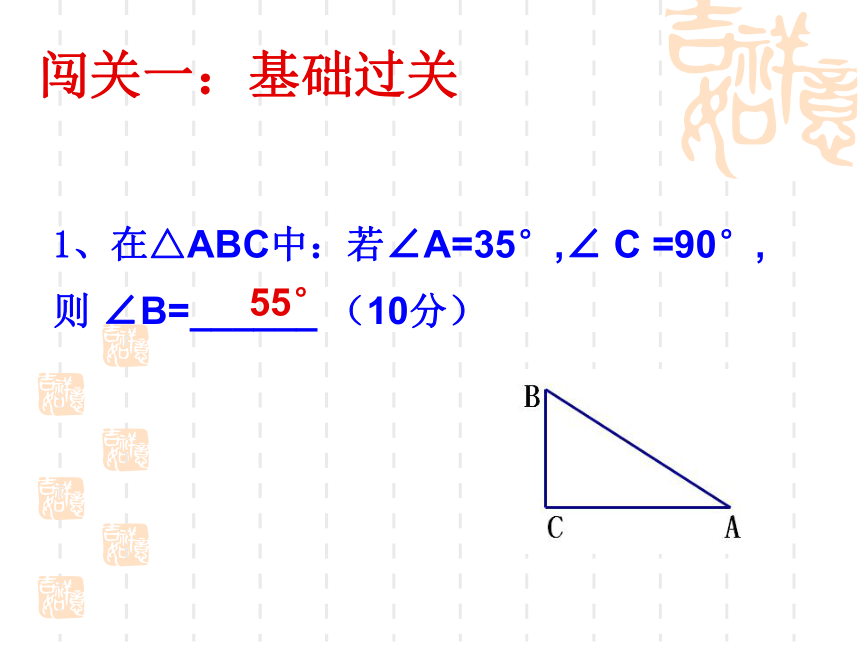
闯关一:基础过关
1、在△ABC中:若∠A=35°,∠ C =90°,
则 ∠B=______ (10分)
55°
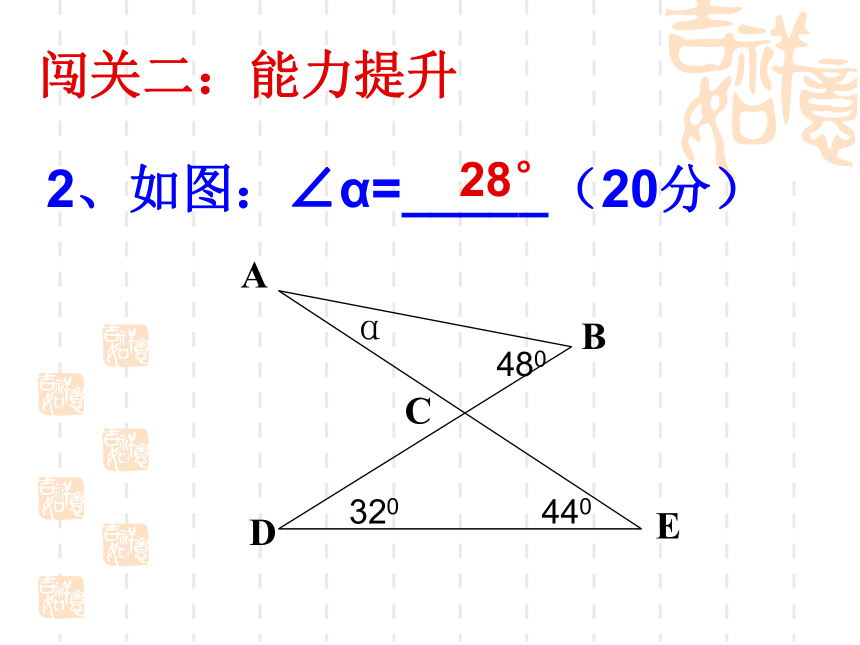
2、如图:∠α=_____(20分)
28°
A
E
D
B
C
闯关二:能力提升
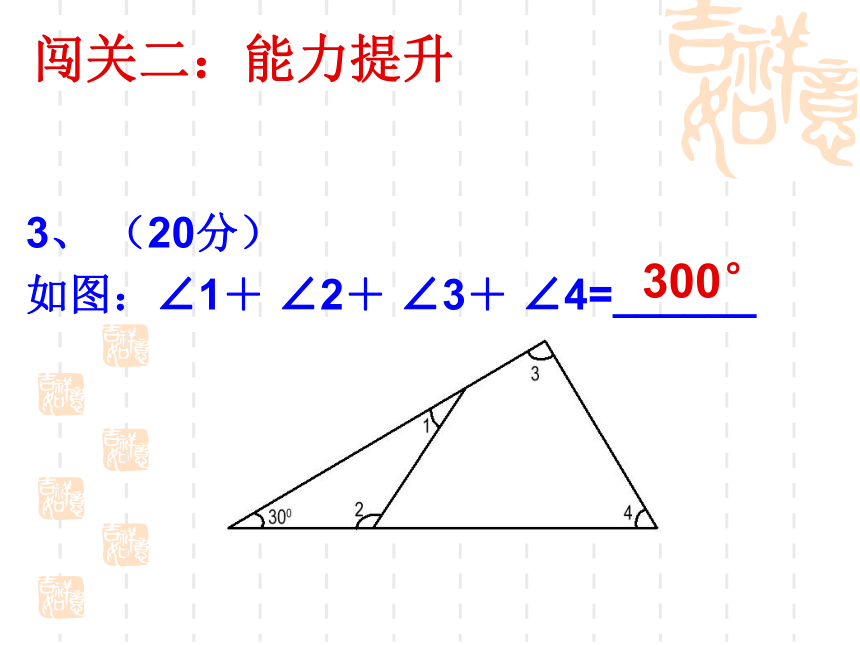
3、 (20分)
如图:∠1+ ∠2+ ∠3+ ∠4=______
300°
闯关二:能力提升
4、如图,直角三角形ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,
折痕为CD,则∠A′DB=( )(30分)
A、40° B、30° C、20° D、10°
D
闯关三:综合应用
我学习我收获:
1、三角形内角和定理的证明方法;
2、三角形内角和定理的应用;
布置作业:
必做题:P76. 1. 3.
选做题:证明三角形内角和定理的其他方法。
证明三角形内角和定理的其他方法
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
(
A
B
C
E
D
F
(
(
1
2
3
4
(
图5
)
A
E
)
1
2
B
C
D
图6
谢谢大家!
证法1:过A作EF∥BC,
∵ EF∥BC
∴∠B=∠2(两直线平行,内错角相等)
∠C=∠1(两直线平行,内错角相等)
又 ∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
F
2
1
E
C
B
A
注意:辅助线应该用虚线表示
证法2:延长BC到D,过C作CE∥BA,
∵CE∥BA
∴ ∠A=∠1(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
5、如图,BE平分∠ABD,CF平分∠ACD,
BE与CF交于点G,点∠BDC=140°,∠BGC=110°,则∠A的度数为( )
(30分)
A、70° B、75° C、80° D、85°
C
闯关三:综合应用
2如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F 的度数.
A
B
C
D
M
E
N
F
O
1
3
分析:三个三角形9个
内角之和为5400
所以∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F
=5400-1800=3600
∠1+ ∠2+ ∠3=1800
2
拓展延伸:
5、如图,△ABC中,AD⊥BC,AE平分∠BAC,
∠B=40°,∠C=60°,则∠DAE=__________
10°
已知△ABC中,∠ABC=∠C=2∠A ,BD⊥AC,求∠DBC的度数。
解:设∠A=x°,则∠C=∠ABC=2X0
∴x+2x+2x=180
解得:x=36
在△BDC中, ∵∠BDC=90°
∴∠DBC= 90°-72°
=18 °
∴∠C=72°
2、能力提升
三角形的内角
人教版数学七年级(下) 第七章 第三节
你有什么办法可以验证呢
三角形的内角和等于1800.
⑴度量法 ⑵拼图法
A
B
C
A
B
C
E
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°(等量代换)
∠EAC+∠C=180°
思路点拨:证明三个角的和为1800,常常将其转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
证法三:
闯关练习---分组抢答竞赛:
1、在老师示意开始抢答时,各小组举手抢答, 举手最多的小组获得答题权。
2、答对者小组获得相应的分数。答错者将答题权转给对方。
3、积分最高者为优胜组。
闯关一:基础过关
1、在△ABC中:若∠A=35°,∠ C =90°,
则 ∠B=______ (10分)
55°
2、如图:∠α=_____(20分)
28°
A
E
D
B
C
闯关二:能力提升
3、 (20分)
如图:∠1+ ∠2+ ∠3+ ∠4=______
300°
闯关二:能力提升
4、如图,直角三角形ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,
折痕为CD,则∠A′DB=( )(30分)
A、40° B、30° C、20° D、10°
D
闯关三:综合应用
我学习我收获:
1、三角形内角和定理的证明方法;
2、三角形内角和定理的应用;
布置作业:
必做题:P76. 1. 3.
选做题:证明三角形内角和定理的其他方法。
证明三角形内角和定理的其他方法
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
(
A
B
C
E
D
F
(
(
1
2
3
4
(
图5
)
A
E
)
1
2
B
C
D
图6
谢谢大家!
证法1:过A作EF∥BC,
∵ EF∥BC
∴∠B=∠2(两直线平行,内错角相等)
∠C=∠1(两直线平行,内错角相等)
又 ∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
F
2
1
E
C
B
A
注意:辅助线应该用虚线表示
证法2:延长BC到D,过C作CE∥BA,
∵CE∥BA
∴ ∠A=∠1(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
5、如图,BE平分∠ABD,CF平分∠ACD,
BE与CF交于点G,点∠BDC=140°,∠BGC=110°,则∠A的度数为( )
(30分)
A、70° B、75° C、80° D、85°
C
闯关三:综合应用
2如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F 的度数.
A
B
C
D
M
E
N
F
O
1
3
分析:三个三角形9个
内角之和为5400
所以∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F
=5400-1800=3600
∠1+ ∠2+ ∠3=1800
2
拓展延伸:
5、如图,△ABC中,AD⊥BC,AE平分∠BAC,
∠B=40°,∠C=60°,则∠DAE=__________
10°
已知△ABC中,∠ABC=∠C=2∠A ,BD⊥AC,求∠DBC的度数。
解:设∠A=x°,则∠C=∠ABC=2X0
∴x+2x+2x=180
解得:x=36
在△BDC中, ∵∠BDC=90°
∴∠DBC= 90°-72°
=18 °
∴∠C=72°
2、能力提升
