人教版六年级数学下册试题 一课一练《图形与几何--立体图形的表面积和体积》(含答案)
文档属性
| 名称 | 人教版六年级数学下册试题 一课一练《图形与几何--立体图形的表面积和体积》(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 369.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 15:36:07 | ||
图片预览



文档简介
《图形与几何--立体图形的表面积和体积》
一、选择题(共7小题,每小题2分,共14分)
1.一个大正方体如果拿出一个小方块后,它的表面积与原来的表面积比较
A.一样大
B.减少了
C.增大了
D.无法比较
2.一个长方体木块,长5分米,它有一组相对的面是正方形,其余4个面的面积和是40平方分米,则这个木块的体积是 立方分米.
A.20或50
B.20或48
C.20
3.如图,把一个高为4厘米的圆柱切成若干等份,拼成一个近似的长方体,表面积增加了40平方厘米.圆柱的侧面积是 平方厘米.
A.40
B.20
C.10
D.125.6
4.如图所示,一个铁锥完全浸没在水中.若铁锥一半露出水面,水面高度下降7厘米,若铁锥全部露出,水面高度共下降 厘米.
A.14
B.10.5
C.8
D.无法计算
5.把9个棱长是10厘米的正方体堆放在墙角(如图),露在外面的面积是 厘米.
A.1500
B.1600
C.1700
D.1800
6.小明拿了等底等高的圆锥和圆柱形容器各一个,他将圆柱形容器装满水后倒入圆锥形容器,当水全部倒满时,从圆锥形容器中溢出36.2毫升水.圆锥形容器内有水 毫升.
A.36.2
B.18.1
C.54.3
D.108.6
7.一个物体是由圆柱和圆锥黏合而成的(如图),如果把圆柱和圆锥重新分开,表面积就增加了,原来这个物体的体积是
A.
B.
C.
D.
二、填空题(共12小题,每小题2分,共24分)
1.一个正方体的棱长由5厘米变成8厘米,表面积增加了 平方厘米.
2.一个长方体的长、宽、高的比是,其中,长比高多4分米,它的体积是
立方分米.
3.一个长方体的长、宽、高分别是、、,这个长方体的占地面积最大是
,它的体积是
.
4.将一块长宽高分别为、、的长方体木块,分割成四个完全相同的小长方体木块,表面积最多增加 .
5.一个长方体木块长、宽、高分别是、、.如果用它锯成一个最大的正方体,体积比原来减少了 .
6.有一个正方体土坑,向下再挖深2米,它的表面积就增加64平方米,成为一个长方体土坑.这个长方体土坑的容积是
立方米.
7.把一根长的圆柱形木料截成2段后表面积比原木料增加了,这根木料的底面积是
,体积是
.
8.一个高的圆柱,沿着底面直径切成两个半圆柱,表面积增加,这个圆柱的底面直径是
.
9.一个棱长8分米的正方体水缸,水深6分米,如放入一块石头完全浸入水中,水溢出18升,则石头的体积是
.
10.如图有
个棱长为的正方体木箱堆放在墙角的形状,这些木箱的体积是
.
11.把一个圆柱体木料横切成两个圆柱(图,表面积增加了,纵切成两个半圆柱(图,则表面积增加了,原来这个圆柱的体积是
.
12.一根长方体木料,横截面是边长10厘米的正方形.从这根木料上截下6厘米长的一段,切削成一个最大的圆锥.圆锥的体积是
,约占截下这段长方体木料体积的
(百分号前面保留一位小数).
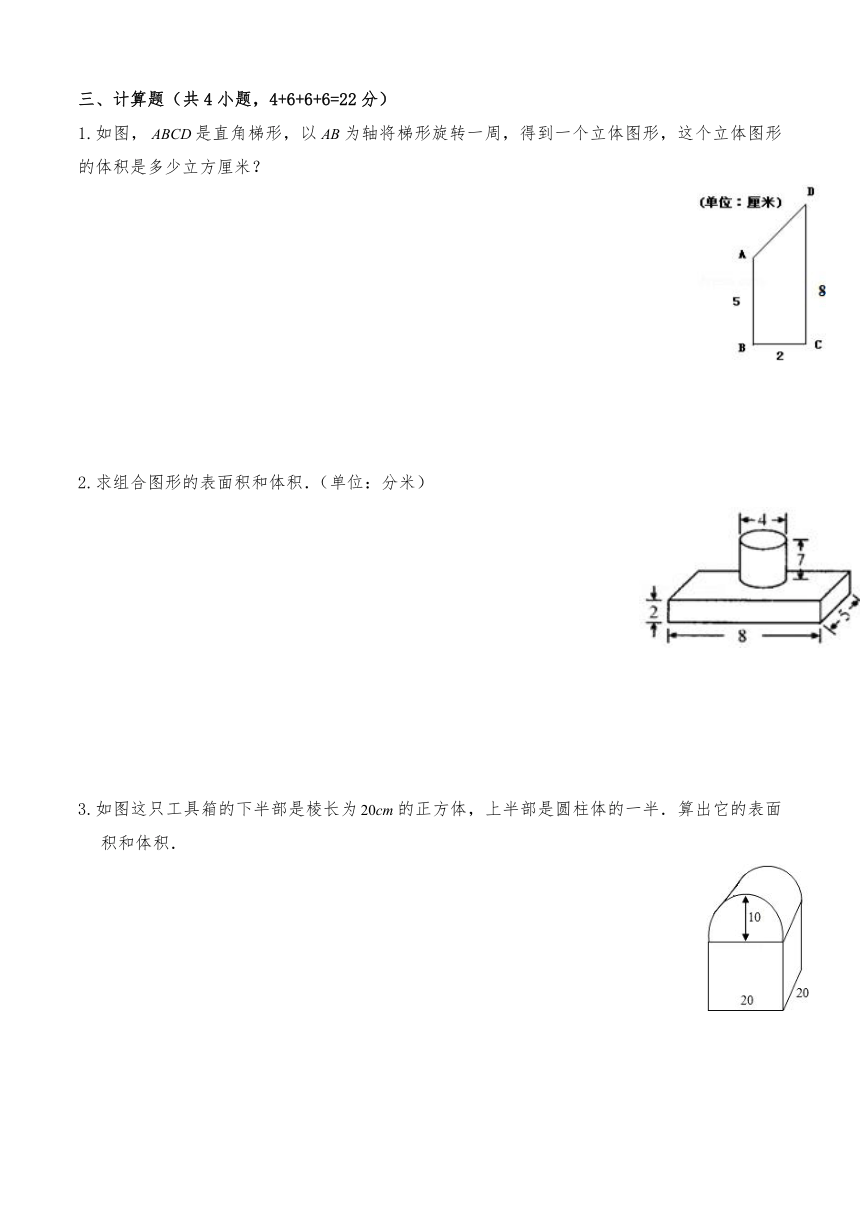
三、计算题(共4小题,4+6+6+6=22分)
1.如图,是直角梯形,以为轴将梯形旋转一周,得到一个立体图形,这个立体图形的体积是多少立方厘米?
2.求组合图形的表面积和体积.(单位:分米)
3.如图这只工具箱的下半部是棱长为的正方体,上半部是圆柱体的一半.算出它的表面积和体积.
4.如图,将三个高都是1米,底面半径分别是1.5米、1米、0.5米的3个圆柱体组成一个物体.
①求这个物体的体积?
②求这个物体的表面积?
四、解决问题(共8小题,每题5分,共40分)
1.把一个长、宽、高的长方体木块锯成两个相同的小长方体木块.这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了多少平方厘米?(请你将几种情况都写出来)
2.把两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体,拼成一个大长方体,这个大长方体的表面积最少是多少?
3.一个长方体木块,从下部和上部分别截去高为3厘米和2厘米的长方体后,便成为一个正方体,表面积减少了120平方厘米,原来长方体的体积是多少立方厘米?
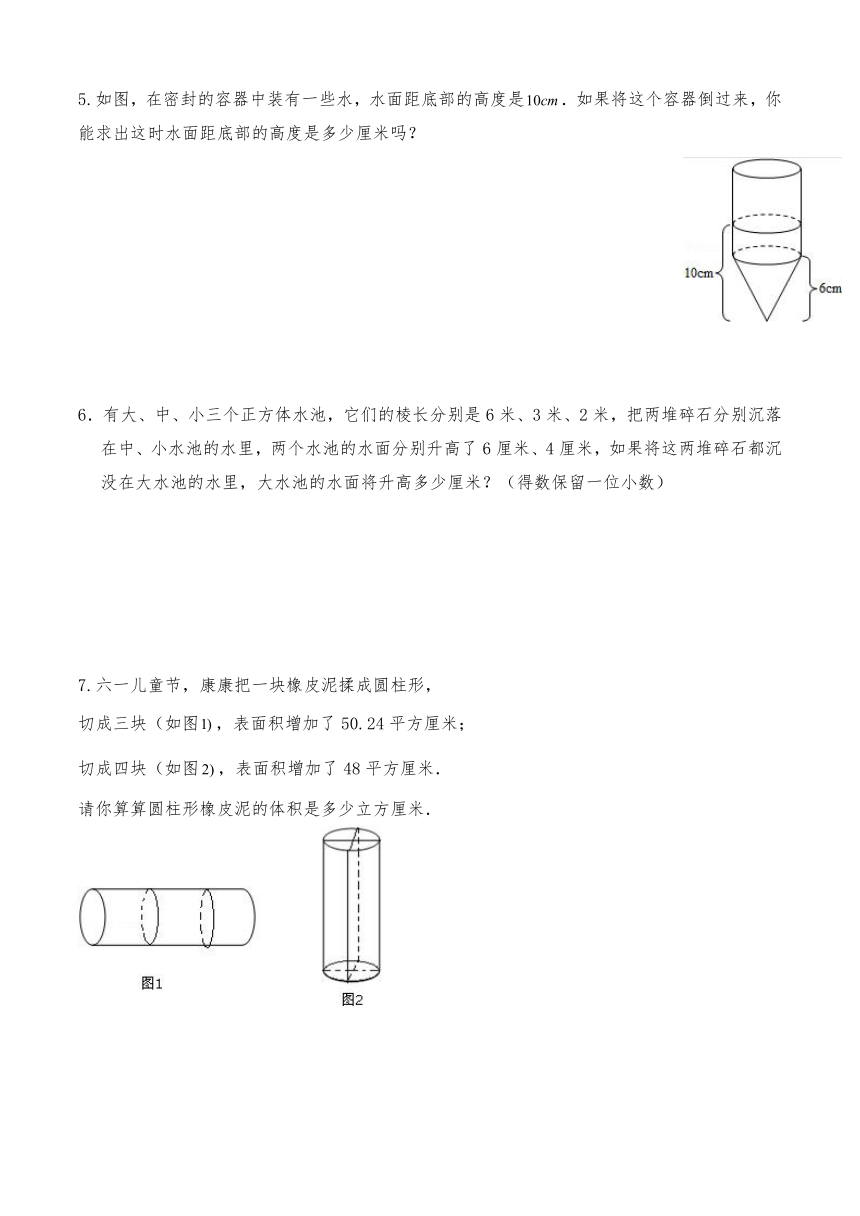
5.如图,在密封的容器中装有一些水,水面距底部的高度是.如果将这个容器倒过来,你能求出这时水面距底部的高度是多少厘米吗?
6.有大、中、小三个正方体水池,它们的棱长分别是6米、3米、2米,把两堆碎石分别沉落在中、小水池的水里,两个水池的水面分别升高了6厘米、4厘米,如果将这两堆碎石都沉没在大水池的水里,大水池的水面将升高多少厘米?(得数保留一位小数)
7.六一儿童节,康康把一块橡皮泥揉成圆柱形,
切成三块(如图,表面积增加了50.24平方厘米;
切成四块(如图,表面积增加了48平方厘米.
请你算算圆柱形橡皮泥的体积是多少立方厘米.
8.一个酸奶瓶(如图),它的瓶身呈圆柱形(不包括瓶颈),容积是32.4立方厘米.当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?
9.一个长方体水箱,高40厘米,底面是边长为12厘米的正方形(厚度忽略不计),水箱内有25厘米深的水,现将一根长50厘米的钢柱垂直地插入水箱中,使钢柱的底面与水箱的底面重合.已知长方体钢柱横截面是边长为4厘米的正方形,则水面会上升多少厘米?
答案
一、选择题
1..2..3..4..5..6..7..
二、填空题
1.234.
2.48.
3.48、192.
4.72.
5.20.
6.640.
7.0.4;0.8.
8.9.
9.146.
10.5个,40000.
11.75.36.
12.157;26.2.
三、计算题
1.解:如下图:
(立方厘米),
答:这个立体图形的体积是87.92立方厘米.
2.解:
(平方分米);
(立方分米);
答:它的表面积是219.92平方分米,体积是167.92立方分米.
3.解:表面积:
,
,
,
(平方厘米);
体积:
,
,
,
(立方厘米);
答:它的表面积是2942平方厘米,体积是11140立方厘米.
4.解:(1),
,
,
(立方米),
答:这个物体的体积是10.99立方米.
(2)大圆柱的表面积:,
,
(平方米),
中圆柱侧面积:(平方米),
小圆柱侧面积:(平方米),
这个物体的表面积:(平方米);
答:这个物体的表面积是32.97平方米.
四、解决问题
1.解:
(1)
(平方厘米)
答:这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了144平方厘米.
(2)
(平方厘米)
答:这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了216平方厘米.
(3)
(平方厘米)
答:这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了108平方厘米.
2.解:,
,
,
(平方厘米);
答:大长方体的表面积最小是382平方厘米.
3.解:(厘米);
(立方厘米);
答:原来长方体的体积是396立方厘米.
4.解:高6厘米的圆锥容器中水倒入等底的圆柱容器中高是(厘米)
(厘米),
答:如果将这个容器倒过来,这时水面距底部的高度是6厘米.
5.解:6米厘米
3米厘米
2米厘米
放中池里碎石的体积:(立方厘米)
放小池里碎石的体积:(立方厘米)
两堆碎石总体积:(立方厘米)
大水池的水面升高:(厘米)
答:大水池的水面将升高大约1.9厘米.
6.解:(平方厘米);
假设圆柱的底面半径是,则,
所以,所以(厘米);
圆柱的高:
(厘米)
体积为:
(立方厘米)
答:圆柱形橡皮泥的体积是37.68立方厘米.
7.解:(厘米),
(立方厘米),
答:瓶内酸奶体积是25.92立方厘米.
8.解:设放入钢柱后水箱内的水深为厘米,根据题意可得:
(厘米)
答:水面会上升3.125厘米.
一、选择题(共7小题,每小题2分,共14分)
1.一个大正方体如果拿出一个小方块后,它的表面积与原来的表面积比较
A.一样大
B.减少了
C.增大了
D.无法比较
2.一个长方体木块,长5分米,它有一组相对的面是正方形,其余4个面的面积和是40平方分米,则这个木块的体积是 立方分米.
A.20或50
B.20或48
C.20
3.如图,把一个高为4厘米的圆柱切成若干等份,拼成一个近似的长方体,表面积增加了40平方厘米.圆柱的侧面积是 平方厘米.
A.40
B.20
C.10
D.125.6
4.如图所示,一个铁锥完全浸没在水中.若铁锥一半露出水面,水面高度下降7厘米,若铁锥全部露出,水面高度共下降 厘米.
A.14
B.10.5
C.8
D.无法计算
5.把9个棱长是10厘米的正方体堆放在墙角(如图),露在外面的面积是 厘米.
A.1500
B.1600
C.1700
D.1800
6.小明拿了等底等高的圆锥和圆柱形容器各一个,他将圆柱形容器装满水后倒入圆锥形容器,当水全部倒满时,从圆锥形容器中溢出36.2毫升水.圆锥形容器内有水 毫升.
A.36.2
B.18.1
C.54.3
D.108.6
7.一个物体是由圆柱和圆锥黏合而成的(如图),如果把圆柱和圆锥重新分开,表面积就增加了,原来这个物体的体积是
A.
B.
C.
D.
二、填空题(共12小题,每小题2分,共24分)
1.一个正方体的棱长由5厘米变成8厘米,表面积增加了 平方厘米.
2.一个长方体的长、宽、高的比是,其中,长比高多4分米,它的体积是
立方分米.
3.一个长方体的长、宽、高分别是、、,这个长方体的占地面积最大是
,它的体积是
.
4.将一块长宽高分别为、、的长方体木块,分割成四个完全相同的小长方体木块,表面积最多增加 .
5.一个长方体木块长、宽、高分别是、、.如果用它锯成一个最大的正方体,体积比原来减少了 .
6.有一个正方体土坑,向下再挖深2米,它的表面积就增加64平方米,成为一个长方体土坑.这个长方体土坑的容积是
立方米.
7.把一根长的圆柱形木料截成2段后表面积比原木料增加了,这根木料的底面积是
,体积是
.
8.一个高的圆柱,沿着底面直径切成两个半圆柱,表面积增加,这个圆柱的底面直径是
.
9.一个棱长8分米的正方体水缸,水深6分米,如放入一块石头完全浸入水中,水溢出18升,则石头的体积是
.
10.如图有
个棱长为的正方体木箱堆放在墙角的形状,这些木箱的体积是
.
11.把一个圆柱体木料横切成两个圆柱(图,表面积增加了,纵切成两个半圆柱(图,则表面积增加了,原来这个圆柱的体积是
.
12.一根长方体木料,横截面是边长10厘米的正方形.从这根木料上截下6厘米长的一段,切削成一个最大的圆锥.圆锥的体积是
,约占截下这段长方体木料体积的
(百分号前面保留一位小数).
三、计算题(共4小题,4+6+6+6=22分)
1.如图,是直角梯形,以为轴将梯形旋转一周,得到一个立体图形,这个立体图形的体积是多少立方厘米?
2.求组合图形的表面积和体积.(单位:分米)
3.如图这只工具箱的下半部是棱长为的正方体,上半部是圆柱体的一半.算出它的表面积和体积.
4.如图,将三个高都是1米,底面半径分别是1.5米、1米、0.5米的3个圆柱体组成一个物体.
①求这个物体的体积?
②求这个物体的表面积?
四、解决问题(共8小题,每题5分,共40分)
1.把一个长、宽、高的长方体木块锯成两个相同的小长方体木块.这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了多少平方厘米?(请你将几种情况都写出来)
2.把两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体,拼成一个大长方体,这个大长方体的表面积最少是多少?
3.一个长方体木块,从下部和上部分别截去高为3厘米和2厘米的长方体后,便成为一个正方体,表面积减少了120平方厘米,原来长方体的体积是多少立方厘米?
5.如图,在密封的容器中装有一些水,水面距底部的高度是.如果将这个容器倒过来,你能求出这时水面距底部的高度是多少厘米吗?
6.有大、中、小三个正方体水池,它们的棱长分别是6米、3米、2米,把两堆碎石分别沉落在中、小水池的水里,两个水池的水面分别升高了6厘米、4厘米,如果将这两堆碎石都沉没在大水池的水里,大水池的水面将升高多少厘米?(得数保留一位小数)
7.六一儿童节,康康把一块橡皮泥揉成圆柱形,
切成三块(如图,表面积增加了50.24平方厘米;
切成四块(如图,表面积增加了48平方厘米.
请你算算圆柱形橡皮泥的体积是多少立方厘米.
8.一个酸奶瓶(如图),它的瓶身呈圆柱形(不包括瓶颈),容积是32.4立方厘米.当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?
9.一个长方体水箱,高40厘米,底面是边长为12厘米的正方形(厚度忽略不计),水箱内有25厘米深的水,现将一根长50厘米的钢柱垂直地插入水箱中,使钢柱的底面与水箱的底面重合.已知长方体钢柱横截面是边长为4厘米的正方形,则水面会上升多少厘米?
答案
一、选择题
1..2..3..4..5..6..7..
二、填空题
1.234.
2.48.
3.48、192.
4.72.
5.20.
6.640.
7.0.4;0.8.
8.9.
9.146.
10.5个,40000.
11.75.36.
12.157;26.2.
三、计算题
1.解:如下图:
(立方厘米),
答:这个立体图形的体积是87.92立方厘米.
2.解:
(平方分米);
(立方分米);
答:它的表面积是219.92平方分米,体积是167.92立方分米.
3.解:表面积:
,
,
,
(平方厘米);
体积:
,
,
,
(立方厘米);
答:它的表面积是2942平方厘米,体积是11140立方厘米.
4.解:(1),
,
,
(立方米),
答:这个物体的体积是10.99立方米.
(2)大圆柱的表面积:,
,
(平方米),
中圆柱侧面积:(平方米),
小圆柱侧面积:(平方米),
这个物体的表面积:(平方米);
答:这个物体的表面积是32.97平方米.
四、解决问题
1.解:
(1)
(平方厘米)
答:这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了144平方厘米.
(2)
(平方厘米)
答:这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了216平方厘米.
(3)
(平方厘米)
答:这两个小长方体木块的表面积之和比原来长方体木块的表面积增加了108平方厘米.
2.解:,
,
,
(平方厘米);
答:大长方体的表面积最小是382平方厘米.
3.解:(厘米);
(立方厘米);
答:原来长方体的体积是396立方厘米.
4.解:高6厘米的圆锥容器中水倒入等底的圆柱容器中高是(厘米)
(厘米),
答:如果将这个容器倒过来,这时水面距底部的高度是6厘米.
5.解:6米厘米
3米厘米
2米厘米
放中池里碎石的体积:(立方厘米)
放小池里碎石的体积:(立方厘米)
两堆碎石总体积:(立方厘米)
大水池的水面升高:(厘米)
答:大水池的水面将升高大约1.9厘米.
6.解:(平方厘米);
假设圆柱的底面半径是,则,
所以,所以(厘米);
圆柱的高:
(厘米)
体积为:
(立方厘米)
答:圆柱形橡皮泥的体积是37.68立方厘米.
7.解:(厘米),
(立方厘米),
答:瓶内酸奶体积是25.92立方厘米.
8.解:设放入钢柱后水箱内的水深为厘米,根据题意可得:
(厘米)
答:水面会上升3.125厘米.
