人教版六年级数学下册试题 一课一练《图形与几何-立体图形的认识与测量(二)》(含答案)
文档属性
| 名称 | 人教版六年级数学下册试题 一课一练《图形与几何-立体图形的认识与测量(二)》(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 463.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 15:38:24 | ||
图片预览



文档简介
《图形与几何-立体图形的认识与测量(二)》
一、选择题(共8小题,每小题2分,共16分)
1.把一个正方体加工成一个最大的圆柱体,下面的说法正确的是
A.正方体的体积等于圆柱体的体积
B.正方体的表面积等于圆柱体的表面积
C.正方体的棱长等于圆柱的高
D.正方体的棱长等于圆柱的底面周长的一半
2.下面的三句话中, 是错误的.
A.圆锥的顶点到底面圆心的距离是圆锥的高
B.一个圆柱侧面展开图是正方形,这个圆柱的底面周长和高相等
C.三角形的底和高成反比例
3.一个圆柱的侧面展开图是一个正方形,这个圆柱的高与底面半径的比值是
A.
B.
C.
4.圆柱、圆锥、正方体和长方体的底面周长和高相等, 的体积最大.
A.圆柱
B.圆锥
C.正方体
D.长方体
5.把一个圆柱体沿半径和高平均切成若干份以后,重新拼插成一个近似长方体,原来圆柱体的侧面积是.长方体的表面积比圆柱体增加
A.
B.
C.
D.
6.一个底面积是的圆柱,斜着截去了一段后,剩下的图形如图.截后剩下的图形的体积是 .
A.140
B.180
C.220
D.360
7.把一个圆柱削成一个与它等底等高的圆锥,削去的体积是90立方厘米,这个圆柱的体积是多少立方厘米?列式正确的是
A.
B.
C.
D.
8.一个底面半径是10厘米的圆锥,它的高如果增加3厘米,它的体积将会增加 立方厘米.
A.3.14
B.78.5
C.314
D.7.85
二、填空题
1.一个边长3厘米的正方形,以它的一条边为轴,旋转后的图形是
,这个旋转后的图形的体积是
立方厘米.
2.有一张长方体铁皮(如图),剪下图中两个圆及一块长方形,正好可以做成一个圆柱体,这个圆柱体的底面半径为10厘米,那么圆柱的底面积是
平方厘米,体积是
立方厘米.
3.(单位:以直角三角形的长直角边为轴旋转一周(如图)得到几何体是 ,体积是
.
4.两个完全相同的圆柱能拼成一个长12厘米的圆柱,但表面积比原来减少了25.12平方厘米,原来一个圆柱体的体积是
立方厘米.若将原来一个圆柱体削成一个最大的圆锥,则体积会减少 立方厘米.
5.一个直角三角形的三条边长分别是、和,若以直角边为轴旋转一圈,旋转一圈形成的图形体积是
立方厘米.取
6.把一个圆柱木料削成一个最大的圆锥,体积减少了24立方厘米,原来圆柱的底面积是9平方厘米,削成的圆锥的高是 厘米.
7.底面积是,高是的圆锥的体积是
,与它等底等高的圆柱的体积是
.
8.一个圆柱和一个圆锥等底等高,如果圆柱比圆锥的体积多,则圆柱的体积是
,圆锥的体积是
.
9.如图,把一个底面半径为的圆柱,拼成一个近似的长方体,长方体的表面积比圆柱增加了,圆柱的高是 ,体积是
.
10.一个棱长是的正方体容器装满了水后,倒入一个底面积是的圆锥形容器正好装满,这个圆锥的高是 .
11.将一段底面直径和高都是10厘米的圆木沿直径切割成两个半圆柱,表面积之和比原来增加了 平方厘米.
12.图中一个小球的体积是
立方厘米,一个大球的体积是
立方厘米.
三、计算题(共3小题,6+6+8=20分)
1.求如图图形的表面积.(单位:厘米)
2.如图是一个直角三角形.边上的高是多少厘米?(请先在图中画出高,并计算)再算一算,以为轴旋转一周形成的立体图形的体积是多少立方厘米?
3.如图所示,某机器零件中间是一个棱长为2厘米的正方体,两边各是圆柱体的一半,求这个零件的表面积和体积.
四、解决问题(共7小题,第24题、第25题每题5分,其余每题6分,共40分)
1.用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米.扎这个盒子至少用去塑料绳多少厘米?在它的整个侧面贴上商标和说明,这部分的面积是多少平方厘米?
2.如图是用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个直径2米的半圆.
(1)这个大棚的种植面积是多少平方米?
(2)覆盖在这个大棚上的塑料薄膜约有多少平方米?
(3)大棚内的空间大约有多大?
3.一个底面直径是4厘米的圆锥如图,从顶点沿着高将它切成两半后,表面积增加了24平方分米.这个圆锥的体积是多少平方厘米?
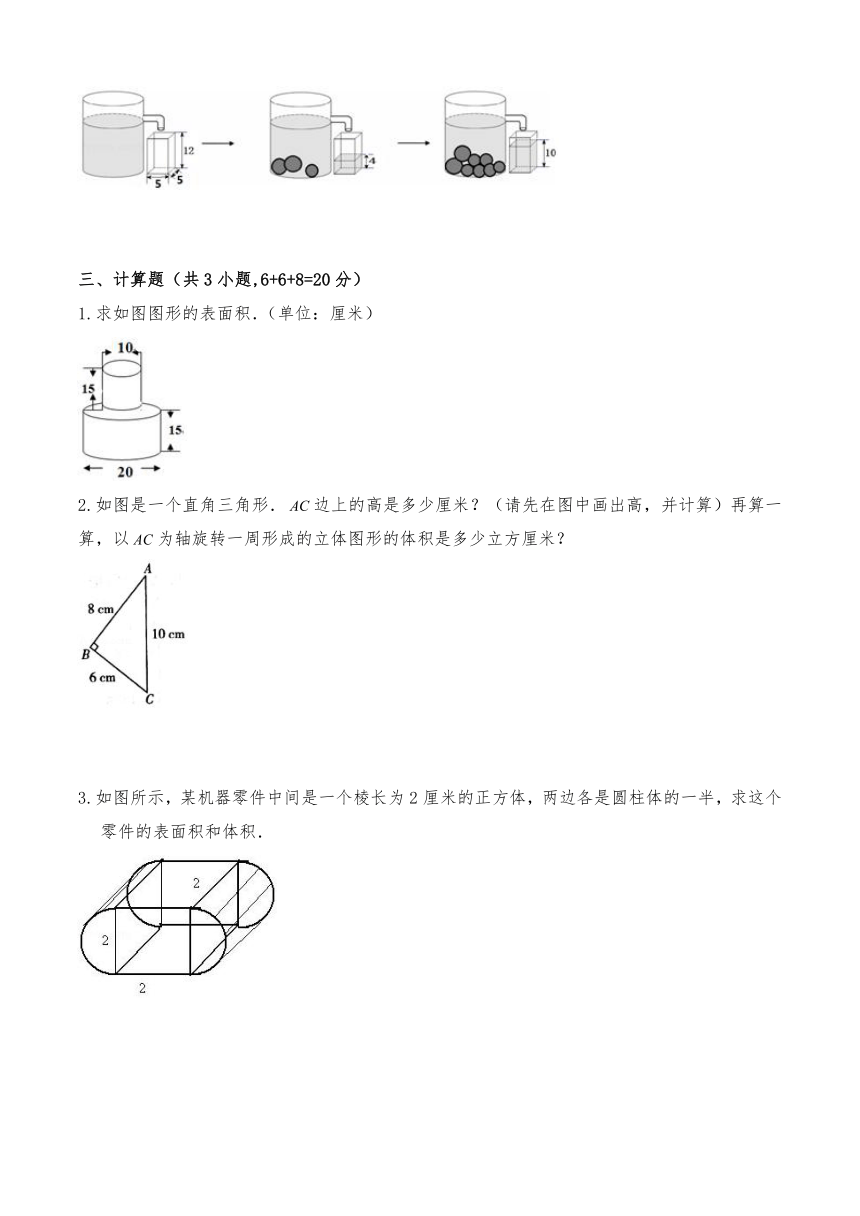
4.有一个高8厘米,容量为50毫升的圆形容器,里面装满了水,现把长16厘米的圆柱垂直放入,使的底和的底面接触,这时一部分水从容器中溢出,当把从拿走后,中的水的高度只有6厘米,求圆柱体的体积是多少?
5.一个圆柱形水桶,底面半径为,里面盛有深的水,现将一个底面周长为的圆锥形铁块完全浸没在水中,水面上升了.圆锥形铁块的高度是多少?取
6.一个装满水的矿泉水瓶,内直径是8厘米.小亮喝了一些,水的高度还有12厘米,把瓶盖拧紧后倒置放平无水部分高10厘米.小亮喝了多少水?
7.一个圆柱形木块切成四块(如图,表面积增加48平方厘米;切成三块(如图,表面积增加了50.24平方厘米.若削成一个最大的圆锥体(如图,体积减少了多少立方厘米?
答案
一、选一选
1..2..3..4..5..6..7..8..
二、填空题
1.圆柱;84.78.
2.314、6280.
3.圆锥体,37.68.
4.75.36;50.24.
5.37.68、50.24.
6.4.
7.50、150.
8.114、38.
9.5、251.2.
10.36分米.
11.200.
12.30,35.
三、计算题
1.解:
(平方厘米)
答:这个图形的表面积是2041平方厘米.
2.解:边上的高:
如图:
(厘米)
(立方厘米)
答:以为轴旋转一周形成的立体图形的体积是241.152立方厘米.
3.解:
(平方厘米);
(立方厘米);
答:这个零件的表面积是28.56平方厘米,体积是14.28立方厘米.
四、解决问题
1.解:(1),
,
(厘米),
面积:,
,
(平方厘米);
答:扎这个盒子至少用去塑料绳545厘米,在它的整个侧面贴上商标和说明,这部分的面积是2355平方厘米.
2.解:(1)(平方米),
答:这个大棚的种植面积是30平方米.
(2),
,
(平方米),
答:覆盖在这个大棚上的塑料薄膜约有50.24平方米.
(2),
,
(立方米),
答:大棚的空间是23.55立方米.
3.解:24平方分米平方厘米
(厘米)
(立方厘米)
答:这个圆锥的体积是2512立方厘米.
4.解:圆形容器的底面积:
(平方厘米);
溢出水的体积,即放入容器的圆柱的体积:
,
,
(毫升);
圆柱体的体积是:
,
,
(立方厘米);
答:圆柱体的体积是25立方厘米.
5.解:设圆锥形铁块的高是厘米
,
,
;
答:圆锥形铁块的高是60厘米.
6.解:
(立方厘米)
(毫升)
答:小亮喝了502.4毫升水.
7.解:(平方厘米);
,因为;
所以这个圆柱的底面半径是2厘米;
(厘米);
(立方厘米)
答:体积减少了25.12立方厘米.
一、选择题(共8小题,每小题2分,共16分)
1.把一个正方体加工成一个最大的圆柱体,下面的说法正确的是
A.正方体的体积等于圆柱体的体积
B.正方体的表面积等于圆柱体的表面积
C.正方体的棱长等于圆柱的高
D.正方体的棱长等于圆柱的底面周长的一半
2.下面的三句话中, 是错误的.
A.圆锥的顶点到底面圆心的距离是圆锥的高
B.一个圆柱侧面展开图是正方形,这个圆柱的底面周长和高相等
C.三角形的底和高成反比例
3.一个圆柱的侧面展开图是一个正方形,这个圆柱的高与底面半径的比值是
A.
B.
C.
4.圆柱、圆锥、正方体和长方体的底面周长和高相等, 的体积最大.
A.圆柱
B.圆锥
C.正方体
D.长方体
5.把一个圆柱体沿半径和高平均切成若干份以后,重新拼插成一个近似长方体,原来圆柱体的侧面积是.长方体的表面积比圆柱体增加
A.
B.
C.
D.
6.一个底面积是的圆柱,斜着截去了一段后,剩下的图形如图.截后剩下的图形的体积是 .
A.140
B.180
C.220
D.360
7.把一个圆柱削成一个与它等底等高的圆锥,削去的体积是90立方厘米,这个圆柱的体积是多少立方厘米?列式正确的是
A.
B.
C.
D.
8.一个底面半径是10厘米的圆锥,它的高如果增加3厘米,它的体积将会增加 立方厘米.
A.3.14
B.78.5
C.314
D.7.85
二、填空题
1.一个边长3厘米的正方形,以它的一条边为轴,旋转后的图形是
,这个旋转后的图形的体积是
立方厘米.
2.有一张长方体铁皮(如图),剪下图中两个圆及一块长方形,正好可以做成一个圆柱体,这个圆柱体的底面半径为10厘米,那么圆柱的底面积是
平方厘米,体积是
立方厘米.
3.(单位:以直角三角形的长直角边为轴旋转一周(如图)得到几何体是 ,体积是
.
4.两个完全相同的圆柱能拼成一个长12厘米的圆柱,但表面积比原来减少了25.12平方厘米,原来一个圆柱体的体积是
立方厘米.若将原来一个圆柱体削成一个最大的圆锥,则体积会减少 立方厘米.
5.一个直角三角形的三条边长分别是、和,若以直角边为轴旋转一圈,旋转一圈形成的图形体积是
立方厘米.取
6.把一个圆柱木料削成一个最大的圆锥,体积减少了24立方厘米,原来圆柱的底面积是9平方厘米,削成的圆锥的高是 厘米.
7.底面积是,高是的圆锥的体积是
,与它等底等高的圆柱的体积是
.
8.一个圆柱和一个圆锥等底等高,如果圆柱比圆锥的体积多,则圆柱的体积是
,圆锥的体积是
.
9.如图,把一个底面半径为的圆柱,拼成一个近似的长方体,长方体的表面积比圆柱增加了,圆柱的高是 ,体积是
.
10.一个棱长是的正方体容器装满了水后,倒入一个底面积是的圆锥形容器正好装满,这个圆锥的高是 .
11.将一段底面直径和高都是10厘米的圆木沿直径切割成两个半圆柱,表面积之和比原来增加了 平方厘米.
12.图中一个小球的体积是
立方厘米,一个大球的体积是
立方厘米.
三、计算题(共3小题,6+6+8=20分)
1.求如图图形的表面积.(单位:厘米)
2.如图是一个直角三角形.边上的高是多少厘米?(请先在图中画出高,并计算)再算一算,以为轴旋转一周形成的立体图形的体积是多少立方厘米?
3.如图所示,某机器零件中间是一个棱长为2厘米的正方体,两边各是圆柱体的一半,求这个零件的表面积和体积.
四、解决问题(共7小题,第24题、第25题每题5分,其余每题6分,共40分)
1.用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米.扎这个盒子至少用去塑料绳多少厘米?在它的整个侧面贴上商标和说明,这部分的面积是多少平方厘米?
2.如图是用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个直径2米的半圆.
(1)这个大棚的种植面积是多少平方米?
(2)覆盖在这个大棚上的塑料薄膜约有多少平方米?
(3)大棚内的空间大约有多大?
3.一个底面直径是4厘米的圆锥如图,从顶点沿着高将它切成两半后,表面积增加了24平方分米.这个圆锥的体积是多少平方厘米?
4.有一个高8厘米,容量为50毫升的圆形容器,里面装满了水,现把长16厘米的圆柱垂直放入,使的底和的底面接触,这时一部分水从容器中溢出,当把从拿走后,中的水的高度只有6厘米,求圆柱体的体积是多少?
5.一个圆柱形水桶,底面半径为,里面盛有深的水,现将一个底面周长为的圆锥形铁块完全浸没在水中,水面上升了.圆锥形铁块的高度是多少?取
6.一个装满水的矿泉水瓶,内直径是8厘米.小亮喝了一些,水的高度还有12厘米,把瓶盖拧紧后倒置放平无水部分高10厘米.小亮喝了多少水?
7.一个圆柱形木块切成四块(如图,表面积增加48平方厘米;切成三块(如图,表面积增加了50.24平方厘米.若削成一个最大的圆锥体(如图,体积减少了多少立方厘米?
答案
一、选一选
1..2..3..4..5..6..7..8..
二、填空题
1.圆柱;84.78.
2.314、6280.
3.圆锥体,37.68.
4.75.36;50.24.
5.37.68、50.24.
6.4.
7.50、150.
8.114、38.
9.5、251.2.
10.36分米.
11.200.
12.30,35.
三、计算题
1.解:
(平方厘米)
答:这个图形的表面积是2041平方厘米.
2.解:边上的高:
如图:
(厘米)
(立方厘米)
答:以为轴旋转一周形成的立体图形的体积是241.152立方厘米.
3.解:
(平方厘米);
(立方厘米);
答:这个零件的表面积是28.56平方厘米,体积是14.28立方厘米.
四、解决问题
1.解:(1),
,
(厘米),
面积:,
,
(平方厘米);
答:扎这个盒子至少用去塑料绳545厘米,在它的整个侧面贴上商标和说明,这部分的面积是2355平方厘米.
2.解:(1)(平方米),
答:这个大棚的种植面积是30平方米.
(2),
,
(平方米),
答:覆盖在这个大棚上的塑料薄膜约有50.24平方米.
(2),
,
(立方米),
答:大棚的空间是23.55立方米.
3.解:24平方分米平方厘米
(厘米)
(立方厘米)
答:这个圆锥的体积是2512立方厘米.
4.解:圆形容器的底面积:
(平方厘米);
溢出水的体积,即放入容器的圆柱的体积:
,
,
(毫升);
圆柱体的体积是:
,
,
(立方厘米);
答:圆柱体的体积是25立方厘米.
5.解:设圆锥形铁块的高是厘米
,
,
;
答:圆锥形铁块的高是60厘米.
6.解:
(立方厘米)
(毫升)
答:小亮喝了502.4毫升水.
7.解:(平方厘米);
,因为;
所以这个圆柱的底面半径是2厘米;
(厘米);
(立方厘米)
答:体积减少了25.12立方厘米.
