人教版六年级数学下册试题 一课一练《图形与几何-平面图形的认识与测量(一)》(含答案)
文档属性
| 名称 | 人教版六年级数学下册试题 一课一练《图形与几何-平面图形的认识与测量(一)》(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 403.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 00:00:00 | ||
图片预览



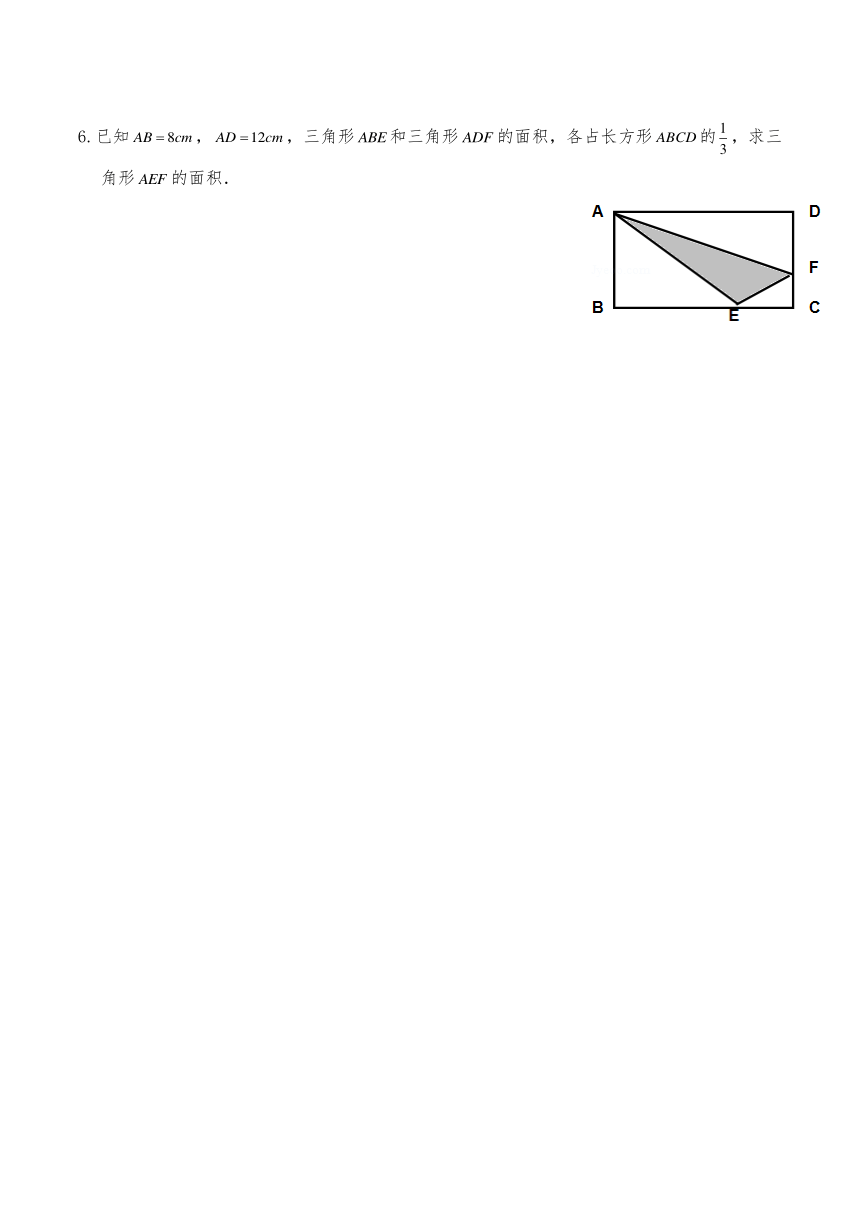
文档简介
《图形与几何-平面图形的认识与测量(一)》
一、选一选(共8小题,每小题2分,共16分)
1.下列图形中,最具有稳定性、不易变形的特性的是
A.三角形
B.平行四边形
C.正方形
D.长方形
2.用一副三角板,不能拼出 的角.
A.15度
B.20度
C.135度
D.150度
3.按记号折后能围成一个长方形的铁丝是
A.
B.
C.
4.下面能围成等腰三角形的一组小棒是
A.,,
B.,,
C.,,
5.如图,如果,那么
A.
B.
C.
6.把一个等边三角形沿其中一条高剪开,分成两个直角三角形,其中一个直角三角形的两个锐角分别是
A.和
B.和
C.和
7.一个平行四边形和一个三角形的面积相等,已知平行四边形的底是24厘米,高14厘米,三角形的底是42厘米,三角形的高是
A.336厘米
B.32厘米
C.4厘米
D.16厘米
8.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长
A.24厘米
B.12厘米
C.18厘米
D.36厘米
二、填空题(共11小题,每小题2分,共22分)
1.3时整,时针与分针所组成的角是
角,4时整,时针与分针所组成的角是
角.
2.图有
条线段,
条直线,
条射线.
3.在一个三角形中,一个角是,另一个角是,第三个角是
度,这个三角形是
三角形.
4.如果两条直线相交的夹角是,那么这两条直线相互 ,其中一条是另一条的 ,它们的交点叫做 .
5.等腰三角形中不相等的两角之比是,则它的顶角是
度或
度.
6.一个等腰三角形,两条边比是,其中最短边长度是,则这个三角形的周长是 厘米.
7.以点为顶点画一个15度的角,再以点为顶点画一个125度的角.组成三角形的另一个角是
度.
8.一块长方形的纸板,长32厘米,宽24厘米,从这块纸板上剪下一个尽可能大的正方形纸板.这块正方形纸板的面积是原来长方形纸板的 .
9.一个平行四边形的面积是72平方厘米,与它等底等高的三角形的底是18厘米.则三角形的高是 厘米.
10.一块梯形菜地,上底是45米,下底是63米,高是25米,如果每100平方米施化肥0.85千克,这块地共施化肥 千克.(得数保留两位小数)
11.平行四边形的一边长为,相邻的另一边比它的多,则这个平行四边形的周长为 .
三.计算题(共4小题,6+9+4+4=23分)
1.求图中指定角的度数.(共2小题,每小题3分,共6分)
(1)求和的度数.
(2)求的度数.
2.计算下面各图形的周长.(共3小题,每小题3分,共9分)
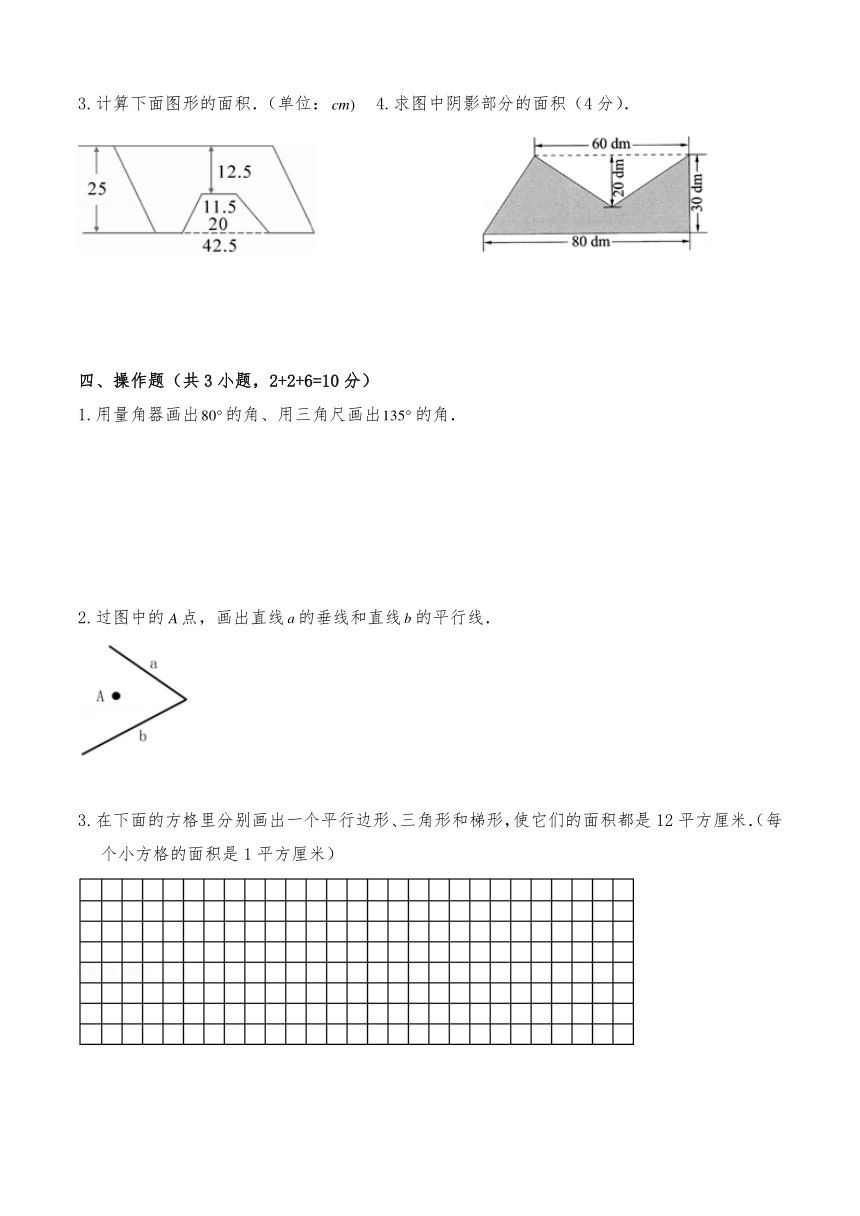
3.计算下面图形的面积.(单位:
4.求图中阴影部分的面积(4分).
四、操作题(共3小题,2+2+6=10分)
1.用量角器画出的角、用三角尺画出的角.
2.过图中的点,画出直线的垂线和直线的平行线.
3.在下面的方格里分别画出一个平行边形、三角形和梯形,使它们的面积都是12平方厘米.(每个小方格的面积是1平方厘米)
五、解决问题(共6小题,第27题4分,其余每题5分,共29分)
1.如图一张长方形纸,把它的一角折叠过来,已知你能求出等于多少度吗?
2.某游泳馆有大小两个游泳池,小聪来到游泳馆游泳,这时游泳池中的游泳人数情况如图.根据当时的情况,管理员应将小聪安排在哪个游泳池中?说说你的理由.
3.甲、乙、丙三个平行四边形的底之比是,高之比是,已知三个平行四边形的面积是140平方分米,那么,甲、乙、丙三个平行四边形的面积各是多少?
4.平行四边形的周长是102厘米,以为底时,高为14厘米;以为底时,高为20厘米,求平行四边形的面积.
5.有一个直角梯形,上底是下底的,如果下底减少8厘米,正好变成一个正方形,原来这个梯形的面积是多少?
6.已知,,三角形和三角形的面积,各占长方形的,求三角形的面积.
答案
一、选择题
1..2..3..4..5..6..7..8..
二、填空题
1.直,钝.
2.3,1,6.
3.:75,锐角.
4.垂直;垂线;垂足.
5.30、100.
6.50.
7.40.
8..
9.4.
10.11.48.
11.32.
三、计算题
1.解:(1)因为
所以
因为
所以.
(2)因为
所以
2.解:(1)(米
答:梯形的周长是100米;
(2)
(米
答:长方形的周长是60米;
(3)
(米
答:图形的周长是120米.
3.解:
(平方厘米)
答:图形的面积是965.625平方厘米.
4.解:
(平方分米),
答:阴影部分的面积是1500平方分米.
四、操作题
1.解:
2.解:过图中的点,画出直线的垂线(直线和直线的平行线(直线
3.解:因为平方厘米,
所以平行四边形的底和高为4厘米和3厘米,
三角形的底和高为8厘米和3厘米,
梯形的上底、下底和高为3厘米、5厘米和3厘米,
于是可以画出这几个图形:
五、解决问题
1.解:根据题干分析可得:.
答:.
2.解:小:,
,
(平方米),
大:,
,
(平方米).
因为大游泳池平均每人占6平方米,小游泳池平均每人占5平方米,所以管理员应将小聪安排在大游泳池.
3.解:它们的面积之比是:
(平方分米)
(平方分米)
(平方分米)
(平方分米)
答:甲、乙、丙三个平行四边形的面积各是60平方分米、50平方分米、30平方分米.
4.解:边上的高与边上的高的比是:;
平行四边形的底为:
(厘米);
平行四边形的面积为:
(平方厘米);
答:平行四边形的面积是420平方厘米.
5.解:
(厘米)
(平方厘米)
答:原来这个梯形的面积是192平方厘米.
6.解:(平方厘米),
(平方厘米),
(厘米),
(厘米),
,
,
(平方厘米),
,
,
(平方厘米).
答:三角形的面积是平方厘米.
一、选一选(共8小题,每小题2分,共16分)
1.下列图形中,最具有稳定性、不易变形的特性的是
A.三角形
B.平行四边形
C.正方形
D.长方形
2.用一副三角板,不能拼出 的角.
A.15度
B.20度
C.135度
D.150度
3.按记号折后能围成一个长方形的铁丝是
A.
B.
C.
4.下面能围成等腰三角形的一组小棒是
A.,,
B.,,
C.,,
5.如图,如果,那么
A.
B.
C.
6.把一个等边三角形沿其中一条高剪开,分成两个直角三角形,其中一个直角三角形的两个锐角分别是
A.和
B.和
C.和
7.一个平行四边形和一个三角形的面积相等,已知平行四边形的底是24厘米,高14厘米,三角形的底是42厘米,三角形的高是
A.336厘米
B.32厘米
C.4厘米
D.16厘米
8.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长
A.24厘米
B.12厘米
C.18厘米
D.36厘米
二、填空题(共11小题,每小题2分,共22分)
1.3时整,时针与分针所组成的角是
角,4时整,时针与分针所组成的角是
角.
2.图有
条线段,
条直线,
条射线.
3.在一个三角形中,一个角是,另一个角是,第三个角是
度,这个三角形是
三角形.
4.如果两条直线相交的夹角是,那么这两条直线相互 ,其中一条是另一条的 ,它们的交点叫做 .
5.等腰三角形中不相等的两角之比是,则它的顶角是
度或
度.
6.一个等腰三角形,两条边比是,其中最短边长度是,则这个三角形的周长是 厘米.
7.以点为顶点画一个15度的角,再以点为顶点画一个125度的角.组成三角形的另一个角是
度.
8.一块长方形的纸板,长32厘米,宽24厘米,从这块纸板上剪下一个尽可能大的正方形纸板.这块正方形纸板的面积是原来长方形纸板的 .
9.一个平行四边形的面积是72平方厘米,与它等底等高的三角形的底是18厘米.则三角形的高是 厘米.
10.一块梯形菜地,上底是45米,下底是63米,高是25米,如果每100平方米施化肥0.85千克,这块地共施化肥 千克.(得数保留两位小数)
11.平行四边形的一边长为,相邻的另一边比它的多,则这个平行四边形的周长为 .
三.计算题(共4小题,6+9+4+4=23分)
1.求图中指定角的度数.(共2小题,每小题3分,共6分)
(1)求和的度数.
(2)求的度数.
2.计算下面各图形的周长.(共3小题,每小题3分,共9分)
3.计算下面图形的面积.(单位:
4.求图中阴影部分的面积(4分).
四、操作题(共3小题,2+2+6=10分)
1.用量角器画出的角、用三角尺画出的角.
2.过图中的点,画出直线的垂线和直线的平行线.
3.在下面的方格里分别画出一个平行边形、三角形和梯形,使它们的面积都是12平方厘米.(每个小方格的面积是1平方厘米)
五、解决问题(共6小题,第27题4分,其余每题5分,共29分)
1.如图一张长方形纸,把它的一角折叠过来,已知你能求出等于多少度吗?
2.某游泳馆有大小两个游泳池,小聪来到游泳馆游泳,这时游泳池中的游泳人数情况如图.根据当时的情况,管理员应将小聪安排在哪个游泳池中?说说你的理由.
3.甲、乙、丙三个平行四边形的底之比是,高之比是,已知三个平行四边形的面积是140平方分米,那么,甲、乙、丙三个平行四边形的面积各是多少?
4.平行四边形的周长是102厘米,以为底时,高为14厘米;以为底时,高为20厘米,求平行四边形的面积.
5.有一个直角梯形,上底是下底的,如果下底减少8厘米,正好变成一个正方形,原来这个梯形的面积是多少?
6.已知,,三角形和三角形的面积,各占长方形的,求三角形的面积.
答案
一、选择题
1..2..3..4..5..6..7..8..
二、填空题
1.直,钝.
2.3,1,6.
3.:75,锐角.
4.垂直;垂线;垂足.
5.30、100.
6.50.
7.40.
8..
9.4.
10.11.48.
11.32.
三、计算题
1.解:(1)因为
所以
因为
所以.
(2)因为
所以
2.解:(1)(米
答:梯形的周长是100米;
(2)
(米
答:长方形的周长是60米;
(3)
(米
答:图形的周长是120米.
3.解:
(平方厘米)
答:图形的面积是965.625平方厘米.
4.解:
(平方分米),
答:阴影部分的面积是1500平方分米.
四、操作题
1.解:
2.解:过图中的点,画出直线的垂线(直线和直线的平行线(直线
3.解:因为平方厘米,
所以平行四边形的底和高为4厘米和3厘米,
三角形的底和高为8厘米和3厘米,
梯形的上底、下底和高为3厘米、5厘米和3厘米,
于是可以画出这几个图形:
五、解决问题
1.解:根据题干分析可得:.
答:.
2.解:小:,
,
(平方米),
大:,
,
(平方米).
因为大游泳池平均每人占6平方米,小游泳池平均每人占5平方米,所以管理员应将小聪安排在大游泳池.
3.解:它们的面积之比是:
(平方分米)
(平方分米)
(平方分米)
(平方分米)
答:甲、乙、丙三个平行四边形的面积各是60平方分米、50平方分米、30平方分米.
4.解:边上的高与边上的高的比是:;
平行四边形的底为:
(厘米);
平行四边形的面积为:
(平方厘米);
答:平行四边形的面积是420平方厘米.
5.解:
(厘米)
(平方厘米)
答:原来这个梯形的面积是192平方厘米.
6.解:(平方厘米),
(平方厘米),
(厘米),
(厘米),
,
,
(平方厘米),
,
,
(平方厘米).
答:三角形的面积是平方厘米.
