安徽省潜山野寨中学2012届下学期高三第二次周考文科数学
文档属性
| 名称 | 安徽省潜山野寨中学2012届下学期高三第二次周考文科数学 |
|
|
| 格式 | zip | ||
| 文件大小 | 184.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-13 00:00:00 | ||
图片预览




文档简介
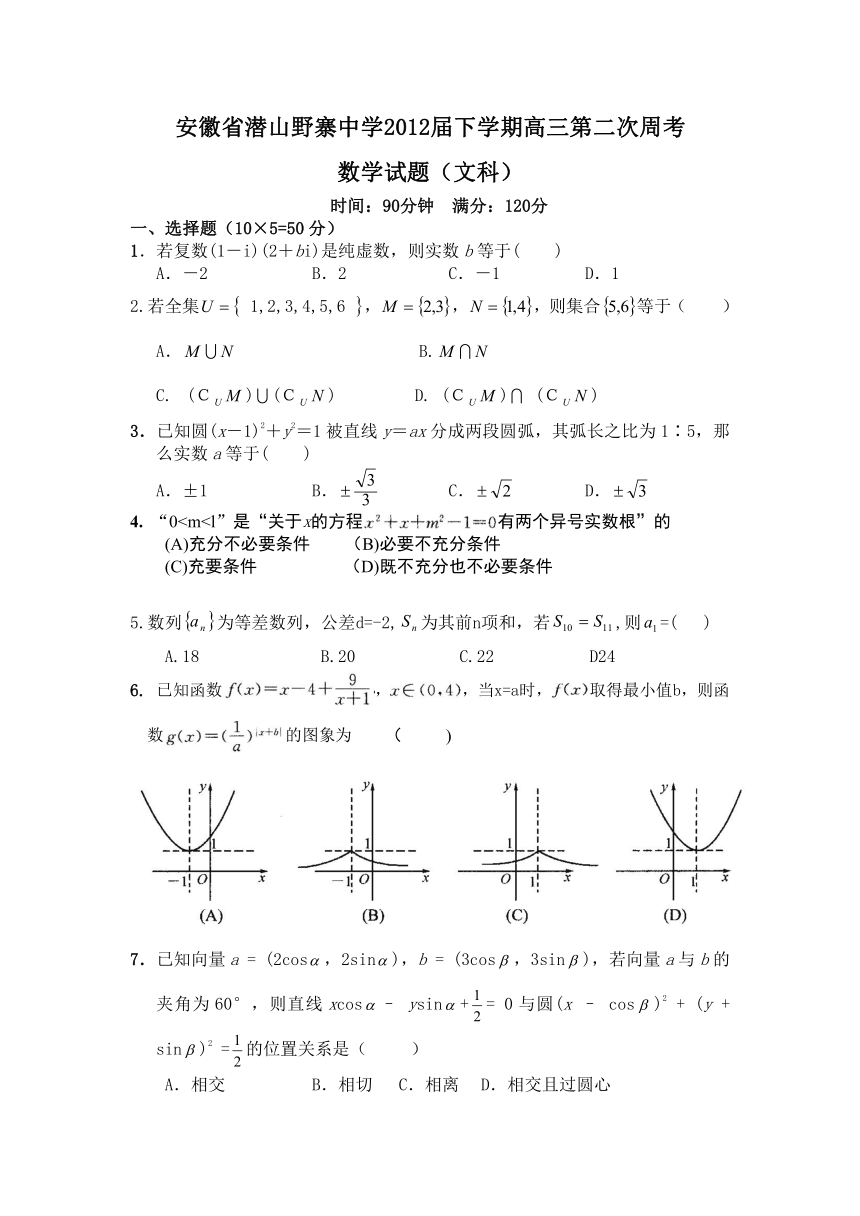
安徽省潜山野寨中学2012届下学期高三第二次周考
数学试题(文科)
时间:90分钟 满分:120分
一、选择题(10×5=50分)
1.若复数(1-i)(2+bi)是纯虚数,则实数b等于( )
A.-2 B.2 C.-1 D.1
2.若全集1,2,3,4,5,6,,,则集合等于( )
A. B.
C.(C)(C) D. (C) (C)
3.已知圆(x-1)2+y2=1被直线y=ax分成两段圆弧,其弧长之比为1∶5,那么实数a等于( )
A.±1 B. C. D.
4. “0(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
5.数列为等差数列,公差d=-2,为其前n项和,若,则=( )
A.18 B.20 C.22 D24
6. 已知函数,,当x=a时,取得最小值b,则函数的图象为 ( )
7.已知向量a = (2cos,2sin),b = (3cos,3sin),若向量a与b的夹角为60°,则直线xcos– ysin+= 0与圆(x – cos)2 + (y + sin)2 =的位置关系是( )
A.相交 B.相切 C.相离 D.相交且过圆心
8. 已知椭圆与双曲线有公共的焦点, 的一条渐近线与以的长轴为直径的圆相交于两点,若恰好将线段三等分,则
(A) (B) (C) (D)
9.已知函数f(x)=ax2+bx-1(a>0,b∈R)恰有一个零点x0∈(1,2),那么a-b的取值范围是( )
A.(-∞,-1) B.(-1,1)
C.(-1,+∞) D.(1,+∞)
10.设是定义在R上的可导函数,且满足,对任意的正数,下面不等式恒成立的是( )
A. B. C. D.;
二.填空题(5X5=25分)
11.与双曲线有相同的焦点,且过点的双曲线的标准方 程是
12. 数列中,,则数列的
前项的和为
13. 当如图所示的程序框图所输出结果为6时,在处理框中①处的数
值应该是
14.设,,,,为坐标
原点,若、、三点共线,则的最大值是 .
15.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f(x)的图象恰好通过k(k∈N*)个格点,则称函数f(x)为k阶格点函数。给出下列函数:
①f(x)=sinx; ②f(x)=π(x-1)2+3;
③ ④,
其中是一阶格点函数的有 .
三、解答题:(12+12+12+13+13+13=75分)
16. .
已知函数.
(Ⅰ) 求函数的最小值和最小正周期;
(Ⅱ)已知内角的对边分别为,且,若向量与共线,求的值.
17.某人准备购置一块占地平方米的矩形地块,中间建三个矩形温室大棚, 大棚周围均是宽为米的小路(阴影部分所示),大棚所占地面积为平方米,其中.
(1)试用表示;
(2)若要使最大,则的值各为多少?
18.甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女。
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率。
19.已知: , ,
1)求,值
2)求通项公式
附加题:(不计入总分)
20.设椭圆的右焦点为,直线与轴交于点,若(其中为坐标原点).
(1)求椭圆的方程;
(2)设是椭圆上的任意一点,为圆的任意一条直径(、为直径的两个端点),求的最大值.
21.设a>0,函数
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)求f(x)在区间[a,2a]上的最小值.
野寨中学2012届高三第二次周考数学试题(文科)答案
一、选择题(10×5=50分)
1—5:ADDAB 6—10:BCCCB
二.填空题(5X5=25分)
11. 12. 13. 10 14. 15 ①②④
三、解答题:(12+12+12+13+13+13=75分)
16.
17. 解:由题可得:,
则
.
(2)方法一:
当且仅当,即时取等号,取得最大值.此时.
所以当时,取得最大值
方法二:设 ,
,令得,
当时,,当时,.
所以当时,取得最大值.
解:(1)甲校两男教师分别用A,B表示,女教师用C表示;乙校男教师用D表示,两女教师分别用E,F表示。
从甲校和乙校报名的教师中各任选1名的所有可能的结果为:(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F)共9种
从中选出两名教师性别相同的结果有:(A,D),(B,D),(C,E),(C,F)共4种。
选出的两名教师性别相同的概率为P=
(2)从甲校和乙校报名的教师中任选2名的所有可能的结果为:略,共15种,从中选出两名教师来自同一学校的结果有:(A,B),(A,C),(B,C),(D,E),(D,F),(E,F)共6种,选出的两名教师来自同一学校的概率为P=。
19解:(1)由题设知,,,
由,得
解得.
所以椭圆的方程为.
(2)设圆的圆心为,
则
从而求的最大值转化为求的最大值.
因为是椭圆上的任意一点,设
所以,即.
因为点,所以.
因为,所以当时,取得最大值12.
所以的最大值为11.
20.解:(Ⅰ)函数f(x)的定义域为(0,+∞).
对求导数,得
解不等式得0<x<e;
解不等式得x>e
故f(x)在(0,e)上单调递增,在(e,+∞)上单调递减.
(Ⅱ)时,即时,[f(x)]min=f(a)=lna;
②当a>e时,
③当a≤e≤2a时,即时,需要比较f(a)和f(2a)的大小,
因为
所以,(1)当时,[f(x)]min=f(a)=lna;
(2)当2<a≤e时,
综上,当a≤2时,[f(x)]min=f(a)=lna;当a>2时,
21. 解:1),
2)
迭加得
(n为奇数)
同理
n为偶数
故所求
数学试题(文科)
时间:90分钟 满分:120分
一、选择题(10×5=50分)
1.若复数(1-i)(2+bi)是纯虚数,则实数b等于( )
A.-2 B.2 C.-1 D.1
2.若全集1,2,3,4,5,6,,,则集合等于( )
A. B.
C.(C)(C) D. (C) (C)
3.已知圆(x-1)2+y2=1被直线y=ax分成两段圆弧,其弧长之比为1∶5,那么实数a等于( )
A.±1 B. C. D.
4. “0
(C)充要条件 (D)既不充分也不必要条件
5.数列为等差数列,公差d=-2,为其前n项和,若,则=( )
A.18 B.20 C.22 D24
6. 已知函数,,当x=a时,取得最小值b,则函数的图象为 ( )
7.已知向量a = (2cos,2sin),b = (3cos,3sin),若向量a与b的夹角为60°,则直线xcos– ysin+= 0与圆(x – cos)2 + (y + sin)2 =的位置关系是( )
A.相交 B.相切 C.相离 D.相交且过圆心
8. 已知椭圆与双曲线有公共的焦点, 的一条渐近线与以的长轴为直径的圆相交于两点,若恰好将线段三等分,则
(A) (B) (C) (D)
9.已知函数f(x)=ax2+bx-1(a>0,b∈R)恰有一个零点x0∈(1,2),那么a-b的取值范围是( )
A.(-∞,-1) B.(-1,1)
C.(-1,+∞) D.(1,+∞)
10.设是定义在R上的可导函数,且满足,对任意的正数,下面不等式恒成立的是( )
A. B. C. D.;
二.填空题(5X5=25分)
11.与双曲线有相同的焦点,且过点的双曲线的标准方 程是
12. 数列中,,则数列的
前项的和为
13. 当如图所示的程序框图所输出结果为6时,在处理框中①处的数
值应该是
14.设,,,,为坐标
原点,若、、三点共线,则的最大值是 .
15.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f(x)的图象恰好通过k(k∈N*)个格点,则称函数f(x)为k阶格点函数。给出下列函数:
①f(x)=sinx; ②f(x)=π(x-1)2+3;
③ ④,
其中是一阶格点函数的有 .
三、解答题:(12+12+12+13+13+13=75分)
16. .
已知函数.
(Ⅰ) 求函数的最小值和最小正周期;
(Ⅱ)已知内角的对边分别为,且,若向量与共线,求的值.
17.某人准备购置一块占地平方米的矩形地块,中间建三个矩形温室大棚, 大棚周围均是宽为米的小路(阴影部分所示),大棚所占地面积为平方米,其中.
(1)试用表示;
(2)若要使最大,则的值各为多少?
18.甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女。
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率。
19.已知: , ,
1)求,值
2)求通项公式
附加题:(不计入总分)
20.设椭圆的右焦点为,直线与轴交于点,若(其中为坐标原点).
(1)求椭圆的方程;
(2)设是椭圆上的任意一点,为圆的任意一条直径(、为直径的两个端点),求的最大值.
21.设a>0,函数
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)求f(x)在区间[a,2a]上的最小值.
野寨中学2012届高三第二次周考数学试题(文科)答案
一、选择题(10×5=50分)
1—5:ADDAB 6—10:BCCCB
二.填空题(5X5=25分)
11. 12. 13. 10 14. 15 ①②④
三、解答题:(12+12+12+13+13+13=75分)
16.
17. 解:由题可得:,
则
.
(2)方法一:
当且仅当,即时取等号,取得最大值.此时.
所以当时,取得最大值
方法二:设 ,
,令得,
当时,,当时,.
所以当时,取得最大值.
解:(1)甲校两男教师分别用A,B表示,女教师用C表示;乙校男教师用D表示,两女教师分别用E,F表示。
从甲校和乙校报名的教师中各任选1名的所有可能的结果为:(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F)共9种
从中选出两名教师性别相同的结果有:(A,D),(B,D),(C,E),(C,F)共4种。
选出的两名教师性别相同的概率为P=
(2)从甲校和乙校报名的教师中任选2名的所有可能的结果为:略,共15种,从中选出两名教师来自同一学校的结果有:(A,B),(A,C),(B,C),(D,E),(D,F),(E,F)共6种,选出的两名教师来自同一学校的概率为P=。
19解:(1)由题设知,,,
由,得
解得.
所以椭圆的方程为.
(2)设圆的圆心为,
则
从而求的最大值转化为求的最大值.
因为是椭圆上的任意一点,设
所以,即.
因为点,所以.
因为,所以当时,取得最大值12.
所以的最大值为11.
20.解:(Ⅰ)函数f(x)的定义域为(0,+∞).
对求导数,得
解不等式得0<x<e;
解不等式得x>e
故f(x)在(0,e)上单调递增,在(e,+∞)上单调递减.
(Ⅱ)时,即时,[f(x)]min=f(a)=lna;
②当a>e时,
③当a≤e≤2a时,即时,需要比较f(a)和f(2a)的大小,
因为
所以,(1)当时,[f(x)]min=f(a)=lna;
(2)当2<a≤e时,
综上,当a≤2时,[f(x)]min=f(a)=lna;当a>2时,
21. 解:1),
2)
迭加得
(n为奇数)
同理
n为偶数
故所求
同课章节目录
