高中物理必修2知识梳理考点复习(共136张PPT)
文档属性
| 名称 | 高中物理必修2知识梳理考点复习(共136张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-07 17:49:25 | ||
图片预览








文档简介
(共136张PPT)
高中物理必修2
知识梳理
考点复习
说一说
砂轮打磨下来的炽热的微粒它们沿着什么方向运动
一、曲线运动的速度方向
1、质点在某一点的速度,沿曲线在这一点的切线方向。
2、曲线运动中速度的方向时刻在变,所以曲线运动是变速运动。
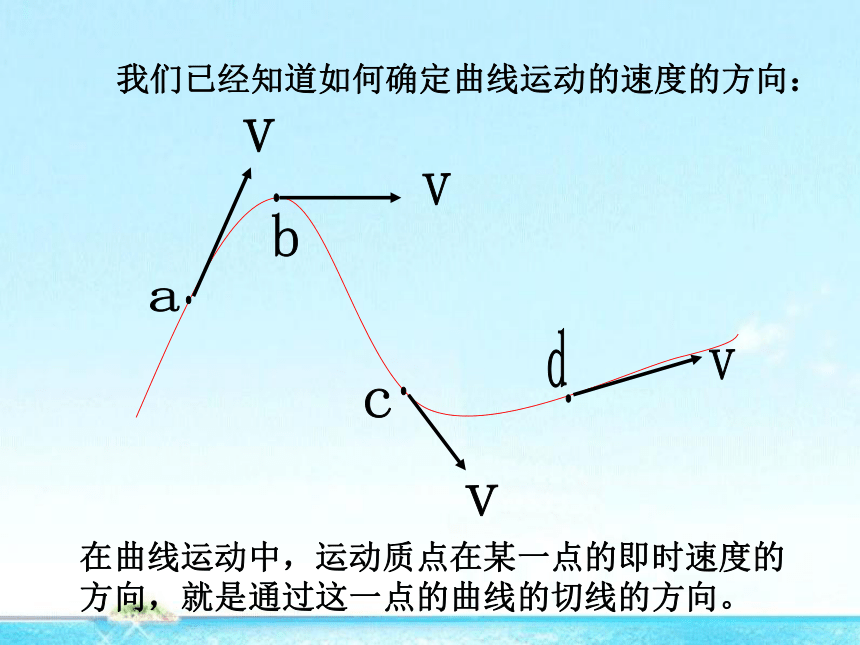
我们已经知道如何确定曲线运动的速度的方向:
在曲线运动中,运动质点在某一点的即时速度的方向,就是通过这一点的曲线的切线的方向。
课堂训练
1.关于曲线运动,下列说法正确的是 ( )
A.曲线运动一定是变速运动
B.曲线运动速度的方向不断地变化。但速度
的大小可以不变
C.曲线运动的速度方向可能不变
D.曲线运动的速度大小和方向一定同时改变
AB
实验总结
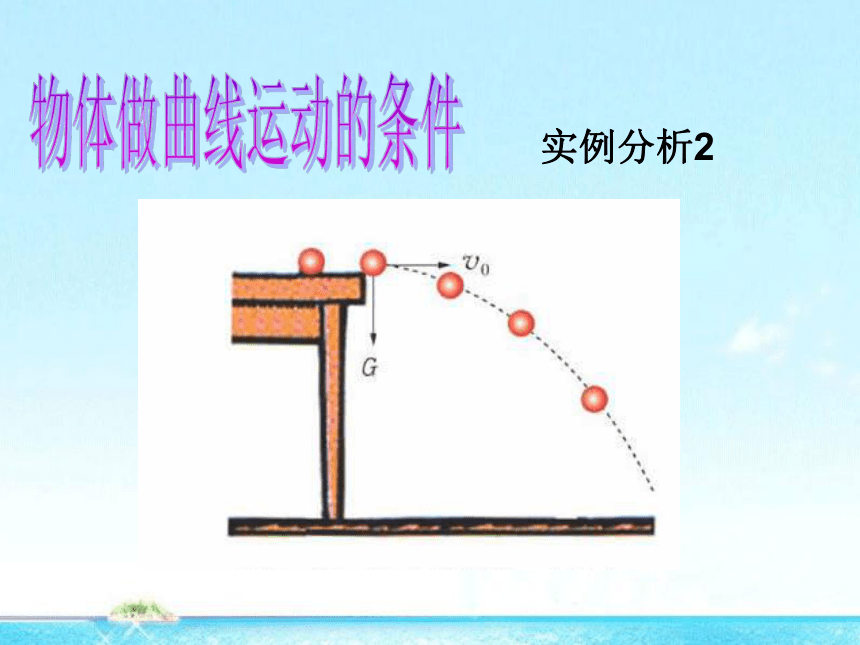
1、当物体所受的合力方向跟它的速度方向不在同一直线上时.物体将做曲线运动。
实例分析1
实例分析2
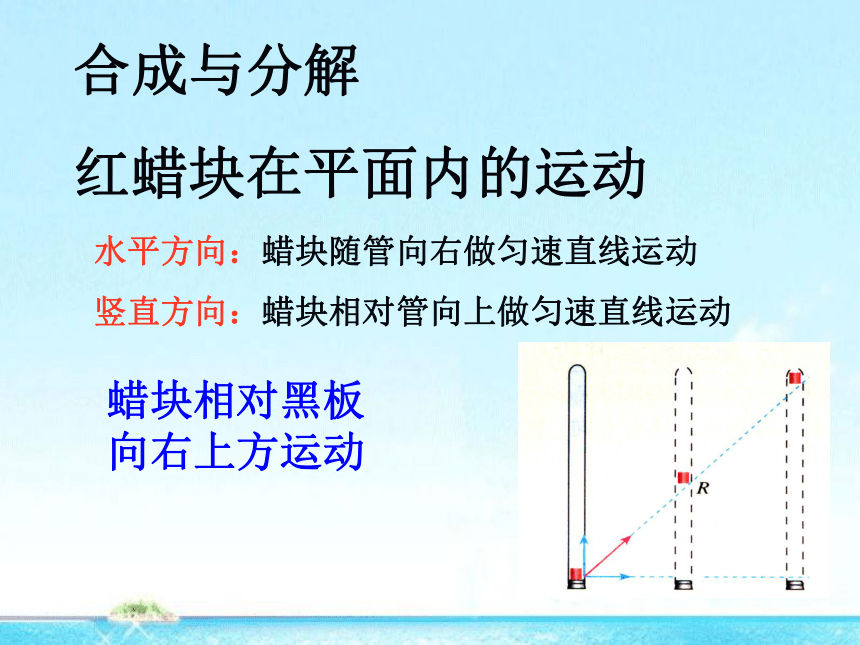
水平方向:蜡块随管向右做匀速直线运动
竖直方向:蜡块相对管向上做匀速直线运动
蜡块相对黑板 向右上方运动
合成与分解
红蜡块在平面内的运动
例:河宽d=100m,水流速度v1=3m/s,船在静水中的速度是v2=4m/s.求
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移多大?
分析1:时间最短
d
结论:当船头垂直河岸时,所用时间最短
例:河宽d=100m,水流速度v1=3m/s,船在静水中的速度是v2=4m/s.求
(2)欲使船渡河距离最短,船应怎样渡河?渡河时间多长?
分析2:航程最短
θ
d
结论:当合运动垂直河岸时,航程最短
1.关于运动的合成,下列说法中正确的是 ( )
A.合运动的速度一定比每一个分运动的速度大
B.两个速度不等的匀速直线运动的合运动,一定是匀速直线运动
C.两个分运动是直线运动的合运动,一定是直线运动
D.两个分运动的时间,一定与它们的合运动的时间相等
BD
1.基本规律:
水平方向:
竖直方向:
位移:
水平方向:
竖直方向:
合位移
大小:
方向:
速度:
合速度
大小:
方向:
2.位移变化有什么规律?相等时间内竖直位移变化呢?
1.速度变化有什么规律?
3.飞行时间和水平射程分别有什么因素决定?
4.任一时刻的末速度与初速度方向的夹角(速度偏向角)和位移与初速度方向的夹角(位移偏向角)有什么关系?
平抛运动
G
v0
v1
v2
v3
Δv
v0
Δv
Δv
v1
v2
v3
方向竖直向下
课堂练习2:
如图所示,为一物体平抛运动的x-y图象,物体从O点抛出,x、y分别为其水平和竖直位移,在物体运动过程中的任一点P(x,y),其速度的反向延长线交于x轴的A点(A点未画出),则OA的长度为( )
A. x B. 0.5x C. 0.3x D. 不能确定
B
x
y
v0
P(x,y)
O
x
y
x
y
课堂练习:将一物体以初速度V0水平抛出,不计空气阻力,求经t时间物体速度和位移?
v0
v
s
vx
vy
θ
α
速度大小:
速度方向:
位移大小:
位移方向:
θ
思考:任一时刻末速度与初速度方向的夹角和位移与初速度方向的夹角有什么关系?
G
N
F
.如何描述匀速圆周运动的快慢?
1.线速度——质点通过的圆弧长s跟所用时间t的比值。
3.周期——物体作匀速圆周运动一周所用的时间。
5.转速——单位时间内转过的圈数。
2.角速度——质点所在的半径转过的角度 跟所用时间t的比值。
即:
单位:米/秒,m/s
即:
单位:弧度/秒,rad/s
即:
单位:秒,s
即:
单位:转/秒,r/s
4.频率——1s时间内完成圆周运动的次数。
即:
单位:赫兹,Hz
v=rω
三. 实践研究:机械传动
1.链条传动 或皮带传动 2.齿轮传动
【结论】1.两种传动轮缘上的线速度大小相等。
A
B
2.共轴转动角速度相等。
二、向心加速度
r
1、做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.
a= △ v/△t
V = △ L /△t
1、下列关于向心加速度的说法中,正确的是 ( )
A.向心加速度的方向始终与速度的方向垂直
B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化
A
2、一个拖拉机后轮直径是前轮直径的2倍,当前进且不打滑时,前轮边缘上某点A的线速度与后轮边缘上某点B的线速度之比VA:VB=________,
角速度之比ωA:ωB=_________,
向心加速度之比aA:aB=_________。
1:1
2:1
2:1
分析
O
F引
F合=F引
=F向
在匀速圆周运动中,合力提供向心力
向心力
O
G
N
T
竖直方向上N=G,故T即为合力
F合=T
=F向
在匀速圆周运动中,合力提供向心力
分析
轻绳栓一小球,在光滑水平面做匀速圆周运动
小球受到哪些力的作用?
向心力由什么力提供?
r
θ
O
G
F合
T
结论:
向心力由重力G和弹力T的合力提供
思考:
小球受到哪些力的作用?
向心力由什么力提供?
结论:
向心力由重力G和弹力T的合力提供
G
f
N
滚筒洗衣机中物体跟着滚筒匀速转动时;
向心力由什么力提供?
分析
在匀速圆周运动中,合力提供向心力
小结
大小
作用效果:只改变速度的方向
方向:始终指向圆心(与v 垂直); 是变力
来源:合力提供向心力(匀速圆周运动中)
F向=m
v2
r
F向=mω2r
F向 =m r
4π2
T 2
飞机在水平面内盘旋
几种常见的圆周运动
O'
θ
ω
ω
m
O
θ
l
m
F合=Fn=mω2l sinθ
F合=Fn=mω2r
O
r
T
mg
F合
mg
F合
F升
θ
F合=mg tanθ
几种常见的圆周运动
θ
O'
O
R
ω
θ
ω
θ
m
m
F合=F向=mω2r
O
r
F合=F向=mω2 R sinθ
mg
N
F合
mg
N
F合
F合=mg tanθ
O
几种常见的圆周运动
ω
mg
N
物体相对转盘静止,随盘做匀速圆周运动
r
f静
竖直方向:N=mg
水平方向:F合=f静=mω2r
f静
v
A
B
F
a
回顾:A、B一起向左加速,分析A的受力情况。
f静
v
谁提供向心力?
静摩擦力指向圆心
向心力的分析思路
3、按序分析受力
指向圆心的合力即向心力
2、确定圆心、半径
确定圆周运动所在的平面、轨迹、圆心、半径
1、确定研究对象
小结
O
O
思考
Fn
Ft
F合
v
Fn
Ft
v
F合
速度增大的圆周运动
变速圆周运动
速度减小的圆周运动
匀速圆周运动所受的合力提供向心力,方向始终指向圆心;如果一个沿圆周运动的物体所受的合力不指向圆心,还能做匀速圆周运动吗?
当沿圆周运动的物体所受的合力不指向圆心时,物体做变速圆周运动。
切向力Ft :垂直半径方向的合力
向心力F向 :沿着半径(或指向圆心)的合力
产生切向加速度,改变速度的大小
产生向心加速度,改变速度的方向
匀速圆周运动
G
N
F
变速圆周运动
合力全部 提供向心力
合力部分 提供向心力
O
Fn
Ft
F合
v
例与练
1.关于圆周运动的合力,下列说法中正确的是 ( )
A.圆周运动的合力方向一定指向圆心
B.匀速圆周运动的合力方向一定指向圆心
C.匀速圆周运动的合力一定不变
D.匀速圆周运动的合力大小一定不变
匀速圆周运动的物体速度大小不变,速度方向不断变化。匀速圆周运动向心力只改变物体速度方向,不改变物体速度大小。
BD
例与练
2. 质量为m的球用长为L的细绳悬于天花板的O点,并使之在水平面内做匀速圆周运动,细线与竖直线成θ角,则以下正确的是 ( )
A.摆球受重力、拉力和向心力的作用
B.摆球只受重力、拉力的作用
C.摆球做匀速圆周运动的向心力为mg tanθ
D.摆球做匀速圆周运动的向心力为mg sinθ
BC
铁路的弯道
生活中的圆周运动
◆圆周运动(Circular motion)
(2) 外轨高内轨低时转弯
G
Fn
N
h
L
θ
θ
r
背景问题1、火车转弯:
2.求汽车过凹形路段最低点时对路面的压力?
N
G
【解】G和N的合力提供汽车做圆周运动的向心力,由牛顿第二定律得:
可见汽车的速度V越大,对桥的压力越大。
由于加速度a的方向竖直向上,属超重现象。
m
生活中的圆周运动
◆圆周运动(Circular motion)
FN=G
汽车过桥问题小结
eg1.一辆卡车在丘陵地匀速行驶,地形如图所示,由于轮胎太旧,途中爆胎,爆胎可能性最大的地段应是( )
A. a处 B. b处 C. c处 D. d处
生活中的圆周运动
◆圆周运动(Circular motion)
a
b
c
d
D
可能飞离路面的地段应是?
当堂练习
对宇航员,重力提供向心力:mg= mv2/r
由此可以得出
宇航员处于完全失重状态
此时人对座椅的压力为零
四离心运动
1.离心运动:做圆周运动的物体,在提供的向心力突然消失,或者不足以提供圆周运动所需的向心力的情况下,就做逐渐远离圆心的运动。
2.物体作离心运动的条件:
F合 < F需向
思考问题?
F合= F需向 做什么运动?
F合 = 0 做什么运动?
F合 <F需向 做什么运动?
F合 >F需向 做什么运动?
圆周
近心
切线
离心
离心抛掷
离心脱水
离心分离
离心甩干
●离心运动的应用
用离心机把体温计的水银柱甩回玻璃泡内
制作棉花糖的原理: 内筒与洗衣机的脱水筒相似,里面加入白砂糖,加热使糖熔化成糖汁。内筒高速旋转,黏稠的糖汁就做离心运动,从内筒壁的小孔飞散出去,成为丝状到达温度较低的外筒,并迅速冷却凝固,变得纤细雪白,像一团团棉花。
分析做圆周运动的物体受力情况
O
mg
FN
Ff
O
mg
FN
提供向心力
受力分析
Ff
FN+mg
课堂练习
航天飞机中的物体处于失重状态,是指这个物体:
(A)不受地球的吸引力;
(B)地球吸引力和向心力平衡;
(C)受的向心力和离心力平衡;
(D)对支持它的物体的压力为零。
D
拓展与思考:
汽车能通过圆形轨道的最高点吗?
R
联想:过山车上的人为什么不会掉下来
G
FN
一、竖直面内的圆周运动
1、“轻绳”模型(均是没有支撑的小球)
2、“轻杆”模型(均是有物体支撑的小球)
圆周运动中的临界问题
1、“轻绳”模型(均是没有支撑的小球)
过最高点的临界条件:
由
讨论分析:1、过最高点时, , 绳、轨道对小球产生弹力 ,方向指向圆心;
2、不能过最高点时 在到达最高点前小球已经脱离了圆轨道;
2、“轻杆”模型(均是有物体支撑的小球)
过最高点的临界条件:
小球能运动即可,
讨论分析:1、当v=0时,FN=mg,FN为支持力,沿半径指向圆心
2、当03、当
4、当 指向圆心并随v的增大而增大
所有行星分别在大小不同的椭圆轨道上围绕太阳运动,太阳是在这些椭圆的一个焦点上
第一定律(轨道定律)
一 、开普勒定律
说明:
1.不同的行星,轨道不同,半长轴不同。
2.对不同的行星,太阳总在他们的焦点上。
对每个行星来说,太阳和行星的连线在相等的时间内扫过相等的面积.
第二定律(面积定律)
则
第二定律的推论:
行星离太阳近时速度快,离太阳远时速度慢。
V1R1 =V2R2
所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等
3、第三定律:(周期定律)
注意:比值k是一个对所有行星都相同的常量,与行星无关,是只与太阳(中心天体)的质量有关的恒量。
C
太阳
半长轴a
半短轴b
A
B
行星
注意:
1.多数行星绕太阳运动的轨道十分接近圆,太阳处在圆心处。所以,中学阶段,我们把行星绕太阳的运动近似当作匀速圆周运动处理。
2. 中,比值k是一个对所有行星都相同的
常量,与行星无关,是只与太阳(中心天体)的质量有关的恒量。不同行星的半长轴不同,故公转周期也不同。
3.地球绕太阳转动,月球绕地球转动,他们遵循相同的运动规律,但是,比值K不同。
万有引力定律
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小F与物体的质量m1和m2的乘积成正比,与它们的距离r的二次方成反比.
2.公式:
m1,m2 ---两物体的质量
r ---两物体间的距离
G ---比例系数,叫引力常量,适用于任何物体,G的国际单位
N·m2/kg2
m1
m2
F
F’
r
4.公式 的适用条件:
①(理想情况)
两个质点间引力大小的计算
②(实际情况)
若两个物体间的距离远大于物体本身大小时,两个物体可看成质点
如:太阳与行星间
地球与月球间
m1
m2
F
F’
r
r 为两质点间的距离
r为两天体中心的距离
③ 质量分布均匀的两个球体,可视为质量集中于球心
r为物体到地心的距离
r为两球心间的距离
1798年,英国物理学家卡文迪许巧妙地利用扭秤装置,
第一次在实验室里对两个铅球间的引力大小F做了精确测量
和计算,比较准确地测出了引力常量G的数值
r
F
r
F
m
m
m
m
引力常量G的测量实验
G的含义—表示两质量m1 =m2=1kg的匀质小球,
相距r=1m时万有引力的大小
引力常量通常取
测定引力常量G的重要意义
1、用实验证明了万有引力的存在,使万有引力定律进入了真正实用的时代;
2、使万有引力定律公式有了真正的实用价值
可以计算天体间的引力大小,
可间接计算天体的质量、平均密度等
如:根据地球表面的重力加速度可以测定地球的质量
3.开创了微小量测量的先河,使科学放大思想得到推广;
基本思路:
将行星(或卫星)的运动看成是匀速圆周运动
分类:
1、万有引力充当向心力:F引=F向
2、在星球表面及附近:F引=G重
万有引力定律的应用
“天上”
“星球表面及附近”
万有引力 = 向心力
重力近似 =万有引力
基本方程:
辅助方程:
A
B
C
v
若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的引力,即:
式中M是地球的质量,R是地球的半径,也就是物体到地心的距离。
R
M
G
θ
m
w
r
F
向
F
引
黄金代换公式:
拓展:
例题、某宇航员驾驶航天飞机到某一星球,他使航天飞机贴近该星球附近飞行一周,测出飞行时间为4.5 103s,则该星球的平均密度是多少?
解:航天飞机绕星球飞行,万有引力提供向心力,所以
近地飞行时,r = R星
该星球的平均密度为:
联立上面三式得:
代入数值:
得:
地球
太阳
恒星
行星
认识卫星
月亮
人造卫星
卫星
赤道轨道
极地轨道
倾斜轨道
同步轨道
自转轴
卫星的轨道
卫星的轨道
卫星轨道特点:
所有卫星的轨道都必须以地心为轨道圆心或焦点。
三、地球同步卫(P54发展空间)
①定平面:轨道平面一定在赤道平面内
②定位置:在赤道正上方相对地面静止
③定周期:运动周期等于地球自转的周期
T=24h=86400s
④定轨道:轨道离地高度h=36000km
⑤定速度:线速度大小v=3.08km/s
概念:所谓地球同步卫星是指与地球自转同步,相对于地面静止的人造卫星.
对于靠近地面的卫星(近地卫星),可以认为此时的r近似等于地球半径R,把r用地球半径R代入,可以求出
这就是人造地球卫星在地面附近绕地球做匀速圆周运的最大环绕速度,叫做第一宇宙速度。
1.第一宇宙速度(环绕速度)
二、 宇宙速度
如果人造地球卫星进入地面附近的轨道速度大于7.9km/s,而小于11.2km/s,它绕地球运动的轨迹是椭圆。
当物体的速度(发射速度)大于或等于11.2km/s时,卫星就会脱离地球的引力,不再绕地球运行。我们把这个速度叫第二宇宙速度。达到第二宇宙速度的物体还受到太阳的引力。
2.第二宇宙速度(脱离速度)
卫星挣脱地球束缚的最小发射速度
达到第二宇宙速度的物体还受到太阳的引力
如果物体的(发射速度)速度等于或大于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。我们把这个速度叫第三宇宙速度。
3.第三宇宙速度(逃逸速度)
卫星挣脱太阳束缚的最小发射速度
V1=7.9km/s
1、第一宇宙速度:v=7.9km/s (地面附近、匀速圆周运动)
地球
11.2km/s>v>7.9km/s
V2=11.2km/s
2、第二宇宙速度:当物体的速度大于或等于11.2km/s时,卫星就会脱离地球的吸引,不再绕地球运行。我们把这个速度叫第二宇宙速度。达到第二宇宙速度的还受到太阳的引力。
V3=16.7km/s
3、第三宇宙速度:如果物体的速度等于或大于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。这个速度叫第三宇宙速度。
h≈0
R=6.4x106m
T=24h
h=3.6×107m
r=4.2×107m
v=3km/s
T=24h
h≈0
r=6.4×106m
v=7.9km/s
Tmin=84分钟
同步卫星
近地卫星
地球赤道上物体、近地卫星、同步卫星、月球四者比较
赤道上的物体
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
月球
500千米以下的航天器,计算时轨道半径可近似取地球半径
发射过程:
1停泊轨道 2转移轨道 3静止轨道
四、卫星的发射与回收
v1
v2
v3
1
2
3
v1
v2
v3
v4
v2>v1
v4>v3
v1>v4
v2>v1>v4>v3
卫星的变轨
A
B
已知小圆半径为R,周期为T,大圆半径为r,你能求出卫星从A运动到B的时间吗?
试比较下列各处速度和加速度的大小
a1 = a2> a3 = a4
变轨:
速度增加(F引<F向心离心运动)
半径增大(F引为阻力)速度减小 新轨道r新>r;V新<V
速度减小(F引>F向心向心运动)
半径减小(F引为动力)速度增大 新轨道r新<r;V新>V
能量分析:
飞船受轨道上稀薄空气的摩擦阻力,轨道高度会逐渐降低,由于阻力很小,轨道高度的变化很慢,卫星运行的每一圈仍可认为是匀速圆周运动。
1、发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2、沿圆轨道正常运行
只受重力
a = g
完全失重
与重力有关的现象全部消失
卫星追赶问题
1、两星相距最远的条件:
2、两星相距最近的条件:
1、宇宙飞船要与轨道空间站对接,飞船为了追上轨道空间站 ( )
A.从较低轨道上加速
B.从较高轨道上加速
C.从空间站同一高度轨道上加速
D.无论从什么轨道上加速都可以
A
2、 在发射地球同步卫星的过程中,卫星首先进入椭圆轨道Ⅰ,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道Ⅱ。则 ( )
A.该卫星的发射速度必定大于11.2km/s
B.卫星在同步轨道Ⅱ上的运行速度大于7.9km/s
C.在轨道Ⅰ上,卫星在P点的速度大于在Q点的速度
D.卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ
P
Q
Ⅰ
Ⅱ
地
C D
1、定义:
W = Fxcosα
力对物体所做的功,等于力的大小、位移的大小、力与位移夹角余弦这三者的乘积
4.1、功
3、单位
国际单位:焦耳(焦)
单位符号:J
1J=1N×1m=1N·m
2、公式
W表示力对物体所做的功,F表
示物体所受到得力,x是物体所
发生的位移,α是力F和位移x
之间的夹角,求功时一定明确要
求的是哪一个力在哪一段位移上
做的功。
功的计算时,各
量要求统一采用
国际单位制
恒力
4、对公式进行讨论
①对F:F必须是恒力
②对x:位移具有相对性,所以功也具有相对性。一般以地面为参考系。
③对α:
温馨提示:请做笔记!
注意:功的公式还可理解成在位移方向的分力与位移的乘积,或力与位移在力的方向的分量的乘积。
α COSα W 物理意义
α=π/2
0≤ α<π/2
π/2<α≤π
COSα= 0
COSα>0
COSα<0
W = 0
W > 0
W<0
不做功
正功,动力
负功,阻力
W = F x cosα
x
F1
F3
F2
5、矢量性:
标量
6、物理意义:
描述物体的运动过程的物理量 ,是力在空间上的积累效果。
7、正功和负功:
正功的意义:力对物体做正功,表明此力的效果是促进物体的运动,是动力。
负功的意义:力对物体做负功,表明此力的效果是阻碍了物体运动,是阻力。
一个力对物体做负功,也可说成物体克服这个力做了功(正值)
(1) 分别求出每个力所做的功,然后求出所有功的代数和。即:
W总=W1+W2+……+Wn
(2) 先求出物体所受的合力,然后再求出合力的功,即:W总=F合xcosα
8、如何求合力做功?
功的累积性
提醒:方法(2)仅适用于几个力同时作用于物体的情况,因为只有当这几个力同时作用于物体上时,才能求出它们的合力;方法1则不管几个力同时作用,还是作用时间有先后均适用.
温馨提示:请做笔记!
4.2. 功率
1. 定义:
功W跟完成这些功所用时间t的比值叫做功率. 符号P
2.物理意义:
反映物体做功快慢的物理量.
3. 表达式:
(1).定义式:
功率是标量,只有大小,没有方向,它的正负意义与功相同;
单位:瓦特(W)
常用单位:千瓦(kW); 马力(已废除)
1W = 1J/s
1kW=1000W
比值定义
1马力=735瓦特
因为: W = Fx cosα
(2).计算式:
故: P = W/t = Fx cosα /t
即: P = F(x /t) cosα= F v cosα
P = F v cosα
式中的α是力 F与 速度v之间的夹角.
F
X
v
F
α
4、功率、力和速度之间的关系
5、平均功率和瞬时功率
1、平均功率:
( 是平均速度 )
2、瞬时功率:
( v是瞬时速度 )
(当t很短很短时, P表示瞬时功率)
(1)
(1)
(2)
(2)
平均功率表示力在某一段时间内做功的平均快慢
瞬时功率表示力在某一时刻做功的快慢
说明:物体做匀速直线运动时,作用在物体上的恒力的瞬时功率与平均功率相等.
2.机车启动的两种方式:
(1)以恒定功率启动
6、机车起动问题
1.对机车等交通工具起动类问题,应明确P=Fv中,P为发动机的实际功率,机车正常行驶中实际功率小于或等于额定功率;F为发动机(机车)的牵引力;v为机车的瞬时速度.
Δh
h2
h1
A
B
4.3 物体从A落到B的过程中,重力做功
重力对物体做的功与路径无关,仅由物体的质量和始末两个位置的高度差 决定。
重力做功的特点:
1.重力做功特点
当物体的高度发生变化时,重力要做功。
物体下降时:
物体被举高时:
重力做正功。
重力做负功。
说明:做功的过程就是通过力传递能量的过程,
功是能量转化的量度
(如果物体在力的作用下能量发生了变化,那么这个力一定对物体做了功)
可见,重力做的功等于mgh这个量的变化.在物理学中, 就用mgh这个物理量表示物体的重力势能。
1.定义:物体的重力势能等于它所受重力与所处高度的乘积。
2.单位:国际单位制中,焦耳(J)。 1J=1kg.m.s-2 .m=1N.m
3.重力势能是标量,状态量。
4.重力势能的变化(重力势能的改变量)
ΔEP=mgh末-mgh初
Ep=mgh(h为相对参考平面的高度)
2.重力势能
1、状态量,是描述物质系统状态的物理量。
例如:位置、速度、动能、角速度、压强、温度、体积、势能等等都是状态量。物质系统在外界作用下,它的状态将随时间而发生变化,描述该系统状态量也随时间而发生变化.
2、过程量是描述物质系统状态变化过程的物理量。
例如功、速度改变量等都是过程量,它们都与一定的物理过程相对应。
过程量与状态量有何区别
类比拍照瞬间!
好像录像过程!
3、重力做功与重力势能变化关系
重力做的功等于重力势能的减少量
如果重力做正功,重力势能减少,减少的重力势能等于重力对物体做的功
如果重力做负功,重力势能增加,增加的重力势能等于物体克服重力做的功
ΔEP=EP末-EP初=mgh末-mgh初
计算重力势能之前需要先选定参考平面
在参考面下方的物体的高度是负值,重力势能也是负值。
参考平面的选取是任意的,一般选地面为参考平面
在参考面上方的物体的高度是正值,重力势能也是正值;
势能是状态量、标量.+、–表示大小(正值就比负值大)
4、重力势能的相对性
高度是相对的,所以重力势能也是相对的
重力是由于地球的吸引而使物体受到的力。也就是说,倘若没有地球,就谈不上重力。所以,严格说来,重力势能是地球与物体所组成的这个“系统”所共有的,而不是地球上的物体单独具有的。
重力势能属于物体和地球组成的系统所有 .
5.重力势能的系统性
平常所说的“物体”的重力势能,只是一种习惯简化的说法。
6、计算弹簧弹力做的功
F
l
O
弹簧的F-l 图象
7、弹簧弹性势能的表达式
其中,k是弹簧的劲度系数,
是弹簧的弹性伸长量或压缩量
弹簧处于原长时弹性势能为0,即:一般选弹簧的自由长度为零势能参考面
弹力做功与弹性势能变化的关系:
弹力做多少正(负)功,弹性势能减少(增加)多少!
从
这个式子可以看出,
左边W是合外力所做的功,所以右边的 和 应当是物体在初末两个状态的某种能量,这种能量跟物体的质量和速度直接相关,它就是物体的动能,用EK表示,即
物体的动能等于物体质量与物体速度大小的二次方乘积的一半。
对动能表达式的理解:
1、国际单位:焦耳 1kg·m2/s2=1N·m=1J
3、动能具有瞬时性,是状态量,v是瞬时速度(注意:v为合
速度或实际速度,一般都以地面为参考系)。
2、动能是标量,且没有负值,动能与物体的质量和速度大小
有关,与速度方向无关。
我们得到F做功表达式
可以写成:
合外力所做的功等于物体动能的变化。
动能定理:
合外力所做的功
末动能
初动能
改写
1、动能定理的普适性:对任何过程的恒力、变力;匀变速、非匀变速;
直线运动、曲线运动;运动全程、运动过程某一阶段或瞬间过程都能运
用;(只要不涉及加速度和时间,就可考虑用动能定理解决动力学问题)
2、动能定理的研究对象一般是一个物体,也可以是几个物体组成的系统;
4、对状态与过程关系的理解:
a.功是过程量,动能是状态量。
b.动能定理表示了过程量等于状态量的改变量的关系。(涉及一个过程两个状态)
c.动能定理反应做功的过程是能量转化的过程。等式的左边为合外力所做的功(或各个分力做功的代数和),等式右边动能的变化,指末动能EK2=1/2mv22与初能EK1=1/2mv12之差;
5、当外力做正功时,W>0,故 △Ek>0,即Ek2>Ek1,动能增加;当外力做负
功时,W<0,故△Ek<0 , 即Ek23、动能定理的计算式是标量式,遵循代数运算,v为相对地面的速度;
我们对动能定理的理解
应用动能定理解题一般步骤:
(1)明确对象和过程(通常是单个物体)
(2)做两方面的分析;
①受力分析,求各力的功及其正负,写出总功。
②确定初、末状态,写出初、末态的动能。
(3)由动能定理列方程;
例题、如图所示,一半径为R的半圆形轨道BC与一水平面相连,C为轨道的最高点,一质量为m的小球以初速度v0从圆形轨道B点进入,沿着圆形轨道运动并恰好通过最高点C,然后做平抛运动.求:
(1)小球平抛后落回水平面D点的位置距B点的距离;
(2)小球由B点沿着半圆轨道到达C点的过程中,克服轨道摩擦阻力做的功.
[来源:www.]
摩擦力(滑动摩擦力和静摩擦力)可以对物体做正功,也可以做负功,也可以不做功。
摩擦力做功:
摩擦力乘以所作用的物体通过的路程.
重力势能
弹性势能
动能
势能
机械能
三、机械能守恒定律
在只有重力做功或弹力做功的物体系统内,动能和势能会发生相互转化,但机械能的总量保持不变。
1.内容:
只有重力做功或弹力做功
3.机械能守恒条件:
(1)物体只受重力(或系统内的弹力),不受其他力,
如:所有的抛体运动(不计阻力)
v
v0
G
G
v0
G
(2)还受其他力,但只有重力(或系统内的弹力)做功,其他力不做功
如:单摆、物体沿光滑斜面下滑
(3)有系统内的内力做功,但是做功代数和为零,系统机械能守恒
F1
F2
A
B
二、机械能守恒定律常用表达式:
1、E1=E2 ( E1、E2表示系统的初、末态时的机械能)
2、 Δ EK= ΔEP (系统动能的增加量等于系统势能的减少量)
3、 Δ EA= ΔEB (系统由两个物体构成时,A的机械能的增量
等于B的机械能的减少量)
因为需要计算重力势能,所以解题时须建立重力势能的零位置,一般以
题目中的最低位置为重力势能的零位置,而且在同一问题中必须选取同一零
势能参考面。
注意:
在某些机械能守恒的问题中,运用式1 (E1=E2)求解不太方便,而运用式2 (Δ EK= ΔEP ) 、 3 (Δ EA= ΔEB )较为简单。运用式2、3的一个最大优点是不必选取零势能参考面,只要弄清楚过程中物体重力势能的变化即可。
机械能守恒定律 动能定理
应用范围 只有重力或弹力做功时的单个物体或系统 任何力作用下的单个物体或系统
关注角度 守恒的条件和初、末状态机械能的形式及大小 动能的变化及改变动能的方式(合外力做功情况)
表达式 等号两边都是机械能(或机械能的变化) 等号一边是合外力做的功,另一边是动能的变化
机械能守恒定律和动能定理比较
(1)确定研究对象,画出过程示意图;
(2)分析物体的受力,明确各力做功的情况,判断是否符合机械能守恒的条件;
(3)分析物体的运动,恰当地选取参考平面,确定物体初、末状态的机械能(势能和动能);
(4)根据机械能守恒定律列方程求解。
三、机械能守恒定律应用解题的一般步骤
例题.小球沿光滑的斜轨道由静止开始滑下,并进入在竖直平面内的离心轨道运动,如图所示,为保持小球能够通过离心轨道最高点而不落下来,求:
(1)小球至少应从多高处开始滑下?(提示:使用动能定理或机械能守恒定律)
(2)通过轨道点最低点时球对轨道压力多大?已知离心圆轨道半径为R,(不计各处摩擦。)
1. WG= E重
3. W合= EK
2. W弹= E弹
力学领域中功能关系的主要形式:
4.功 能 原 理:
其他力对物体所做的功(重力、弹力以外的力)等于物体机械能的变化:
a.当W其他>0时,△E机>0,机械能增加
b.当W其他<0时,△E机<0,机械能减少
5.系统克服摩擦力所做的总功等于系统机械能的减少量,滑动摩擦力与相对距离(或路程)的乘积在数值上等于系统产生的内能,即:
6.只有重力或弹力做功的系统,系统机械能守恒,即:
【例题4】
1、功 能 原 理:
其他力对物体所做的功(重力、弹力以外的力)等于物体机械能的变化:
请问:重力、弹力对物体做功其机械能是否发生变化?
答案:
机械能守恒定律告诉我们,在只有重力或弹力做功的物体系统内,机械能守恒。
功和能
功
功:W=FScos (只适用恒力做功)
功率:
能
动能:
势能:
Ep ′=1/2 kx2
机械能:E=EP+EK=mgh+1/2 mv2
功能关系
功是能量转化的量度——W其他=△E
动能定理
机械能守恒定律
摩擦力做功
1.摩擦力做功与路径有关。
2.静摩擦力、滑动摩擦力均可以做正功,也可以做负功,还可以不做功。
3.一对静摩擦力所做总功恒为零。
4.一对滑动摩擦力所做总功恒为负。
5.静摩擦力做功过程中,只有机械能的相互转移,没有机械能转化为其它形式的能。
6.滑动摩擦力做功的过程中,可以是产生摩擦力的物体间机械能的转移,也可以是机械能转化为内能.【 】
摩擦力的做功特点
与对应形式能量转化之间的关系:
名称 计算公式 做功特点与能量转换关系
1、作用力和反作用力做功情况没有必然联系;
2、一对相互作用的力,作用力对物体做功,反作用力不一定对物体做功;
3、作用力对物体做正功,反作用力不一定做负功;
温馨提示:请做笔记!
能量形式 涵 义 实 例
机械能 机械能是与物体的运动或位置的高度、形变相关的能量,表现为动能和势能。 流动的河水、被拉开的弓、声音等
内能 内能是组成物体的分子的无规则运动所具有的动能和势能的总和 一切由分子构成的物质
电能 电能是与电有关的能量 电器设备所消耗的的能量都是电能
电磁能 电磁能是以各种各样的电磁波的形式传播的能量 可见光、紫外线、微波和红外线等
核能 核能是一种储存在原子核内部的能量,原子核发生核反应时,会释放出巨大的能量 核潜艇、核电站、核武器等
化学能 化学能是指储存在化合物的化学键里的能量 巧克力、燃料等都储存有化学能
各种各样的能量
1、能量守恒定律的内容:
2、导致能量守恒定律最后确立的两类重要事实是什么
导致能量守恒定律最后确立的两类重要事实是确立了永动机的不可能性和发现了各种自然现象之间的相互联系与转化.
⑴、内容:
能量既不会凭空产生,也不会凭空消失,它只能从一种形式转化为另一种形式,或者从一个物体转移到另一个物体,而在转化或转移过程中,其总量保持不变.
⑵、定律的表达式
E初=E末 ;△E增=△E减
人们还提出过利用轮子的惯性、细管子的毛细作用、 电磁力、流水等获得有效动力的种种永动机设计方案,但都无一例外地失败了,17~18世纪许多机械专家就已经论证了永动机是不可能的。
法国科学院在1775年就正式决定,不再研究和试验任何永动机!
历史上有很多人不相信能量守恒定律的人,挖空心思想发明一种不消耗能量,却能不断对外做功的机器——永动机
永动不可能制成的原因 :
根据能量守恒定律,任何一部机器,只能使能量从一种形式转化为另一种形式,而不能无中生有地制造能量,因此第一类永动机是不可能制成的.
燃料燃烧时一旦把自己的热量释放出去,它就不会自动聚集起来供人类重新利用。(能量转化的方向性)
电池中的化学能转化为电能,它又通过灯泡转化成内能和光能,热和光被其他物质吸收后变为周围环境的内能,我们无法把这些内能收集起来重新利用.这种现象叫做能量的耗散.
内能总是自发地从高温物体向低温物体转移,而不会自发的由低温物体向高温物体转移.
刚煮好的鸡蛋放入凉水中
(内能: 鸡蛋 凉水)
1、机械能可以全部转化为内能;
(举例:在粗糙地面上木块由运动到静止的过程)
2、而内能不可全部转化为机械能而不引起其他变化;
热机的效率不可能100%(第二类永动机不可能存在)
(热机是指各种利用内能做功的机械,如蒸汽机、汽轮机、燃气轮机、内燃机、喷气发动机等)
例如:一辆行驶的小轿车,燃料燃烧产生的内能有370/0通过发动机散热系统排出,370/0直接由排气管排出,有260/0变为发动机输出的机械能
高中物理必修2
知识梳理
考点复习
说一说
砂轮打磨下来的炽热的微粒它们沿着什么方向运动
一、曲线运动的速度方向
1、质点在某一点的速度,沿曲线在这一点的切线方向。
2、曲线运动中速度的方向时刻在变,所以曲线运动是变速运动。
我们已经知道如何确定曲线运动的速度的方向:
在曲线运动中,运动质点在某一点的即时速度的方向,就是通过这一点的曲线的切线的方向。
课堂训练
1.关于曲线运动,下列说法正确的是 ( )
A.曲线运动一定是变速运动
B.曲线运动速度的方向不断地变化。但速度
的大小可以不变
C.曲线运动的速度方向可能不变
D.曲线运动的速度大小和方向一定同时改变
AB
实验总结
1、当物体所受的合力方向跟它的速度方向不在同一直线上时.物体将做曲线运动。
实例分析1
实例分析2
水平方向:蜡块随管向右做匀速直线运动
竖直方向:蜡块相对管向上做匀速直线运动
蜡块相对黑板 向右上方运动
合成与分解
红蜡块在平面内的运动
例:河宽d=100m,水流速度v1=3m/s,船在静水中的速度是v2=4m/s.求
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移多大?
分析1:时间最短
d
结论:当船头垂直河岸时,所用时间最短
例:河宽d=100m,水流速度v1=3m/s,船在静水中的速度是v2=4m/s.求
(2)欲使船渡河距离最短,船应怎样渡河?渡河时间多长?
分析2:航程最短
θ
d
结论:当合运动垂直河岸时,航程最短
1.关于运动的合成,下列说法中正确的是 ( )
A.合运动的速度一定比每一个分运动的速度大
B.两个速度不等的匀速直线运动的合运动,一定是匀速直线运动
C.两个分运动是直线运动的合运动,一定是直线运动
D.两个分运动的时间,一定与它们的合运动的时间相等
BD
1.基本规律:
水平方向:
竖直方向:
位移:
水平方向:
竖直方向:
合位移
大小:
方向:
速度:
合速度
大小:
方向:
2.位移变化有什么规律?相等时间内竖直位移变化呢?
1.速度变化有什么规律?
3.飞行时间和水平射程分别有什么因素决定?
4.任一时刻的末速度与初速度方向的夹角(速度偏向角)和位移与初速度方向的夹角(位移偏向角)有什么关系?
平抛运动
G
v0
v1
v2
v3
Δv
v0
Δv
Δv
v1
v2
v3
方向竖直向下
课堂练习2:
如图所示,为一物体平抛运动的x-y图象,物体从O点抛出,x、y分别为其水平和竖直位移,在物体运动过程中的任一点P(x,y),其速度的反向延长线交于x轴的A点(A点未画出),则OA的长度为( )
A. x B. 0.5x C. 0.3x D. 不能确定
B
x
y
v0
P(x,y)
O
x
y
x
y
课堂练习:将一物体以初速度V0水平抛出,不计空气阻力,求经t时间物体速度和位移?
v0
v
s
vx
vy
θ
α
速度大小:
速度方向:
位移大小:
位移方向:
θ
思考:任一时刻末速度与初速度方向的夹角和位移与初速度方向的夹角有什么关系?
G
N
F
.如何描述匀速圆周运动的快慢?
1.线速度——质点通过的圆弧长s跟所用时间t的比值。
3.周期——物体作匀速圆周运动一周所用的时间。
5.转速——单位时间内转过的圈数。
2.角速度——质点所在的半径转过的角度 跟所用时间t的比值。
即:
单位:米/秒,m/s
即:
单位:弧度/秒,rad/s
即:
单位:秒,s
即:
单位:转/秒,r/s
4.频率——1s时间内完成圆周运动的次数。
即:
单位:赫兹,Hz
v=rω
三. 实践研究:机械传动
1.链条传动 或皮带传动 2.齿轮传动
【结论】1.两种传动轮缘上的线速度大小相等。
A
B
2.共轴转动角速度相等。
二、向心加速度
r
1、做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.
a= △ v/△t
V = △ L /△t
1、下列关于向心加速度的说法中,正确的是 ( )
A.向心加速度的方向始终与速度的方向垂直
B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化
A
2、一个拖拉机后轮直径是前轮直径的2倍,当前进且不打滑时,前轮边缘上某点A的线速度与后轮边缘上某点B的线速度之比VA:VB=________,
角速度之比ωA:ωB=_________,
向心加速度之比aA:aB=_________。
1:1
2:1
2:1
分析
O
F引
F合=F引
=F向
在匀速圆周运动中,合力提供向心力
向心力
O
G
N
T
竖直方向上N=G,故T即为合力
F合=T
=F向
在匀速圆周运动中,合力提供向心力
分析
轻绳栓一小球,在光滑水平面做匀速圆周运动
小球受到哪些力的作用?
向心力由什么力提供?
r
θ
O
G
F合
T
结论:
向心力由重力G和弹力T的合力提供
思考:
小球受到哪些力的作用?
向心力由什么力提供?
结论:
向心力由重力G和弹力T的合力提供
G
f
N
滚筒洗衣机中物体跟着滚筒匀速转动时;
向心力由什么力提供?
分析
在匀速圆周运动中,合力提供向心力
小结
大小
作用效果:只改变速度的方向
方向:始终指向圆心(与v 垂直); 是变力
来源:合力提供向心力(匀速圆周运动中)
F向=m
v2
r
F向=mω2r
F向 =m r
4π2
T 2
飞机在水平面内盘旋
几种常见的圆周运动
O'
θ
ω
ω
m
O
θ
l
m
F合=Fn=mω2l sinθ
F合=Fn=mω2r
O
r
T
mg
F合
mg
F合
F升
θ
F合=mg tanθ
几种常见的圆周运动
θ
O'
O
R
ω
θ
ω
θ
m
m
F合=F向=mω2r
O
r
F合=F向=mω2 R sinθ
mg
N
F合
mg
N
F合
F合=mg tanθ
O
几种常见的圆周运动
ω
mg
N
物体相对转盘静止,随盘做匀速圆周运动
r
f静
竖直方向:N=mg
水平方向:F合=f静=mω2r
f静
v
A
B
F
a
回顾:A、B一起向左加速,分析A的受力情况。
f静
v
谁提供向心力?
静摩擦力指向圆心
向心力的分析思路
3、按序分析受力
指向圆心的合力即向心力
2、确定圆心、半径
确定圆周运动所在的平面、轨迹、圆心、半径
1、确定研究对象
小结
O
O
思考
Fn
Ft
F合
v
Fn
Ft
v
F合
速度增大的圆周运动
变速圆周运动
速度减小的圆周运动
匀速圆周运动所受的合力提供向心力,方向始终指向圆心;如果一个沿圆周运动的物体所受的合力不指向圆心,还能做匀速圆周运动吗?
当沿圆周运动的物体所受的合力不指向圆心时,物体做变速圆周运动。
切向力Ft :垂直半径方向的合力
向心力F向 :沿着半径(或指向圆心)的合力
产生切向加速度,改变速度的大小
产生向心加速度,改变速度的方向
匀速圆周运动
G
N
F
变速圆周运动
合力全部 提供向心力
合力部分 提供向心力
O
Fn
Ft
F合
v
例与练
1.关于圆周运动的合力,下列说法中正确的是 ( )
A.圆周运动的合力方向一定指向圆心
B.匀速圆周运动的合力方向一定指向圆心
C.匀速圆周运动的合力一定不变
D.匀速圆周运动的合力大小一定不变
匀速圆周运动的物体速度大小不变,速度方向不断变化。匀速圆周运动向心力只改变物体速度方向,不改变物体速度大小。
BD
例与练
2. 质量为m的球用长为L的细绳悬于天花板的O点,并使之在水平面内做匀速圆周运动,细线与竖直线成θ角,则以下正确的是 ( )
A.摆球受重力、拉力和向心力的作用
B.摆球只受重力、拉力的作用
C.摆球做匀速圆周运动的向心力为mg tanθ
D.摆球做匀速圆周运动的向心力为mg sinθ
BC
铁路的弯道
生活中的圆周运动
◆圆周运动(Circular motion)
(2) 外轨高内轨低时转弯
G
Fn
N
h
L
θ
θ
r
背景问题1、火车转弯:
2.求汽车过凹形路段最低点时对路面的压力?
N
G
【解】G和N的合力提供汽车做圆周运动的向心力,由牛顿第二定律得:
可见汽车的速度V越大,对桥的压力越大。
由于加速度a的方向竖直向上,属超重现象。
m
生活中的圆周运动
◆圆周运动(Circular motion)
FN=G
汽车过桥问题小结
eg1.一辆卡车在丘陵地匀速行驶,地形如图所示,由于轮胎太旧,途中爆胎,爆胎可能性最大的地段应是( )
A. a处 B. b处 C. c处 D. d处
生活中的圆周运动
◆圆周运动(Circular motion)
a
b
c
d
D
可能飞离路面的地段应是?
当堂练习
对宇航员,重力提供向心力:mg= mv2/r
由此可以得出
宇航员处于完全失重状态
此时人对座椅的压力为零
四离心运动
1.离心运动:做圆周运动的物体,在提供的向心力突然消失,或者不足以提供圆周运动所需的向心力的情况下,就做逐渐远离圆心的运动。
2.物体作离心运动的条件:
F合 < F需向
思考问题?
F合= F需向 做什么运动?
F合 = 0 做什么运动?
F合 <F需向 做什么运动?
F合 >F需向 做什么运动?
圆周
近心
切线
离心
离心抛掷
离心脱水
离心分离
离心甩干
●离心运动的应用
用离心机把体温计的水银柱甩回玻璃泡内
制作棉花糖的原理: 内筒与洗衣机的脱水筒相似,里面加入白砂糖,加热使糖熔化成糖汁。内筒高速旋转,黏稠的糖汁就做离心运动,从内筒壁的小孔飞散出去,成为丝状到达温度较低的外筒,并迅速冷却凝固,变得纤细雪白,像一团团棉花。
分析做圆周运动的物体受力情况
O
mg
FN
Ff
O
mg
FN
提供向心力
受力分析
Ff
FN+mg
课堂练习
航天飞机中的物体处于失重状态,是指这个物体:
(A)不受地球的吸引力;
(B)地球吸引力和向心力平衡;
(C)受的向心力和离心力平衡;
(D)对支持它的物体的压力为零。
D
拓展与思考:
汽车能通过圆形轨道的最高点吗?
R
联想:过山车上的人为什么不会掉下来
G
FN
一、竖直面内的圆周运动
1、“轻绳”模型(均是没有支撑的小球)
2、“轻杆”模型(均是有物体支撑的小球)
圆周运动中的临界问题
1、“轻绳”模型(均是没有支撑的小球)
过最高点的临界条件:
由
讨论分析:1、过最高点时, , 绳、轨道对小球产生弹力 ,方向指向圆心;
2、不能过最高点时 在到达最高点前小球已经脱离了圆轨道;
2、“轻杆”模型(均是有物体支撑的小球)
过最高点的临界条件:
小球能运动即可,
讨论分析:1、当v=0时,FN=mg,FN为支持力,沿半径指向圆心
2、当0
4、当 指向圆心并随v的增大而增大
所有行星分别在大小不同的椭圆轨道上围绕太阳运动,太阳是在这些椭圆的一个焦点上
第一定律(轨道定律)
一 、开普勒定律
说明:
1.不同的行星,轨道不同,半长轴不同。
2.对不同的行星,太阳总在他们的焦点上。
对每个行星来说,太阳和行星的连线在相等的时间内扫过相等的面积.
第二定律(面积定律)
则
第二定律的推论:
行星离太阳近时速度快,离太阳远时速度慢。
V1R1 =V2R2
所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等
3、第三定律:(周期定律)
注意:比值k是一个对所有行星都相同的常量,与行星无关,是只与太阳(中心天体)的质量有关的恒量。
C
太阳
半长轴a
半短轴b
A
B
行星
注意:
1.多数行星绕太阳运动的轨道十分接近圆,太阳处在圆心处。所以,中学阶段,我们把行星绕太阳的运动近似当作匀速圆周运动处理。
2. 中,比值k是一个对所有行星都相同的
常量,与行星无关,是只与太阳(中心天体)的质量有关的恒量。不同行星的半长轴不同,故公转周期也不同。
3.地球绕太阳转动,月球绕地球转动,他们遵循相同的运动规律,但是,比值K不同。
万有引力定律
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小F与物体的质量m1和m2的乘积成正比,与它们的距离r的二次方成反比.
2.公式:
m1,m2 ---两物体的质量
r ---两物体间的距离
G ---比例系数,叫引力常量,适用于任何物体,G的国际单位
N·m2/kg2
m1
m2
F
F’
r
4.公式 的适用条件:
①(理想情况)
两个质点间引力大小的计算
②(实际情况)
若两个物体间的距离远大于物体本身大小时,两个物体可看成质点
如:太阳与行星间
地球与月球间
m1
m2
F
F’
r
r 为两质点间的距离
r为两天体中心的距离
③ 质量分布均匀的两个球体,可视为质量集中于球心
r为物体到地心的距离
r为两球心间的距离
1798年,英国物理学家卡文迪许巧妙地利用扭秤装置,
第一次在实验室里对两个铅球间的引力大小F做了精确测量
和计算,比较准确地测出了引力常量G的数值
r
F
r
F
m
m
m
m
引力常量G的测量实验
G的含义—表示两质量m1 =m2=1kg的匀质小球,
相距r=1m时万有引力的大小
引力常量通常取
测定引力常量G的重要意义
1、用实验证明了万有引力的存在,使万有引力定律进入了真正实用的时代;
2、使万有引力定律公式有了真正的实用价值
可以计算天体间的引力大小,
可间接计算天体的质量、平均密度等
如:根据地球表面的重力加速度可以测定地球的质量
3.开创了微小量测量的先河,使科学放大思想得到推广;
基本思路:
将行星(或卫星)的运动看成是匀速圆周运动
分类:
1、万有引力充当向心力:F引=F向
2、在星球表面及附近:F引=G重
万有引力定律的应用
“天上”
“星球表面及附近”
万有引力 = 向心力
重力近似 =万有引力
基本方程:
辅助方程:
A
B
C
v
若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的引力,即:
式中M是地球的质量,R是地球的半径,也就是物体到地心的距离。
R
M
G
θ
m
w
r
F
向
F
引
黄金代换公式:
拓展:
例题、某宇航员驾驶航天飞机到某一星球,他使航天飞机贴近该星球附近飞行一周,测出飞行时间为4.5 103s,则该星球的平均密度是多少?
解:航天飞机绕星球飞行,万有引力提供向心力,所以
近地飞行时,r = R星
该星球的平均密度为:
联立上面三式得:
代入数值:
得:
地球
太阳
恒星
行星
认识卫星
月亮
人造卫星
卫星
赤道轨道
极地轨道
倾斜轨道
同步轨道
自转轴
卫星的轨道
卫星的轨道
卫星轨道特点:
所有卫星的轨道都必须以地心为轨道圆心或焦点。
三、地球同步卫(P54发展空间)
①定平面:轨道平面一定在赤道平面内
②定位置:在赤道正上方相对地面静止
③定周期:运动周期等于地球自转的周期
T=24h=86400s
④定轨道:轨道离地高度h=36000km
⑤定速度:线速度大小v=3.08km/s
概念:所谓地球同步卫星是指与地球自转同步,相对于地面静止的人造卫星.
对于靠近地面的卫星(近地卫星),可以认为此时的r近似等于地球半径R,把r用地球半径R代入,可以求出
这就是人造地球卫星在地面附近绕地球做匀速圆周运的最大环绕速度,叫做第一宇宙速度。
1.第一宇宙速度(环绕速度)
二、 宇宙速度
如果人造地球卫星进入地面附近的轨道速度大于7.9km/s,而小于11.2km/s,它绕地球运动的轨迹是椭圆。
当物体的速度(发射速度)大于或等于11.2km/s时,卫星就会脱离地球的引力,不再绕地球运行。我们把这个速度叫第二宇宙速度。达到第二宇宙速度的物体还受到太阳的引力。
2.第二宇宙速度(脱离速度)
卫星挣脱地球束缚的最小发射速度
达到第二宇宙速度的物体还受到太阳的引力
如果物体的(发射速度)速度等于或大于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。我们把这个速度叫第三宇宙速度。
3.第三宇宙速度(逃逸速度)
卫星挣脱太阳束缚的最小发射速度
V1=7.9km/s
1、第一宇宙速度:v=7.9km/s (地面附近、匀速圆周运动)
地球
11.2km/s>v>7.9km/s
V2=11.2km/s
2、第二宇宙速度:当物体的速度大于或等于11.2km/s时,卫星就会脱离地球的吸引,不再绕地球运行。我们把这个速度叫第二宇宙速度。达到第二宇宙速度的还受到太阳的引力。
V3=16.7km/s
3、第三宇宙速度:如果物体的速度等于或大于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。这个速度叫第三宇宙速度。
h≈0
R=6.4x106m
T=24h
h=3.6×107m
r=4.2×107m
v=3km/s
T=24h
h≈0
r=6.4×106m
v=7.9km/s
Tmin=84分钟
同步卫星
近地卫星
地球赤道上物体、近地卫星、同步卫星、月球四者比较
赤道上的物体
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
月球
500千米以下的航天器,计算时轨道半径可近似取地球半径
发射过程:
1停泊轨道 2转移轨道 3静止轨道
四、卫星的发射与回收
v1
v2
v3
1
2
3
v1
v2
v3
v4
v2>v1
v4>v3
v1>v4
v2>v1>v4>v3
卫星的变轨
A
B
已知小圆半径为R,周期为T,大圆半径为r,你能求出卫星从A运动到B的时间吗?
试比较下列各处速度和加速度的大小
a1 = a2> a3 = a4
变轨:
速度增加(F引<F向心离心运动)
半径增大(F引为阻力)速度减小 新轨道r新>r;V新<V
速度减小(F引>F向心向心运动)
半径减小(F引为动力)速度增大 新轨道r新<r;V新>V
能量分析:
飞船受轨道上稀薄空气的摩擦阻力,轨道高度会逐渐降低,由于阻力很小,轨道高度的变化很慢,卫星运行的每一圈仍可认为是匀速圆周运动。
1、发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2、沿圆轨道正常运行
只受重力
a = g
完全失重
与重力有关的现象全部消失
卫星追赶问题
1、两星相距最远的条件:
2、两星相距最近的条件:
1、宇宙飞船要与轨道空间站对接,飞船为了追上轨道空间站 ( )
A.从较低轨道上加速
B.从较高轨道上加速
C.从空间站同一高度轨道上加速
D.无论从什么轨道上加速都可以
A
2、 在发射地球同步卫星的过程中,卫星首先进入椭圆轨道Ⅰ,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道Ⅱ。则 ( )
A.该卫星的发射速度必定大于11.2km/s
B.卫星在同步轨道Ⅱ上的运行速度大于7.9km/s
C.在轨道Ⅰ上,卫星在P点的速度大于在Q点的速度
D.卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ
P
Q
Ⅰ
Ⅱ
地
C D
1、定义:
W = Fxcosα
力对物体所做的功,等于力的大小、位移的大小、力与位移夹角余弦这三者的乘积
4.1、功
3、单位
国际单位:焦耳(焦)
单位符号:J
1J=1N×1m=1N·m
2、公式
W表示力对物体所做的功,F表
示物体所受到得力,x是物体所
发生的位移,α是力F和位移x
之间的夹角,求功时一定明确要
求的是哪一个力在哪一段位移上
做的功。
功的计算时,各
量要求统一采用
国际单位制
恒力
4、对公式进行讨论
①对F:F必须是恒力
②对x:位移具有相对性,所以功也具有相对性。一般以地面为参考系。
③对α:
温馨提示:请做笔记!
注意:功的公式还可理解成在位移方向的分力与位移的乘积,或力与位移在力的方向的分量的乘积。
α COSα W 物理意义
α=π/2
0≤ α<π/2
π/2<α≤π
COSα= 0
COSα>0
COSα<0
W = 0
W > 0
W<0
不做功
正功,动力
负功,阻力
W = F x cosα
x
F1
F3
F2
5、矢量性:
标量
6、物理意义:
描述物体的运动过程的物理量 ,是力在空间上的积累效果。
7、正功和负功:
正功的意义:力对物体做正功,表明此力的效果是促进物体的运动,是动力。
负功的意义:力对物体做负功,表明此力的效果是阻碍了物体运动,是阻力。
一个力对物体做负功,也可说成物体克服这个力做了功(正值)
(1) 分别求出每个力所做的功,然后求出所有功的代数和。即:
W总=W1+W2+……+Wn
(2) 先求出物体所受的合力,然后再求出合力的功,即:W总=F合xcosα
8、如何求合力做功?
功的累积性
提醒:方法(2)仅适用于几个力同时作用于物体的情况,因为只有当这几个力同时作用于物体上时,才能求出它们的合力;方法1则不管几个力同时作用,还是作用时间有先后均适用.
温馨提示:请做笔记!
4.2. 功率
1. 定义:
功W跟完成这些功所用时间t的比值叫做功率. 符号P
2.物理意义:
反映物体做功快慢的物理量.
3. 表达式:
(1).定义式:
功率是标量,只有大小,没有方向,它的正负意义与功相同;
单位:瓦特(W)
常用单位:千瓦(kW); 马力(已废除)
1W = 1J/s
1kW=1000W
比值定义
1马力=735瓦特
因为: W = Fx cosα
(2).计算式:
故: P = W/t = Fx cosα /t
即: P = F(x /t) cosα= F v cosα
P = F v cosα
式中的α是力 F与 速度v之间的夹角.
F
X
v
F
α
4、功率、力和速度之间的关系
5、平均功率和瞬时功率
1、平均功率:
( 是平均速度 )
2、瞬时功率:
( v是瞬时速度 )
(当t很短很短时, P表示瞬时功率)
(1)
(1)
(2)
(2)
平均功率表示力在某一段时间内做功的平均快慢
瞬时功率表示力在某一时刻做功的快慢
说明:物体做匀速直线运动时,作用在物体上的恒力的瞬时功率与平均功率相等.
2.机车启动的两种方式:
(1)以恒定功率启动
6、机车起动问题
1.对机车等交通工具起动类问题,应明确P=Fv中,P为发动机的实际功率,机车正常行驶中实际功率小于或等于额定功率;F为发动机(机车)的牵引力;v为机车的瞬时速度.
Δh
h2
h1
A
B
4.3 物体从A落到B的过程中,重力做功
重力对物体做的功与路径无关,仅由物体的质量和始末两个位置的高度差 决定。
重力做功的特点:
1.重力做功特点
当物体的高度发生变化时,重力要做功。
物体下降时:
物体被举高时:
重力做正功。
重力做负功。
说明:做功的过程就是通过力传递能量的过程,
功是能量转化的量度
(如果物体在力的作用下能量发生了变化,那么这个力一定对物体做了功)
可见,重力做的功等于mgh这个量的变化.在物理学中, 就用mgh这个物理量表示物体的重力势能。
1.定义:物体的重力势能等于它所受重力与所处高度的乘积。
2.单位:国际单位制中,焦耳(J)。 1J=1kg.m.s-2 .m=1N.m
3.重力势能是标量,状态量。
4.重力势能的变化(重力势能的改变量)
ΔEP=mgh末-mgh初
Ep=mgh(h为相对参考平面的高度)
2.重力势能
1、状态量,是描述物质系统状态的物理量。
例如:位置、速度、动能、角速度、压强、温度、体积、势能等等都是状态量。物质系统在外界作用下,它的状态将随时间而发生变化,描述该系统状态量也随时间而发生变化.
2、过程量是描述物质系统状态变化过程的物理量。
例如功、速度改变量等都是过程量,它们都与一定的物理过程相对应。
过程量与状态量有何区别
类比拍照瞬间!
好像录像过程!
3、重力做功与重力势能变化关系
重力做的功等于重力势能的减少量
如果重力做正功,重力势能减少,减少的重力势能等于重力对物体做的功
如果重力做负功,重力势能增加,增加的重力势能等于物体克服重力做的功
ΔEP=EP末-EP初=mgh末-mgh初
计算重力势能之前需要先选定参考平面
在参考面下方的物体的高度是负值,重力势能也是负值。
参考平面的选取是任意的,一般选地面为参考平面
在参考面上方的物体的高度是正值,重力势能也是正值;
势能是状态量、标量.+、–表示大小(正值就比负值大)
4、重力势能的相对性
高度是相对的,所以重力势能也是相对的
重力是由于地球的吸引而使物体受到的力。也就是说,倘若没有地球,就谈不上重力。所以,严格说来,重力势能是地球与物体所组成的这个“系统”所共有的,而不是地球上的物体单独具有的。
重力势能属于物体和地球组成的系统所有 .
5.重力势能的系统性
平常所说的“物体”的重力势能,只是一种习惯简化的说法。
6、计算弹簧弹力做的功
F
l
O
弹簧的F-l 图象
7、弹簧弹性势能的表达式
其中,k是弹簧的劲度系数,
是弹簧的弹性伸长量或压缩量
弹簧处于原长时弹性势能为0,即:一般选弹簧的自由长度为零势能参考面
弹力做功与弹性势能变化的关系:
弹力做多少正(负)功,弹性势能减少(增加)多少!
从
这个式子可以看出,
左边W是合外力所做的功,所以右边的 和 应当是物体在初末两个状态的某种能量,这种能量跟物体的质量和速度直接相关,它就是物体的动能,用EK表示,即
物体的动能等于物体质量与物体速度大小的二次方乘积的一半。
对动能表达式的理解:
1、国际单位:焦耳 1kg·m2/s2=1N·m=1J
3、动能具有瞬时性,是状态量,v是瞬时速度(注意:v为合
速度或实际速度,一般都以地面为参考系)。
2、动能是标量,且没有负值,动能与物体的质量和速度大小
有关,与速度方向无关。
我们得到F做功表达式
可以写成:
合外力所做的功等于物体动能的变化。
动能定理:
合外力所做的功
末动能
初动能
改写
1、动能定理的普适性:对任何过程的恒力、变力;匀变速、非匀变速;
直线运动、曲线运动;运动全程、运动过程某一阶段或瞬间过程都能运
用;(只要不涉及加速度和时间,就可考虑用动能定理解决动力学问题)
2、动能定理的研究对象一般是一个物体,也可以是几个物体组成的系统;
4、对状态与过程关系的理解:
a.功是过程量,动能是状态量。
b.动能定理表示了过程量等于状态量的改变量的关系。(涉及一个过程两个状态)
c.动能定理反应做功的过程是能量转化的过程。等式的左边为合外力所做的功(或各个分力做功的代数和),等式右边动能的变化,指末动能EK2=1/2mv22与初能EK1=1/2mv12之差;
5、当外力做正功时,W>0,故 △Ek>0,即Ek2>Ek1,动能增加;当外力做负
功时,W<0,故△Ek<0 , 即Ek2
我们对动能定理的理解
应用动能定理解题一般步骤:
(1)明确对象和过程(通常是单个物体)
(2)做两方面的分析;
①受力分析,求各力的功及其正负,写出总功。
②确定初、末状态,写出初、末态的动能。
(3)由动能定理列方程;
例题、如图所示,一半径为R的半圆形轨道BC与一水平面相连,C为轨道的最高点,一质量为m的小球以初速度v0从圆形轨道B点进入,沿着圆形轨道运动并恰好通过最高点C,然后做平抛运动.求:
(1)小球平抛后落回水平面D点的位置距B点的距离;
(2)小球由B点沿着半圆轨道到达C点的过程中,克服轨道摩擦阻力做的功.
[来源:www.]
摩擦力(滑动摩擦力和静摩擦力)可以对物体做正功,也可以做负功,也可以不做功。
摩擦力做功:
摩擦力乘以所作用的物体通过的路程.
重力势能
弹性势能
动能
势能
机械能
三、机械能守恒定律
在只有重力做功或弹力做功的物体系统内,动能和势能会发生相互转化,但机械能的总量保持不变。
1.内容:
只有重力做功或弹力做功
3.机械能守恒条件:
(1)物体只受重力(或系统内的弹力),不受其他力,
如:所有的抛体运动(不计阻力)
v
v0
G
G
v0
G
(2)还受其他力,但只有重力(或系统内的弹力)做功,其他力不做功
如:单摆、物体沿光滑斜面下滑
(3)有系统内的内力做功,但是做功代数和为零,系统机械能守恒
F1
F2
A
B
二、机械能守恒定律常用表达式:
1、E1=E2 ( E1、E2表示系统的初、末态时的机械能)
2、 Δ EK= ΔEP (系统动能的增加量等于系统势能的减少量)
3、 Δ EA= ΔEB (系统由两个物体构成时,A的机械能的增量
等于B的机械能的减少量)
因为需要计算重力势能,所以解题时须建立重力势能的零位置,一般以
题目中的最低位置为重力势能的零位置,而且在同一问题中必须选取同一零
势能参考面。
注意:
在某些机械能守恒的问题中,运用式1 (E1=E2)求解不太方便,而运用式2 (Δ EK= ΔEP ) 、 3 (Δ EA= ΔEB )较为简单。运用式2、3的一个最大优点是不必选取零势能参考面,只要弄清楚过程中物体重力势能的变化即可。
机械能守恒定律 动能定理
应用范围 只有重力或弹力做功时的单个物体或系统 任何力作用下的单个物体或系统
关注角度 守恒的条件和初、末状态机械能的形式及大小 动能的变化及改变动能的方式(合外力做功情况)
表达式 等号两边都是机械能(或机械能的变化) 等号一边是合外力做的功,另一边是动能的变化
机械能守恒定律和动能定理比较
(1)确定研究对象,画出过程示意图;
(2)分析物体的受力,明确各力做功的情况,判断是否符合机械能守恒的条件;
(3)分析物体的运动,恰当地选取参考平面,确定物体初、末状态的机械能(势能和动能);
(4)根据机械能守恒定律列方程求解。
三、机械能守恒定律应用解题的一般步骤
例题.小球沿光滑的斜轨道由静止开始滑下,并进入在竖直平面内的离心轨道运动,如图所示,为保持小球能够通过离心轨道最高点而不落下来,求:
(1)小球至少应从多高处开始滑下?(提示:使用动能定理或机械能守恒定律)
(2)通过轨道点最低点时球对轨道压力多大?已知离心圆轨道半径为R,(不计各处摩擦。)
1. WG= E重
3. W合= EK
2. W弹= E弹
力学领域中功能关系的主要形式:
4.功 能 原 理:
其他力对物体所做的功(重力、弹力以外的力)等于物体机械能的变化:
a.当W其他>0时,△E机>0,机械能增加
b.当W其他<0时,△E机<0,机械能减少
5.系统克服摩擦力所做的总功等于系统机械能的减少量,滑动摩擦力与相对距离(或路程)的乘积在数值上等于系统产生的内能,即:
6.只有重力或弹力做功的系统,系统机械能守恒,即:
【例题4】
1、功 能 原 理:
其他力对物体所做的功(重力、弹力以外的力)等于物体机械能的变化:
请问:重力、弹力对物体做功其机械能是否发生变化?
答案:
机械能守恒定律告诉我们,在只有重力或弹力做功的物体系统内,机械能守恒。
功和能
功
功:W=FScos (只适用恒力做功)
功率:
能
动能:
势能:
Ep ′=1/2 kx2
机械能:E=EP+EK=mgh+1/2 mv2
功能关系
功是能量转化的量度——W其他=△E
动能定理
机械能守恒定律
摩擦力做功
1.摩擦力做功与路径有关。
2.静摩擦力、滑动摩擦力均可以做正功,也可以做负功,还可以不做功。
3.一对静摩擦力所做总功恒为零。
4.一对滑动摩擦力所做总功恒为负。
5.静摩擦力做功过程中,只有机械能的相互转移,没有机械能转化为其它形式的能。
6.滑动摩擦力做功的过程中,可以是产生摩擦力的物体间机械能的转移,也可以是机械能转化为内能.【 】
摩擦力的做功特点
与对应形式能量转化之间的关系:
名称 计算公式 做功特点与能量转换关系
1、作用力和反作用力做功情况没有必然联系;
2、一对相互作用的力,作用力对物体做功,反作用力不一定对物体做功;
3、作用力对物体做正功,反作用力不一定做负功;
温馨提示:请做笔记!
能量形式 涵 义 实 例
机械能 机械能是与物体的运动或位置的高度、形变相关的能量,表现为动能和势能。 流动的河水、被拉开的弓、声音等
内能 内能是组成物体的分子的无规则运动所具有的动能和势能的总和 一切由分子构成的物质
电能 电能是与电有关的能量 电器设备所消耗的的能量都是电能
电磁能 电磁能是以各种各样的电磁波的形式传播的能量 可见光、紫外线、微波和红外线等
核能 核能是一种储存在原子核内部的能量,原子核发生核反应时,会释放出巨大的能量 核潜艇、核电站、核武器等
化学能 化学能是指储存在化合物的化学键里的能量 巧克力、燃料等都储存有化学能
各种各样的能量
1、能量守恒定律的内容:
2、导致能量守恒定律最后确立的两类重要事实是什么
导致能量守恒定律最后确立的两类重要事实是确立了永动机的不可能性和发现了各种自然现象之间的相互联系与转化.
⑴、内容:
能量既不会凭空产生,也不会凭空消失,它只能从一种形式转化为另一种形式,或者从一个物体转移到另一个物体,而在转化或转移过程中,其总量保持不变.
⑵、定律的表达式
E初=E末 ;△E增=△E减
人们还提出过利用轮子的惯性、细管子的毛细作用、 电磁力、流水等获得有效动力的种种永动机设计方案,但都无一例外地失败了,17~18世纪许多机械专家就已经论证了永动机是不可能的。
法国科学院在1775年就正式决定,不再研究和试验任何永动机!
历史上有很多人不相信能量守恒定律的人,挖空心思想发明一种不消耗能量,却能不断对外做功的机器——永动机
永动不可能制成的原因 :
根据能量守恒定律,任何一部机器,只能使能量从一种形式转化为另一种形式,而不能无中生有地制造能量,因此第一类永动机是不可能制成的.
燃料燃烧时一旦把自己的热量释放出去,它就不会自动聚集起来供人类重新利用。(能量转化的方向性)
电池中的化学能转化为电能,它又通过灯泡转化成内能和光能,热和光被其他物质吸收后变为周围环境的内能,我们无法把这些内能收集起来重新利用.这种现象叫做能量的耗散.
内能总是自发地从高温物体向低温物体转移,而不会自发的由低温物体向高温物体转移.
刚煮好的鸡蛋放入凉水中
(内能: 鸡蛋 凉水)
1、机械能可以全部转化为内能;
(举例:在粗糙地面上木块由运动到静止的过程)
2、而内能不可全部转化为机械能而不引起其他变化;
热机的效率不可能100%(第二类永动机不可能存在)
(热机是指各种利用内能做功的机械,如蒸汽机、汽轮机、燃气轮机、内燃机、喷气发动机等)
例如:一辆行驶的小轿车,燃料燃烧产生的内能有370/0通过发动机散热系统排出,370/0直接由排气管排出,有260/0变为发动机输出的机械能
