人教版数学九年级下册:27.1章前引言及相似图形 学案(无答案)
文档属性
| 名称 | 人教版数学九年级下册:27.1章前引言及相似图形 学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 00:00:00 | ||
图片预览


文档简介
27.1图形的相似 学案
学习目标:
1、通过对事物的图形的观察、思考与分析,认识理解相似的图形。
2、通过与全等图形的类比,分析得出相似多边形的性质与判定方法,从而学会用相似边形性质求角度与边长,用判定方法判定相似。
3、经历动手操作的活动过程,增强学生的观察、动手能力。
4、体会图形的相似在现实世界中的存在与运用,进一步提高学生数学应用意识。
重点难点:
重点:认识图形的相似、形成图形相似的概念,掌握相似多边形的性质与判定方法,并会应用。
难点:相似多边形性质的探索过程
一、复习
1、能够 两个图形是全等图形。也就是说形状 ,大小 的两图形是全等的。
2、全等多边形的性质:对应角 ,对应边 。
二、预习书本27.1图形的相似,思考完成以下问题
1、两个边长均为2㎝的等边三角形,它们全等吗?
2、如果两个等边三角形均不知道边长是多少,这时,它们还全等吗?如果不全等,它们是什么关系?
3、(相似定义)我们把 的图形叫相似图形。
4、下列图形相似吗?你为什么这样认为?
请再举两个生活中存在的相似的例子:
(1)、
(2)、
5、两个相似图形,其中一个可以看作由另一个 得到。
思考:一开始我们研究的边长均为2㎝的两个等边三角形是不是相似图形?说说你的看法。
我认为这两个等边三角形
因为
探究1、
1.如图的△A1B1C1是由等边△ABC放大后得到的,观察这两个图形,你认为它们是什么关系?它们的对应角分别是多少度,有什么关系?对应边分别多长,有什么关系呢?
∵△ABC、△A1B1C1都是等边三角形
∴= , = ,= ,
= ,= ,= ,
∴
∵△ABC、△A1B1C1都是等边三角形
∴=== ,===
∴
所以,等边三角形都相似,它们的对应角 ,对应边
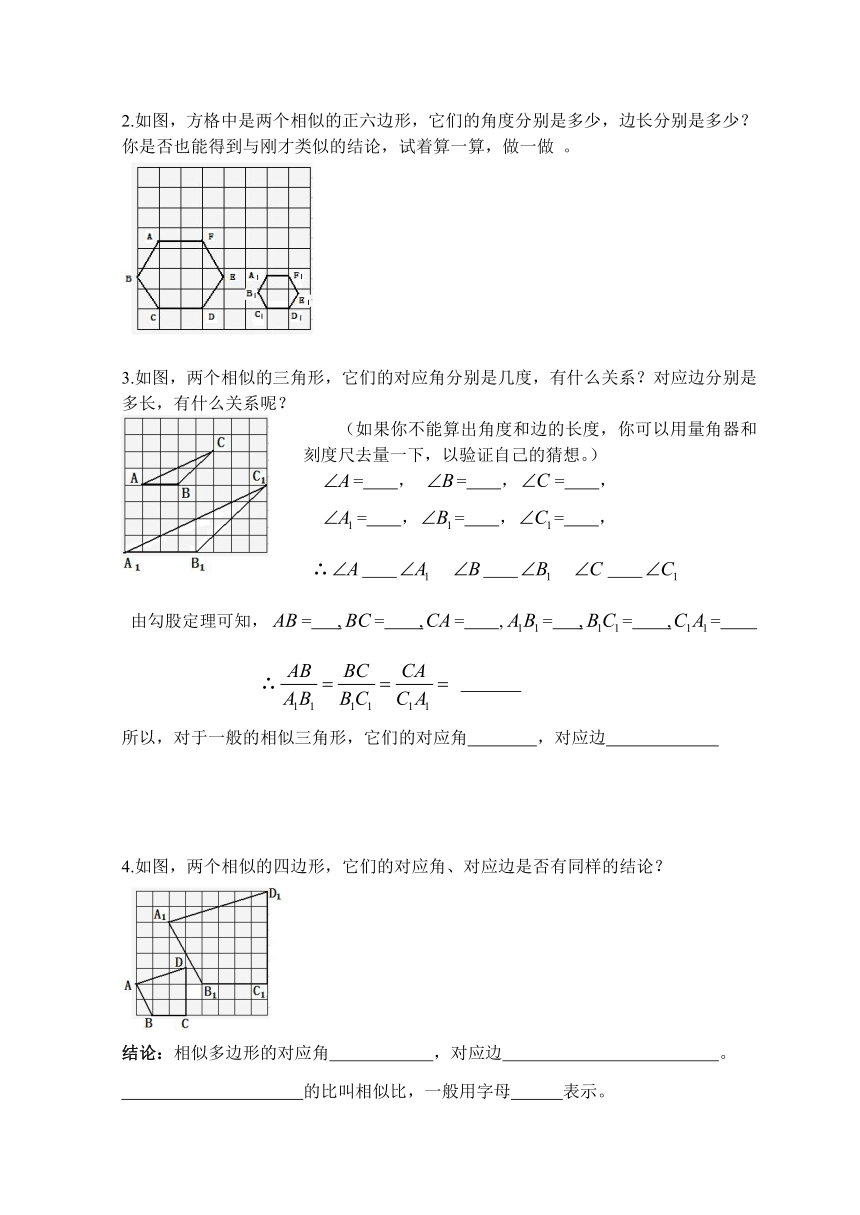
2.如图,方格中是两个相似的正六边形,它们的角度分别是多少,边长分别是多少?你是否也能得到与刚才类似的结论,试着算一算,做一做 。
3.如图,两个相似的三角形,它们的对应角分别是几度,有什么关系?对应边分别是多长,有什么关系呢?
(如果你不能算出角度和边的长度,你可以用量角器和刻度尺去量一下,以验证自己的猜想。)
= , = ,= ,
= ,= ,= ,
∴
由勾股定理可知,= ,= ,= ,= ,= ,=
∴
所以,对于一般的相似三角形,它们的对应角 ,对应边
4.如图,两个相似的四边形,它们的对应角、对应边是否有同样的结论?
结论:相似多边形的对应角 ,对应边 。
的比叫相似比,一般用字母 表示。
探究2、
思考1:如果两个多边形角对应相等,那么它们相似吗?为什么?请举例说明。
思考2:如果两个多边形对应边的比相等,那么它们相似吗?为什么?请举例说明。
结论:只有当两个多边形对应角 ,对应边 ,那么我们才说这两个多边形相似。
练习.如图,在4×4的正方形网格上,有一△ABC。
现要求再画一△A’B’C’,使这两个三角形相似
(要求顶点均在格点上)。
你能证明你所画的△A’B’C’与原△ABC相似吗?(课后思考并完成)
课堂检测:
1、下图中的哪组图形是相似图形 ( )
2、如图所示,左侧上海名牌大众汽车的标志图案,与右侧A、B、C、D四个图形中相似的是( )
3、下列是相似图形的有( )
A. 两个三角形 B. 两个正方形
C. 两个直角三角形 D. 两个矩形
4.、如图,四边形与四边形相似,求,,,的度数以及线段的长
5、如图,作出与方格纸中的图形相似的图形,使点A与A′对应,且所画的图形是原图形的2倍。
学习目标:
1、通过对事物的图形的观察、思考与分析,认识理解相似的图形。
2、通过与全等图形的类比,分析得出相似多边形的性质与判定方法,从而学会用相似边形性质求角度与边长,用判定方法判定相似。
3、经历动手操作的活动过程,增强学生的观察、动手能力。
4、体会图形的相似在现实世界中的存在与运用,进一步提高学生数学应用意识。
重点难点:
重点:认识图形的相似、形成图形相似的概念,掌握相似多边形的性质与判定方法,并会应用。
难点:相似多边形性质的探索过程
一、复习
1、能够 两个图形是全等图形。也就是说形状 ,大小 的两图形是全等的。
2、全等多边形的性质:对应角 ,对应边 。
二、预习书本27.1图形的相似,思考完成以下问题
1、两个边长均为2㎝的等边三角形,它们全等吗?
2、如果两个等边三角形均不知道边长是多少,这时,它们还全等吗?如果不全等,它们是什么关系?
3、(相似定义)我们把 的图形叫相似图形。
4、下列图形相似吗?你为什么这样认为?
请再举两个生活中存在的相似的例子:
(1)、
(2)、
5、两个相似图形,其中一个可以看作由另一个 得到。
思考:一开始我们研究的边长均为2㎝的两个等边三角形是不是相似图形?说说你的看法。
我认为这两个等边三角形
因为
探究1、
1.如图的△A1B1C1是由等边△ABC放大后得到的,观察这两个图形,你认为它们是什么关系?它们的对应角分别是多少度,有什么关系?对应边分别多长,有什么关系呢?
∵△ABC、△A1B1C1都是等边三角形
∴= , = ,= ,
= ,= ,= ,
∴
∵△ABC、△A1B1C1都是等边三角形
∴=== ,===
∴
所以,等边三角形都相似,它们的对应角 ,对应边
2.如图,方格中是两个相似的正六边形,它们的角度分别是多少,边长分别是多少?你是否也能得到与刚才类似的结论,试着算一算,做一做 。
3.如图,两个相似的三角形,它们的对应角分别是几度,有什么关系?对应边分别是多长,有什么关系呢?
(如果你不能算出角度和边的长度,你可以用量角器和刻度尺去量一下,以验证自己的猜想。)
= , = ,= ,
= ,= ,= ,
∴
由勾股定理可知,= ,= ,= ,= ,= ,=
∴
所以,对于一般的相似三角形,它们的对应角 ,对应边
4.如图,两个相似的四边形,它们的对应角、对应边是否有同样的结论?
结论:相似多边形的对应角 ,对应边 。
的比叫相似比,一般用字母 表示。
探究2、
思考1:如果两个多边形角对应相等,那么它们相似吗?为什么?请举例说明。
思考2:如果两个多边形对应边的比相等,那么它们相似吗?为什么?请举例说明。
结论:只有当两个多边形对应角 ,对应边 ,那么我们才说这两个多边形相似。
练习.如图,在4×4的正方形网格上,有一△ABC。
现要求再画一△A’B’C’,使这两个三角形相似
(要求顶点均在格点上)。
你能证明你所画的△A’B’C’与原△ABC相似吗?(课后思考并完成)
课堂检测:
1、下图中的哪组图形是相似图形 ( )
2、如图所示,左侧上海名牌大众汽车的标志图案,与右侧A、B、C、D四个图形中相似的是( )
3、下列是相似图形的有( )
A. 两个三角形 B. 两个正方形
C. 两个直角三角形 D. 两个矩形
4.、如图,四边形与四边形相似,求,,,的度数以及线段的长
5、如图,作出与方格纸中的图形相似的图形,使点A与A′对应,且所画的图形是原图形的2倍。
