18.1勾股定理
图片预览



文档简介
(共34张PPT)
毕达哥拉斯,(公元前572-前492年) ,古希腊著名的数学家、哲学家、天文学家。
毕达哥拉斯
A
B
C
SA+SB=SC
a
a
c
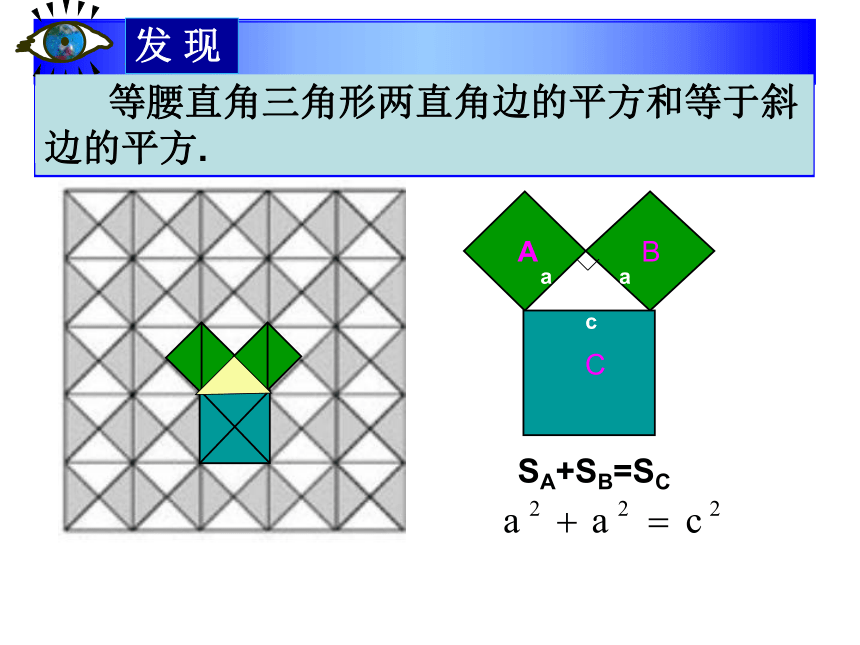
1.在这张图中,你发现了哪些基本图形
2.毕达哥拉斯发现了与三角形相邻的正方形面积有一种特殊的关系.你发现了吗
3.从而毕达哥拉斯就得出了等腰直角三角形三边的某种数量关系.你觉得是什么关系
发 现
等腰直角三角形两直角边的平方和等于斜边的平方.
B
A
C
图3
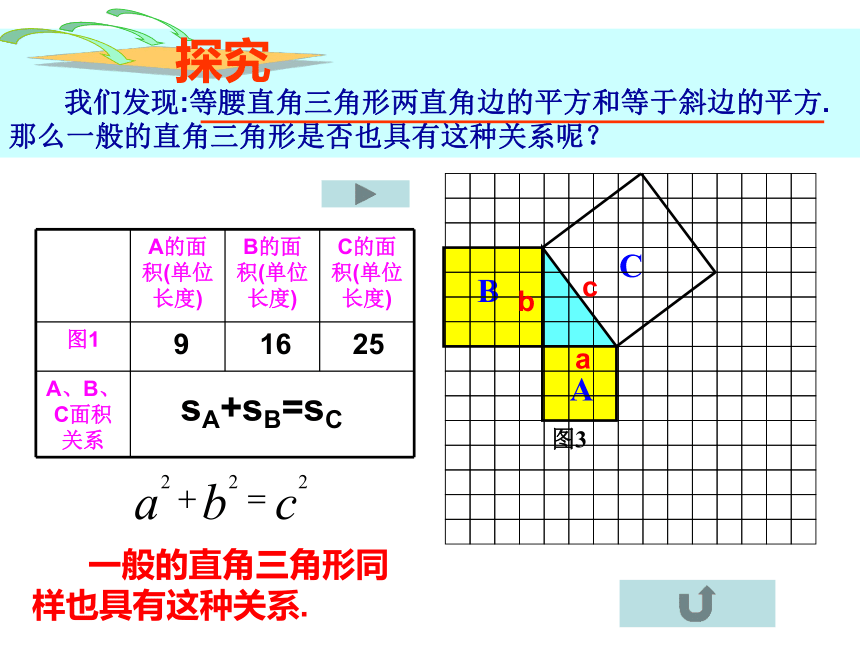
我们发现:等腰直角三角形两直角边的平方和等于斜边的平方.那么一般的直角三角形是否也具有这种关系呢?
探究
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图1
A、B、C面积关系
9
16
25
sA+sB=sC
一般的直角三角形同样也具有这种关系.
a
b
c
B
A
C
图3
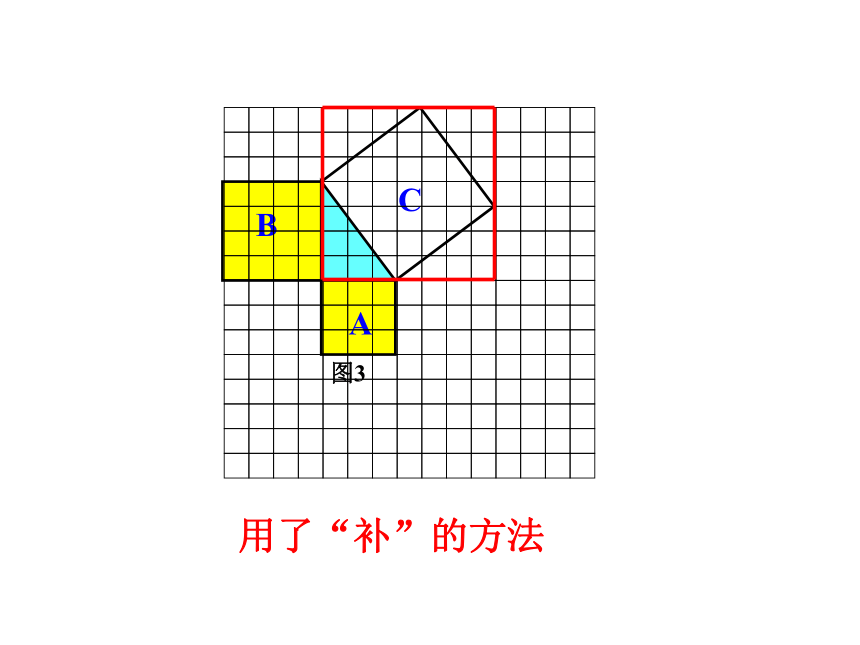
用了“补”的方法
B
A
C
图3
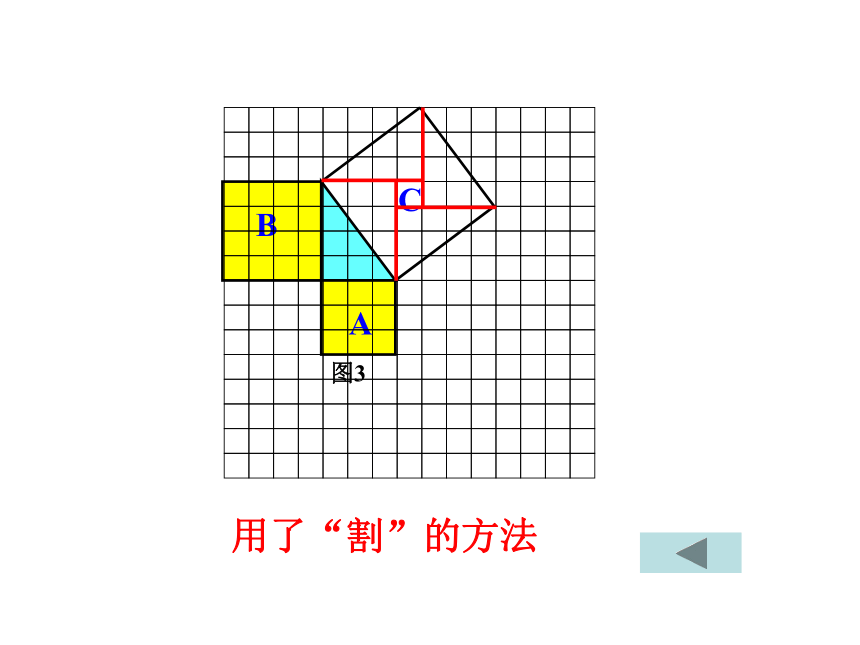
用了“割”的方法
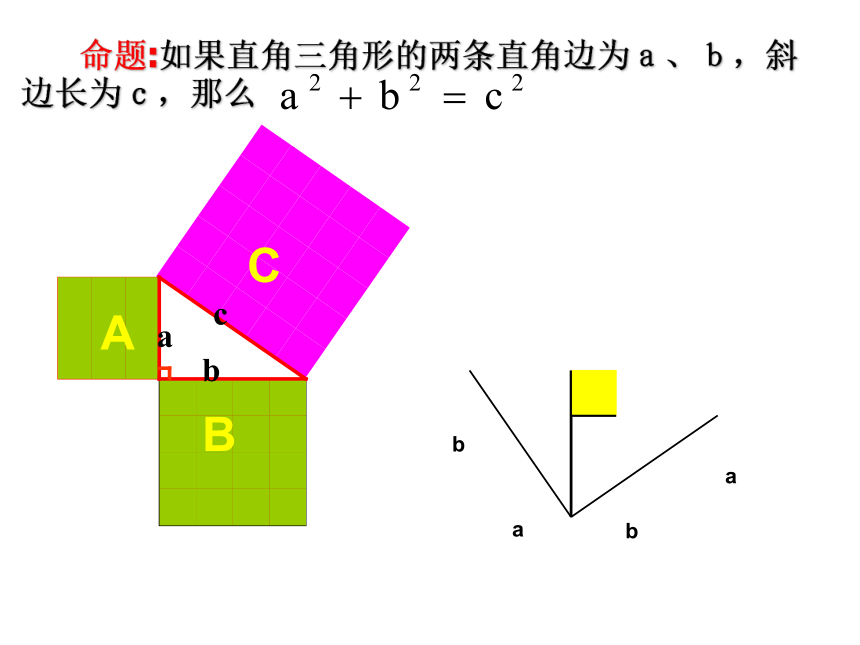
命题:如果直角三角形的两条直角边为a、b,斜边长为c,那么
C
A
B
c
a
b
b
b
a
a
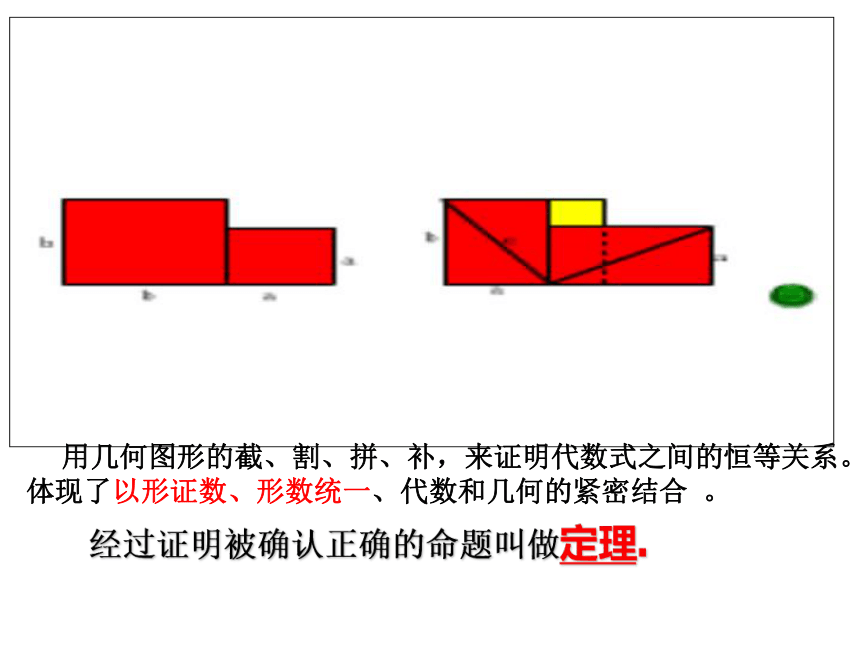
经过证明被确认正确的命题叫做定理.
用几何图形的截、割、拼、补,来证明代数式之间的恒等关系。体现了以形证数、形数统一、代数和几何的紧密结合 。
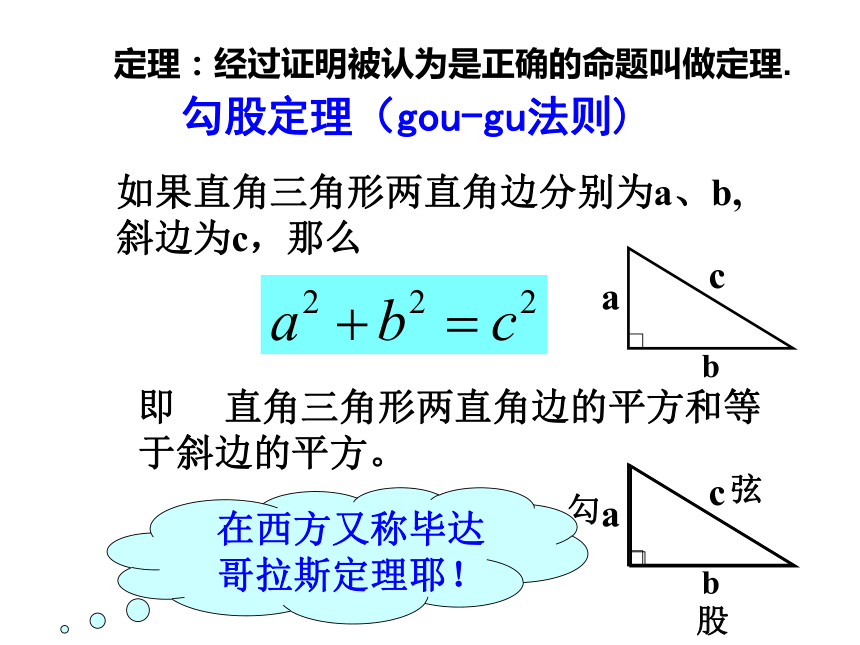
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
勾
股
弦
在西方又称毕达哥拉斯定理耶!
勾股定理(gou-gu法则)
a
b
c
a
b
c
定理:经过证明被认为是正确的命题叫做定理.
勾股定理有着悠久的历史,几乎所有具有古代文化的民族和国家都对勾股定理有所了解,它来源于人们生产实践之中,对人类发展起着十分重要的作用。
我国著名数学家华罗庚曾建议“发射”一种勾股定理的图形到宇宙中,如果宇宙有人的话,他们一定会认识这种语言的。这条建议得到许多科学家的赞同。
勾股定理 外星人
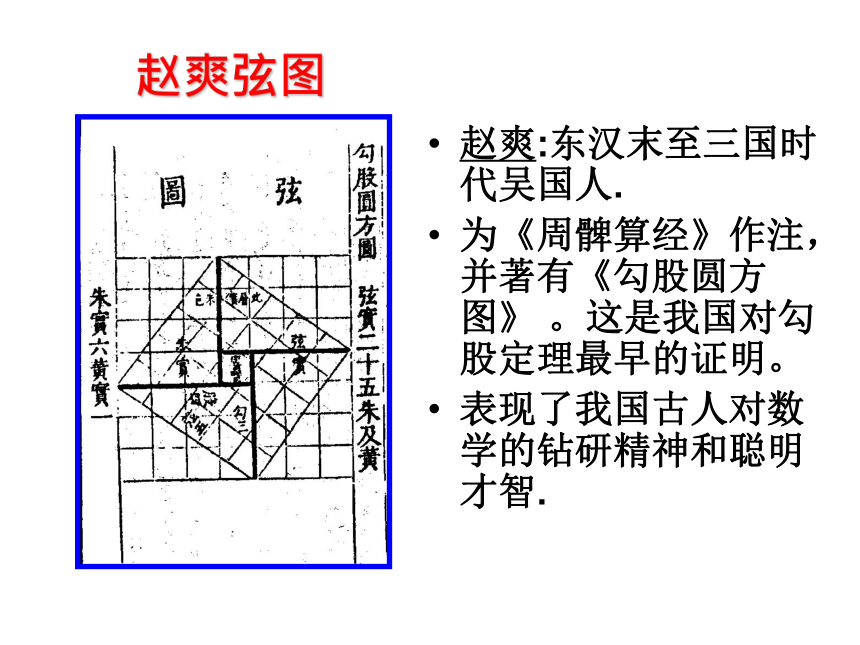
赵爽弦图
赵爽:东汉末至三国时代吴国人.
为《周髀算经》作注,并著有《勾股圆方图》 。这是我国对勾股定理最早的证明。
表现了我国古人对数学的钻研精神和聪明才智.
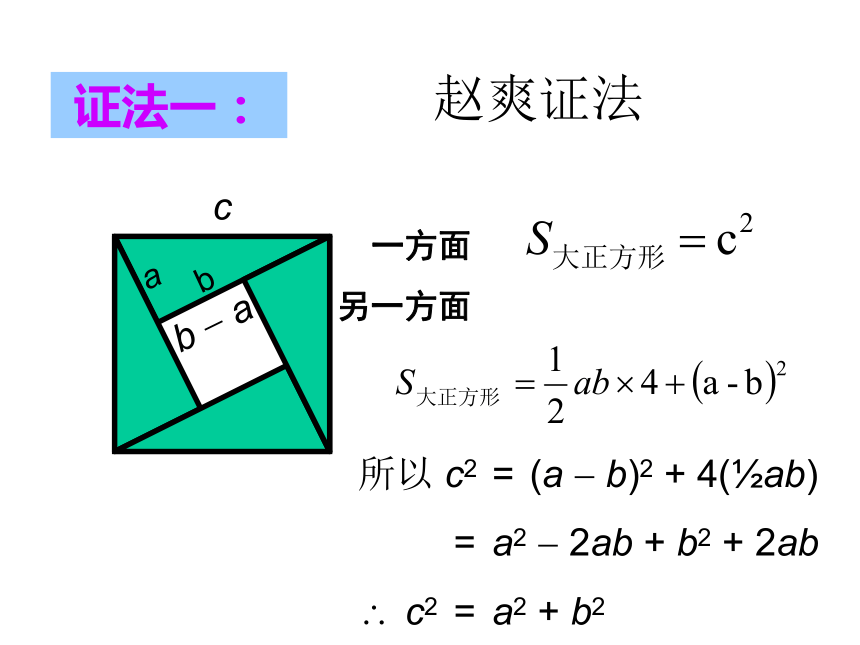
赵爽证法
c
b a
所以 c2 = (a b)2 + 4( ab)
= a2 2ab + b2 + 2ab
c2 = a2 + b2
a
b
证法一:
一方面
另一方面
2002年世界数学家大会在北京召开,这届大会会标的中央图案正是经过艺术处理的“弦图”,标志着中国古代数学成就。
在西方,勾股定理又被称为“毕达哥拉斯定理”, “百牛定理”, “驴桥定理”.
一方面
另一方面
a
a
a
a
b
b
b
b
c
c
c
c
拼一拼
你还能用4个全等的直角三角形拼图说明勾股定理吗
∴
证法二:
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第二十任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。
证法三:
伽菲尔德证法:
∴ a2 + b2 = c2
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
青朱出入图
朱入
朱出
拼图游戏
达芬奇证明方法
试一试
例1:求下图中字母A、B所代表的正方形的面积.
81
144
B
A
25
16
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
3、求出下列直角三角形中未知边的长度
6
8
x
5
x
13
解:(1)∵∠C=90°
∴ AB2=AC2+BC2
∴ x2=62+82 =36+64 =100
∵x>0 ∴x=10
∴ x2+52=132
∴ x2=132-52=169-25=144
A
B
C
A
B
C
解:(2)∵∠C=90°
∴ AB2=AC2+BC2
∵x>0 ∴x=12
4.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
1
1
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
5 或
2、已知:Rt△ABC中,AB=4,AC=3,则BC的长为___________ .
试一试:
4
3
A
C
B
4
3
C
A
B
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A 2、4、6
C 4、6、8
B
试一试:
B 6、8、10
D 8、10、12
4、湖的两端有A、B两点,从与BA方向成直角的公元前方向上的点C测得CA=130米,CB=120米,则AB为( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
A
B
C
D
7cm
5.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
1、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
×
×
1、本节课我们经历了怎样的探究过程?
2、本节课我们学到了什么?
3、学了本节课后我们有什么感想?
梳理反思:
从特殊----- 一般的探究过程
勾股定理 割补法 以形解数法
中国悠久的文化和伟大的古代文明
毕达哥拉斯,(公元前572-前492年) ,古希腊著名的数学家、哲学家、天文学家。
毕达哥拉斯
A
B
C
SA+SB=SC
a
a
c
1.在这张图中,你发现了哪些基本图形
2.毕达哥拉斯发现了与三角形相邻的正方形面积有一种特殊的关系.你发现了吗
3.从而毕达哥拉斯就得出了等腰直角三角形三边的某种数量关系.你觉得是什么关系
发 现
等腰直角三角形两直角边的平方和等于斜边的平方.
B
A
C
图3
我们发现:等腰直角三角形两直角边的平方和等于斜边的平方.那么一般的直角三角形是否也具有这种关系呢?
探究
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图1
A、B、C面积关系
9
16
25
sA+sB=sC
一般的直角三角形同样也具有这种关系.
a
b
c
B
A
C
图3
用了“补”的方法
B
A
C
图3
用了“割”的方法
命题:如果直角三角形的两条直角边为a、b,斜边长为c,那么
C
A
B
c
a
b
b
b
a
a
经过证明被确认正确的命题叫做定理.
用几何图形的截、割、拼、补,来证明代数式之间的恒等关系。体现了以形证数、形数统一、代数和几何的紧密结合 。
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
勾
股
弦
在西方又称毕达哥拉斯定理耶!
勾股定理(gou-gu法则)
a
b
c
a
b
c
定理:经过证明被认为是正确的命题叫做定理.
勾股定理有着悠久的历史,几乎所有具有古代文化的民族和国家都对勾股定理有所了解,它来源于人们生产实践之中,对人类发展起着十分重要的作用。
我国著名数学家华罗庚曾建议“发射”一种勾股定理的图形到宇宙中,如果宇宙有人的话,他们一定会认识这种语言的。这条建议得到许多科学家的赞同。
勾股定理 外星人
赵爽弦图
赵爽:东汉末至三国时代吴国人.
为《周髀算经》作注,并著有《勾股圆方图》 。这是我国对勾股定理最早的证明。
表现了我国古人对数学的钻研精神和聪明才智.
赵爽证法
c
b a
所以 c2 = (a b)2 + 4( ab)
= a2 2ab + b2 + 2ab
c2 = a2 + b2
a
b
证法一:
一方面
另一方面
2002年世界数学家大会在北京召开,这届大会会标的中央图案正是经过艺术处理的“弦图”,标志着中国古代数学成就。
在西方,勾股定理又被称为“毕达哥拉斯定理”, “百牛定理”, “驴桥定理”.
一方面
另一方面
a
a
a
a
b
b
b
b
c
c
c
c
拼一拼
你还能用4个全等的直角三角形拼图说明勾股定理吗
∴
证法二:
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第二十任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。
证法三:
伽菲尔德证法:
∴ a2 + b2 = c2
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
青朱出入图
朱入
朱出
拼图游戏
达芬奇证明方法
试一试
例1:求下图中字母A、B所代表的正方形的面积.
81
144
B
A
25
16
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
3、求出下列直角三角形中未知边的长度
6
8
x
5
x
13
解:(1)∵∠C=90°
∴ AB2=AC2+BC2
∴ x2=62+82 =36+64 =100
∵x>0 ∴x=10
∴ x2+52=132
∴ x2=132-52=169-25=144
A
B
C
A
B
C
解:(2)∵∠C=90°
∴ AB2=AC2+BC2
∵x>0 ∴x=12
4.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
1
1
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
5 或
2、已知:Rt△ABC中,AB=4,AC=3,则BC的长为___________ .
试一试:
4
3
A
C
B
4
3
C
A
B
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )
A 2、4、6
C 4、6、8
B
试一试:
B 6、8、10
D 8、10、12
4、湖的两端有A、B两点,从与BA方向成直角的公元前方向上的点C测得CA=130米,CB=120米,则AB为( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
A
B
C
D
7cm
5.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
1、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
×
×
1、本节课我们经历了怎样的探究过程?
2、本节课我们学到了什么?
3、学了本节课后我们有什么感想?
梳理反思:
从特殊----- 一般的探究过程
勾股定理 割补法 以形解数法
中国悠久的文化和伟大的古代文明
