8.3实际问题与二元一次方程组(第2课时) 课件(共25张PPT)
文档属性
| 名称 | 8.3实际问题与二元一次方程组(第2课时) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 14:51:35 | ||
图片预览







文档简介
8.3实际问题与二元一次方程组
第二课时
2021年春人教版七年级(下)数学
第八章 二元一次方程组
(1)在对各类应用题的解答过程中,学会构建二元一次方程组的数学模型.
(2)养成自觉反思求解过程和自觉检验方程的解是否正确的良好习惯.
学习目标
上节课我们学习了运用方程组解决一些实际问题,这节课我们继建立二元一次方程组的数学模型解应用题.
探究新知
据统计资料,甲、乙两种作物的单位面积产量的比是 1:2.现要把一块长 200 m、宽 100 m 的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是 3:4?
几何图形问题
探究新知
这里研究的实际上是长方形的面积分割问题,我们可以画出示意图来帮助自己.
把一个长方形分成两个小长方形,有哪些分割方式?
保持宽不变,把长分成两段;
保持长不变,把宽分成两段.
探究新知
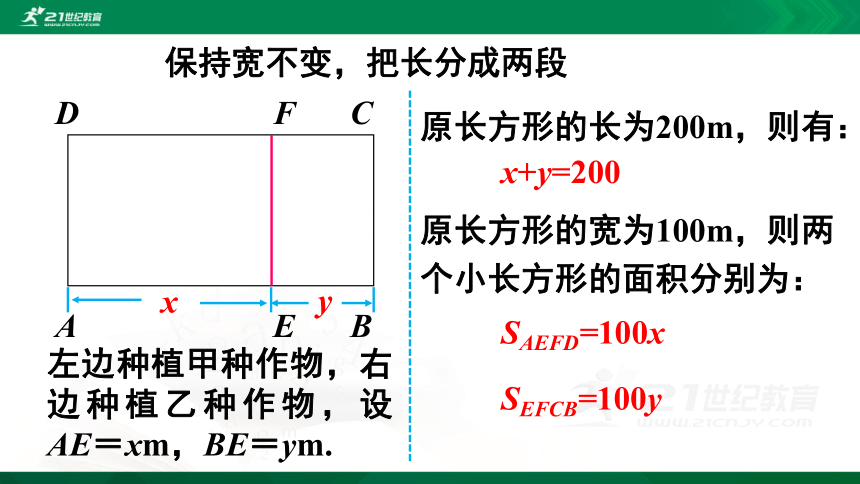
保持宽不变,把长分成两段
左边种植甲种作物,右边种植乙种作物,设AE=xm,BE=ym.
x
y
原长方形的长为200m,则有:
A
D
C
F
B
E
x+y=200
原长方形的宽为100m,则两个小长方形的面积分别为:
SAEFD=100x
SEFCB=100y
A
D
C
F
x
y
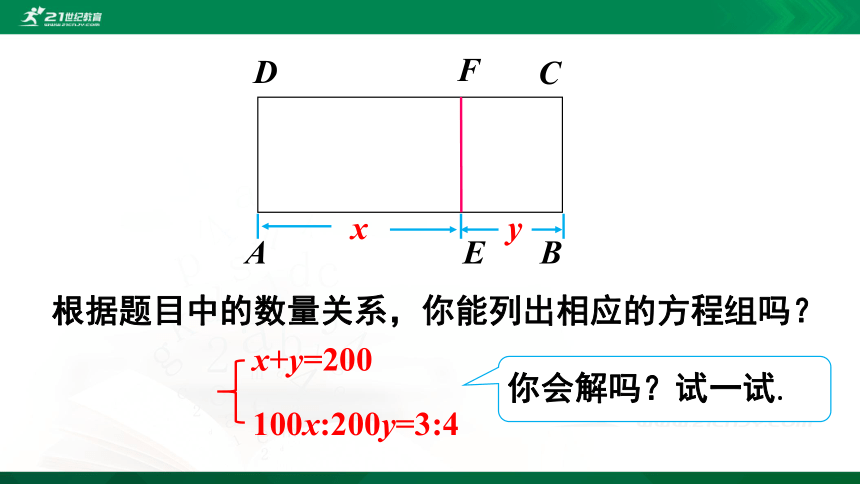
根据题目中的数量关系,你能列出相应的方程组吗?
B
E
x+y=200
100x:200y=3:4
你会解吗?试一试.
x+y=200
100x:200y=3:4
①
②
解:对②移项并化简得:400x=600y
2x=3y ③
联立①③,解得: .
x=120
y=80
过长方形土地的长边上离左端 处,作这条边的垂线,把这块土地分为两块长方形土地.左边较大一块土地种 种作物,右边较小一块土地种 种作物.
x=120
y=80
120m
甲
乙
保持长不变,把宽分成两段
A
D
C
B
x
y
这种情况又要怎么解答呢?
上边种植甲种作物,下边种植乙种作物,设DE=xm,AE=ym.
F
原长方形的宽为100m,则有:
x+y=100
原长方形的长为200m,则两个小长方形的面积分别为:
SAEFB=200y
SEFCD=200x
E
A
D
C
F
x
y
请根据题目中的数量关系,列出相应的方程组.
B
E
x+y=100
200x:400y=3:4
你会解吗?试一试.
x+y=100
200x:400y=3:4
①
②
解:对②移项得:400x=600y
联立①③,解得: .
x=60
y=40
并化简得:2x=3y ③
过长方形土地的长边上离上端 处,作这条边的垂线,把这块土地分为两块长方形土地.上边较大一块土地种 种作物,下边较小一块土地种 种作物.
x=60
y=40
60m
甲
乙
如图①,在边长为 a 的大正方形中剪去一个边长为 b 的小正方形,再将图中的阴影部分剪拼
成一个长方形,如图②.这个拼成的长方形的长为30,宽为20.则图②中Ⅱ部分的面积是 .
故图②中Ⅱ部分的面积是:(a-b)×b
a=25
b=5
解得:
根据边长关系得出:
a+b=30
a-b=20
=20×5
=100
1.如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一块巧克力的质量是 g,一个果冻的质量是 g.
20
30
课堂练习
2.一个长方形的周长为 26,若它的长减少 1,宽增加 2,就变成了一个正方形.设长方形长为 x,宽为 y,则可列方程组为( )
B
A
x+y=26
x-1=y+2
C
26-x=y
x+1=y-2
B
2(x+y)=26
x-1=y+2
D
y+x=13
x+1=y-2
3.如图,宽为 50 cm 的长方形图案由 10 个相同的小长方形拼成,则每个小长方形的长和宽分别是多少?
解:设每个小长方形的宽为 x cm,
长为 y cm.观察图形,得
把①代入②,得 x+4x = 50.解得 x = 10.
把 x = 10 代入①,得 y = 40.
∴这个方程组的解为
答:每个小长方形的长为 40 cm,宽为 10 cm.
4.用含药 30% 和 75% 的两种防腐药水,配制含药 50% 的防腐药水 18 kg,两种药水各需多少千克?
解:设需含药 30% 的药水 x kg,含药 75% 的药水 y kg. 由题意,得
由②,得 10x+25y = 300.③
③-①×10,得 15y = 120. 解得 y = 8.
把 y = 8 代入①. 得 x = 10.
∴这个方程组的解为
答:两种药水各需 10 kg,8 kg.
家具厂有 56 名工人,2 名工人一天可以加工 3 张桌子,3 名工人一天可加工 10 把椅子.现在如何安排劳动力,能使生产的 1 张桌子与 4 把椅子配套?
课堂练习
解:设安排 x 名工人生产桌子,y 名工人生产椅子.
由题意,得
①×5+③,得 14x = 280. 解得 x = 20.
把 x = 20代入①,得 y = 36.
∴这个方程组的解为
答:安排 20 名工人生产桌子,36 名工人生产椅子,可使生产的1张桌子与 4 把椅子配套.
由②得 9x = 5y.③
再见
第二课时
2021年春人教版七年级(下)数学
第八章 二元一次方程组
(1)在对各类应用题的解答过程中,学会构建二元一次方程组的数学模型.
(2)养成自觉反思求解过程和自觉检验方程的解是否正确的良好习惯.
学习目标
上节课我们学习了运用方程组解决一些实际问题,这节课我们继建立二元一次方程组的数学模型解应用题.
探究新知
据统计资料,甲、乙两种作物的单位面积产量的比是 1:2.现要把一块长 200 m、宽 100 m 的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是 3:4?
几何图形问题
探究新知
这里研究的实际上是长方形的面积分割问题,我们可以画出示意图来帮助自己.
把一个长方形分成两个小长方形,有哪些分割方式?
保持宽不变,把长分成两段;
保持长不变,把宽分成两段.
探究新知
保持宽不变,把长分成两段
左边种植甲种作物,右边种植乙种作物,设AE=xm,BE=ym.
x
y
原长方形的长为200m,则有:
A
D
C
F
B
E
x+y=200
原长方形的宽为100m,则两个小长方形的面积分别为:
SAEFD=100x
SEFCB=100y
A
D
C
F
x
y
根据题目中的数量关系,你能列出相应的方程组吗?
B
E
x+y=200
100x:200y=3:4
你会解吗?试一试.
x+y=200
100x:200y=3:4
①
②
解:对②移项并化简得:400x=600y
2x=3y ③
联立①③,解得: .
x=120
y=80
过长方形土地的长边上离左端 处,作这条边的垂线,把这块土地分为两块长方形土地.左边较大一块土地种 种作物,右边较小一块土地种 种作物.
x=120
y=80
120m
甲
乙
保持长不变,把宽分成两段
A
D
C
B
x
y
这种情况又要怎么解答呢?
上边种植甲种作物,下边种植乙种作物,设DE=xm,AE=ym.
F
原长方形的宽为100m,则有:
x+y=100
原长方形的长为200m,则两个小长方形的面积分别为:
SAEFB=200y
SEFCD=200x
E
A
D
C
F
x
y
请根据题目中的数量关系,列出相应的方程组.
B
E
x+y=100
200x:400y=3:4
你会解吗?试一试.
x+y=100
200x:400y=3:4
①
②
解:对②移项得:400x=600y
联立①③,解得: .
x=60
y=40
并化简得:2x=3y ③
过长方形土地的长边上离上端 处,作这条边的垂线,把这块土地分为两块长方形土地.上边较大一块土地种 种作物,下边较小一块土地种 种作物.
x=60
y=40
60m
甲
乙
如图①,在边长为 a 的大正方形中剪去一个边长为 b 的小正方形,再将图中的阴影部分剪拼
成一个长方形,如图②.这个拼成的长方形的长为30,宽为20.则图②中Ⅱ部分的面积是 .
故图②中Ⅱ部分的面积是:(a-b)×b
a=25
b=5
解得:
根据边长关系得出:
a+b=30
a-b=20
=20×5
=100
1.如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一块巧克力的质量是 g,一个果冻的质量是 g.
20
30
课堂练习
2.一个长方形的周长为 26,若它的长减少 1,宽增加 2,就变成了一个正方形.设长方形长为 x,宽为 y,则可列方程组为( )
B
A
x+y=26
x-1=y+2
C
26-x=y
x+1=y-2
B
2(x+y)=26
x-1=y+2
D
y+x=13
x+1=y-2
3.如图,宽为 50 cm 的长方形图案由 10 个相同的小长方形拼成,则每个小长方形的长和宽分别是多少?
解:设每个小长方形的宽为 x cm,
长为 y cm.观察图形,得
把①代入②,得 x+4x = 50.解得 x = 10.
把 x = 10 代入①,得 y = 40.
∴这个方程组的解为
答:每个小长方形的长为 40 cm,宽为 10 cm.
4.用含药 30% 和 75% 的两种防腐药水,配制含药 50% 的防腐药水 18 kg,两种药水各需多少千克?
解:设需含药 30% 的药水 x kg,含药 75% 的药水 y kg. 由题意,得
由②,得 10x+25y = 300.③
③-①×10,得 15y = 120. 解得 y = 8.
把 y = 8 代入①. 得 x = 10.
∴这个方程组的解为
答:两种药水各需 10 kg,8 kg.
家具厂有 56 名工人,2 名工人一天可以加工 3 张桌子,3 名工人一天可加工 10 把椅子.现在如何安排劳动力,能使生产的 1 张桌子与 4 把椅子配套?
课堂练习
解:设安排 x 名工人生产桌子,y 名工人生产椅子.
由题意,得
①×5+③,得 14x = 280. 解得 x = 20.
把 x = 20代入①,得 y = 36.
∴这个方程组的解为
答:安排 20 名工人生产桌子,36 名工人生产椅子,可使生产的1张桌子与 4 把椅子配套.
由②得 9x = 5y.③
再见
