8.3实际问题与二元一次方程组(第3课时) 课件(共25张PPT)
文档属性
| 名称 | 8.3实际问题与二元一次方程组(第3课时) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 14:52:35 | ||
图片预览






文档简介
8.3 实际问题与二元一次方程组
第3课时
第八章 二元一次方程组
2021年春人教版七年级(下)数学
在上两节课的基础上,这节课我们继续来学习用列表分析的方式设未知数,列方程组来解应用题.
新课导入
1.巩固列方程组解应用题的一般步骤.
2.学会用列表的方式分析问题中蕴含的数量关系,并列二元一次方程组.
学习目标
行程问题、工程问题
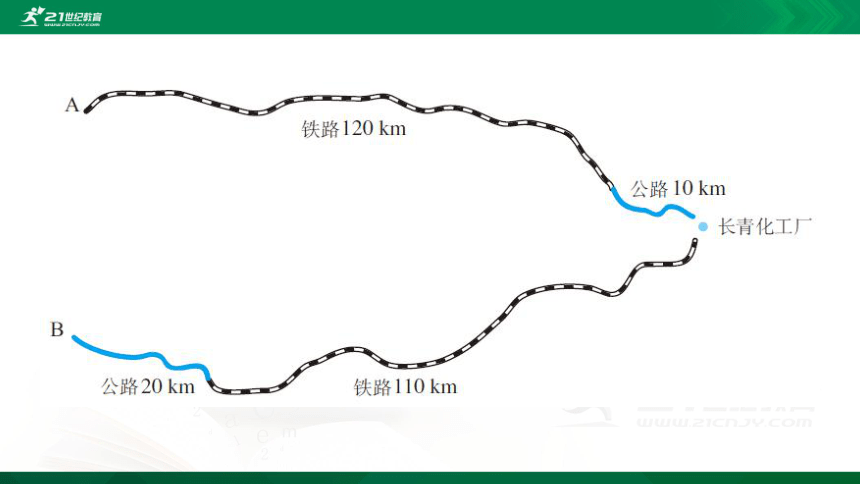
探究3 如图,长青化工厂与 A,B 两地有公路、铁路相连.这家工厂从A地购买一批每吨 1 000元的原料运回工厂,制成每吨 8 000 元的产品运到 B 地.公路运价为 1. 5元/(t·km),铁路运价为 1.2元/(t·km),这两次运输共支出公路运费 15 000 元,铁路运费 97 200 元.这批产品的销售款比原料费与运输费的和多多少元?
探究新知
问题1 要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
问题2 本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
一类是公路运费,铁路运费,价值;
另一类是产品数量,原料数量.
探究新知
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
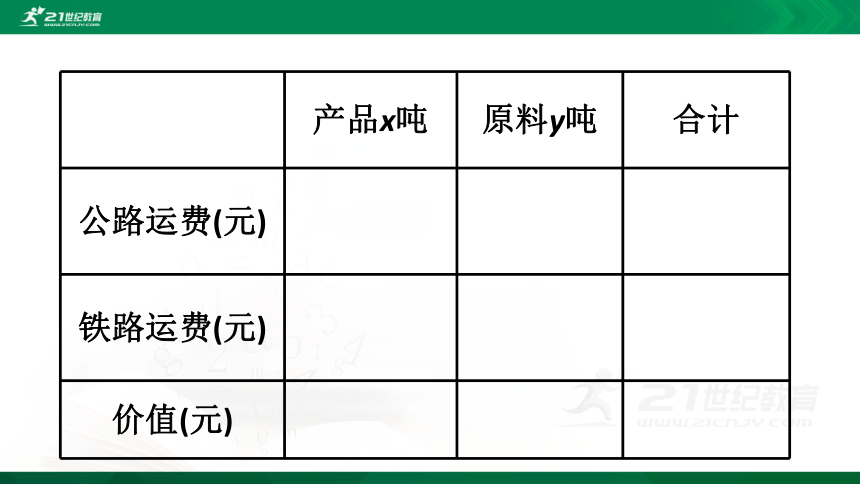
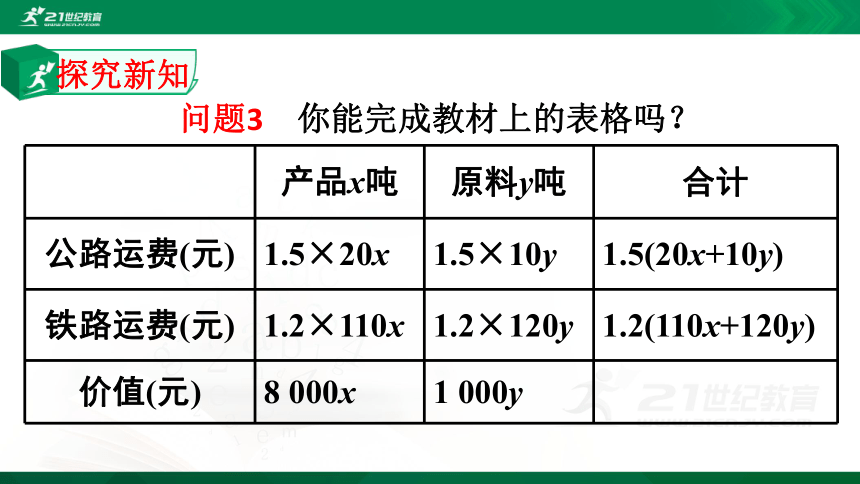
问题3 你能完成教材上的表格吗?
产品x吨
原料y吨
合计
公路运费(元)
1.5×20x
1.5×10y
1.5(20x+10y)
铁路运费(元)
1.2×110x
1.2×120y
1.2(110x+120y)
价值(元)
8 000x
1 000y
探究新知
问题4 你发现等量关系了吗?如何列方程组并求解?
探究新知
是原方程组的解.
解:先化简,得
②
①
由①,得
代入③ ,得
③
代入② ,得
问题5 这个实际问题的答案是什么?
销售款:8 000×300=2 400 000;
原料费:1 000×400=400 000;
运输费:15 000+97 200=112 200.
这批产品的销售款比原料费与运输费的和多1 887 800元.
探究新知
某人要在规定的时间内由甲地赶往乙地,如果他以每小时 50 千米的速度行驶,就会迟到 24 分钟;如果他以每小时 75 千米的速度行驶,则可提前 24 分钟到达乙地,求甲乙两地间的距离.
列方程组时单位不统一
探究新知
错 解
设甲乙两地间的距离为 s 千米,规定时间为 t 小时. 根据题意,得:
解这个方程组,得: .
答:甲乙两地间的距离是 7200 千米.
s=7200
t=120
正 解
设甲乙两地间的距离为 s 千米,规定时间为 t 小时. 根据题意,得:
解这个方程组,得: .
答:甲乙两地间的距离是 120 千米.
s=120
t=2
1.如图,飞腾公司从 A 地购进原料若干吨,加工成产品后销往 B 地.已知公路运费为 1.5元/(t·km),铁路运费为 1 元/(t·km),飞腾公司共支付公路运费 750 元,铁路运费 4000 元.根据以上信息计算:购进原料多少吨?加工后销往 B 地的产品为多少吨?
设购进原料 x t,加工后销往 B 地的产品为 y t.
课堂练习
(1)填表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
数量/t
路程/km
单价/元/(t·km)
运费/元
总运费/元
公路运费/元
购进
销售
铁路运费/元
购进
销售
x
20
1.5
30x
y
10
1.5
15y
750
x
150
1
150x
y
100
1
100y
4000
(2)根据上表中反映的信息列方程组为:
;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
数量/t
路程/km
单价/元/(t·km)
运费/元
总运费/元
公路运费/元
购进
销售
铁路运费/元
购进
销售
x
20
1.5
30x
y
10
1.5
15y
750
x
150
1
150x
y
100
1
100y
4000
(3)解方程组得 ;
(4)答: .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
数量/t
路程/km
单价/元/(t·km)
运费/元
总运费/元
公路运费/元
购进
销售
铁路运费/元
购进
销售
x
20
1.5
30x
y
10
1.5
15y
750
x
150
1
150x
y
100
1
100y
4000
购进原料20t.加工后销往B地的产品为10t
2. A 地至 B 地的航线长 9750 km,一架飞机从A 地顺风飞往 B 地需 12.5 h,它逆风飞行同样的航线需 13 h,求飞机的平均速度与风速.
解:设飞机的平均速度为x km/h,风速为y km/h.
由题意,得 化简,得
①+②,得2x=1530.解得x=765.把x=765代入①,得y=15.
∴这个方程组的解为
3.从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走 3 km,平路每小时走 4 km,下坡每小时走 5 km,那么从甲地到乙地需 54 min,从乙地到甲地需 42 min.甲地到乙地全程是多少?
解:设从甲地 到乙地的上坡路为x km,平路为y km.由题意,得 解得
∴x+y = 3.1.
答:甲地到乙地全程是 3.1 km.
4,打折前,买 60 件 A 商品和 30 件 B 商品用了1 080 元,买 50 件 A 商品和 10 件 B 商品用了 840 元.打折后,买 500 件 A 商品和 500 件 B 商品用了 9 600 元,比不打折少花多少钱?
解:设打折前 A 商品每件 x 元,B 商品每件 y 元.
由题意,得 解得
500x+500y=500×16+500×4=10000.
10000-9600=400(元).答:比不打折少花400元.
实际问题与二元一次方程组(3)
工程、行程问题
题目中涉及的量多
列表分析
发现等量关系
列方程求解
课堂小结
再见
第3课时
第八章 二元一次方程组
2021年春人教版七年级(下)数学
在上两节课的基础上,这节课我们继续来学习用列表分析的方式设未知数,列方程组来解应用题.
新课导入
1.巩固列方程组解应用题的一般步骤.
2.学会用列表的方式分析问题中蕴含的数量关系,并列二元一次方程组.
学习目标
行程问题、工程问题
探究3 如图,长青化工厂与 A,B 两地有公路、铁路相连.这家工厂从A地购买一批每吨 1 000元的原料运回工厂,制成每吨 8 000 元的产品运到 B 地.公路运价为 1. 5元/(t·km),铁路运价为 1.2元/(t·km),这两次运输共支出公路运费 15 000 元,铁路运费 97 200 元.这批产品的销售款比原料费与运输费的和多多少元?
探究新知
问题1 要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
问题2 本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
一类是公路运费,铁路运费,价值;
另一类是产品数量,原料数量.
探究新知
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
问题3 你能完成教材上的表格吗?
产品x吨
原料y吨
合计
公路运费(元)
1.5×20x
1.5×10y
1.5(20x+10y)
铁路运费(元)
1.2×110x
1.2×120y
1.2(110x+120y)
价值(元)
8 000x
1 000y
探究新知
问题4 你发现等量关系了吗?如何列方程组并求解?
探究新知
是原方程组的解.
解:先化简,得
②
①
由①,得
代入③ ,得
③
代入② ,得
问题5 这个实际问题的答案是什么?
销售款:8 000×300=2 400 000;
原料费:1 000×400=400 000;
运输费:15 000+97 200=112 200.
这批产品的销售款比原料费与运输费的和多1 887 800元.
探究新知
某人要在规定的时间内由甲地赶往乙地,如果他以每小时 50 千米的速度行驶,就会迟到 24 分钟;如果他以每小时 75 千米的速度行驶,则可提前 24 分钟到达乙地,求甲乙两地间的距离.
列方程组时单位不统一
探究新知
错 解
设甲乙两地间的距离为 s 千米,规定时间为 t 小时. 根据题意,得:
解这个方程组,得: .
答:甲乙两地间的距离是 7200 千米.
s=7200
t=120
正 解
设甲乙两地间的距离为 s 千米,规定时间为 t 小时. 根据题意,得:
解这个方程组,得: .
答:甲乙两地间的距离是 120 千米.
s=120
t=2
1.如图,飞腾公司从 A 地购进原料若干吨,加工成产品后销往 B 地.已知公路运费为 1.5元/(t·km),铁路运费为 1 元/(t·km),飞腾公司共支付公路运费 750 元,铁路运费 4000 元.根据以上信息计算:购进原料多少吨?加工后销往 B 地的产品为多少吨?
设购进原料 x t,加工后销往 B 地的产品为 y t.
课堂练习
(1)填表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
数量/t
路程/km
单价/元/(t·km)
运费/元
总运费/元
公路运费/元
购进
销售
铁路运费/元
购进
销售
x
20
1.5
30x
y
10
1.5
15y
750
x
150
1
150x
y
100
1
100y
4000
(2)根据上表中反映的信息列方程组为:
;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
数量/t
路程/km
单价/元/(t·km)
运费/元
总运费/元
公路运费/元
购进
销售
铁路运费/元
购进
销售
x
20
1.5
30x
y
10
1.5
15y
750
x
150
1
150x
y
100
1
100y
4000
(3)解方程组得 ;
(4)答: .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
数量/t
路程/km
单价/元/(t·km)
运费/元
总运费/元
公路运费/元
购进
销售
铁路运费/元
购进
销售
x
20
1.5
30x
y
10
1.5
15y
750
x
150
1
150x
y
100
1
100y
4000
购进原料20t.加工后销往B地的产品为10t
2. A 地至 B 地的航线长 9750 km,一架飞机从A 地顺风飞往 B 地需 12.5 h,它逆风飞行同样的航线需 13 h,求飞机的平均速度与风速.
解:设飞机的平均速度为x km/h,风速为y km/h.
由题意,得 化简,得
①+②,得2x=1530.解得x=765.把x=765代入①,得y=15.
∴这个方程组的解为
3.从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走 3 km,平路每小时走 4 km,下坡每小时走 5 km,那么从甲地到乙地需 54 min,从乙地到甲地需 42 min.甲地到乙地全程是多少?
解:设从甲地 到乙地的上坡路为x km,平路为y km.由题意,得 解得
∴x+y = 3.1.
答:甲地到乙地全程是 3.1 km.
4,打折前,买 60 件 A 商品和 30 件 B 商品用了1 080 元,买 50 件 A 商品和 10 件 B 商品用了 840 元.打折后,买 500 件 A 商品和 500 件 B 商品用了 9 600 元,比不打折少花多少钱?
解:设打折前 A 商品每件 x 元,B 商品每件 y 元.
由题意,得 解得
500x+500y=500×16+500×4=10000.
10000-9600=400(元).答:比不打折少花400元.
实际问题与二元一次方程组(3)
工程、行程问题
题目中涉及的量多
列表分析
发现等量关系
列方程求解
课堂小结
再见
