山东泰安肥城市2020-2021学年九年级下学期期中教学质量监测数学试题(word版 含答案)
文档属性
| 名称 | 山东泰安肥城市2020-2021学年九年级下学期期中教学质量监测数学试题(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 00:00:00 | ||
图片预览


文档简介
山东泰安肥城市2020-2021学年九年级下学期期中教学质量监测
数学试题
注意事项∶
1.答题前请将答题卡密封线内的项目填写清楚,然后将试题答案认真书写(填涂)在答题卡的规定位置,否则作废.
2.本试卷共
8页,考试时间
120
分钟,满分
150
分.
3.
考试结束只交答题卡。
一、选择题(本大题共
12
小题,在每小题给出的四个选项中,只有一个是正确的,把正确答案序号填涂在答题纸相应的位置)
1。-I-2I的相反数为
A.
-2
B.2
C.±2
D.±
2.下列图形既是中心对称图形又是轴对称图形的个数为
A.
1个
B.2个
C.
3个
D.4个
3.下列运算正确的是
A.a4·a2=a8
B.a2+a2=2a4
C.
(a+b)2=a2+b2
D.
(-2a3)
2=4a6
4.如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若
由图①变到图②,不改变的是
主视图
B.左视图和俯视图
C.主视图和俯视图
D.主视图和左视图
5.一元二次方程(x+1)(x-2)=10根的情况是
A.无实数根
B.有两个正根
C.有两个根,且都大于-1
D.有两个根,其中一根大于2
6.如图,点A,B,C,D都在半径为1的⊙O
上,若OA⊥BC,∠CDA=30°,则弦BC的长为
A.2
B.
C.
D.
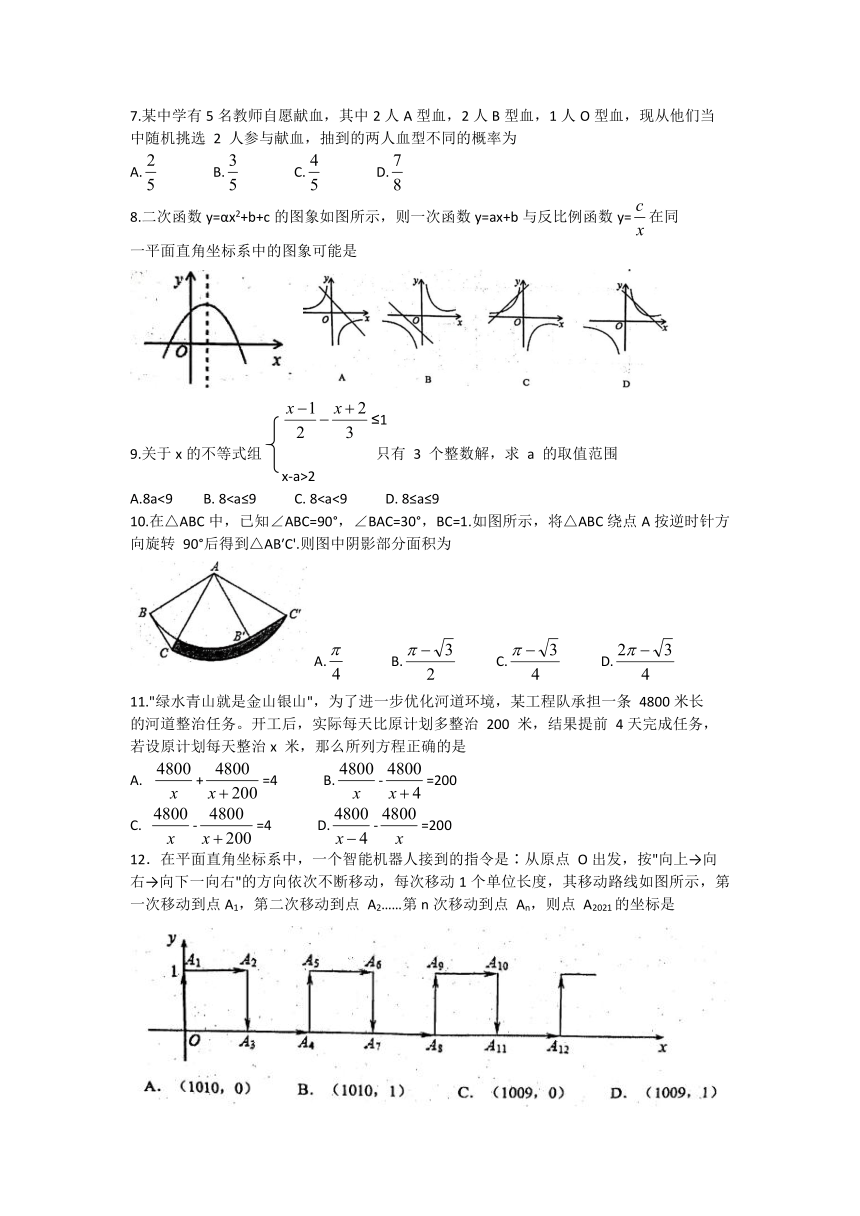
7.某中学有5名教师自愿献血,其中2人A型血,2人B型血,1人O型血,现从他们当
中随机挑选
2
人参与献血,抽到的两人血型不同的概率为
A.
B.
C.
D.
8.二次函数y=αx2+b+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同
一平面直角坐标系中的图象可能是
≤1
9.关于x的不等式组
只有
3
个整数解,求
a
的取值范围
x-a>2
A.8a<9
B.
8C.
8D.
8≤a≤9
10.在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC绕点A按逆时针方向旋转
90°后得到△AB′C'.则图中阴影部分面积为
A.
B.
C.
D.
11."绿水青山就是金山银山",为了进一步优化河道环境,某工程队承担一条
4800米长
的河道整治任务。开工后,实际每天比原计划多整治
200
米,结果提前
4天完成任务,
若设原计划每天整治x
米,那么所列方程正确的是
+=4
B.-=200
C.
-=4
D.-=200
12.在平面直角坐标系中,一个智能机器人接到的指令是∶从原点
O出发,按"向上→向
右→向下一向右"的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点
A2……第n次移动到点
An,则点
A2021的坐标是
填空题(本大题共6小题,满分24分,请将答案直接填写在答题纸相应位置)
13.因式分解∶
x(x-2)-x+2=_
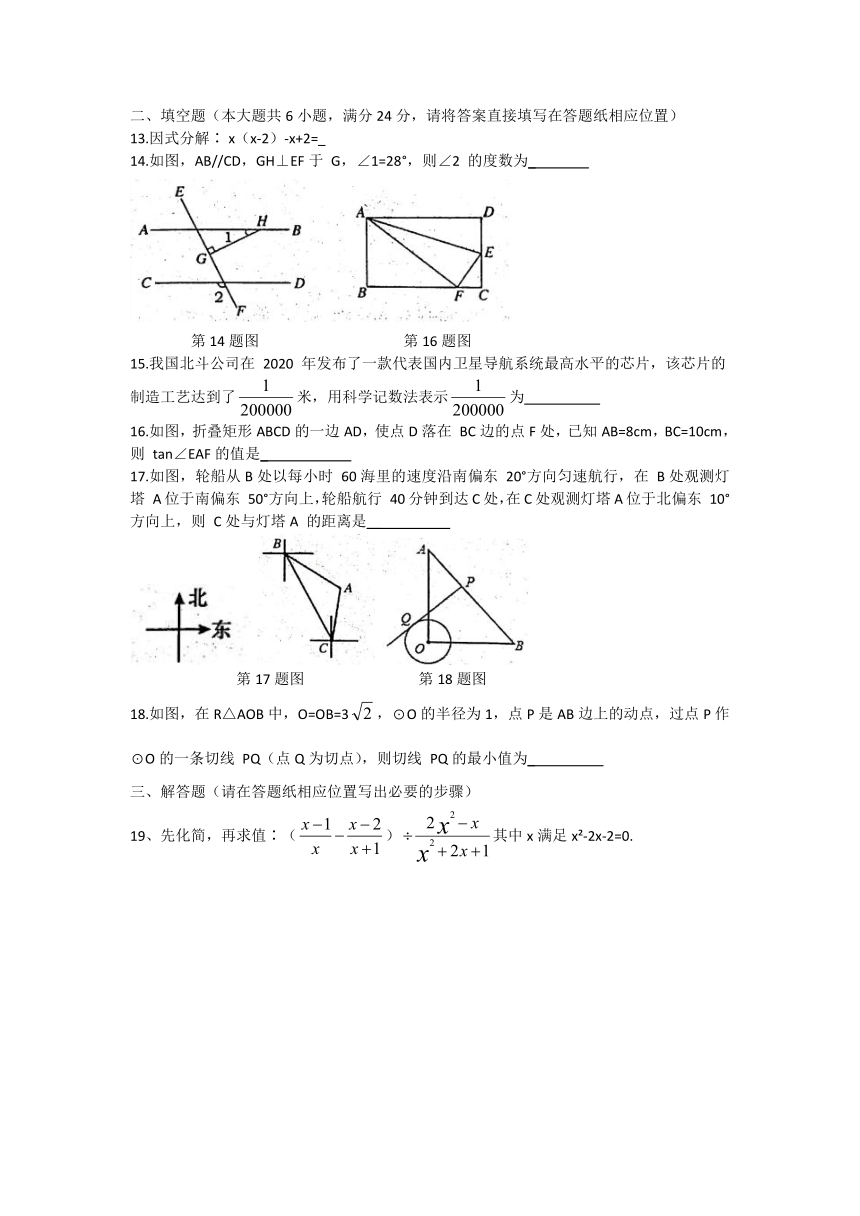
14.如图,AB//CD,GH⊥EF于
G,∠1=28°,则∠2
的度数为_
第14题图
第16题图
15.我国北斗公司在
2020
年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的
制造工艺达到了米,用科学记数法表示为
16.如图,折叠矩形ABCD的一边AD,使点D落在
BC边的点F处,已知AB=8cm,BC=10cm,则
tan∠EAF的值是_
17.如图,轮船从B处以每小时
60海里的速度沿南偏东
20°方向匀速航行,在
B处观测灯塔
A位于南偏东
50°方向上,轮船航行
40分钟到达C处,在C处观测灯塔A位于北偏东
10°方向上,则
C处与灯塔A
的距离是__
第17题图
第18题图
18.如图,在R△AOB中,O=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线
PQ(点Q为切点),则切线
PQ的最小值为_
三、解答题(请在答题纸相应位置写出必要的步骤)
19、先化简,再求值∶()其中x满足x?-2x-2=0.
某学校开展了主题为"垃圾分类,绿色生活新时尚"的宣传活动。为了解学生对垃圾分类知识的掌握情况,学校从全校学生中随机抽取部分学生进行知识测试(测试满分
100分,得分均为整数),并对成绩进行整理、描述和分析部分信息如下∶
a.成绩的扇形统计图与频数分布表∶
b.成绩在
60≤a<70
这一组的是∶
60
62
64
65
66
66
67
67
67
68
69
65
61
63
67
根据以上信息,回答下列问题∶
(1)图表中
m、n的数值分别为多少?所抽取学生成绩在
60≤a<70
这一组的众数是分?
(2)求所抽取学生的平均成绩;
(3)若该校有
1400名学生,假设全部参加此次测试,请估计成绩不低于
80分的人数.
21.如图,已知反比例函数y=的图象经过第二象限内的点
A(-1,m),AB⊥x
轴于点
x
B,△AOB的面积为
2.
若直线y=ax+b经过点,并且经过反比例函数y=的图象上另一点
C(n,-2).
(1)求直线y=ax+b
的解析式;
(2)设直线
y=ax+b与x轴交于点
M,求
AM的长;
(3)在双曲线上是否存在点P,使得△MBP的面积为8?若存在请求P点坐标;若不存在请说明理由。
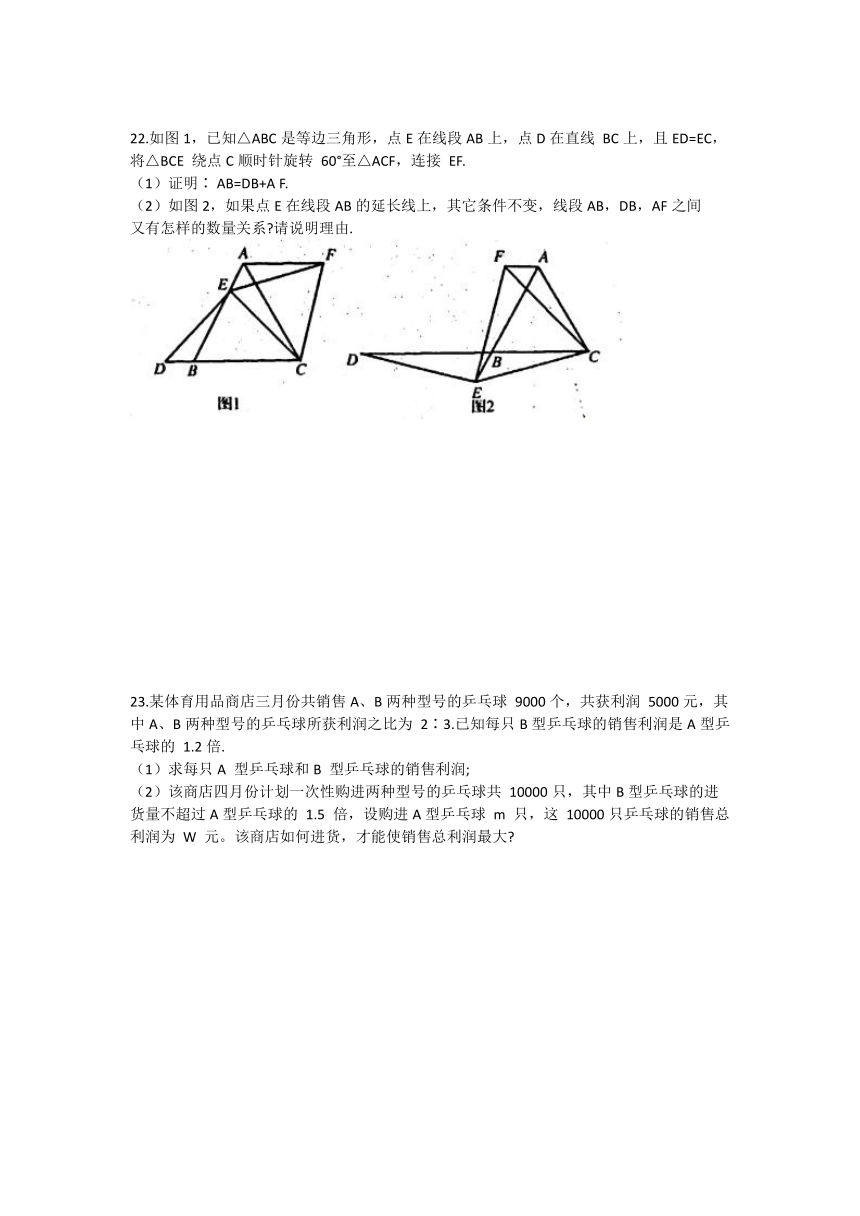
22.如图1,已知△ABC是等边三角形,点E在线段AB上,点D在直线
BC上,且ED=EC,
将△BCE
绕点C顺时针旋转
60°至△ACF,连接
EF.
(1)证明∶
AB=DB+A
F.
(2)如图2,如果点E在线段AB的延长线上,其它条件不变,线段AB,DB,AF之间
又有怎样的数量关系?请说明理由.
23.某体育用品商店三月份共销售A、B两种型号的乒乓球
9000个,共获利润
5000元,其
中A、B两种型号的乒乓球所获利润之比为
2∶3.已知每只B型乒乓球的销售利润是A型乒乓球的
1.2倍.
(1)求每只A
型乒乓球和B
型乒乓球的销售利润;
(2)该商店四月份计划一次性购进两种型号的乒乓球共
10000只,其中B型乒乓球的进
货量不超过A型乒乓球的
1.5
倍,设购进A型乒乓球
m
只,这
10000只乒乓球的销售总利润为
W
元。该商店如何进货,才能使销售总利润最大?
抛物线y=-x?+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,2),直线
CD∶
y=-x+2与x轴交于点D.动点M在抛物线上运动,过点M作MP⊥x轴,垂足为
P,交直线
CD于点
M.
(1)求抛物线的解析式;
(2)如图1,当点P在线段
OD上时,△CDM的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由;
(3)如图2,点E是抛物线对称轴与x轴的交点,点F是x轴上一动点,点M在运动过程中,若以
C、E、F、M为顶点的四边形是平行四边形时,请直接写出点F的坐标。
25.如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN
=45°
(1)如图1,当点M、N分别在线段BC、DC上时,请写出线段BM、MN、DN之间的
数量关系,并说明理由;
(2)如图2,当点M、N分别在
CB、DC的延长线上时,(1)中的结论是否仍然成立,
若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在
CB、DC的延长线上时,若
CN=CD=6,设BD与AM
的延长线交于点P,交AN于Q,直接写出
AQ、AP的长.
数学试题
注意事项∶
1.答题前请将答题卡密封线内的项目填写清楚,然后将试题答案认真书写(填涂)在答题卡的规定位置,否则作废.
2.本试卷共
8页,考试时间
120
分钟,满分
150
分.
3.
考试结束只交答题卡。
一、选择题(本大题共
12
小题,在每小题给出的四个选项中,只有一个是正确的,把正确答案序号填涂在答题纸相应的位置)
1。-I-2I的相反数为
A.
-2
B.2
C.±2
D.±
2.下列图形既是中心对称图形又是轴对称图形的个数为
A.
1个
B.2个
C.
3个
D.4个
3.下列运算正确的是
A.a4·a2=a8
B.a2+a2=2a4
C.
(a+b)2=a2+b2
D.
(-2a3)
2=4a6
4.如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若
由图①变到图②,不改变的是
主视图
B.左视图和俯视图
C.主视图和俯视图
D.主视图和左视图
5.一元二次方程(x+1)(x-2)=10根的情况是
A.无实数根
B.有两个正根
C.有两个根,且都大于-1
D.有两个根,其中一根大于2
6.如图,点A,B,C,D都在半径为1的⊙O
上,若OA⊥BC,∠CDA=30°,则弦BC的长为
A.2
B.
C.
D.
7.某中学有5名教师自愿献血,其中2人A型血,2人B型血,1人O型血,现从他们当
中随机挑选
2
人参与献血,抽到的两人血型不同的概率为
A.
B.
C.
D.
8.二次函数y=αx2+b+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同
一平面直角坐标系中的图象可能是
≤1
9.关于x的不等式组
只有
3
个整数解,求
a
的取值范围
x-a>2
A.8a<9
B.
8
8
8≤a≤9
10.在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC绕点A按逆时针方向旋转
90°后得到△AB′C'.则图中阴影部分面积为
A.
B.
C.
D.
11."绿水青山就是金山银山",为了进一步优化河道环境,某工程队承担一条
4800米长
的河道整治任务。开工后,实际每天比原计划多整治
200
米,结果提前
4天完成任务,
若设原计划每天整治x
米,那么所列方程正确的是
+=4
B.-=200
C.
-=4
D.-=200
12.在平面直角坐标系中,一个智能机器人接到的指令是∶从原点
O出发,按"向上→向
右→向下一向右"的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点
A2……第n次移动到点
An,则点
A2021的坐标是
填空题(本大题共6小题,满分24分,请将答案直接填写在答题纸相应位置)
13.因式分解∶
x(x-2)-x+2=_
14.如图,AB//CD,GH⊥EF于
G,∠1=28°,则∠2
的度数为_
第14题图
第16题图
15.我国北斗公司在
2020
年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的
制造工艺达到了米,用科学记数法表示为
16.如图,折叠矩形ABCD的一边AD,使点D落在
BC边的点F处,已知AB=8cm,BC=10cm,则
tan∠EAF的值是_
17.如图,轮船从B处以每小时
60海里的速度沿南偏东
20°方向匀速航行,在
B处观测灯塔
A位于南偏东
50°方向上,轮船航行
40分钟到达C处,在C处观测灯塔A位于北偏东
10°方向上,则
C处与灯塔A
的距离是__
第17题图
第18题图
18.如图,在R△AOB中,O=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线
PQ(点Q为切点),则切线
PQ的最小值为_
三、解答题(请在答题纸相应位置写出必要的步骤)
19、先化简,再求值∶()其中x满足x?-2x-2=0.
某学校开展了主题为"垃圾分类,绿色生活新时尚"的宣传活动。为了解学生对垃圾分类知识的掌握情况,学校从全校学生中随机抽取部分学生进行知识测试(测试满分
100分,得分均为整数),并对成绩进行整理、描述和分析部分信息如下∶
a.成绩的扇形统计图与频数分布表∶
b.成绩在
60≤a<70
这一组的是∶
60
62
64
65
66
66
67
67
67
68
69
65
61
63
67
根据以上信息,回答下列问题∶
(1)图表中
m、n的数值分别为多少?所抽取学生成绩在
60≤a<70
这一组的众数是分?
(2)求所抽取学生的平均成绩;
(3)若该校有
1400名学生,假设全部参加此次测试,请估计成绩不低于
80分的人数.
21.如图,已知反比例函数y=的图象经过第二象限内的点
A(-1,m),AB⊥x
轴于点
x
B,△AOB的面积为
2.
若直线y=ax+b经过点,并且经过反比例函数y=的图象上另一点
C(n,-2).
(1)求直线y=ax+b
的解析式;
(2)设直线
y=ax+b与x轴交于点
M,求
AM的长;
(3)在双曲线上是否存在点P,使得△MBP的面积为8?若存在请求P点坐标;若不存在请说明理由。
22.如图1,已知△ABC是等边三角形,点E在线段AB上,点D在直线
BC上,且ED=EC,
将△BCE
绕点C顺时针旋转
60°至△ACF,连接
EF.
(1)证明∶
AB=DB+A
F.
(2)如图2,如果点E在线段AB的延长线上,其它条件不变,线段AB,DB,AF之间
又有怎样的数量关系?请说明理由.
23.某体育用品商店三月份共销售A、B两种型号的乒乓球
9000个,共获利润
5000元,其
中A、B两种型号的乒乓球所获利润之比为
2∶3.已知每只B型乒乓球的销售利润是A型乒乓球的
1.2倍.
(1)求每只A
型乒乓球和B
型乒乓球的销售利润;
(2)该商店四月份计划一次性购进两种型号的乒乓球共
10000只,其中B型乒乓球的进
货量不超过A型乒乓球的
1.5
倍,设购进A型乒乓球
m
只,这
10000只乒乓球的销售总利润为
W
元。该商店如何进货,才能使销售总利润最大?
抛物线y=-x?+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,2),直线
CD∶
y=-x+2与x轴交于点D.动点M在抛物线上运动,过点M作MP⊥x轴,垂足为
P,交直线
CD于点
M.
(1)求抛物线的解析式;
(2)如图1,当点P在线段
OD上时,△CDM的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由;
(3)如图2,点E是抛物线对称轴与x轴的交点,点F是x轴上一动点,点M在运动过程中,若以
C、E、F、M为顶点的四边形是平行四边形时,请直接写出点F的坐标。
25.如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN
=45°
(1)如图1,当点M、N分别在线段BC、DC上时,请写出线段BM、MN、DN之间的
数量关系,并说明理由;
(2)如图2,当点M、N分别在
CB、DC的延长线上时,(1)中的结论是否仍然成立,
若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在
CB、DC的延长线上时,若
CN=CD=6,设BD与AM
的延长线交于点P,交AN于Q,直接写出
AQ、AP的长.
同课章节目录
