9.1.2 不等式的性质(第2课时)课件(共38张PPT)
文档属性
| 名称 | 9.1.2 不等式的性质(第2课时)课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-09 07:54:52 | ||
图片预览











文档简介
9.1.2 不等式的性质
第2课时
第九章 不等式与不等式组
2021年春人教版七年级(下)数学
某长方体形状的容器长5cm,宽3cm,高10cm.容器内原有水的高度为3cm,现准备向它继续注水.用V(单位cm3)表示新注入水的体积,写出V的取值范围.
新课导入
(1)能运用不等式的性质对不等式进行变形和解简单的不等式.
(2)知道符号“≥”和“≤”的意义及在数轴上表示不等式的解集时实心点与空心圈的区别.
学习目标
利用不等式的性质解不等式
例1 利用不等式的性质解下列不等式:
(1)x-7>26;(2)3x<2x+1
(3) x>50 (4)-4x>3
探究新知
分析
解不等式,就是借助不等式的性质使不等式逐步化为 x>a 或 x(1)x-7>26
解这个不等式要利用哪个性质?
要利用不等式的性质1.
(1)x-7>26
根据不等式的性质1,不等式两边加7,不等号的方向不变,所以:
x-7+7>26+7
x>33
0
33
用数轴表示为
你能把不等式的解集用数轴表示出来吗?
(2)3x<2x+1
根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以:
3x-2x<2x+1-2x
x<1
用数轴表示为
0
1
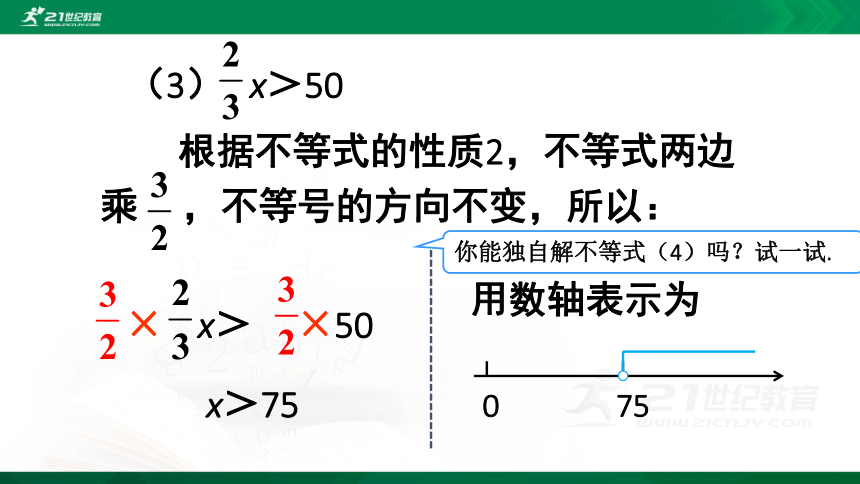
(3) x>50
x>75
根据不等式的性质2,不等式两边乘 ,不等号的方向不变,所以:
× x> ×50
0
75
用数轴表示为
你能独自解不等式(4)吗?试一试.
(4)-4x>3
根据不等式的性质3,不等式两边除以 -4,不等号的方向改变,所以:
用数轴表示为
0
在表示两个数量大小关系时,我们会经常用到像 a≥b 或 a≤b 这样的式子,如一天内的温度变化 t≥19℃ 且 t≤28℃.
符号“≥”与“>”的意思有什么区别?
“≥”表示包含某个数值, “>” 表示不包含该数值.
“≤”表示包含某个数值, “<” 表示不包含该数值.
“≤”与“<”呢?
它们是否具有与前面所说的不等式的性质类似的性质呢?
它们也具有和不等式相同的性质.
如果a≥b,那么a±c≥b±c;
如果a≥b,那么 ac≥bc或 ≥ (其中c>0);
如果a≥b,那么ac≤bc或 ≤ (其中c<0).
归纳小结
1.用不等式的性质解下列不等式,并在数轴上表示出来.
(1)x+5>-1; (2)4x<3x-5;
(3) x< ; (4) -8x>10 .
针对练习
(1)x+5>-1; (2)4x<3x-5;
x>-6
0
-6
4x-3x<3x-5-3x
x+5-5>-1-5
x<-5
0
-5
(3) x< ; (4) -8x>10 .
7× x<7×
x<6
0
6
0
2.用不等式表示下列语句并写出解集,并在数轴上表示解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
3x≥1
x≥
0
x+3≥6
x≥3
0
3
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
y-1≤0
y≤1
0
1
y≤-8
y≤-2
0
-8
不等式的实际应用
某长方体形状的容器长5cm,宽3cm,高10cm.容器内原有水的高度为3cm,现准备向它继续注水.用V(单位cm3)表示新注入水的体积,写出 V 的取值范围.
学习了用不等式的性质解不等式,你现在能解决这个问题了吗?
探究新知
分析
要求新注入水的体积范围,那就要求出容器的总体积和已经被占用的体积.
容器的总体积为:
3×5×10
被占用的容器的体积为:
3×5×3
根据题意有:
V+3×5×3≤3×5×10
V+3×5×3≤3×5×10
V≤105
不是.在利用不等式解决实际问题时一定要考虑未知数的实际意义.
这样就可以了吗?
V+3×5×3≤3×5×10
V≥0且V≤105
考虑到实际意义,新注入水的体积 V 不能是负数,因此 V 的取值范围是:
V≤105
在数轴上表示出来为:
0
105
0
105
这里是实心圆表示,那实心圆与空心圆有什么区别呢?
实心圆表示不等式的取值范围包括这两个数,空心圆表示不等式的取值范围不包括这两个数.
1.解不等式的依据:不等式的性质.
2.在利用不等式的性质解决实际问题时一定要注意未知数的实际意义.
归纳小结
运用不等式的性质3时未改变不等号的方向
解不等式:2-3x>11.
错 解
不等式的两边同减2得-3x>9,
不等式的两边同除以-3得x>-3,
所以原不等式的解集为x>-3.
误区诊断
运用不等式的性质3时未改变不等号的方向
解不等式:2-3x>11.
不等式的两边同减2得-3x>9,
不等式的两边同除以-3得x<-3,
所以原不等式的解集为x<-3.
正 解
误区诊断
错因分析
此题错在没有理解不等式的性质3.在运用不等式的性质3时,不等式的两边乘(或除以)同一个负数,不等号的方向要改变.
1. 不等式3-2x≤7的解集是( )
A.x≥-2 B.x≤-2
C.x≤-5 D.x≥-5
A
课堂练习
2.不等式 x-2≥0 的解集在数轴上表示正确的是( )
B
A
B
C
D
3.小华拿27元钱购买圆珠笔和练习册,已知一本练习册2元,一支圆珠笔1元,他买了4本练习册,x支圆珠笔,则关于x的不等式表示正确的是( )
B
A.2×4+x<27 B.2×4+x≤27
C.2x+4≤27 D.2x+4≥27
4. 用不等式表示:
(1)c的4倍大于或等于8;
(2)c的一半小于或等于3;
(3)d与e的和不小于0;
(4)d与e的差不大于-2.
4c≥8
d+e≥0
d-e≤-2
c≤3
5. 利用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x+3>-1; (2)6x≤5x-7;
(3)- x< ; (4)4x≥-12.
x>-4
x≤-7
x>-2
x≥-3
6.用炸药爆破时,如果导火索燃烧的速度是 0.8 cm/s,人跑开的速度是每秒 4 m,为了使点导火索的战士在爆破时能够跑到100 m 以外(不含 100 m)的安全区域,这个导火索的长度应大于多少厘米?请将解集在数轴上表示出来.
解:设导火索的长度是 x cm,根据题意得:
×4>100,
解得:x>20.
答:导火索的长度应大于 20 cm.
在数轴上表示 x 的取值范围如图所示:
不等式性质的应用
1.利用不等式的性质解不等式.
2.不等式的实际应用:在利用不等式的性质解决实际问题时一定要注意未知数的实际意义.
课堂小结
再见
第2课时
第九章 不等式与不等式组
2021年春人教版七年级(下)数学
某长方体形状的容器长5cm,宽3cm,高10cm.容器内原有水的高度为3cm,现准备向它继续注水.用V(单位cm3)表示新注入水的体积,写出V的取值范围.
新课导入
(1)能运用不等式的性质对不等式进行变形和解简单的不等式.
(2)知道符号“≥”和“≤”的意义及在数轴上表示不等式的解集时实心点与空心圈的区别.
学习目标
利用不等式的性质解不等式
例1 利用不等式的性质解下列不等式:
(1)x-7>26;(2)3x<2x+1
(3) x>50 (4)-4x>3
探究新知
分析
解不等式,就是借助不等式的性质使不等式逐步化为 x>a 或 x
解这个不等式要利用哪个性质?
要利用不等式的性质1.
(1)x-7>26
根据不等式的性质1,不等式两边加7,不等号的方向不变,所以:
x-7+7>26+7
x>33
0
33
用数轴表示为
你能把不等式的解集用数轴表示出来吗?
(2)3x<2x+1
根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以:
3x-2x<2x+1-2x
x<1
用数轴表示为
0
1
(3) x>50
x>75
根据不等式的性质2,不等式两边乘 ,不等号的方向不变,所以:
× x> ×50
0
75
用数轴表示为
你能独自解不等式(4)吗?试一试.
(4)-4x>3
根据不等式的性质3,不等式两边除以 -4,不等号的方向改变,所以:
用数轴表示为
0
在表示两个数量大小关系时,我们会经常用到像 a≥b 或 a≤b 这样的式子,如一天内的温度变化 t≥19℃ 且 t≤28℃.
符号“≥”与“>”的意思有什么区别?
“≥”表示包含某个数值, “>” 表示不包含该数值.
“≤”表示包含某个数值, “<” 表示不包含该数值.
“≤”与“<”呢?
它们是否具有与前面所说的不等式的性质类似的性质呢?
它们也具有和不等式相同的性质.
如果a≥b,那么a±c≥b±c;
如果a≥b,那么 ac≥bc或 ≥ (其中c>0);
如果a≥b,那么ac≤bc或 ≤ (其中c<0).
归纳小结
1.用不等式的性质解下列不等式,并在数轴上表示出来.
(1)x+5>-1; (2)4x<3x-5;
(3) x< ; (4) -8x>10 .
针对练习
(1)x+5>-1; (2)4x<3x-5;
x>-6
0
-6
4x-3x<3x-5-3x
x+5-5>-1-5
x<-5
0
-5
(3) x< ; (4) -8x>10 .
7× x<7×
x<6
0
6
0
2.用不等式表示下列语句并写出解集,并在数轴上表示解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
3x≥1
x≥
0
x+3≥6
x≥3
0
3
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
y-1≤0
y≤1
0
1
y≤-8
y≤-2
0
-8
不等式的实际应用
某长方体形状的容器长5cm,宽3cm,高10cm.容器内原有水的高度为3cm,现准备向它继续注水.用V(单位cm3)表示新注入水的体积,写出 V 的取值范围.
学习了用不等式的性质解不等式,你现在能解决这个问题了吗?
探究新知
分析
要求新注入水的体积范围,那就要求出容器的总体积和已经被占用的体积.
容器的总体积为:
3×5×10
被占用的容器的体积为:
3×5×3
根据题意有:
V+3×5×3≤3×5×10
V+3×5×3≤3×5×10
V≤105
不是.在利用不等式解决实际问题时一定要考虑未知数的实际意义.
这样就可以了吗?
V+3×5×3≤3×5×10
V≥0且V≤105
考虑到实际意义,新注入水的体积 V 不能是负数,因此 V 的取值范围是:
V≤105
在数轴上表示出来为:
0
105
0
105
这里是实心圆表示,那实心圆与空心圆有什么区别呢?
实心圆表示不等式的取值范围包括这两个数,空心圆表示不等式的取值范围不包括这两个数.
1.解不等式的依据:不等式的性质.
2.在利用不等式的性质解决实际问题时一定要注意未知数的实际意义.
归纳小结
运用不等式的性质3时未改变不等号的方向
解不等式:2-3x>11.
错 解
不等式的两边同减2得-3x>9,
不等式的两边同除以-3得x>-3,
所以原不等式的解集为x>-3.
误区诊断
运用不等式的性质3时未改变不等号的方向
解不等式:2-3x>11.
不等式的两边同减2得-3x>9,
不等式的两边同除以-3得x<-3,
所以原不等式的解集为x<-3.
正 解
误区诊断
错因分析
此题错在没有理解不等式的性质3.在运用不等式的性质3时,不等式的两边乘(或除以)同一个负数,不等号的方向要改变.
1. 不等式3-2x≤7的解集是( )
A.x≥-2 B.x≤-2
C.x≤-5 D.x≥-5
A
课堂练习
2.不等式 x-2≥0 的解集在数轴上表示正确的是( )
B
A
B
C
D
3.小华拿27元钱购买圆珠笔和练习册,已知一本练习册2元,一支圆珠笔1元,他买了4本练习册,x支圆珠笔,则关于x的不等式表示正确的是( )
B
A.2×4+x<27 B.2×4+x≤27
C.2x+4≤27 D.2x+4≥27
4. 用不等式表示:
(1)c的4倍大于或等于8;
(2)c的一半小于或等于3;
(3)d与e的和不小于0;
(4)d与e的差不大于-2.
4c≥8
d+e≥0
d-e≤-2
c≤3
5. 利用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x+3>-1; (2)6x≤5x-7;
(3)- x< ; (4)4x≥-12.
x>-4
x≤-7
x>-2
x≥-3
6.用炸药爆破时,如果导火索燃烧的速度是 0.8 cm/s,人跑开的速度是每秒 4 m,为了使点导火索的战士在爆破时能够跑到100 m 以外(不含 100 m)的安全区域,这个导火索的长度应大于多少厘米?请将解集在数轴上表示出来.
解:设导火索的长度是 x cm,根据题意得:
×4>100,
解得:x>20.
答:导火索的长度应大于 20 cm.
在数轴上表示 x 的取值范围如图所示:
不等式性质的应用
1.利用不等式的性质解不等式.
2.不等式的实际应用:在利用不等式的性质解决实际问题时一定要注意未知数的实际意义.
课堂小结
再见
