1.4.3诱导公式与对称 课件(共21张PPT)——2020-2021学年高一下学期北师大版(2019)必修第二册第一章第四节
文档属性
| 名称 | 1.4.3诱导公式与对称 课件(共21张PPT)——2020-2021学年高一下学期北师大版(2019)必修第二册第一章第四节 |

|
|
| 格式 | pptx | ||
| 文件大小 | 644.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览







文档简介
诱导公式与对称
授课教师:
温故知新
学习目标
1. 利用单位圆的对称性推导诱导公式.
2. 掌握三角函数的诱导公式.(难点)
3. 能运用诱导公式化简简单的三角函数式及证明简单的三角恒等式.(重点)
课文精讲
在平面直角坐标系中,设任意角α和- α的终边与单位圆的交点分别为点P和P′,如图,不难看出,这两个角的终边OP,OP ′ 关于x轴对称.因此,点P和P′的横坐标相等,纵坐标的绝对值相等且符号相反.
角α与- α的正弦函数、余弦函数关系
课文精讲
即
角α与- α的正弦函数、余弦函数关系
sin(-α)=-sinα,所以正弦函数v= sinα是奇函数;
cos(-α) =cosα,所以余弦函数u=cosα是偶函数.
课文精讲
在平面直角坐标系中,设任意角α的终边与单位圆的交点为P,当点P沿逆(顺)时针方向旋转π弧度至点P′时,点P′就是α±π的终边与单位圆的交点(如图).
角α与 α±π的正弦函数、余弦函数关系
课文精讲
不难看出,点P'与点P关于原点对称.因此,它们的横坐标的绝对值相等且符号相反,纵坐标的绝对值也相等且符号相反.即
角α与 α±π的正弦函数、余弦函数关系
sin(α+π) =-sinα,cos(α-π)=-sinα.
cos(α+π) =-cosα,cos(α-π)=-cosα.
课文精讲
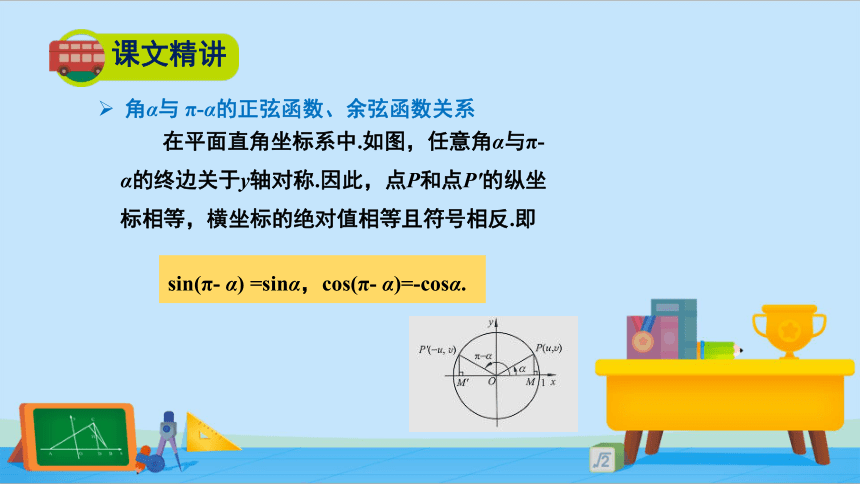
在平面直角坐标系中.如图,任意角α与π- α的终边关于y轴对称.因此,点P和点P′的纵坐标相等,横坐标的绝对值相等且符号相反.即
角α与 π-α的正弦函数、余弦函数关系
sin(π- α) =sinα,cos(π- α)=-cosα.
课文精讲
sin(π- α) =sinα,cos(π- α)=-cosα.
角α与 π-α的正弦函数、余弦函数关系
这两个公式也可以由前两组公式推出:
sin(π- α)=-sin(α-π)=-(-sinα)= sinα,
cos(π- α)=cos(α-π)=-cosα.
课文精讲
记忆口诀:“函数名不变,符号看象限”.
角α与 π-α的正弦函数、余弦函数关系
“函数名不变”是指等式两边的三角函数同名;
“符号看象限”是指把原角看成锐角时新角在原函数下的符号,由新角所在象限确定符号,如sin(α+π) ,若把α看成锐角,则α+π在第三象限,所以取负值,故sin(α+π)=-sinα.
课文精讲
你能归纳一下把任意角的三角函数转化为锐角三角函数的步骤吗?
角α与 π-α的正弦函数、余弦函数关系
利用诱导公式可把任意角的三角函数转化为锐角三角函数,口诀是“负化正,大化小,化到锐角再查表”.
典型例题
例1:借助下列各组中两个角的终边与单位圆的交点,说出它们的对称关系.
(1) 与 ;(2) 与 ;
?????????
?
????????????
?
??????????????????
?
????????
?
(3) 与 ;(4) 与 .
解: (1)如图, 与 的终边与
单位圆的交点关于原点
对称;
????????????
?
????????
?
????????????
?
????????
?
?????????
?
-?????????????????
?
典型例题
例1:借助下列各组中两个角的终边与单位圆的交点,说出它们的对称关系.
(1) 与 ;(2) 与 ;
?????????
?
?????????????
?
?????????????
?
????????
?
??????????????????
?
????????
?
(3) 与 ;(4) 与 .
解: (2)如图, 与 的终边与
单位圆的交点关于y轴对
称;
????????????
?
????????
?
?????????
?
-?????????????????
?
典型例题
例1:借助下列各组中两个角的终边与单位圆的交点,说出它们的对称关系.
(1) 与 ;(2) 与 ;
?????????
?
?????????????
?
?????????????
?
????????
?
??????????????????
?
????????
?
(3) 与 ;(4) 与 .
解: (3)如图, 与 的终边与
单位圆的交点关于x轴对
称;
?????????????????
?
????????
?
?????????
?
-?????????????????
?
典型例题
例1:借助下列各组中两个角的终边与单位圆的交点,说出它们的对称关系.
(1) 与 ;(2) 与 ;
?????????
?
?????????????
?
?????????????
?
????????
?
??????????????????
?
????????
?
(3) 与 ;(4) 与 .
解: (4)如图, 与 的终边与
单位圆的交点关于y轴对
称.
????????
?
-?????????????????
?
?????????
?
-?????????????????
?
典型例题
例2:求下列三角函数值:
(1) ;(2) ;
(3) ; (4)
解: (1)
sin ???????????????
?
cos??????????????
?
sin??????????????????
?
cos ???????????????????.
?
sin ???????????????=- sin??????????????
= sin ????+??????????=sin??????????=?????????? ;
?
(2)
cos??????????????= cos ???????????+????
=-cos ???????????=- cos ??????????=-???????? ;
?
典型例题
例2:求下列三角函数值:
(1) ;(2) ;
(3) ; (4)
解: (3)
sin ???????????????
?
cos??????????????
?
sin??????????????????
?
cos ???????????????????.
?
sin ???????????????????=sin ???????????+????????
= sin ???????????=-sin??????????=-????????? ;
?
(4)
cos ???????????????????=cos?????????????????? =cos ??????????????+????????
?
=cos??????????????=cos ??????????+????=-cos??????????=-?????????.
?
综合练习
估计sin2020°的大小属于区间( )
A. ?????,???????? B. ?????????,????
C. ????,???????? D. ????????,????
?
解:∵sin2020°=sin(360°×6-140°)=?sin140°=?sin40°,
∵sin40°∈( ,1),
∴sin2020°=?sin40°∈(-1,?????????).
故选:A.
?
????????
?
A
综合练习
比较大小:cos ????????????????????? ____ cos ?????????????????.
?
解: cos ????????????????????? = cos ??????????????????????????
=cos ????????????????? = cos????????????????,
cos ?????????????????= cos ??????????????????????
= cos????????????,
∵y=cosx在(0,π)上为减函数,
∴cos????????????????> cos????????????,
即cos ????????????????????? > cos ?????????????????.
?
>
本课小结
再 见
授课教师:
温故知新
学习目标
1. 利用单位圆的对称性推导诱导公式.
2. 掌握三角函数的诱导公式.(难点)
3. 能运用诱导公式化简简单的三角函数式及证明简单的三角恒等式.(重点)
课文精讲
在平面直角坐标系中,设任意角α和- α的终边与单位圆的交点分别为点P和P′,如图,不难看出,这两个角的终边OP,OP ′ 关于x轴对称.因此,点P和P′的横坐标相等,纵坐标的绝对值相等且符号相反.
角α与- α的正弦函数、余弦函数关系
课文精讲
即
角α与- α的正弦函数、余弦函数关系
sin(-α)=-sinα,所以正弦函数v= sinα是奇函数;
cos(-α) =cosα,所以余弦函数u=cosα是偶函数.
课文精讲
在平面直角坐标系中,设任意角α的终边与单位圆的交点为P,当点P沿逆(顺)时针方向旋转π弧度至点P′时,点P′就是α±π的终边与单位圆的交点(如图).
角α与 α±π的正弦函数、余弦函数关系
课文精讲
不难看出,点P'与点P关于原点对称.因此,它们的横坐标的绝对值相等且符号相反,纵坐标的绝对值也相等且符号相反.即
角α与 α±π的正弦函数、余弦函数关系
sin(α+π) =-sinα,cos(α-π)=-sinα.
cos(α+π) =-cosα,cos(α-π)=-cosα.
课文精讲
在平面直角坐标系中.如图,任意角α与π- α的终边关于y轴对称.因此,点P和点P′的纵坐标相等,横坐标的绝对值相等且符号相反.即
角α与 π-α的正弦函数、余弦函数关系
sin(π- α) =sinα,cos(π- α)=-cosα.
课文精讲
sin(π- α) =sinα,cos(π- α)=-cosα.
角α与 π-α的正弦函数、余弦函数关系
这两个公式也可以由前两组公式推出:
sin(π- α)=-sin(α-π)=-(-sinα)= sinα,
cos(π- α)=cos(α-π)=-cosα.
课文精讲
记忆口诀:“函数名不变,符号看象限”.
角α与 π-α的正弦函数、余弦函数关系
“函数名不变”是指等式两边的三角函数同名;
“符号看象限”是指把原角看成锐角时新角在原函数下的符号,由新角所在象限确定符号,如sin(α+π) ,若把α看成锐角,则α+π在第三象限,所以取负值,故sin(α+π)=-sinα.
课文精讲
你能归纳一下把任意角的三角函数转化为锐角三角函数的步骤吗?
角α与 π-α的正弦函数、余弦函数关系
利用诱导公式可把任意角的三角函数转化为锐角三角函数,口诀是“负化正,大化小,化到锐角再查表”.
典型例题
例1:借助下列各组中两个角的终边与单位圆的交点,说出它们的对称关系.
(1) 与 ;(2) 与 ;
?????????
?
????????????
?
??????????????????
?
????????
?
(3) 与 ;(4) 与 .
解: (1)如图, 与 的终边与
单位圆的交点关于原点
对称;
????????????
?
????????
?
????????????
?
????????
?
?????????
?
-?????????????????
?
典型例题
例1:借助下列各组中两个角的终边与单位圆的交点,说出它们的对称关系.
(1) 与 ;(2) 与 ;
?????????
?
?????????????
?
?????????????
?
????????
?
??????????????????
?
????????
?
(3) 与 ;(4) 与 .
解: (2)如图, 与 的终边与
单位圆的交点关于y轴对
称;
????????????
?
????????
?
?????????
?
-?????????????????
?
典型例题
例1:借助下列各组中两个角的终边与单位圆的交点,说出它们的对称关系.
(1) 与 ;(2) 与 ;
?????????
?
?????????????
?
?????????????
?
????????
?
??????????????????
?
????????
?
(3) 与 ;(4) 与 .
解: (3)如图, 与 的终边与
单位圆的交点关于x轴对
称;
?????????????????
?
????????
?
?????????
?
-?????????????????
?
典型例题
例1:借助下列各组中两个角的终边与单位圆的交点,说出它们的对称关系.
(1) 与 ;(2) 与 ;
?????????
?
?????????????
?
?????????????
?
????????
?
??????????????????
?
????????
?
(3) 与 ;(4) 与 .
解: (4)如图, 与 的终边与
单位圆的交点关于y轴对
称.
????????
?
-?????????????????
?
?????????
?
-?????????????????
?
典型例题
例2:求下列三角函数值:
(1) ;(2) ;
(3) ; (4)
解: (1)
sin ???????????????
?
cos??????????????
?
sin??????????????????
?
cos ???????????????????.
?
sin ???????????????=- sin??????????????
= sin ????+??????????=sin??????????=?????????? ;
?
(2)
cos??????????????= cos ???????????+????
=-cos ???????????=- cos ??????????=-???????? ;
?
典型例题
例2:求下列三角函数值:
(1) ;(2) ;
(3) ; (4)
解: (3)
sin ???????????????
?
cos??????????????
?
sin??????????????????
?
cos ???????????????????.
?
sin ???????????????????=sin ???????????+????????
= sin ???????????=-sin??????????=-????????? ;
?
(4)
cos ???????????????????=cos?????????????????? =cos ??????????????+????????
?
=cos??????????????=cos ??????????+????=-cos??????????=-?????????.
?
综合练习
估计sin2020°的大小属于区间( )
A. ?????,???????? B. ?????????,????
C. ????,???????? D. ????????,????
?
解:∵sin2020°=sin(360°×6-140°)=?sin140°=?sin40°,
∵sin40°∈( ,1),
∴sin2020°=?sin40°∈(-1,?????????).
故选:A.
?
????????
?
A
综合练习
比较大小:cos ????????????????????? ____ cos ?????????????????.
?
解: cos ????????????????????? = cos ??????????????????????????
=cos ????????????????? = cos????????????????,
cos ?????????????????= cos ??????????????????????
= cos????????????,
∵y=cosx在(0,π)上为减函数,
∴cos????????????????> cos????????????,
即cos ????????????????????? > cos ?????????????????.
?
>
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
